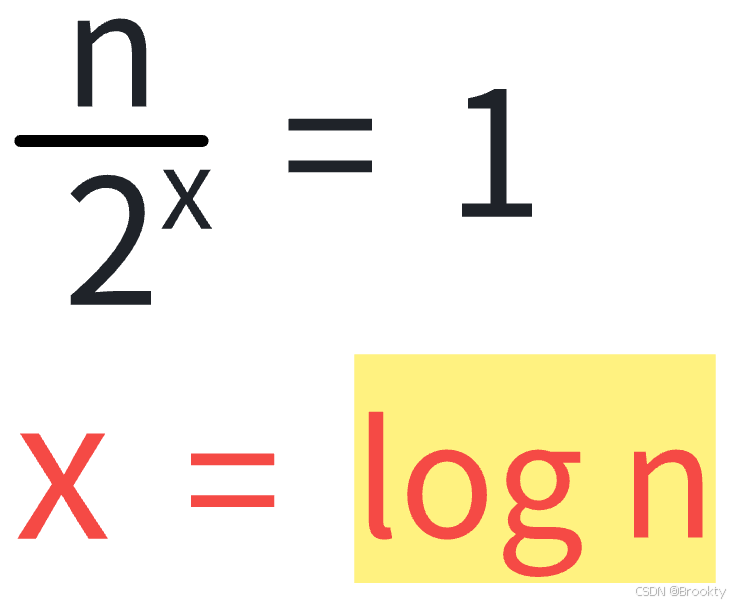【算法】二分查找(一)朴素二分

目录

一、题目介绍

二、朴素二分

1.原理

二段性

时间复杂度(logn](https://blog.csdn.net/2401_86112610/article/details/152011659?spm=1011.2124.3001.6209 ")")

2.模板

四、提交代码

---

一、题目介绍

704. 二分查找 - 力扣（LeetCode）

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果 target 存在返回下标，否则返回 -1。

你必须编写一个具有 O(log n) 时间复杂度的算法。

示例 1:

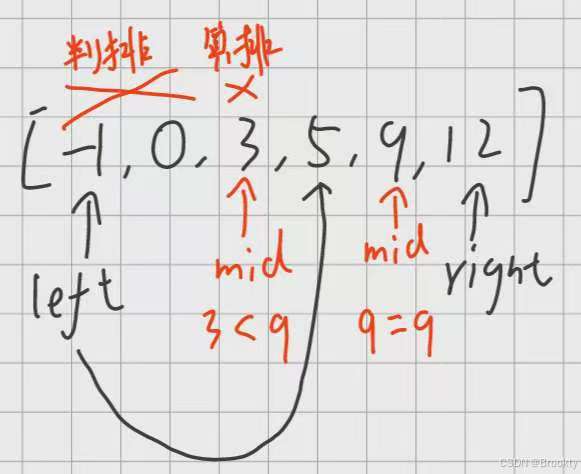
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

---

二、朴素二分

1.原理

二段性

二段性 一次算可排一边 每次在中间 固定算排二分之一

• 暴力 是 纯用算来排 ，一次算 就只排 了 此个
• 优化 是 增有判来排 ，一次算 有额外 排 多个

时间复杂度(logn)

算x次剩 个未算排 最差直到最后剩1个后算排完

---

2.模板

int left = 0, right = nums.length - 1;

while(left <= right)

int mid = left + (right + left) / 2;

if(二段性排掉左边) left = mid + 1;

else if(二段性排掉右边) right = mid - 1;

else return;

}

---

四、提交代码

public int search(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while(left <= right) {
        //int mid = (left + right) / 2; 如果两个大数相加 就会和溢出算数范围，所以相加时得一方是确保小数
        int mid = left + (right - left) / 2; // 一方小数求中点(算术和为mid 比right小 都没有溢出)
        if(nums[mid] > target) right = mid - 1;
        else if(nums[mid] < target) left = mid + 1;
        else return mid;
    }
    return -1;
}