在漫长的数学历史长河当中,诞生了无数美丽的数学公式,它们宛如一颗颗璀璨的明珠,光彩夺目,而只有它被称为上帝公式,它就是欧拉公式。

那我们来看一下它有什么特别之处啊,它的形式是这样的,E 的 ix 次方等于 cos x 加上 I 乘以sinx ,其中 E 是自然常数,I 是虚数,sin , cos 呢是三角函数。
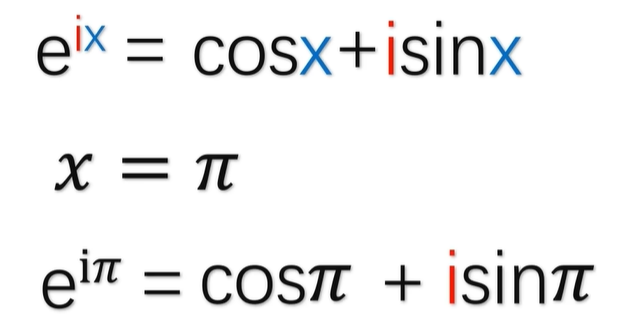
当 X 等于π的时候啊,公式就变成了 E 的iπ次方等于-1,这个就是欧拉恒等式。
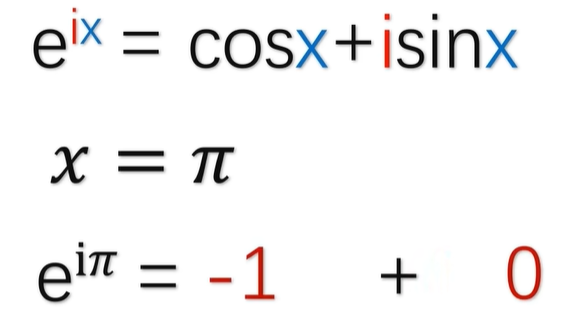 ,
,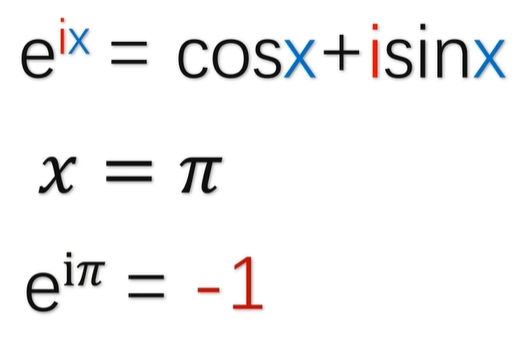
这个等式包含了自然常数、虚数、圆周率和自然数,每一个单拿出来啊,在数学史上都是非常炸裂的存在,而欧拉公式竟然以一种极其简洁的形式,轻描淡写般把它们结合了在一起,在以简洁为美的数学世界里啊,难怪他会被称为上帝公式啊。
事实上,与欧拉公式相近的公式,在此之前就已经被发现了啊,其实这也不奇怪,虚数的讲解中也有推导到类似的结果啊。
例如,1707年,法国数学家棣莫弗,就发现了一个这样的公式:

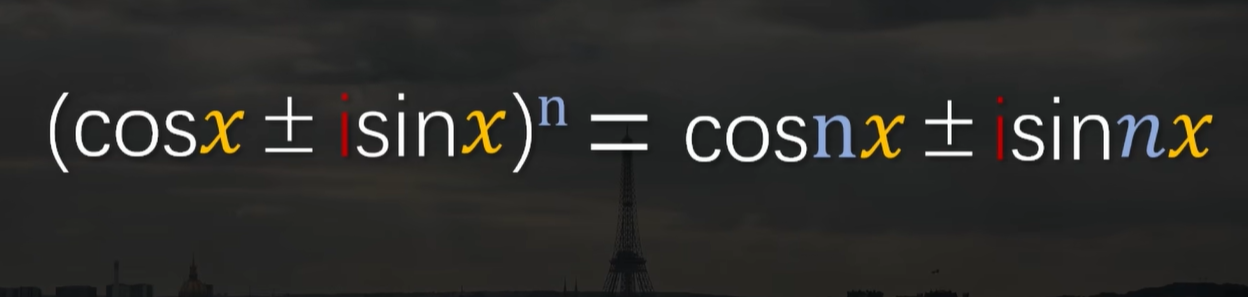
又例如1712年,英国数学家罗杰·科特斯,在研究螺旋线弧长的时候呢,

就得出了一个这样的公式:

这里注意一下啊,ln这个符号呢,是后来欧拉取的啊,是表示自然对数的意思。
在此之前,数学家们呢,都是用别的方法去表示自然对数的啊,这里我为了大家好理解,直接就用了ln。
包括虚数 i 也是后来欧拉给的符号,在此之前呢,虚数都被写作根号-1,我为了方便表达啊,也是直接用了 i。
这个公式呢,可以说是无限接近欧拉公式了,只要两边同时取 E 为底的指数操作就可以了。

不过,科特斯在1716年突然离世,这一结果呢,也从未正式发表过。
接下来,为了说明欧拉公式,我得先讲一下这个自然常数是什么啊。
自然常数e,其实我们在高中的时候呢,就接触过了,他和π一样,也是一个无理数来的,它约等于2.71828。

自然常数又被称为欧拉数,但是欧拉数却不是欧拉发现的。

是雅各布·伯努利,在研究存款复利的时候发现的。

注意一下,这里的伯努利和流体力学的伯努利啊,不是一个,流体力学的是丹尼尔·伯努利啊,他是雅各布的侄子。
这里说明e啊。其实是有两个数学模型可以选的:

一个呢,是一年之内无穷次存取计息啊,伯努利用的就是这个;
第二个呢,就是定期只存取一次啊,但是你可以存无穷多年,不过不同年份的定期啊,就会对应到不同的利率;
因为时间无穷细,这个事情对我来说呢,有点离谱啊,所以我这里用的就是第二个模型------假如银行规定了一个这样的规则,存一年利率就是100%,存两年利率就变成了50%,也就是1/2,存3年利率变为1/3,而存 N 年呢,利率就变成 N 分之一。

复利的意思就是今年的本加息呢,会变成下一年的本啊。

好,那么我们用一个具体的例子来说明啊,我有一块钱,存一年之后,到手就是1+1乘以百分百等于二,存两年,最后到手呢,就是1+2分之一,加上1+2分之1,再乘以1/2的,也就是1+2分之一的二次方等于2.25。

存3年,最后到手的就是1+3分之一的三次方,等于2.37的,以此类推啊,存 N 年一,最后呢,到时候就是一加上 N 分之一的 N 次方。
诶,这个时候我好像发现存的越久,赚的就越多,如果我存无穷多年,那么本息会不会最后就是无穷多呢???
不会,它只会无限趋向于2.71828......,甚至呢,都到不了2.72。
我们可以画一个 (1+1/x)^x 的函数图像啊,可以明显看到函数值到了2.71左右啊,就上不去了.
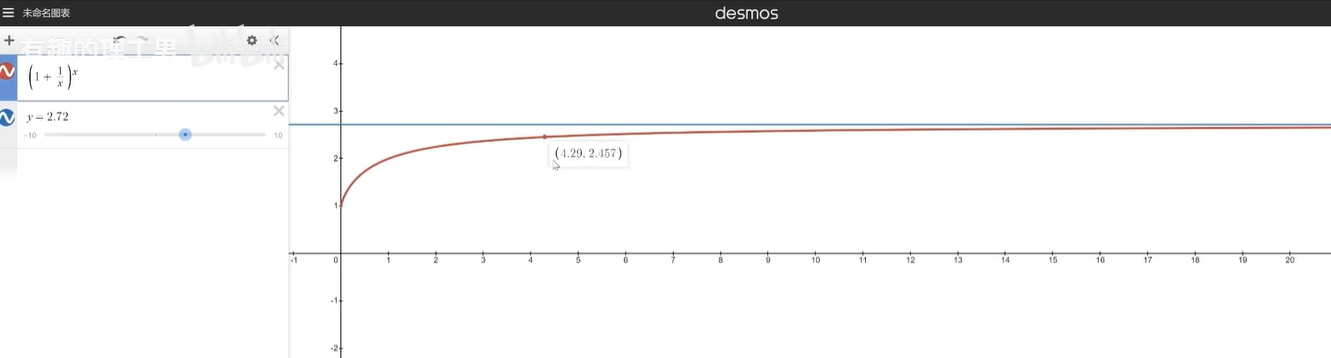
欧拉在他后来的著作中,多次引用到了这个数,并且给了他一个符号------e,所以这个数也被后人叫做欧拉数了。

这个自然常数有什么特别的地方呢,啊,我们来看一下啊,假如有一个指数函数是以e为底的,也就是 Y 等于 E 的 X 次方,我们随便找一个点吧,例如 X 等于二,那它的函数值呢,就是e的平方,在这一个点的导数,也就是切线的斜率,它也是e的平方,函数曲线与 X 轴围成的面积呢,它也还是e的平方。
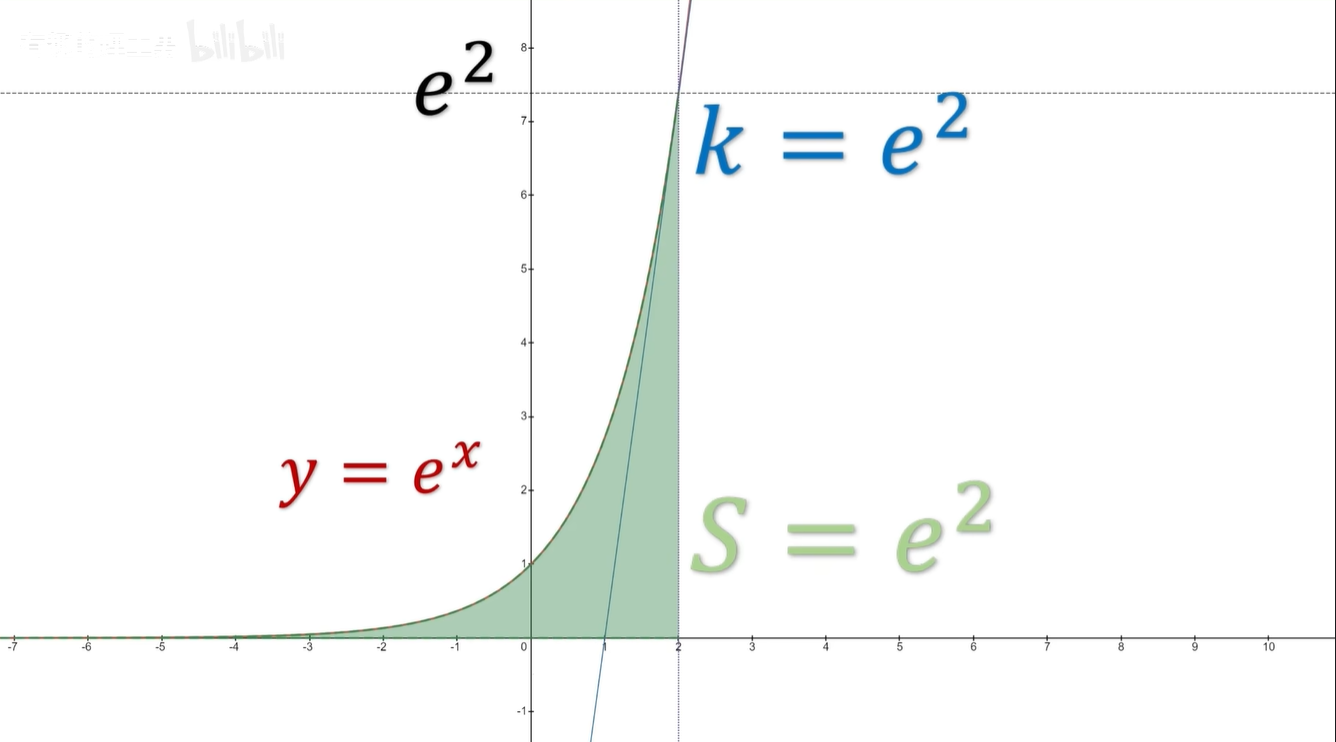
放眼整个数学界,这个函数的特性啊,也是独一份的啊。
当然,三角函数 sin x 啊,求两次导之后呢,会变成自己的相反数啊,这个特性倒是和 E 的 X 次方啊,有点类似,感觉这两个函数冥冥之中就是有关联的。
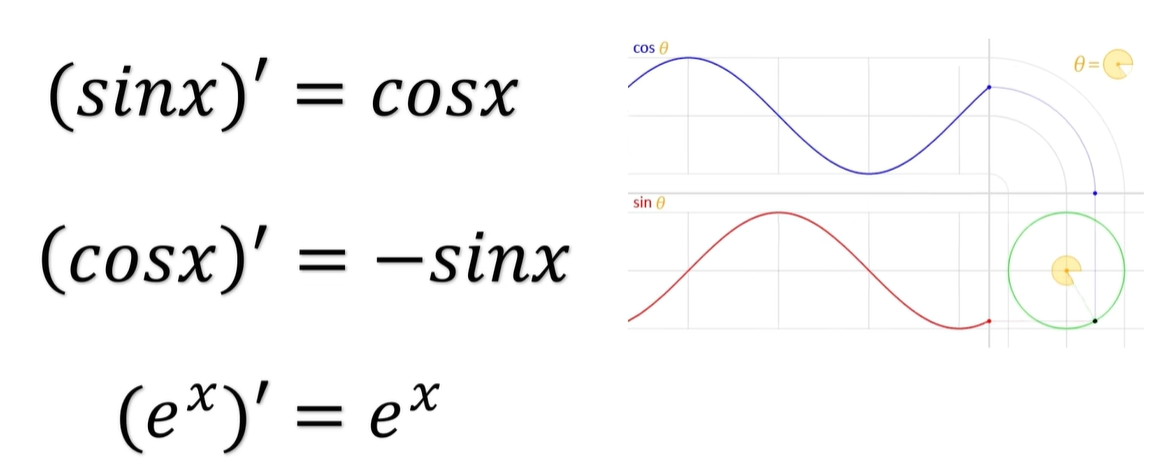
当然,对复数领域和三角函数领域,研究颇深的欧拉也是这样认为的。
1748年,欧拉发表了一篇名为无限研究导论的论文,里面就引用了棣莫弗的公式啊。
我们来看一下啊,两式相加除以二,就得到了 cos 的 NX ,两式相减除以2i,就得到了 sin 的 NX 。
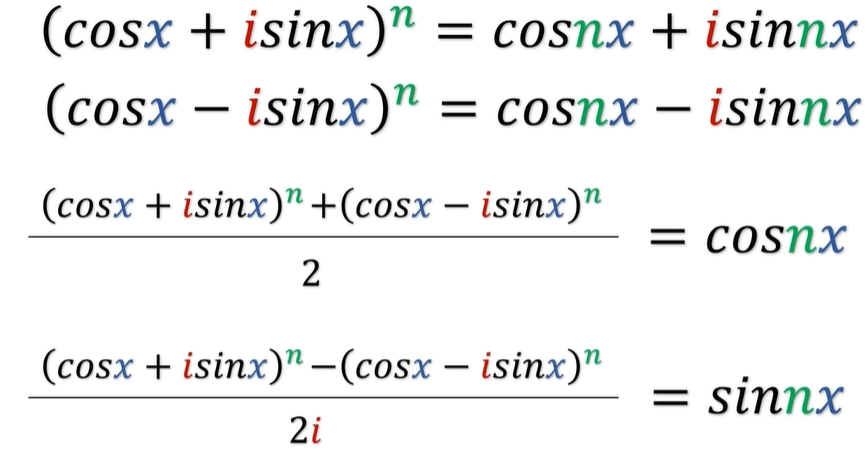 ,
,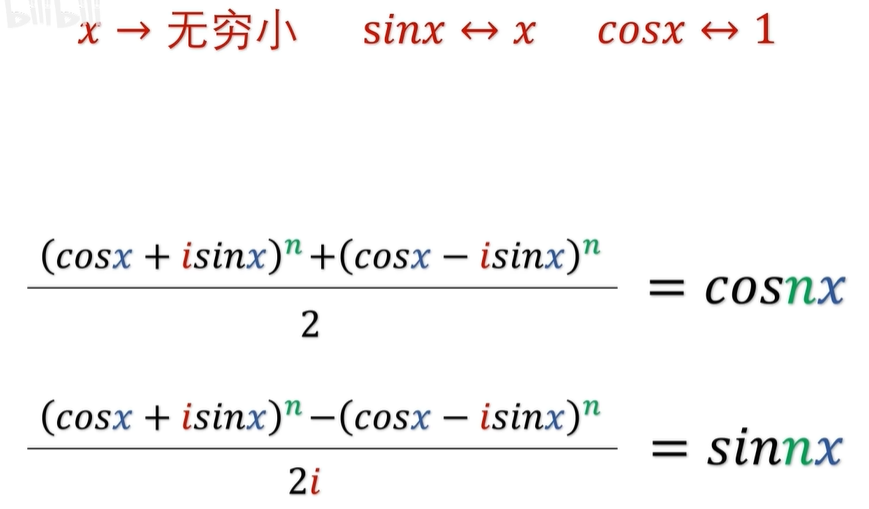
欧拉大胆地把 X 取了无穷小,于是呢,就有了 sin x 是等价于x的,cos x 呢是等价于1的啊。

那么式子呢,就变成了这样。
然后再取 N 为无穷大,令到 nx 等于 K 啊,那么就有 X 呢,是等于 K 除以 N 的,最终的式子呢,又变成了这样。
 ,
,
诶,大家看,这不就是我们刚刚讲过复利的计算形式吗。
加号坐边其实是E 的ik次方,而这个呢,就是 E 的-ik次方,所以最后cosk和 sink呢,就变成了这样。
 ,
,
哎,我们看这两个式子,拿二式乘以 I 再加上一式,于是乎我们就得到了,欧拉公式的最终形式。
之前讲虚数的时候就有提到过,cosx+isinx可以在复平面上表示旋转,所以呢, E 的 IK 次方也是一样的。
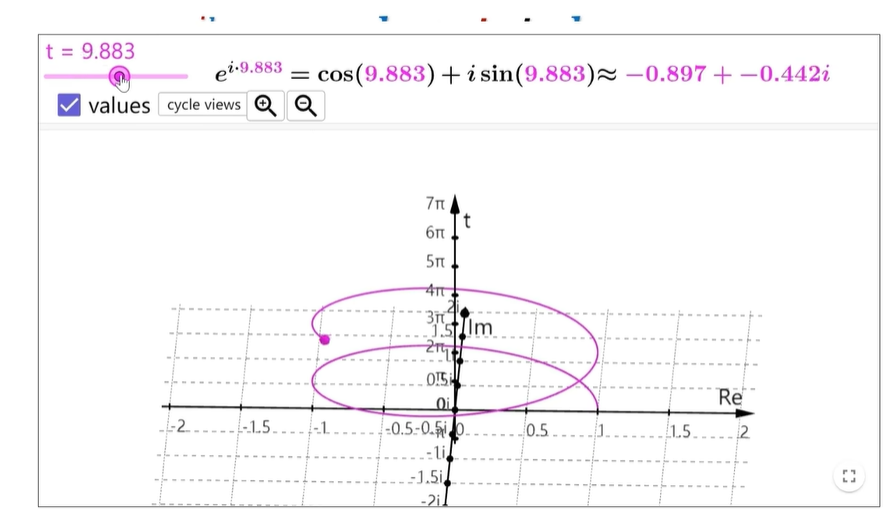
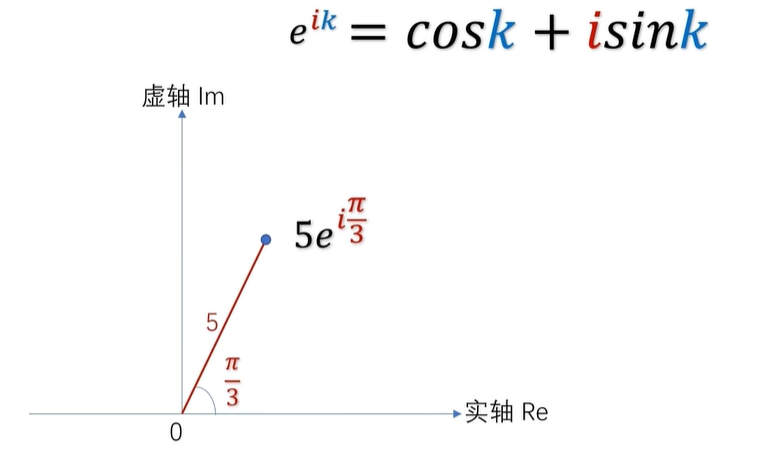
举个例子,5×e的iπ/3次方,这个数表示了复平面上五为半径,逆时针旋转了60度所在的位置啊。
又例如一个复数,1+i化成复指数,形式是怎样的呢?
在复平面上画出来一加 I 的点在这,它的半径就是根号二,旋过的角度刚刚好是45度,也就是四分之派。

用三角函数表示呢,就是根号二乘以 cosπ/4,加上 I 乘以 sinπ/4,也就是根号2×e^iπ/4。
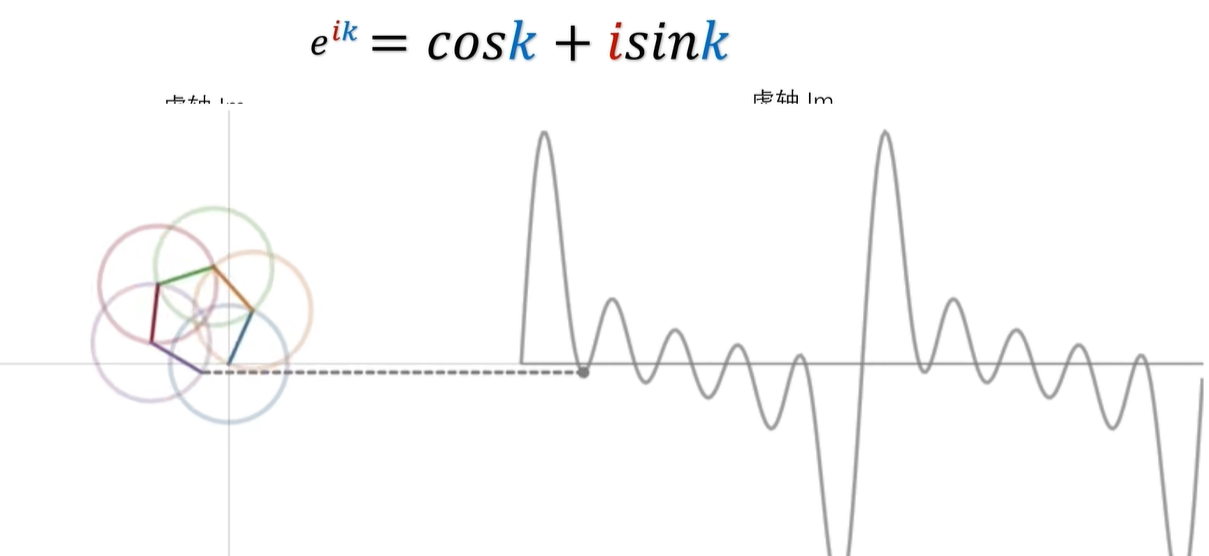
好,至此,欧拉公式就跟三角函数和旋转,关联了到一起了。
你想想啊,傅里叶级数还得用 sin 和 cos 两种函数,做基底去分解,如果用e^iθ去做基底的话呢,一个就够了。
【结论】
- 傅里叶变换(级数)的三角形式到复指数形式的转变;c + s → e^iωt
- 傅里叶变换到拉普拉斯变换的转变;σ + iω = s
都有的重要的动因:
- 书写量更少;
- 运算规则更简单;