
小波变换(Wavelet Transform)作为一种重要的时频分析工具,克服了傅里叶变换在处理非平稳信号时的局限性。小波变换通过引入可伸缩和平移的基函数,实现了对信号时频结构的自适应刻画,拥有FFT、STFT没有的性能。
关键词:小波变换;时频分析;傅里叶变换;多分辨率分析;信号处理
文章目录
引言
随着信号处理技术的不断发展,对非平稳信号的分析需求日益增加。传统的傅里叶变换虽能有效提取信号的频域特征,但无法刻画频率成分随时间变化的情况。短时傅里叶变换(STFT)通过加窗方式引入时域局部性,但其固定窗口限制了时频分辨率的灵活性。
傅里叶变换的局限性
傅里叶变换将信号分解为不同频率的正弦波与余弦波的叠加,适用于平稳信号分析。然而,对于频率随时间变化的非平稳信号(如生物医学信号、振动信号等),傅里叶变换仅能提供全局频谱信息,无法反映频率成分的时域分布。
数学表达 :
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt F(ω)=∫−∞∞f(t)e−jωtdt
该变换丢失了时间维度信息,导致时域差异大的信号可能具有相同的频谱。
短时傅里叶变换(STFT)及其不足
STFT通过添加滑动时间窗,对局部信号段进行傅里叶变换,从而得到时频联合分布:
S T F T ( t , ω ) = ∫ − ∞ ∞ f ( τ ) w ( τ − t ) e − j ω τ d τ STFT(t, \omega) = \int_{-\infty}^{\infty} f(\tau) w(\tau - t) e^{-j\omega \tau} d\tau STFT(t,ω)=∫−∞∞f(τ)w(τ−t)e−jωτdτ
其中 w ( t ) w(t) w(t)为窗函数(如汉明窗)。
缺陷:窗函数宽度固定,导致时间分辨率与频率分辨率之间存在权衡(海森堡不确定性原理)。窄窗时间分辨率高但频率分辨率低,宽窗则相反,难以适应非平稳信号中高频与低频成分的不同需求。
小波变换的基本原理
小波基函数
小波变换采用有限长、衰减的基函数(小波)替代傅里叶变换中的无限长三角函数。常用小波包括 Haar、Daubechies、Morlet 等。
小波函数通过尺度因子 a a a和平移因子 b b b进行伸缩与平移:
ψ a , b ( t ) = 1 a ψ ( t − b a ) \psi_{a,b}(t) = \frac{1}{\sqrt{a}} \psi\left(\frac{t - b}{a}\right) ψa,b(t)=a 1ψ(at−b)
其中 a a a控制频率(尺度), b b b控制时间位置。
连续小波变换(CWT)
连续小波变换定义为信号与小波基的内积:
C W T ( a , b ) = ∫ − ∞ ∞ f ( t ) ψ a , b ∗ ( t ) d t CWT(a, b) = \int_{-\infty}^{\infty} f(t) \psi_{a,b}^*(t) dt CWT(a,b)=∫−∞∞f(t)ψa,b∗(t)dt
通过调整 a a a和 b b b,可得到信号在不同尺度和时间上的能量分布,形成时频谱。
离散小波变换(DWT)与多分辨率分析
DWT通过二进伸缩与平移 a = 2 j , b = k ⋅ 2 j a = 2^j, b = k \cdot 2^j a=2j,b=k⋅2j实现高效计算。多分辨率分析(MRA)将信号分解为不同频带的近似与细节分量,适用于数据压缩、去噪和特征提取。
MATLAB示例
傅里叶变换,对时间维度的信息保留欠佳:
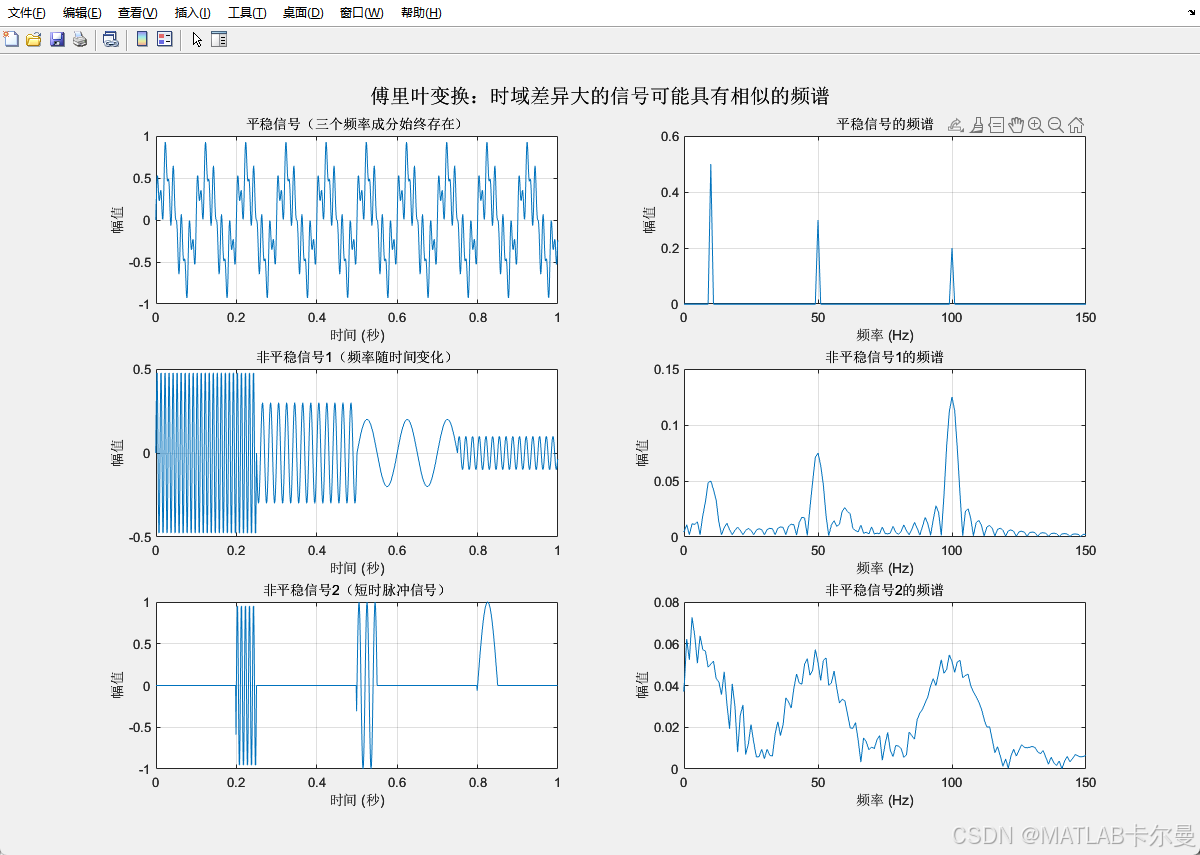
FFT与SWT对比:
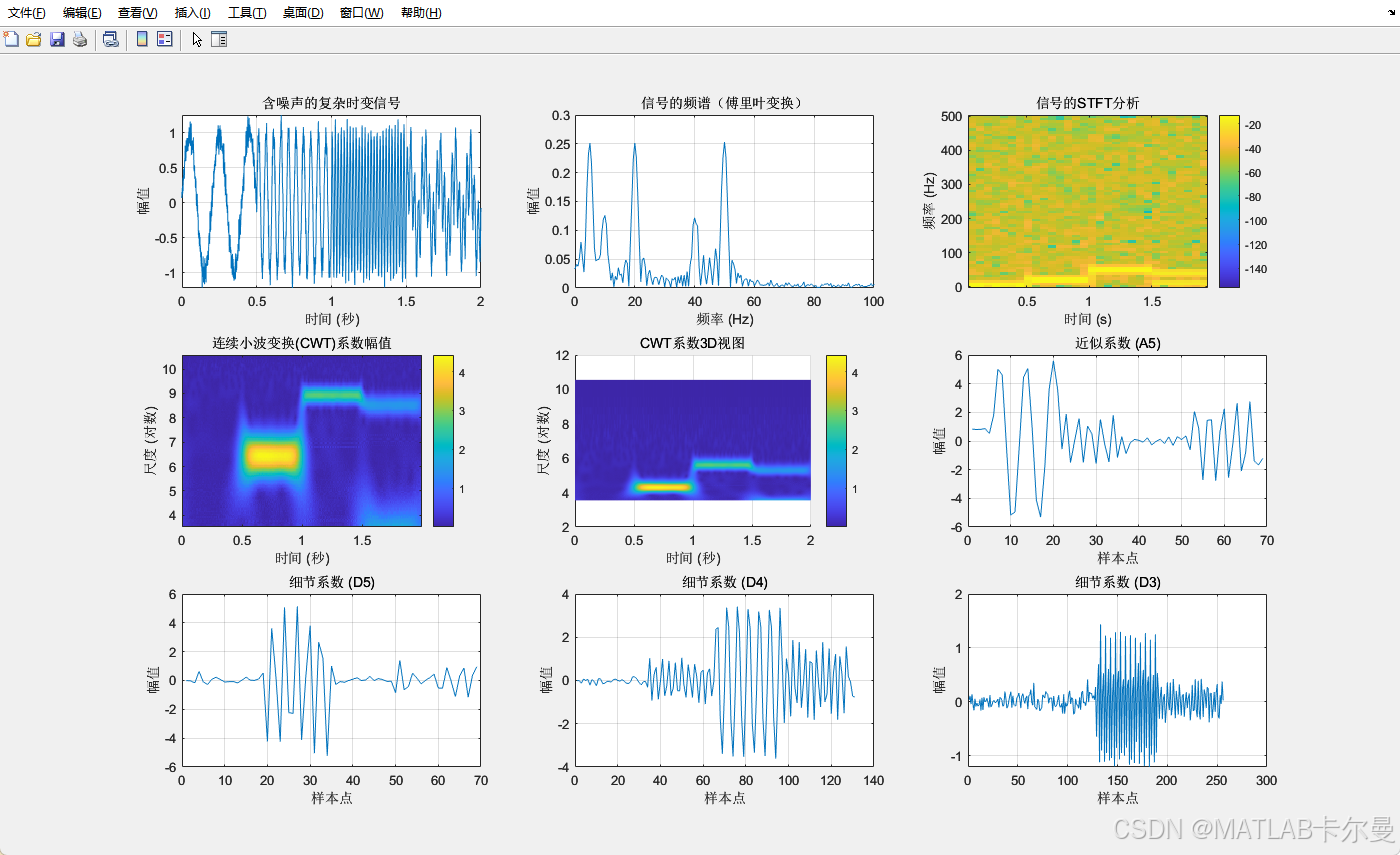
小波变换的优势
- 自适应时频分辨率:高频成分采用窄窗,低频成分采用宽窗,适应非平稳信号特性。
- 局部化能力:可精确检测信号的奇异点与突变。
- 正交性与稀疏性:正交小波基减少冗余,利于数据压缩与重构。
- 灵活性:可根据任务选择不同的小波基函数。
应用领域
- 信号处理:心电/脑电信号分析、故障诊断
- 图像处理:图像压缩、边缘检测、去噪
- 通信系统:信道均衡、调制识别
- 金融时间序列分析:特征提取等
结论与展望
小波变换通过时频局部化能力,为非线性、非平稳信号分析提供了有力工具。未来研究方向包括:
- 自适应小波基的优化选择;
- 小波与深度学习结合(如小波神经网络);
- 高维小波理论(如三维信号处理)。
小波变换的理论完善与应用拓展,将持续推动信号处理、医学成像、人工智能等领域的发展。
文中示例代码获取,可联系作者。