SciPy傅里叶变换与信号处理教程：数学原理与Python实现

SciPy傅里叶变换与信号处理教程：数学原理与Python实现

傅里叶变换（Fourier Transform）是信号处理、科学计算和数据分析中最为核心的数学工具之一。它通过将信号从时域 （time domain）转换至频域（frequency domain），揭示出信号内部所包含的周期成分和频率特征。在实际工程中，无论是语音信号处理、图像分析，还是物理实验数据的频谱分析，傅里叶变换都是理解与操作信号的关键手段。

本文将系统介绍傅里叶变换的基本概念与数学原理，并结合 SciPy 库展示其在 Python 中的具体实现。内容涵盖离散傅里叶变换（DFT）及快速算法 FFT、窗函数抑制频谱泄漏、实值序列优化方法（rFFT 与 irFFT）、二维信号处理（2D-FFT），以及离散余弦变换（DCT）在信号压缩中的应用。文中所有可视化均采用 Seaborn 风格进行美化，以增强图形的可读性与展示效果。

---

1. 从时域到频域：傅里叶变换的基本思想

我们常见的时域信号 x(t)x(t)x(t) 往往包含不同频率的周期分量。傅里叶变换的核心思想是：任意复杂的信号都可以分解为一系列正弦波与余弦波的叠加。其数学定义为
X(f)=∫−∞+∞x(t)e−j2πftdt X(f) = \int_{-\infty}^{+\infty} x(t) e^{-j 2 \pi f t} dt X(f)=∫−∞+∞x(t)e−j2πftdt

而逆变换为：
x(t)=∫−∞+∞X(f)ej2πftdf x(t) = \int_{-\infty}^{+\infty} X(f) e^{j 2 \pi f t} df x(t)=∫−∞+∞X(f)ej2πftdf

在实际计算机环境中，我们处理的多为离散信号。此时应使用 离散傅里叶变换（DFT） 或其高效实现形式------快速傅里叶变换（FFT）。这两者是理解数字信号频谱特征的基础。

---

2. 离散傅里叶变换（DFT）与快速傅里叶变换（FFT）

离散信号 x[n]x[n]x[n]，长度为 NNN，其傅里叶变换可表示为：
X[k]=∑n=0N−1x[n]e−i2πNkn,k=0,1,...,N−1 X[k] = \sum_{n=0}^{N-1} x[n] e^{-i \frac{2\pi}{N} k n}, \quad k=0,1,\dots,N-1 X[k]=n=0∑N−1x[n]e−iN2πkn,k=0,1,...,N−1

逆变换则为：
x[n]=1N∑k=0N−1X[k]ei2πNkn x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{i \frac{2\pi}{N} k n} x[n]=N1k=0∑N−1X[k]eiN2πkn

下面通过 Python 实例展示 FFT 的时域与频域表现。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.fft import fft
sns.set_theme(style="whitegrid", font="SimHei", rc={"axes.unicode_minus": False})

# 生成信号
fs = 150
t = np.arange(0, 1.0, 1/fs)
x = np.sin(np.pi*50*t) + 0.5*np.sin(np.pi*120*t)

# FFT
X = fft(x)
freqs = np.fft.fftfreq(len(t), 1/fs)

# 时域信号
plt.figure(figsize=(12,4))
sns.lineplot(x=t, y=x, color="dodgerblue", linewidth=2)
plt.title("时域信号", fontsize=16)
plt.xlabel("时间 (s)")
plt.ylabel("幅值")
plt.show()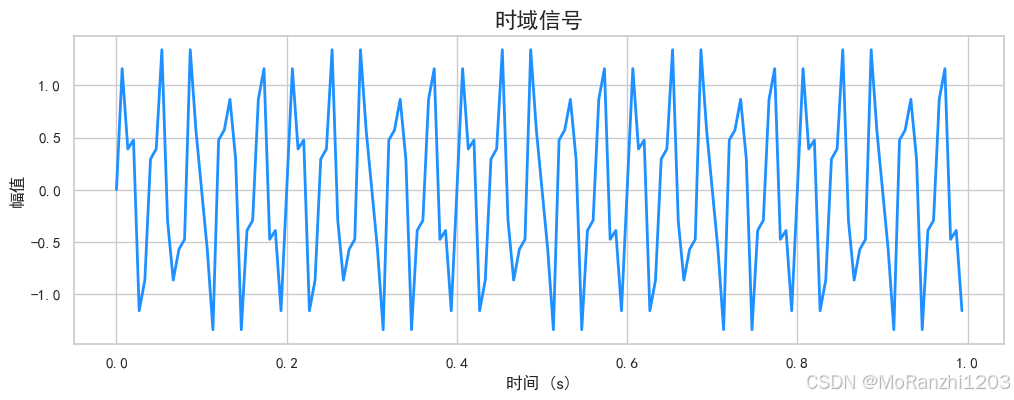

上图展示了时域下的复合正弦信号。我们可以进一步通过频谱图观察各频率分量的能量分布：

# 频域信号幅值
plt.figure(figsize=(12,4))
sns.lineplot(x=freqs[:len(freqs)//2], y=2/len(t)*np.abs(X[:len(X)//2]), color="orangered", linewidth=2)
plt.title("频域信号幅值谱", fontsize=16)
plt.xlabel("频率 (Hz)")
plt.ylabel("幅值")
plt.show()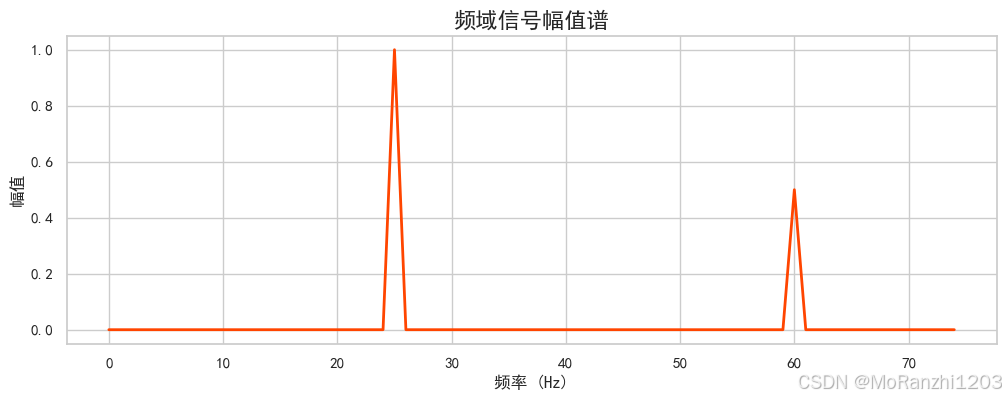

频域图直观反映了信号主要的频率成分，峰值对应于正弦波的基频与谐波位置。

---

3. 窗函数与频谱泄漏

由于实际信号往往被截断为有限长度，直接进行傅里叶变换会产生频谱泄漏现象。此时，频域中的能量会从主频扩散到邻近频率区域，使得频谱不够清晰。

设信号应用窗函数 w[n]w[n]w[n] 后为：
xw[n]=x[n]⋅w[n],w[n]={1,0≤n<N0,otherwise x_w[n] = x[n] \cdot w[n], \quad w[n] = \begin{cases} 1, & 0 \le n < N \\ 0, & \text{otherwise} \end{cases} xw[n]=x[n]⋅w[n],w[n]={1,0,0≤n<Notherwise

对应的频域卷积为：
Xw(ω)=X(ω)∗W(ω) X_w(\omega) = X(\omega) * W(\omega) Xw(ω)=X(ω)∗W(ω)

为了减少泄漏，我们可使用平滑窗函数，如 Blackman 窗。下例展示了其效果：

from scipy.signal.windows import blackman
from scipy.fft import fft

N = len(x)
w = blackman(N)
Xw = fft(x*w)
mask = freqs >= 0

plt.figure(figsize=(12,4))
sns.lineplot(x=freqs[mask], y=2.0/N*np.abs(X[mask]), label='无窗FFT', color="dodgerblue", linewidth=2)
sns.lineplot(x=freqs[mask], y=2.0/N*np.abs(Xw[mask]), label='Blackman窗FFT', color="orangered", linewidth=2)
plt.title("窗函数对频谱泄漏的影响", fontsize=16)
plt.xlabel("频率 (Hz)")
plt.ylabel("幅值")
plt.legend()
plt.show()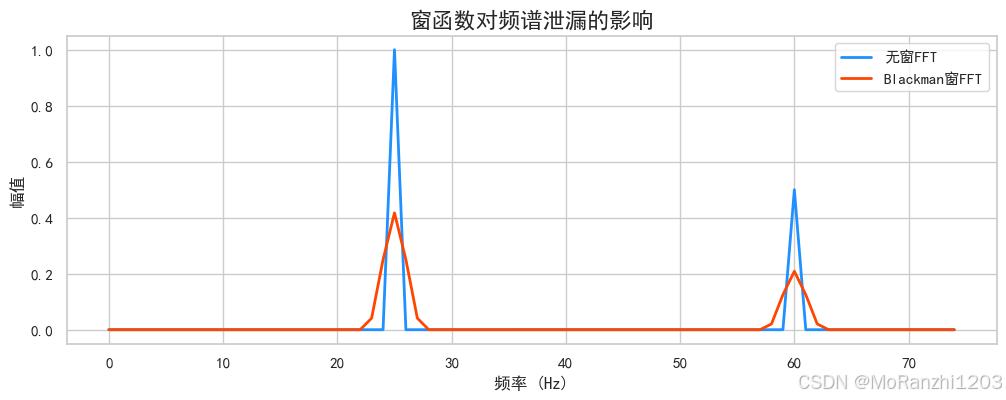

---

4. 实值序列优化：rfft 与 irfft

对于实值信号，其负频率部分是正频率的复共轭，因此在计算时仅需保留一半频率区间即可，从而减少一半运算量。

其数学形式为：
Xr[k]=∑n=0N−1x[n]e−i2πkn/N,k=0,...,N/2 X_r[k] = \sum_{n=0}^{N-1} x[n] e^{-i 2\pi k n / N}, \quad k=0,\dots,N/2 Xr[k]=n=0∑N−1x[n]e−i2πkn/N,k=0,...,N/2

以下示例展示了使用 rfft 与 irfft 的信号变换与恢复过程：

from scipy.fft import rfft, irfft

Xr = rfft(x)
x_rec = irfft(Xr, n=len(x))

plt.figure(figsize=(12,4))
sns.lineplot(x=t, y=x, color="dodgerblue", linewidth=3, alpha=0.8, label="原信号")
sns.lineplot(x=t, y=x_rec, color="orangered", linestyle="--", linewidth=1.2, label="rFFT恢复信号")
plt.title("实值序列 rFFT 与逆变换", fontsize=16)
plt.xlabel("时间 (s)")
plt.ylabel("幅值")
plt.legend(loc="upper right")
plt.show()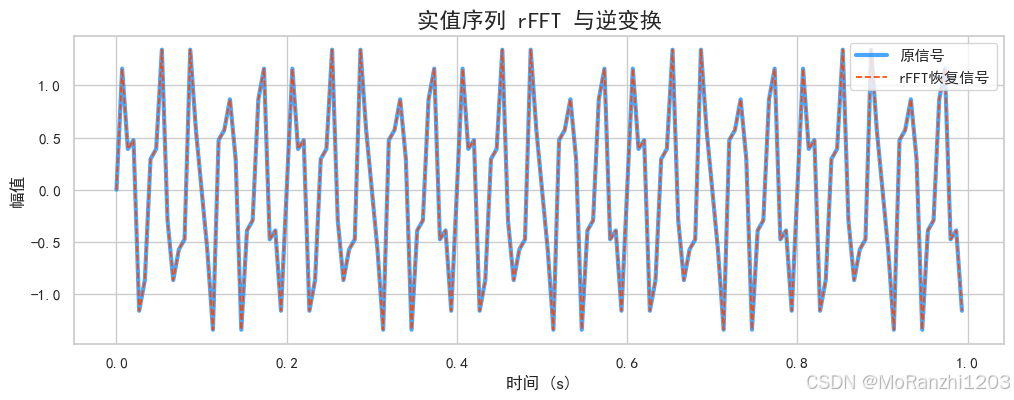

从结果可见，rFFT 的逆变换几乎完美重建原始信号，这种优化在处理大量实值数据（如声音或传感器信号）时尤为高效。

---

5. 二维傅里叶变换（2-D DFT）与图像处理

在图像处理中，二维傅里叶变换（2D-FFT）常用于边缘检测、滤波和特征提取。其数学定义如下：
X[k,l]=∑m=0M−1∑n=0N−1x[m,n]e−i2π(km/M+ln/N) X[k,l] = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} x[m,n] e^{-i 2 \pi (k m / M + l n / N)} X[k,l]=m=0∑M−1n=0∑N−1x[m,n]e−i2π(km/M+ln/N)

逆变换为：

x[m,n]=1MN∑k=0M−1∑l=0N−1X[k,l]ei2π(km/M+ln/N) x[m,n] = \frac{1}{MN} \sum_{k=0}^{M-1} \sum_{l=0}^{N-1} X[k,l] e^{i 2 \pi (k m / M + l n / N)} x[m,n]=MN1k=0∑M−1l=0∑N−1X[k,l]ei2π(km/M+ln/N)

下面的 Python 示例展示了二维信号（图像）的频谱分析与可视化：

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft2, ifft2, fftshift

# 参数设置
M, N = 64, 64
x_vals = np.linspace(0, 1, M)
y_vals = np.linspace(0, 1, N)
X, Y = np.meshgrid(x_vals, y_vals)

# 构造二维信号（图像）
img = np.sin(45 * 2 * np.pi * X) + np.sin(20 * 2 * np.pi * Y)

# 傅里叶变换
F = fft2(img)
F_shifted = fftshift(F)  # 频谱居中

# 幅度谱 & 相位谱
magnitude_spectrum = np.log1p(np.abs(F_shifted))
phase_spectrum = np.angle(F_shifted)

# 可视化：原始图像 + 幅度谱 + 相位谱
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

axes[0].imshow(img, cmap="gray")
axes[0].set_title("原始图像")
axes[0].axis("off")

im1 = axes[1].imshow(magnitude_spectrum, cmap="viridis")
axes[1].set_title("幅度谱 (对数尺度)")
axes[1].axis("off")
fig.colorbar(im1, ax=axes[1], fraction=0.046, pad=0.04)

im2 = axes[2].imshow(phase_spectrum, cmap="twilight")
axes[2].set_title("相位谱")
axes[2].axis("off")
fig.colorbar(im2, ax=axes[2], fraction=0.046, pad=0.04)

plt.show()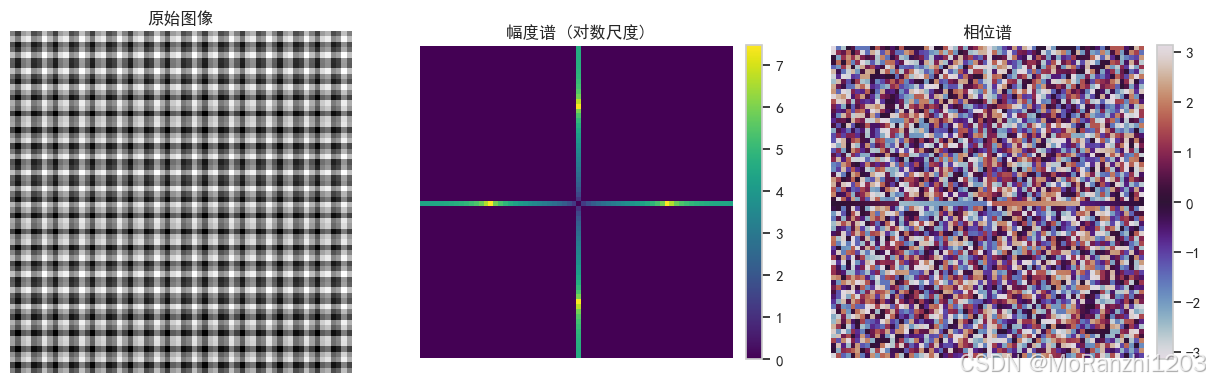

通过观察幅度谱可以识别出主要频率方向，而相位谱则记录了结构与位置等信息。这种方法在图像增强与特征分析中十分常用。

左图：原始二维信号（灰度表示），可见水平和垂直的正弦纹理。

中图：幅度谱对数显示，峰值代表图像中主要频率方向。

右图：相位谱，记录了图像结构和位置信息，决定图像形状。

# 频谱切片 (取中心横向 & 纵向)
center_x = M // 2
center_y = N // 2

horizontal_slice = magnitude_spectrum[center_y, :]
vertical_slice = magnitude_spectrum[:, center_x]

fig, axes = plt.subplots(1, 2, figsize=(12, 4))

axes[0].plot(horizontal_slice, color="steelblue")
axes[0].set_title("频谱横向切片 (中间行)")
axes[0].set_xlabel("频率索引")
axes[0].set_ylabel("幅度 (log)")

axes[1].plot(vertical_slice, color="darkorange")
axes[1].set_title("频谱纵向切片 (中间列)")
axes[1].set_xlabel("频率索引")
axes[1].set_ylabel("幅度 (log)")

plt.tight_layout()
plt.show()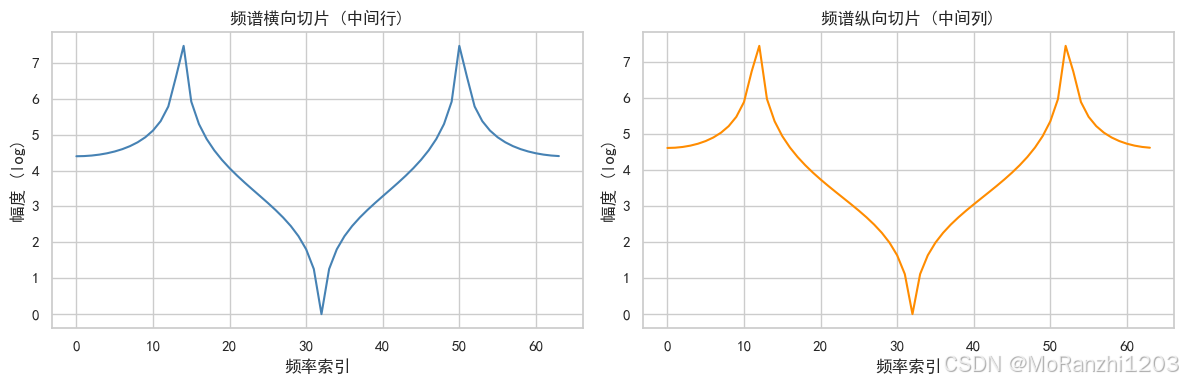

• 横向切片展示图像在水平方向的频率分布，高峰表示主要的水平频率成分。
• 纵向切片展示垂直方向的频率分布，高峰对应主要垂直纹理。

通过逆二维傅里叶变换，可以从频域信息重建原图：

# 逆变换恢复图像
img_rec = np.real(ifft2(F))

plt.figure(figsize=(6, 6))
plt.imshow(img_rec, cmap="gray")
plt.title("逆变换恢复图像")
plt.axis("off")
plt.show()

重建图像几乎与原始图像一致，说明 FFT 与 IFFT 可以完整地保存图像信息。

幅度谱决定图像能量分布，而相位谱决定图像结构和位置。

---

6. 离散余弦变换（DCT）及信号压缩

在信号处理与数据压缩中，离散余弦变换（Discrete Cosine Transform, DCT）是一种极为重要的能量压缩变换。与离散傅里叶变换（DFT）不同，DCT 仅使用实数余弦基函数，因此在保持主要信号能量的同时，能有效降低计算复杂度。

DCT 的数学定义为：

X[k]=∑n=0N−1x[n]cos⁡[πN(n+0.5)k],k=0,1,...,N−1 X[k] = \sum_{n=0}^{N-1} x[n] \cos\Big[\frac{\pi}{N} (n + 0.5) k \Big], \quad k=0,1,\dots,N-1 X[k]=n=0∑N−1x[n]cos[Nπ(n+0.5)k],k=0,1,...,N−1

逆变换（IDCT）为：
x[n]=12X[0]+∑k=1N−1X[k]cos⁡[πNk(n+0.5)] x[n] = \frac{1}{2} X[0] + \sum_{k=1}^{N-1} X[k] \cos\Big[\frac{\pi}{N} k (n + 0.5)\Big] x[n]=21X[0]+k=1∑N−1X[k]cos[Nπk(n+0.5)]

这种变换具有良好的能量集中特性，大多数自然信号的主要能量会集中在前几个系数上，因此可以截断高频分量以实现压缩。

from scipy.fft import dct, idct

X_dct = dct(x, type=2, norm='ortho')
X_compressed = X_dct.copy()
X_compressed[int(0.5*len(X_dct)):] = 0  # 压缩：保留前50%

x_rec = idct(X_compressed, type=2, norm='ortho')

plt.figure(figsize=(12,4))
sns.lineplot(x=t, y=x, color="dodgerblue", linewidth=2, label="原信号")
sns.lineplot(x=t, y=x_rec, color="orangered", linestyle="--", linewidth=2, label="DCT压缩恢复信号")
plt.title("DCT压缩效果", fontsize=16)
plt.xlabel("时间 (s)")
plt.ylabel("幅值")
plt.legend(loc="upper right")
plt.show()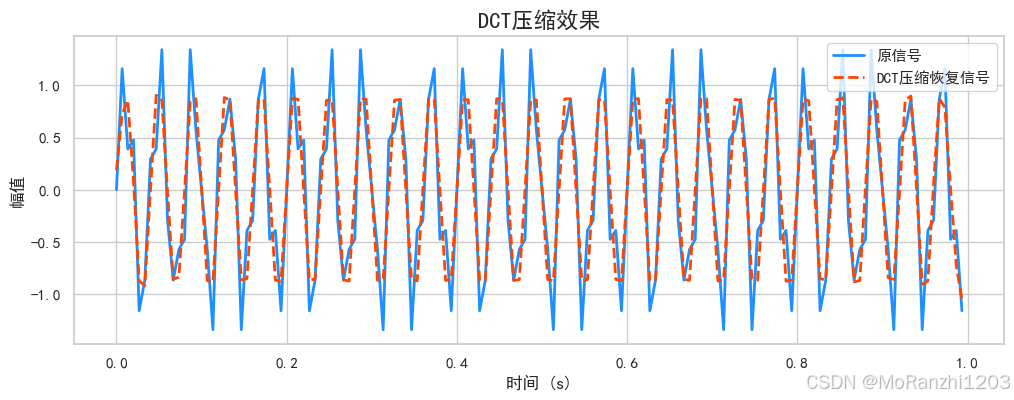

上图展示了信号在经过 DCT 压缩后再通过 IDCT 逆变换恢复的结果。可以观察到，尽管高频分量被舍弃，信号的主要形状与幅值仍得以保留。

为了更直观地观察能量的集中分布，我们绘制 DCT 系数的能量谱。大部分能量集中在低频部分，这正是 DCT 在压缩应用中的关键优势。

plt.figure(figsize=(12,4))
sns.lineplot(x=np.arange(len(X_dct)), y=np.abs(X_dct), color="purple", linewidth=2)
plt.title("DCT 系数能量分布", fontsize=16)
plt.xlabel("系数索引", fontsize=12)
plt.ylabel("幅值", fontsize=12)
plt.show()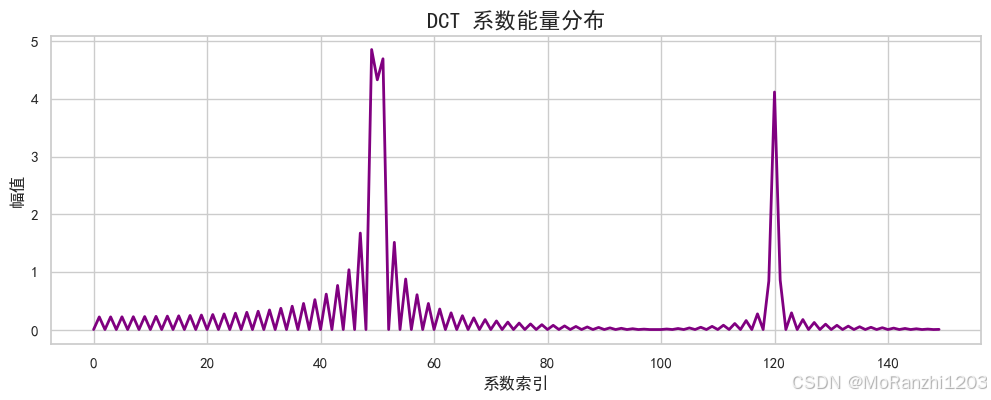

---

7. 总结

傅里叶变换及其扩展方法（FFT、rFFT、2D-FFT、DCT）是信号分析与处理的核心工具。

通过掌握其数学原理和 SciPy 实现，你可以在一维信号、实值序列以及二维图像中高效完成频域分析、频谱优化、信号重建与压缩处理。窗函数可抑制频谱泄漏，rFFT 提升实值信号计算效率，二维傅里叶变换揭示图像的幅度与相位特征，而 DCT 则实现高效能量压缩。

综合运用这些方法，既能深入理解信号本质，也能为科学计算和工程实践提供高效可靠的工具。