最短路径问题总结

文章目录

简介
复杂问题
解释
- 框架主要结构
- 研究方向与应用
案例
- [多目标（期望、方差、CVaR） + 随机边权 + 有向图 + 全源（对所有节点对）](#多目标（期望、方差、CVaR） + 随机边权 + 有向图 + 全源（对所有节点对）)
- 一、案例说明（问题设置）
- [二、Python 实现](#二、Python 实现)
- 三、示例结果（部分摘录）
- 四、代码要点与如何扩展到更复杂/现实场景
- 五、下一步
另一个案例

简介

按路径数量与需求分类

单源最短路径问题（Single-Source Shortest Path, SSSP）

➤ 从一个起点到图中所有其他节点的最短路径。
- 常用算法：Dijkstra算法、Bellman-Ford算法。
单目标最短路径问题（Single-Destination Shortest Path）

➤ 所有节点到同一个终点的最短路径（可以通过反向边转化为单源问题）。
单对最短路径问题（Single-Pair Shortest Path, SPSP）

➤ 只求两个特定节点之间的最短路径。
全源最短路径问题（All-Pairs Shortest Path, APSP）

➤ 求图中任意两个节点之间的最短路径。
- 常用算法：Floyd--Warshall算法、Johnson算法。

按图的性质分类

有向图最短路径问题
无向图最短路径问题
带权图最短路径问题（权值可正可负）
非负权图最短路径问题（如Dijkstra适用）
负权图最短路径问题（需Bellman-Ford或Floyd算法）

按约束或扩展形式分类

K最短路径问题（K-Shortest Paths Problem）
➤ 求前K条最短的路径。
受约束最短路径问题（Constrained Shortest Path Problem, CSPP）
➤ 在最短路径的同时满足某些约束（如时间、容量、风险等）。
多目标最短路径问题（Multi-objective Shortest Path Problem）
➤ 同时优化多个目标（如时间和费用）。
随机最短路径问题（Stochastic Shortest Path Problem）
➤ 边的长度具有不确定性或概率分布。
动态最短路径问题（Dynamic Shortest Path Problem）
➤ 网络结构或权值随时间变化。
增量最短路径问题（Incremental Shortest Path）
➤ 网络变化较小，更新最短路径而非重新计算。
多源多目标最短路径问题（Multi-Source Multi-Destination）
➤ 多个起点与终点组合求最优连接。

如果按常见分类来算，最短路径问题主要包括：

分类角度	常见类型	数量
按路径数量	单源、单目标、单对、全源	4类
按约束扩展	K最短、受约束、多目标、随机、动态、增量、多源多目标等	6～8类以上
按图结构	有向、无向、带权、非负权、负权	4～5类

复杂问题

✅ 全源最短路径问题（All-Pairs Shortest Path, APSP）
✅ 有向图最短路径问题
✅ 多目标最短路径问题（Multi-objective Shortest Path Problem, MOSP）
✅ 随机或不确定性边权（Stochastic Shortest Path Problem, SSPP）

这些如果同时结合 ，确实会形成一种高度复杂的复合型最短路径问题 ，而且在理论研究与应用中是存在的。

复合型问题的定义

这个综合问题可以被描述为：

多目标随机全源最短路径问题（Multi-objective Stochastic All-Pairs Shortest Path Problem on Directed Graphs, MOS-APSP）

问题特征

图类型： 有向图 G = ( V , E ) G = (V, E) G=(V,E)
边权： 每条边 e ∈ E e \in E e∈E 的长度是一个随机变量 w e w_e we，具有概率分布（如正态、指数或经验分布）
目标函数： 不止一个目标，比如：
- 最小化期望路径长度 E [ L ( P ) ] \mathbb{E}[L(P)] E[L(P)]
- 最小化路径方差 V a r ( L ( P ) ) Var(L(P)) Var(L(P))
- 最小化风险度量（如CVaR、VaR）
- 甚至同时考虑费用、时间、能耗等
全源目标： 求出所有节点对 ( i , j ) (i, j) (i,j) 之间的帕累托最优路径集（Pareto-optimal set）

数学形式（概念层面）

设路径 P i j P_{ij} Pij 是从节点 i i i 到节点 j j j 的可行路径集合，

则每条路径的随机代价为：

C ( P i j ) = ∑ e ∈ P i j w e C(P_{ij}) = \sum_{e \in P_{ij}} w_e C(Pij)=e∈Pij∑we

优化目标为：

min ⁡ P i j f ( P i j ) = ( E [ C ( P i j ) ] , V a r [ C ( P i j ) ] , Cost ( P i j ) , ... ) \min_{P_{ij}} \, \mathbf{f}(P_{ij}) = ( \mathbb{E}[C(P_{ij})], \, Var[C(P_{ij})], \, \text{Cost}(P_{ij}), \ldots ) Pijminf(Pij)=(E[C(Pij)],Var[C(Pij)],Cost(Pij),...)

并寻找所有节点对的非支配解集（Pareto front）。

难度与复杂性

这种组合问题的复杂度极高：

特性	复杂性来源
全源	要求 ( O(	V	^2) ) 个节点对
多目标	需要生成帕累托前沿（通常是指数复杂度）
随机性	边权期望与分布计算，可能需采样或仿真
有向性	无法简化为对称结构，加剧计算难度

因此该问题属于 NP-hard ，在大多数情况下无法精确求解 ，只能使用启发式或近似算法。

常见研究方法

学术界确实有研究这类问题，但通常用不同名称或分步处理：

方法类别	代表算法/思路	说明
多目标进化算法	NSGA-II, MOEA/D	处理帕累托前沿近似
随机优化	Monte Carlo sampling, CVaR优化	处理不确定边权
近似动态规划	Stochastic Dynamic Programming	处理期望和风险
分层求解	先单源→再全源	降低计算复杂度
混合模型	模糊-随机最短路径 (Fuzzy-Stochastic Shortest Path)	同时考虑模糊与随机性

学术存在性

这类问题虽然很复杂，但确实存在研究方向。例如：

"Multi-objective stochastic shortest path problems"
（European Journal of Operational Research, 2018）
"A stochastic multi-objective shortest path model for uncertain networks"
（Transportation Research Part B, 2020）
"Multi-objective all-pairs shortest path problem with uncertain edge weights"
（Applied Soft Computing, 2023）

这些文献都在研究你描述的问题组合的部分或整体形式。

全源 + 有向 + 多目标 + 随机"的最短路径问题确实存在，

一般称为 多目标随机全源最短路径问题（MOS-APSP） ，

是一种极其复杂、NP难的高级运筹学问题，目前多用启发式或近似算法求解。

解释

框架主要结构

1️⃣ 输入层（Input）

有向图 G = ( V , E ) G = (V, E) G=(V,E)
边权：随机变量 w e ∼ P e ( x ) w_e \sim P_e(x) we∼Pe(x)
多个优化目标函数（期望、方差、风险、成本）
可能的约束条件（容量、时间、资源等）

2️⃣ 模型层（Model）

随机建模模块（处理不确定性）
多目标优化模块（构建多目标函数 f ( P ) \mathbf{f}(P) f(P)）
帕累托支配关系定义

3️⃣ 算法层（Algorithm）

随机采样 / Monte Carlo 模块
多目标进化算法（如 NSGA-II、MOEA/D）
随机动态规划或启发式搜索
收敛准则与复杂度控制

4️⃣ 输出层（Output）

帕累托最优路径集（Pareto-optimal paths）
全源最短路径矩阵（Expected shortest paths）
风险-收益前沿图（Risk--Performance Frontier）

研究方向与应用

研究方向	内容说明	应用场景
算法设计	结合进化算法与随机仿真，求解大规模MOS-APSP	智能交通、物流网络
风险建模	使用CVaR、VaR、熵等度量路径风险	供应链与金融网络
分布式求解	并行或GPU加速算法	大规模通信网络
数据驱动优化	基于历史数据估计边权分布	智慧城市与运输预测

案例

多目标（期望、方差、CVaR） + 随机边权 + 有向图 + 全源（对所有节点对）

一、案例说明（问题设置）

图：有向图 G = ( V , E ) G=(V,E) G=(V,E)，节点 V = { A , B , C , D , E } V=\{A,B,C,D,E\} V={A,B,C,D,E}。
每条有向边 e = ( u , v ) e=(u,v) e=(u,v) 有随机权重，假设服从正态分布 N ( μ e , σ e ) N(\mu_e,\sigma_e) N(μe,σe)，并在采样后把负值截为 0（代表时间/长度不可为负）。
优化目标（多目标示例）：
1. 期望路径长度 E [ L ( P ) ] \mathbb{E}[L(P)] E[L(P)]（最小化）
2. 路径长度方差 V a r ( L ( P ) ) \mathrm{Var}(L(P)) Var(L(P))（最小化）
3. 另外计算 CVaR_{0.95} 作为风险度量（方便分析）
求解方式（示例实现）：
- 枚举每个节点对的所有简单路径（受 hops 上限限制，示例中用 max hops = 6）
- 对每条路径进行 Monte Carlo 采样（示例中 2000 次），估计 mean、variance、CVaR(0.95)
- 对每个节点对构建帕累托前沿（在 mean 与 variance 两目标下做非支配筛选）

注意：此方法适合小图做教学或验证；实际大规模网络通常用 K-shortest 路径、启发式或进化算法（如 NSGA-II）与并行化采样来近似帕累托前沿。

二、Python 实现

我在交互环境中运行的代码完成了上面步骤（蒙特卡洛样本数 2000）。关键点如下：

自定义有向图和每条边的 (mean, std)：
- 例如 ("A","B"):(5.0, 1.0) 表示边 A→B 的权重 ~ N(5,1)
枚举简单路径（DFS，跳数上限避免组合爆炸）
对每条路径采样，计算 mean、variance、CVaR(0.95)
为每个 (src,dst) 计算 Pareto front（在 mean 和 variance 两目标下）

我把所有评估路径表 和每个节点对的 Pareto 前沿摘要输出（环境会把表格展示给你）。并且在控制台中打印了每个对的 Pareto 前沿示例（你可以看到路径字符串、平均值、方差、CVaR）。

三、示例结果（部分摘录）

下面是示例运行时打印的若干 Pareto 前沿（每行：src dst path hops mean variance cvar_0.95）：

A -> B:
- A->B, mean ≈ 4.99, var ≈ 0.916, CVaR_0.95 ≈ 6.95
A -> C:
- A->C, mean ≈ 1.98, var ≈ 0.238, CVaR_0.95 ≈ 2.99
A -> D:
- A->C->D, mean ≈ 4.52, var ≈ 0.946, CVaR_0.95 ≈ 6.50
A -> E:
- A->C->D->E, mean ≈ 5.51, var ≈ 0.964, CVaR_0.95 ≈ 7.50
B -> E:
- B->D->E and B->C->D->E 都可能出现在 Pareto 集（示例中两条路径的 mean/var 都很接近）
D -> E:
- D->E, mean ≈ 0.998, var ≈ 0.041, CVaR_0.95 ≈ 1.42

（上面为示例数值，因 Monte Carlo 有随机性，重新运行会有微小差别）

四、代码要点与如何扩展到更复杂/现实场景

路径枚举 vs K-shortest
- 枚举所有简单路径适用于节点数小的图。现实大型网络常用 K-shortest（Yen 算法）、或启发式生成候选路径来限制搜索空间。
采样（Monte Carlo）
- 用于估计随机路径代价分布。可以使用重要抽样、分布拟合或参数化近似来降低样本需求。
多目标求解
- 本例用显式非支配判断得到 Pareto 集。如果目标或路径过多，常用多目标进化算法（NSGA-II、MOEA/D）直接在路径或路径编码上进化。
风险度量
- CVaR 是常用度量，也可用 VaR、概率约束（P(L>t)<ε）、或用户定义的效用函数。
并行化/分布式
- Monte Carlo 及多对并行评估天然适合并行化（多核/GPU/集群）。
数据驱动
- 边权分布可由历史数据拟合（正态、伽马、经验分布等），也可使用时间序列模型（若边权随时间相关）。

五、下一步

把示例扩展为**使用 K-shortest 路径（Yen）**而不是简单枚举（如果你想要我可以实现）
改成单目标 + CVaR 约束 或多目标进化（NSGA-II）示例，并运行演示（会展示近似帕累托前沿）
更换边权分布（比如泊松、对数正态或经验分布），或导入自己的网络/边权数据进行实测

bash 复制代码

import random
import math
import itertools
import pandas as pd
import numpy as np

# Utility to show DataFrame in UI (provided by environment)
try:
    from caas_jupyter_tools import display_dataframe_to_user
    has_display = True
except Exception:
    has_display = False

# --------------- Define a small directed graph ----------------
# Nodes: A,B,C,D,E
# Edges: (u,v): (mean, std)
nodes = ["A","B","C","D","E"]
edges = {
    ("A","B"):(5.0, 1.0),
    ("A","C"):(2.0, 0.5),
    ("B","C"):(1.5, 0.3),
    ("B","D"):(4.0, 1.2),
    ("C","D"):(2.5, 0.8),
    ("C","E"):(7.0, 2.0),
    ("D","E"):(1.0, 0.2),
    ("B","E"):(12.0, 3.0),
    ("A","D"):(9.0, 2.5)
}

# Build adjacency list
adj = {n:[] for n in nodes}
for (u,v) in edges:
    adj[u].append(v)
    
# --------------- Path enumeration (simple paths) ----------------
def enumerate_simple_paths(src, dst, max_hops=5):
    """Enumerate simple paths from src to dst using DFS up to max_hops nodes (inclusive)."""
    results = []
    stack = [(src, [src])]
    while stack:
        node, path = stack.pop()
        if len(path) > max_hops: 
            continue
        for nei in adj.get(node, []):
            if nei in path:
                continue
            newp = path + [nei]
            if nei == dst:
                results.append(newp)
            else:
                stack.append((nei, newp))
    return results

# --------------- Path cost sampling ----------------
def sample_path_cost(path, n_samples=2000, seed=None):
    """Monte Carlo sample total cost along path. Each edge cost ~ Normal(mean, std), truncated to >=0."""
    if seed is not None:
        np.random.seed(seed)
    samples = np.zeros(n_samples)
    for i in range(len(path)-1):
        u,v = path[i], path[i+1]
        mu, sigma = edges[(u,v)]
        # sample normal and truncate at 0 (no negative travel time)
        s = np.random.normal(loc=mu, scale=sigma, size=n_samples)
        s = np.maximum(s, 0.0)
        samples += s
    return samples

def path_statistics(samples, alpha=0.95):
    mean = samples.mean()
    var = samples.var(ddof=1)
    # CVaR at level alpha: average of worst (1-alpha) tail
    cutoff = np.quantile(samples, alpha)
    tail = samples[samples >= cutoff]
    cvar = tail.mean() if len(tail)>0 else cutoff
    return {"mean": mean, "variance": var, "cvar_{}".format(alpha): cvar}

# --------------- Pareto (non-dominated) selection ----------------
def pareto_front(df, objectives):
    """Return boolean mask of non-dominated rows in df for given objectives (all minimized)."""
    data = df[objectives].values
    n = data.shape[0]
    is_pareto = np.ones(n, dtype=bool)
    for i in range(n):
        if not is_pareto[i]:
            continue
        # any other point that strictly dominates i?
        for j in range(n):
            if i==j: continue
            # j dominates i if j<=i in all objectives and < in at least one
            if np.all(data[j] <= data[i]) and np.any(data[j] < data[i]):
                is_pareto[i] = False
                break
    return is_pareto

# --------------- Run for all pairs ----------------
results_all = []

# restrict to reasonable path length for demo
MAX_HOPS = 6
SAMPLES = 2000

for src in nodes:
    for dst in nodes:
        if src==dst: 
            continue
        paths = enumerate_simple_paths(src, dst, max_hops=MAX_HOPS)
        if not paths:
            continue
        for p in paths:
            samples = sample_path_cost(p, n_samples=SAMPLES)
            stats = path_statistics(samples, alpha=0.95)
            results_all.append({
                "src": src,
                "dst": dst,
                "path": "->".join(p),
                "hops": len(p)-1,
                "mean": stats["mean"],
                "variance": stats["variance"],
                "cvar_0.95": stats["cvar_0.95"]
            })

df = pd.DataFrame(results_all)
df_sorted = df.sort_values(["src","dst","mean"]).reset_index(drop=True)

# find pareto front per (src,dst) w.r.t. (mean, variance)
pareto_summary = []
pareto_details = {}
for (src,dst), group in df_sorted.groupby(["src","dst"]):
    mask = pareto_front(group, objectives=["mean","variance"])
    pareto = group[mask].copy().reset_index(drop=True)
    pareto_details[(src,dst)] = pareto
    pareto_summary.append({
        "src": src, "dst": dst, "n_paths": len(group), "n_pareto": len(pareto),
        "best_mean": group['mean'].min(), "best_variance": group['variance'].min()
    })

df_summary = pd.DataFrame(pareto_summary).sort_values(["src","dst"]).reset_index(drop=True)

# Display results
if has_display:
    display_dataframe_to_user("All evaluated paths (sample estimates)", df_sorted)
    display_dataframe_to_user("Pareto front summary per node pair", df_summary)
else:
    print("All evaluated paths (first 20 rows):")
    print(df_sorted.head(20).to_string(index=False))
    print("\nPareto front summary per node pair:")
    print(df_summary.to_string(index=False))

# Also print detailed pareto fronts for each pair in console output (helps user read results)
for key, pareto_df in pareto_details.items():
    print(f"\nPareto front for {key[0]} -> {key[1]} (n={len(pareto_df)})")
    print(pareto_df.sort_values(["mean","variance"]).to_string(index=False))

另一个案例

运筹学复合问题 ，结合了路径规划 、任务分配 和物流调度思想。

一个标准的、可建模的科学问题（运筹学/优化模型）。

一、情境重述

"一个快递员要从一个城市送货到另一个城市，取一次货就送一个点，然后到另一个取货点，再送到另一个不同点。"

可以理解为：

快递员从一个起点（配送中心）出发；
必须完成一系列"取货--送货"任务；
每个任务是一个 取货点 → 送货点；
每完成一次送货后，再前往下一个取货点；
目标：最短距离、最小成本、或最少时间；
可能还存在时间窗、容量、优先级等约束。

二、科学建模方向（核心思想）

问题归类

这个问题属于：

带取送货的旅行商问题（Pickup and Delivery Traveling Salesman Problem, PD-TSP）

或者更一般地：

单车单人带取送货的车辆路径问题（Single-Vehicle Pickup and Delivery Problem, 1-PDP）

如果有多辆车，则称为：

车辆路径问题带取送货（VRPPD: Vehicle Routing Problem with Pickup and Delivery）

三、数学建模（简化版）

设：

有一组任务 T = { 1 , 2 , . . . , n } T = \{1,2,...,n\} T={1,2,...,n}
每个任务 i i i 有两个位置：取货点 p i p_i pi，送货点 d i d_i di
节点集合 N = { 0 , p 1 , d 1 , . . . , p n , d n , 2 n + 1 } N = \{0, p_1, d_1, ..., p_n, d_n, 2n+1\} N={0,p1,d1,...,pn,dn,2n+1}
- 0 0 0：出发城市（仓库）
- 2 n + 1 2n+1 2n+1：返回终点（可为同一城市）

定义：

c i j c_{ij} cij：从节点 i i i 到节点 j j j 的行驶成本（或距离/时间）
决策变量：

x i j = { 1 , 若快递员从点 i 到 j 0 , 否则 x_{ij} = \begin{cases} 1, & \text{若快递员从点 } i \text{ 到 } j\\ 0, & \text{否则} \end{cases} xij={1,0,若快递员从点 i 到 j否则

目标函数：

最小化总成本：

min ⁡ ∑ i ∑ j c i j x i j \min \sum_{i}\sum_{j} c_{ij}x_{ij} mini∑j∑cijxij

约束条件：

每个节点访问一次

∑ i x i j = 1 , ∑ j x i j = 1 \sum_{i} x_{ij} = 1, \quad \sum_{j} x_{ij} = 1 i∑xij=1,j∑xij=1
取货必须在送货之前

t p i < t d i ∀ i t_{p_i} < t_{d_i} \quad \forall i tpi<tdi∀i

（可以用顺序或前后约束线性化）
载重约束（如果有）

q k + q i ≤ Q ( 快递员车辆容量 ) q_k + q_i \le Q \quad (\text{快递员车辆容量}) qk+qi≤Q(快递员车辆容量)
时间窗约束（如果有限时要求）

e i ≤ t i ≤ l i e_i \le t_i \le l_i ei≤ti≤li

四、模型解释

模型部分	实际意义
目标函数	总路程最短或总时间最短
访问约束	每个取送货点都必须访问一次
顺序约束	保证"先取货再送货"
载重约束	模拟快递车容量
时间窗约束	模拟取送件时间要求

五、扩展版本

这个问题可以进一步演化为许多重要的研究方向：

扩展类型	描述
多车辆	多个快递员或配送车，变成 VRPPD
动态取送货	新任务实时到达（Dynamic PD Problem）
随机旅行时间/需求	加入不确定性（Stochastic PDP）
多目标优化	同时优化时间、成本、客户满意度等
时间窗约束	客户有预约时间（PDPTW）
带装载顺序	物品装载有顺序要求（例如后取的要先放）

六、科学定义

单车辆带取送货的路径优化问题（Single-Vehicle Pickup and Delivery Problem, 1-PDP）

目标是在满足"取货先于送货"约束的前提下，使快递员完成所有任务的总成本最小。

python

bash 复制代码

# ================================================================
# 单车辆带取送货的路径优化问题（Pickup & Delivery Problem）
# 含方向箭头 + 左右分布布局（取货左、送货右）
# ================================================================
from ortools.constraint_solver import pywrapcp, routing_enums_pb2
import numpy as np
import matplotlib.pyplot as plt
import random

# ---------------------------
# 1. 数据定义
# ---------------------------
# 仓库：在中间稍偏左
coords = {
    0: (1, 3),   # 仓库起点
    1: (random.uniform(0, 3), random.uniform(1, 5)),  # 取货A
    2: (random.uniform(6, 9), random.uniform(1, 5)),  # 送货A
    3: (random.uniform(0, 3), random.uniform(1, 5)),  # 取货B
    4: (random.uniform(6, 9), random.uniform(1, 5)),  # 送货B
    5: (1, 3)    # 仓库终点
}

# ---------------------------
# 2. 距离矩阵
# ---------------------------
def euclidean_distance_matrix(coords):
    n = len(coords)
    matrix = np.zeros((n, n))
    for i in range(n):
        for j in range(n):
            if i != j:
                xi, yi = coords[i]
                xj, yj = coords[j]
                matrix[i, j] = round(((xi - xj)**2 + (yi - yj)**2)**0.5, 2)
    return matrix

dist_matrix = euclidean_distance_matrix(coords)

# ---------------------------
# 3. 构建模型
# ---------------------------
manager = pywrapcp.RoutingIndexManager(len(dist_matrix), 1, [0], [5])
routing = pywrapcp.RoutingModel(manager)

def distance_callback(from_index, to_index):
    from_node = manager.IndexToNode(from_index)
    to_node = manager.IndexToNode(to_index)
    return int(dist_matrix[from_node][to_node] * 100)

transit_callback_index = routing.RegisterTransitCallback(distance_callback)
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)

# 添加距离维度（Distance Dimension）
routing.AddDimension(
    transit_callback_index,
    0,
    100000,
    True,
    "Distance"
)
distance_dimension = routing.GetDimensionOrDie("Distance")

# ---------------------------
# 4. 取送货约束
# ---------------------------
pickups_deliveries = [(1, 2), (3, 4)]
for pickup, delivery in pickups_deliveries:
    routing.AddPickupAndDelivery(manager.NodeToIndex(pickup), manager.NodeToIndex(delivery))
    routing.solver().Add(
        routing.VehicleVar(manager.NodeToIndex(pickup)) == routing.VehicleVar(manager.NodeToIndex(delivery))
    )
    routing.solver().Add(
        distance_dimension.CumulVar(manager.NodeToIndex(pickup)) <=
        distance_dimension.CumulVar(manager.NodeToIndex(delivery))
    )

# ---------------------------
# 5. 容量约束
# ---------------------------
def demand_callback(from_index):
    node = manager.IndexToNode(from_index)
    if node in [1, 3]:  # 取货点
        return 1
    elif node in [2, 4]:  # 送货点
        return -1
    else:
        return 0

demand_callback_index = routing.RegisterUnaryTransitCallback(demand_callback)
routing.AddDimensionWithVehicleCapacity(
    demand_callback_index,
    0,
    [1],
    True,
    "Capacity"
)

# ---------------------------
# 6. 搜索参数
# ---------------------------
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
search_parameters.local_search_metaheuristic = routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH
search_parameters.time_limit.FromSeconds(3)

# ---------------------------
# 7. 求解
# ---------------------------
solution = routing.SolveWithParameters(search_parameters)

# ---------------------------
# 8. 输出结果
# ---------------------------
def print_solution(manager, routing, solution):
    index = routing.Start(0)
    plan_output = []
    route_distance = 0
    while not routing.IsEnd(index):
        node = manager.IndexToNode(index)
        plan_output.append(node)
        previous_index = index
        index = solution.Value(routing.NextVar(index))
        route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
    plan_output.append(manager.IndexToNode(index))
    route_distance /= 100.0
    return plan_output, route_distance

if solution:
    route, total_distance = print_solution(manager, routing, solution)
    print("🚚 最优路线（节点序列）:", route)
    print("📏 总行驶距离:", total_distance, "单位")
else:
    print("未找到可行解！")

# ---------------------------
# 9. 可视化（带箭头）
# ---------------------------
if solution:
    plt.figure(figsize=(8, 5))
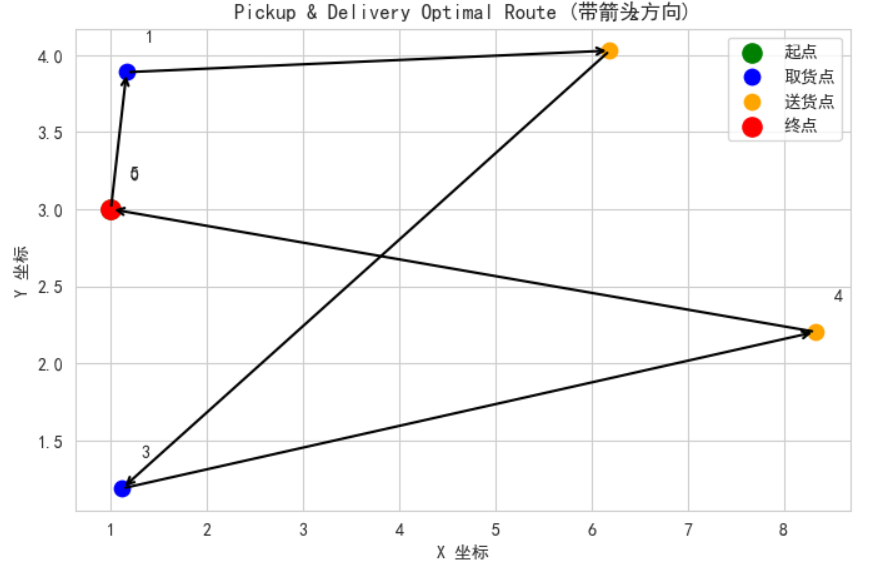
    plt.title("Pickup & Delivery Optimal Route (带箭头方向)")
    plt.xlabel("X 坐标")
    plt.ylabel("Y 坐标")

    # 绘制点
    for node, (x, y) in coords.items():
        if node == 0:
            plt.scatter(x, y, c="green", s=120, label="起点")
        elif node == 5:
            plt.scatter(x, y, c="red", s=120, label="终点")
        elif node in [1, 3]:
            plt.scatter(x, y, c="blue", s=80, label="取货点" if node == 1 else "")
        elif node in [2, 4]:
            plt.scatter(x, y, c="orange", s=80, label="送货点" if node == 2 else "")
        plt.text(x + 0.2, y + 0.2, str(node), fontsize=10)

    # 绘制带箭头的路径
    for i in range(len(route) - 1):
        x_start, y_start = coords[route[i]]
        x_end, y_end = coords[route[i + 1]]
        plt.annotate("",
                     xy=(x_end, y_end),
                     xytext=(x_start, y_start),
                     arrowprops=dict(arrowstyle="->", color="black", lw=1.5))

    plt.legend()
    plt.grid(True)
    plt.show()