BEVFUSION解读(五)
- 相机backbone特征提取
-
- 总体流程图
- [🧩 模块说明](#🧩 模块说明)
- encoder之vtransform整体流程图
-
- [🧩 模块说明](#🧩 模块说明)
- [🧩 self.encoders\["camera"\]\["vtransform"\]](#🧩 self.encoders["camera"]["vtransform"])
-
- [📘 输入与输出说明](#📘 输入与输出说明)
- [📋 示例 img\_metas 字典结构](#📋 示例 img_metas 字典结构)
- vtranform第一步将雷达的点云投影到相机平面上
-
- [1️⃣ 变量与几何意义(对应图里的 K、E)](#1️⃣ 变量与几何意义(对应图里的 K、E))
- [2️⃣ 初始化深度体素(per-batch、per-cam、per-pixel)](#2️⃣ 初始化深度体素(per-batch、per-cam、per-pixel))
- [3️⃣ 主循环:将 LiDAR 点投到各相机的像素上](#3️⃣ 主循环:将 LiDAR 点投到各相机的像素上)
-
- [(a) 先把 LiDAR 侧的增强"还原"(inverse aug)](#(a) 先把 LiDAR 侧的增强“还原”(inverse aug))
- [(b) LiDAR → Image:应用 K [ R ∣ t ] K[R|t] K[R∣t] 得到相机齐次坐标并做透视除法](#(b) LiDAR → Image:应用 K [ R ∣ t ] K[R|t] K[R∣t] 得到相机齐次坐标并做透视除法)
- [(c\) 图像增强(resize/crop/flip/rotate 等)的前向作用](#(c) 图像增强(resize/crop/flip/rotate 等)的前向作用)
- (d)可见性判断与反填充深度图(splatting)
- [4️⃣ 计算体素几何:用于 BEV 体素化/池化](#4️⃣ 计算体素几何:用于 BEV 体素化/池化)
- [5️⃣ 把代码与公式逐式对齐](#5️⃣ 把代码与公式逐式对齐)
- vtranform第二步将具有深度点云特征和图像特征进行融合
-
- [🔁 dtransform 深度分支与特征融合流程](#🔁 dtransform 深度分支与特征融合流程)
- [📦 张量形状速览](#📦 张量形状速览)
- vtranform第三步视锥转换
-
- [图像坐标系视锥点投影到 lidar 坐标系,得到视锥点云](#图像坐标系视锥点投影到 lidar 坐标系,得到视锥点云)
- BEV空间创建
- 视锥创建
- 相平面到激光雷达坐标系
-
- [1\. **后处理旋转和平移(undo post-transformation)**](#1. 后处理旋转和平移(undo post-transformation))
- [2\. **深度缩放操作**](#2. 深度缩放操作)
- [3\. **相机到激光雷达坐标系转换**](#3. 相机到激光雷达坐标系转换)
- [4\. **额外的旋转和平移变换(可选)**](#4. 额外的旋转和平移变换(可选))
- [5\. **额外的平移变换(可选)**](#5. 额外的平移变换(可选))
- 总结
相机backbone特征提取
总体流程图
🟩 input : x(1, 6, 3, 256, 704) 🟦 backbone : SwinTransformer 🟪 中间输出 : x
(6, 192, 32, 88)
(6, 384, 16, 44)
(6, 768, 8, 22) 🟦 neck : FPN 🟪 中间输出 : x
(6, 256, 32, 88)
(6, 256, 16, 44)
(不输入) x = x[0] 🟦 vtransform : DepthLSSTransform
bev_pool 🟨 output : x
(1, 80, 180, 180)
🧩 模块说明
| 模块 | 名称 | 功能说明 |
|---|---|---|
| input | 图像输入 | 输入相机的多视角图像 (batch=1, n_cam=6, channel=3, H=256, W=704) |
| backbone (SwinTransformer) | 图像主干网络 | 提取多尺度视觉特征 |
| neck (FPN) | 特征融合网络 | 将不同层级特征进行融合与通道压缩 |
| vtransform (DepthLSSTransform + bev_pool) | 特征空间变换 | 将相机视角特征映射到 BEV(鸟瞰图)空间 |
| output | 输出 BEV 特征图 | 输出空间特征 (1, 80, 180, 180) |
encoder之vtransform整体流程图
🟦 图像特征图 x 🟥 1. 融合特征、概率分布预测
(get_cam_feats) 🟦 点云 points 🟦 点云投影到图像 depth 🟨 得到 (1, 6, 118, 32, 88, 80) 的特征
包含深度概率分布与图像特征 x 🟦 self.frustum 生成规则的
(N, 6, 118, 32, 88, 3) 的 coords 🟥 2. 视锥转换 🟨 转换到 lidar 坐标系的 coords 🟥 3. BEV 池化
🧩 模块说明
| 步骤 | 模块名称 | 输入 | 输出 | 功能说明 |
|---|---|---|---|---|
| 1️⃣ | 融合特征与概率分布预测 (get_cam_feats) | 图像特征 x(1,6,256,32,88),点云 points |
(1, 6, 118, 32, 88, 80) |
将相机图像特征与空间点信息融合,预测每个像素的深度概率分布。 |
| 2️⃣ | 视锥转换 (Frustum Transform) | (N, 6, 118, 32, 88, 3) 的相机坐标 |
LiDAR 坐标系下的 coords |
通过矩阵变换与齐次坐标系转换,将点从相机系投射到 LiDAR 系。 |
| 3️⃣ | BEV 池化 (bev_pool) | LiDAR 坐标下的特征与深度分布 | BEV 平面特征图 | 将 3D 特征体积投影至鸟瞰平面,实现空间汇聚。 |
🧩 self.encoders["camera"]["vtransform"]
🟦 图像特征图 x
(6, 256, 32, 88) 🟥 self.encoders['camera']['vtransform'] 🟦 点云 points
(200k, 5) 🟦 多种矩阵
(点云文件的外参矩阵) 🟦 图像元数据 img_metas
(包含图像尺寸、路径、标定矩阵等) 🟨 输出特征 x
(1, 256, 180, 180)
📘 输入与输出说明
| 输入项 | 名称 | 形状 / 内容 | 说明 |
|---|---|---|---|
| 图像特征图 | x |
(6, 256, 32, 88) |
来自 Swin Transformer + FPN 的多视角图像特征 |
| 点云 | points |
(200k, 5) |
LiDAR 点云数据,包含坐标与强度 |
| 多种矩阵 | lidar2img, img2lidar, cam_intrinsics, cam_extrinsics |
各种外参/内参矩阵 | 用于相机与 LiDAR 坐标系的几何转换 |
| 图像元数据 | img_metas |
dict | 包含图像文件路径、时间戳、shape、标定矩阵、归一化参数等信息 |
📋 示例 img_metas 字典结构
python
dict_items([
('filename', ['6 张图像路径']),
('timestamp', 1533151603547590),
('ori_shape', (1600, 900)),
('img_shape', (1600, 900)),
('lidar2image', [6 个 4x4 矩阵]),
('pad_shape', (1600, 900)),
('scale_factor', 1.0),
('box_mode_3d', 'Box3DMode.LIDAR: 0'),
('box_type_3d', 'LiDARInstance3DBoxes'),
('img_norm_cfg', {'mean': [0.485, 0.456, 0.406], 'std': [0.229, 0.224, 0.225]}),
('token', '3e8750f331d7499e9b5123e9eb70f2e2'),
('lidar_path', './data/nuscenes/samples/LIDAR_TOP/...pcd.bin')
])vtranform第一步将雷达的点云投影到相机平面上

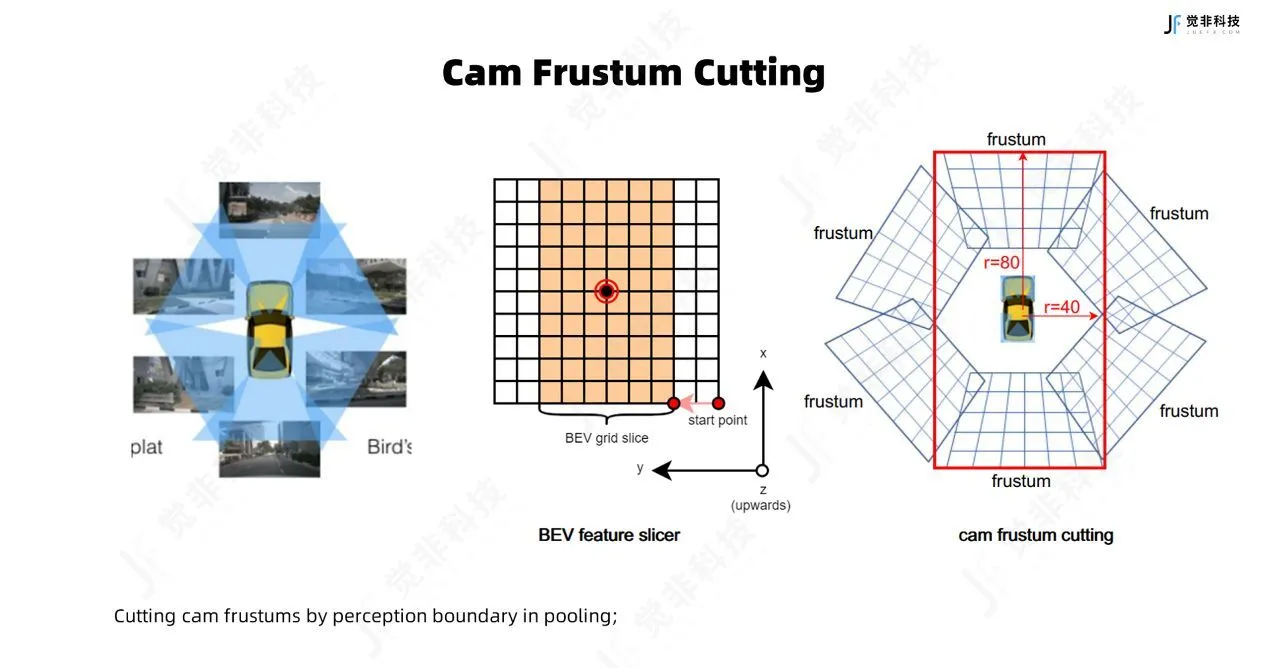
投影/变换代码按"相机内外参 → 点从 LiDAR 投到像面 → 增强矩阵 → 反填充深度图 → 为体素化取几何"的流程,结合公式图(K、E、P、P′=KEP)
1️⃣ 变量与几何意义(对应图里的 K、E)
-
intrins←cam_intrinsic[..., :3, :3]相机内参矩阵 K K K。
-
camera2lidar_rots/trans相机到 LiDAR 的外参 [ R c → l ∣ t c → l ] [R_{c\to l}\mid t_{c\to l}] [Rc→l∣tc→l]。
反之
lidar2image(下面循环里用到)等价于 K [ R l → c ∣ t l → c ] K[R_{l\to c}\mid t_{l\to c}] K[Rl→c∣tl→c]。 -
rots/trans←sensor2ego的旋转/平移传感器系(相机/雷达)到车体(ego)坐标的外参。
-
lidar2ego_rots/transLiDAR 到车体(ego)坐标的外参。
-
post_rots/post_trans←img_aug_matrix
图像增强(resize/crop/flip/rotate)的等效仿射矩阵,作用在像素坐标上。 -
extra_rots/extra_trans←lidar_aug_matrix[..., :3, :3/3]LiDAR 侧的数据增强(例如旋转/平移 jitter)。
这些矩阵与图里公式的对应关系:
-
像素齐次坐标 u ~ = [ u , v , 1 ] T \tilde{\mathbf u}=[u,v,1]^T u~=[u,v,1]T,相机坐标 x ~ c = [ x c , y c , z c , 1 ] T \tilde{\mathbf x}_c=[x_c,y_c,z_c,1]^T x~c=[xc,yc,zc,1]T,LiDAR 坐标 x ~ l = [ x l , y l , z l , 1 ] T \tilde{\mathbf x}_l=[x_l,y_l,z_l,1]^T x~l=[xl,yl,zl,1]T。
-
内参 : u ∼ K [ x c / z c , y c / z c , 1 ] T \mathbf u \sim K\,[x_c/z_c,\;y_c/z_c,\;1]^T u∼K[xc/zc,yc/zc,1]T(图中上半部分的 K K K)。
-
外参 : x c = R l → c x l + t l → c \mathbf x_c = R_{l\to c}\,\mathbf x_l + t_{l\to c} xc=Rl→cxl+tl→c(图中 E = [ R T ; 0 T 1 ] E=[R\;T;0^T\;1] E=[RT;0T1])。
-
整体投影 : u ~ ∼ K [ R l → c t l → c ] x ~ l ≜ K E ⏟ 图中 K E x ~ l \tilde{\mathbf u} \sim K\,[R_{l\to c}\;t_{l\to c}]\,\tilde{\mathbf x}l \triangleq \underbrace{K E}{\text{图中 }KE}\tilde{\mathbf x}_l u~∼K[Rl→ctl→c]x~l≜图中 KE KEx~l。
2️⃣ 初始化深度体素(per-batch、per-cam、per-pixel)
python
batch_size = len(points)
depth = torch.zeros(batch_size, img.shape[1], 1, *self.image_size)-
img.shape[1]是相机数 N_cam。 -
self.image_size = (H, W)是增强后的特征图/图像平面尺寸。 -
得到张量
depth[b, cam, 0, u, v],用来放"该相机在像素 (u,v) 上由 LiDAR 点投影得到的深度(z 或距离)"。
3️⃣ 主循环:将 LiDAR 点投到各相机的像素上
对每个 batch b:
python
cur_coords = points[b][:, :3] # LiDAR 点 (N_pts,3)
cur_img_aug_matrix = img_aug_matrix[b] # 图像增强矩阵(作用在像素)
cur_lidar_aug_matrix = lidar_aug_matrix[b] # LiDAR 增强矩阵(作用在3D)
cur_lidar2image = lidar2image[b] # 6个相机的 KE(每个相机一组)(a) 先把 LiDAR 侧的增强"还原"(inverse aug)
python
cur_coords -= cur_lidar_aug_matrix[:3, 3]
cur_coords = torch.inverse(cur_lidar_aug_matrix[:3, :3]).matmul(cur_coords.T)- 若训练/预处理对 LiDAR 做了增强(旋转/平移),这里逆变换 把点云从"增强后坐标"还原到原始 LiDAR 坐标 ,以匹配标定外参。
数学上: x l ← R aug − 1 ( x l − t aug ) \mathbf x_l \leftarrow R_{\text{aug}}^{-1}(\mathbf x_l - t_{\text{aug}}) xl←Raug−1(xl−taug)。
(b) LiDAR → Image:应用 K [ R ∣ t ] K[R|t] K[R∣t] 得到相机齐次坐标并做透视除法
python
cur_coords = cur_lidar2image[:, :3, :3].matmul(cur_coords) # R 部分
cur_coords += cur_lidar2image[:, :3, 3].reshape(-1, 3, 1) # t 部分
dist = cur_coords[:, 2, :] # z_c
cur_coords[:, 2, :] = clamp(...)
cur_coords[:, :2, :] /= cur_coords[:, 2:3, :] # 透视除法-
对每个相机 c c c: x c = R l → c x l + t l → c \mathbf x_c = R_{l\to c}\mathbf x_l + t_{l\to c} xc=Rl→cxl+tl→c。
-
透视投影: ( u ′ , v ′ ) = ( x c / z c , y c / z c ) (u',v') = (x_c/z_c,\;y_c/z_c) (u′,v′)=(xc/zc,yc/zc),并保留
dist=z_c作为深度/距离。 -
clamp防止 z c z_c zc 过小引起数值不稳(图右下角"齐次坐标→笛卡尔坐标/归一化平面"的步骤)。
到此为止,图中的 P ′ = K E P P' = KEP P′=KEP 基本就实现了:
u v 1 \] ∼ K \[ R t \] \[ x l y l z l 1 \] \\begin{bmatrix}u\\\\v\\\\1\\end{bmatrix} \\sim K \\begin{bmatrix}R \& t\\end{bmatrix} \\begin{bmatrix}x_l\\\\y_l\\\\z_l\\\\1\\end{bmatrix} uv1 ∼K\[Rt\] xlylzl1
(c) 图像增强(resize/crop/flip/rotate 等)的前向作用
python
cur_coords = cur_img_aug_matrix[:, :3, :3].matmul(cur_coords)
cur_coords += cur_img_aug_matrix[:, :3, 3].reshape(-1, 3, 1)
cur_coords = cur_coords[:, :2, :].transpose(1, 2) # -> (N_cam, N_pts, 2) 像素坐标
cur_coords = cur_coords[..., [1, 0]] # 交换为 (row, col) 顺序-
这一步把像素坐标 ( u , v ) (u,v) (u,v) 用
img_aug_matrix变换到增强后图像平面(图里没有画,但你在上一张图讲过 img 的仿射矩阵)。 -
随后调整坐标顺序以对齐后续索引:通常
[..., 0]表示 y(row) ,[..., 1]表示 x(col)。
(d)可见性判断与反填充深度图(splatting)
python
on_img = (
(cur_coords[..., 0] < H) & (cur_coords[..., 0] >= 0) &
(cur_coords[..., 1] < W) & (cur_coords[..., 1] >= 0)
)
for c in range(on_img.shape[0]): # 遍历相机
masked_coords = cur_coords[c, on_img[c]].long() # 落入图内的像素
masked_dist = dist[c, on_img[c]] # 对应 z_c
depth[b, c, 0, masked_coords[:, 0], masked_coords[:, 1]] = masked_dist-
只保留投影到图像内的点;对每个相机,把点的深度值
z_c写回到depth的像素位置。 -
这一步得到 per-camera 的稀疏深度图(与 BEVDepth/BEVFusion 思路一致)。
-
注意:如果多个点投到同一像素,这里是"最后一个覆盖",更稳妥的做法可用最近深度/最小化/加权统计(实现里可选)。
4️⃣ 计算体素几何:用于 BEV 体素化/池化
python
extra_rots = lidar_aug_matrix[..., :3, :3]
extra_trans = lidar_aug_matrix[..., :3, 3]
geom = self.get_geometry(
camera2lidar_rots, camera2lidar_trans,
intrins, post_rots, post_trans,
extra_rots=extra_rots, extra_trans=extra_trans,
)-
get_geometry(...)会用到:-
相机→LiDAR 外参:把每个像素的射线(由深度桶/离散深度)回投到 LiDAR/ego;
-
内参 K 与 post_rots/post_trans (图像增强)把特征平面上的像素格点反求到归一化平面上的射线方向;
-
extra_rots/trans 叠加 LiDAR 侧增强。
-
-
结果
geom往往是大小 ( B , N c a m , D , H ′ , W ′ , 3 ) (B, N_{cam}, D, H', W', 3) (B,Ncam,D,H′,W′,3) 的 3D 网格坐标(或体素索引),用于后续 bev_pool 把特征从相机体素体映射到 BEV 网格。
5️⃣ 把代码与公式逐式对齐
-
相机内参(图中蓝框 K)
intrins = cam_intrinsic[..., :3, :3] = K -
相机外参(图中橙框 E)
代码里两种形态:
-
lidar2image:直接给到 K [ R ∣ t ] K[R|t] K[R∣t](每相机一组),在循环里用; -
camera2lidar_rots/trans:传给get_geometry作反向回投。
-
-
透视除法与归一化平面(图右下角)
cur_coords[:, :2, :] /= cur_coords[:, 2:3, :]对应 ( x / z , y / z ) (x/z,\;y/z) (x/z,y/z)。 -
增强矩阵
-
图像侧
img_aug_matrix:对像素坐标的仿射(先前你讲的 resize/crop/flip/rotate 的合成矩阵); -
LiDAR 侧
lidar_aug_matrix:对 3D 点的刚体变换,使用其逆把点云还原,再将增强作为extra_*叠加到几何生成。
-
-
最终深度图
depth[b, cam, 0, y, x] = z_c:为每个相机/像素提供稀疏深度,供后面的体素化/体积融合(如深度概率或离散深度体)使用。
vtranform第二步将具有深度点云特征和图像特征进行融合
使用get_cam_feats
python
x = self.get_cam_feats(img, depth)
# image 大小为[1,6,256,32,88]
# depth 大小为[1,6,1,256,704] 为点云投影到图像上,具有深度信息具体函数定义如下:
python
@force_fp32()
def get_cam_feats(self, x, d): # x(1,6,156,32,88) d(1,6,1,256,704)
B, N, C, fH, fW = x.shape # 1,6,256,32,88
d = d.view(B * N, *d.shape[2:]) # 6,1,256,704
x = x.view(B * N, C, fH, fW) # 6,256,32,88
d = self.dtransform(d) # 结果6, 64, 32, 88
x = torch.cat([d, x], dim=1) # 6,320,32,88
x = self.depthnet(x) # 结果6,198,32,88
depth = x[:, :self.D].softmax(dim=1) # 6,118,32,88
x = depth.unsqueeze(1) * x[:, self.D:(self.D + self.C)].unsqueeze(2) # 6,80,118,32,88
x = x.view(B, N, self.C, self.D, fH, fW) # 1,6,80,118,32,88
x = x.permute(0, 1, 3, 4, 5, 2) # 1,6,118,32,88,80
return x🔁 dtransform 深度分支与特征融合流程
🟦 图像特征图 x
(1, 6, 256, 32, 88) 🟦 点云 points
(各相机采样、过滤) 🟦 映射到 6 个相机图像上,提取 depth
(1, 6, 1, 256, 704) 🟦 view(B*N, 256, 32, 88) 🟦 view(B*N, 1, 256, 704) 🟦 dtransform 深度转换网络得到 d
(6, 64, 32, 88) 🔶 concat 🟩 depthnet 得到 x
(6, 198, 32, 88) 🟥 前 118 维 softmax 🟨 output: depth
深度概率分布 (6, 118, 32, 88) 🔶 unsqueeze(1) 🔶 (与后 80 维特征)unsqueeze(2) 🔷 外积(构造体素/体积通道)
view & permute 🟨 output: x
(1, 6, 118, 32, 88, 80)
📦 张量形状速览
| 阶段 | 张量/操作 | 形状 |
|---|---|---|
| 输入 | 图像特征 x |
(1, 6, 256, 32, 88) |
| 输入 | 点云投影得到 depth |
(1, 6, 1, 256, 704) |
| 视图变换 | x -> view(B*N, 256, 32, 88) |
(B*N, 256, 32, 88) |
| 视图变换 | depth -> view(B*N, 1, 256, 704) |
(B*N, 1, 256, 704) |
| 深度分支 | dtransform 输出 d |
(6, 64, 32, 88) |
| 融合 | concat([x, d]) → depthnet 输出 |
(6, 198, 32, 88) |
| 概率 | 前 118 维 softmax → depth 概率 |
(6, 118, 32, 88) |
| 体积 | 取后 80 维,外积 & 整形 | (1, 6, 118, 32, 88, 80) |
vtranform第三步视锥转换
使用get_geometry函数
图像坐标系视锥点投影到 lidar 坐标系,得到视锥点云
-
其形状为:
(1, 6, 118, 32, 88, 3) -
含义为:
batch_size = 1,6 张32×88大小的 feature 图片。此 feature 上任意像素的点的深度有118个索引。只要知道正确的索引,就能知道这个索引对应在 lidar 坐标系的真实xyz坐标(米为单位,以 lidar 为坐标原点)。
BEV空间创建
python
def gen_dx_bx(xbound, ybound, zbound):
dx = torch.Tensor([row[2] for row in [xbound, ybound, zbound]])
bx = torch.Tensor([row[0] + row[2] / 2.0 for row in [xbound, ybound, zbound]])
nx = torch.LongTensor(
[(row[1] - row[0]) / row[2] for row in [xbound, ybound, zbound]]
)
return dx, bx, nx把给定的空间边界描述 [min, max, step](分别对应 x、y、z 三个轴)转换成三样东西:
-
dx:每个轴上的网格步长(cell 大小) -
bx:每个轴上第一个网格中心 的位置(=min + step/2) -
nx:每个轴上的网格数量(=(max - min) / step,整型)
变量解释
-
dx: 取每个轴的第三个元素step,得到[dx, dy, dz]。 -
bx: 取每个轴的min + step/2,这是把网格定义为以中心对齐(center-aligned),第一个 cell 的中心在这里。 -
nx: 计算每个轴的 cell 个数(max - min) / step,并转成长整型。
ini
xbound = [-54.0, 54.0, 0.3]
ybound = [-54.0, 54.0, 0.3]
zbound = [-10.0, 10.0, 20.0]计算结果:
-
dx = [0.3, 0.3, 20.0] -
bx = [-54 + 0.15, -54 + 0.15, -10 + 10] = [-53.85, -53.85, 0.0] -
nx = [ (108/0.3), (108/0.3), (20/20) ] = [360, 360, 1 ]
视锥创建
create_frustum 的函数,是在图像坐标系 里为每个 feature 像素位置生成一条"深度采样射线"的三维网格 (u, v, d),也就是视锥体体素 (frustum grid)。后续会用相机内参把这些 (u,v,d) 投到相机/激光雷达坐标系得到 3D 点。
python
@force_fp32()
def create_frustum(self):
iH, iW = self.image_size # 原始输入图片的高宽 (H, W)
fH, fW = self.feature_size # 下采样后的特征图尺寸 (H', W')
# 深度采样:dbound = [d_min, d_max, d_step]
ds = (torch.arange(*self.dbound, dtype=torch.float)
.view(-1, 1, 1) # 形状 (D, 1, 1)
.expand(-1, fH, fW)) # 复制到 (D, fH, fW)
D, _, _ = ds.shape # 深度采样数 D = floor((d_max-d_min)/d_step)
# x 像素坐标(横向):从 0 到 iW-1,均匀取 fW 个采样点,再复制到 (D, fH, fW)
xs = (torch.linspace(0, iW - 1, fW, dtype=torch.float)
.view(1, 1, fW) # (1, 1, fW)
.expand(D, fH, fW)) # (D, fH, fW)
# y 像素坐标(纵向):从 0 到 iH-1,均匀取 fH 个采样点,再复制到 (D, fH, fW)
ys = (torch.linspace(0, iH - 1, fH, dtype=torch.float)
.view(1, fH, 1) # (1, fH, 1)
.expand(D, fH, fW)) # (D, fH, fW)
# 堆成最后一维为 3 的张量:(D, fH, fW, 3),每个位置是 [u, v, d]
frustum = torch.stack((xs, ys, ds), -1)
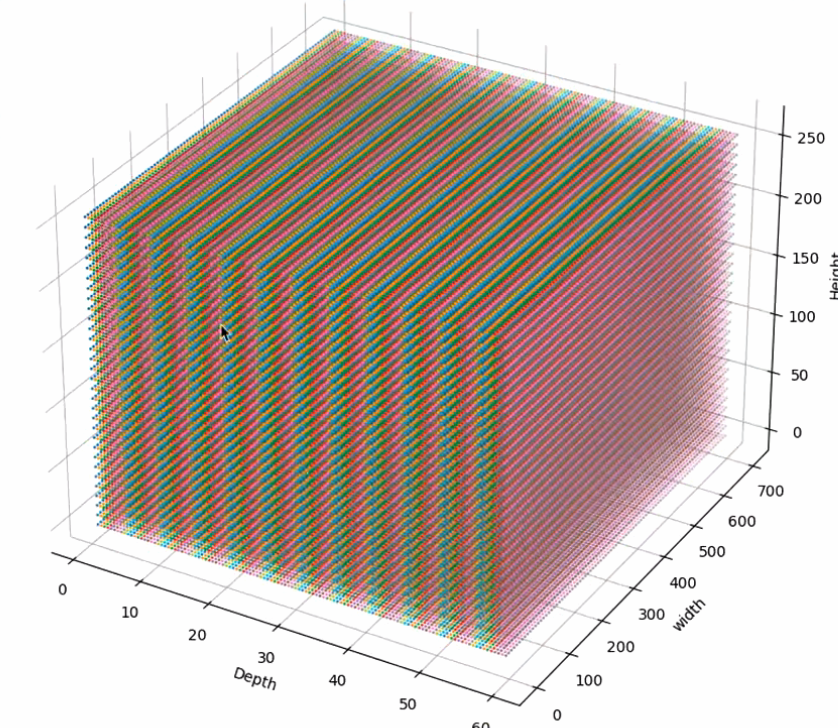
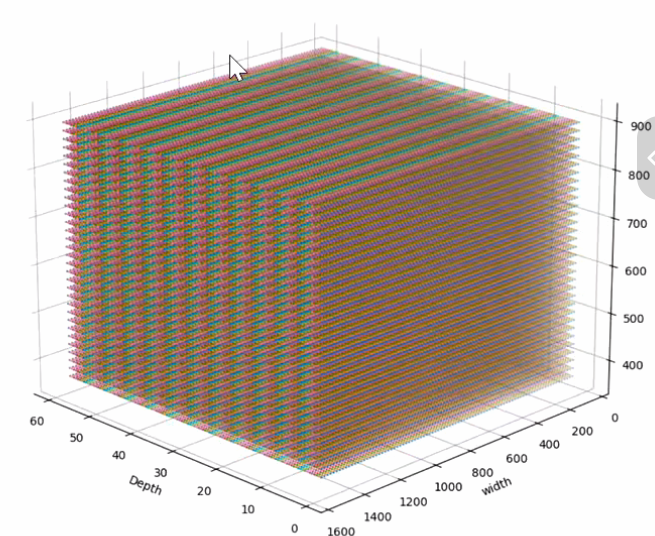
return nn.Parameter(frustum, requires_grad=False)关键点说明
-
dbound:例如[1.0, 60.0, 0.5],则D = (60-1)/0.5 = 118,与你截图中的ds.shape = [118, 32, 88]一致。 -
xs/ys的取值 :并不是直接用特征图的 0...fW-1 / 0...fH-1,而是把它们映射回原图像素坐标 范围0..iW-1、0..iH-1,相当于隐含了下采样步长(iW/fW,iH/fH)。 -
形状 :最终
frustum的形状是(D, fH, fW, 3),每个体素里存放一个(u, v, d)。后面用相机内参K做反投影:X Y Z \] = d ⋅ K − 1 \[ u v 1 \] \\begin{bmatrix}X\\\\Y\\\\Z\\end{bmatrix} = d \\cdot K\^{-1}\\begin{bmatrix}u\\\\v\\\\1\\end{bmatrix} XYZ =d⋅K−1 uv1 再配合外参可变换到 ego/lidar 坐标系。
-
返回值类型 :用
nn.Parameter(..., requires_grad=False)保存为不可训练参数 (常量),会随模型.to(device)、.state_dict()一起移动/保存。很多实现也会用register_buffer来表达"常量缓冲"。
相平面到激光雷达坐标系
get_geometry 代码中的变换步骤:
1. 后处理旋转和平移(undo post-transformation)
python
points = self.frustum - post_trans.view(B, N, 1, 1, 1, 3)
points = torch.inverse(post_rots).view(B, N, 1, 1, 1, 3, 3).matmul(points.unsqueeze(-1))-
self.frustum是原始的视锥体,形状为 ( D , H ′ , W ′ , 3 ) (D, H', W', 3) (D,H′,W′,3),包含了每个像素位置的 ( u , v , d ) (u, v, d) (u,v,d),其中 u u u 和 v v v 是像素坐标, d d d 是深度值。 -
post_trans是一个平移向量,表示对视锥体的平移。我们用它从frustum中减去,表示"撤销"视锥体上的平移操作:p o i n t s = f r u s t u m − p o s t _ t r a n s \mathbf{points} = \mathbf{frustum} - \mathbf{post\_trans} points=frustum−post_trans
-
post_rots是旋转矩阵,表示对视锥体进行旋转。首先计算post_rots的逆矩阵 R − 1 R^{-1} R−1,然后用它对视锥体进行旋转变换:p o i n t s = R − 1 ⋅ p o i n t s \mathbf{points} = R^{-1} \cdot \mathbf{points} points=R−1⋅points
其中 R − 1 R^{-1} R−1 是旋转矩阵,
matmul就是矩阵乘法操作。对矩阵进行逆向增广,将原来图像的
704*256还原到1600*900
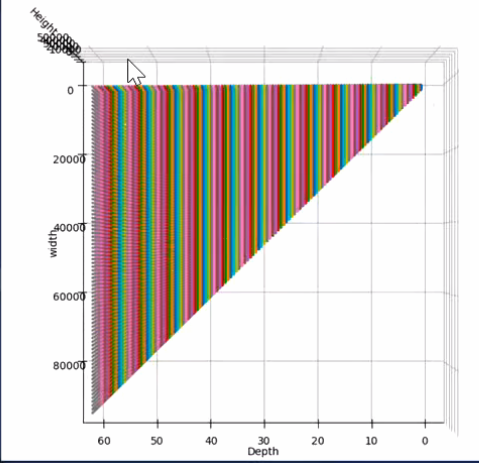
2. 深度缩放操作
python
points = torch.cat((
points[:, :, :, :, :, :2] * points[:, :, :, :, :, 2:3],
points[:, :, :, :, :, 2:3],
), 5)- 我们将 ( u , v ) (u, v) (u,v) 坐标和深度值 d d d 结合起来,得到实际的 3D 空间中的坐标。由于 u u u 和 v v v 是在图像坐标系中,深度值 d d d 表示该点在视锥体中的深度。我们将 u u u 和 v v v 坐标按照深度 d d d 缩放,得到它们在三维空间中的真实坐标。
X = [ u ⋅ d , v ⋅ d , d ] \mathbf{X} = \left[ u \cdot d, \quad v \cdot d, \quad d \right] X=[u⋅d,v⋅d,d]
其中 u ⋅ d u \cdot d u⋅d 和 v ⋅ d v \cdot d v⋅d 是对像素坐标的深度缩放。
3. 相机到激光雷达坐标系转换
python
combine = camera2lidar_rots.matmul(torch.inverse(intrins))
points = combine.view(B, N, 1, 1, 1, 3, 3).matmul(points).squeeze(-1)
points += camera2lidar_trans.view(B, N, 1, 1, 1, 3)camera2lidar_rots是从相机坐标系到激光雷达坐标系的旋转矩阵,intrins是相机的内参矩阵。首先,我们通过计算 R lidar = R camera ⋅ R intrins − 1 R_{\text{lidar}} = R_{\text{camera}} \cdot R_{\text{intrins}}^{-1} Rlidar=Rcamera⋅Rintrins−1,得到一个旋转矩阵,用来将相机坐标系的点转换到激光雷达坐标系。
R lidar = R camera ⋅ R intrins − 1 R_{\text{lidar}} = R_{\text{camera}} \cdot R_{\text{intrins}}^{-1} Rlidar=Rcamera⋅Rintrins−1
- 然后,将每个点的坐标与这个旋转矩阵相乘,得到激光雷达坐标系下的点:
p o i n t s lidar = R lidar ⋅ p o i n t s \mathbf{points}{\text{lidar}} = R{\text{lidar}} \cdot \mathbf{points} pointslidar=Rlidar⋅points
- 最后,加上从相机坐标系到激光雷达坐标系的平移变换 T lidar T_{\text{lidar}} Tlidar,得到最终的激光雷达坐标系下的点坐标:
p o i n t s final = p o i n t s lidar + T lidar \mathbf{points}{\text{final}} = \mathbf{points}{\text{lidar}} + T_{\text{lidar}} pointsfinal=pointslidar+Tlidar
4. 额外的旋转和平移变换(可选)
python
if "extra_rots" in kwargs:
extra_rots = kwargs["extra_rots"]
points = (
extra_rots.view(B, 1, 1, 1, 1, 3, 3)
.repeat(1, N, 1, 1, 1, 1, 1)
.matmul(points.unsqueeze(-1))
.squeeze(-1)
)- 如果
kwargs中存在额外的旋转矩阵extra_rots,我们会再对当前的点进行一次旋转变换:
p o i n t s final = R extra ⋅ p o i n t s final \mathbf{points}{\text{final}} = R{\text{extra}} \cdot \mathbf{points}_{\text{final}} pointsfinal=Rextra⋅pointsfinal
5. 额外的平移变换(可选)
python
if "extra_trans" in kwargs:
extra_trans = kwargs["extra_trans"]
points += extra_trans.view(B, 1, 1, 1, 1, 3).repeat(1, N, 1, 1, 1, 1)- 如果
kwargs中存在额外的平移矩阵extra_trans,我们会在旋转之后再对点进行平移变换:
p o i n t s final = p o i n t s final + T extra \mathbf{points}{\text{final}} = \mathbf{points}{\text{final}} + T_{\text{extra}} pointsfinal=pointsfinal+Textra
总结
get_geometry 的目标是将每个像素的视锥体点从原始图像坐标系转换到激光雷达坐标系中,涉及多个变换步骤:
-
撤销后处理的平移和旋转:先对视锥体进行平移和旋转。
-
深度缩放 :将每个像素的 u u u, v v v 坐标与深度值 d d d 相结合,得到实际的 3D 坐标。
-
从相机坐标系到激光雷达坐标系的转换:通过旋转矩阵和内参矩阵进行变换,得到激光雷达坐标系下的点。
-
额外的变换:根据输入的额外旋转和平移矩阵,对点进行二次变换。