文章目录
-
- [1. 引言:误差不可避免,但可被理解](#1. 引言:误差不可避免,但可被理解)
- [2. 模型误差的三类来源(The Three Sources of Error)](#2. 模型误差的三类来源(The Three Sources of Error))
-
- [2.1 Noise:数据固有的"噪声"](#2.1 Noise:数据固有的"噪声")
- [2.2 Model-Bias:模型结构固有的"偏差"](#2.2 Model-Bias:模型结构固有的"偏差")
- [2.3 Variance:数据不足导致的"方差"](#2.3 Variance:数据不足导致的"方差")
- [3. 偏差-方差权衡(The Bias-Variance Tradeoff)](#3. 偏差-方差权衡(The Bias-Variance Tradeoff))
-
- [3.1 数学本质:泛化误差的分解](#3.1 数学本质:泛化误差的分解)
- [3.2 核心权衡:模型复杂度的双重效应](#3.2 核心权衡:模型复杂度的双重效应)
- [4. 演进过程](#4. 演进过程)
- [5. 实践指南:如何诊断与优化?](#5. 实践指南:如何诊断与优化?)
- [6. 总结](#6. 总结)
为何模型在训练集上无法达到满分?为何在测试集上表现会下降?本文将从第一性原理出发,为你彻底讲透模型误差的来源与权衡之道。
1. 引言:误差不可避免,但可被理解
在机器学习项目中,追求一个"完美"的模型是常见的目标。但一个关键且反直觉的事实是:一个在训练集上表现过于完美的模型,往往在新数据上会表现糟糕。
这引出了核心问题:模型的误差从何而来?哪些可以避免,哪些必须接受? 理解这一点,是迈向优秀机器学习实践者的第一步。本文将结合经典理论与实例,对模型误差进行一层层的深度剖析。
2. 模型误差的三类来源(The Three Sources of Error)
根据MIT论文《Neural Networks and the Bias/Variance Dilemma》的论述,模型的误差通常可归结为以下三个基本类别。这种划分是我们理解所有问题的基石。
模型总误差 Noise
数据固有噪声 Model-Bias
模型固有偏差 Variance
数据不足导致的方差 不可消除 可通过改变
模型结构降低 可通过
增加数据降低
2.1 Noise:数据固有的"噪声"
- 本质 :这是存在于客观环境和标签本身的随机波动,与模型好坏无关。它衡量了"真实期望"与"观测标签"之间的差距。
- 关键洞察 :Noise是不可消除的误差,它构成了模型预测精度的理论下限。
- 生动举例 :
- 一个文档的真实点击概率是0.2。但你拿到手的训练数据是二元的(0或1),表现为
[0, 0, 1, 0, 0, ...]的序列。即使你的模型完美地预测出了0.2的概率,其预测与单个样本的标签之间依然存在误差(如0 - 0.2或1 - 0.2)。这就是Noise。 - 专家标注的一致性也不是100%。对于同一个样本,可能80%的专家标为1,20%的专家标为0。这种不一致性也是Noise。
- 一个文档的真实点击概率是0.2。但你拿到手的训练数据是二元的(0或1),表现为
2.2 Model-Bias:模型结构固有的"偏差"
- 本质 :这是由于模型结构本身的学习能力局限所带来的系统性误差。即使你的数据覆盖了全部特征空间且数据量无限,这个误差依然存在。
- 关键洞察 :Bias是模型自身的"天花板"。一个简单的模型(如线性回归)天生就无法拟合一个高度复杂的真实规律(如正弦曲线)。
- 简单理解:就像你用一把直尺(简单模型)去测量一个弯曲瓶子的周长,无论你测量得多仔细(数据再多),直尺这种工具本身注定会带来系统性的偏差。
2.3 Variance:数据不足导致的"方差"
- 本质 :这是由于训练数据量有限,导致模型过于敏感地学习了当前训练集特有的随机噪声和非全局模式,而非底层规律。
- 关键洞察 :Variance是"过拟合"的根源 。它代表了模型的不稳定性。通过增加高质量数据,Variance可以被有效降低。
- 简单理解:一个学生为了通过考试,不是去理解核心概念(底层规律),而是死记硬背了某本习题集里的所有题目和答案(训练数据中的噪声)。如果考试题(测试数据)稍有变化,他就可能考砸。不同的习题集(不同的训练集)会让他背出完全不同的答案(模型预测波动大)。
3. 偏差-方差权衡(The Bias-Variance Tradeoff)
上述三类误差中,Noise是不可控的 。因此,我们优化的焦点就落在了如何平衡 Model-Bias 和 Variance 上。这就引出了机器学习的核心矛盾------偏差-方差权衡。
3.1 数学本质:泛化误差的分解
通过数学推导,回归问题的期望泛化误差可被精确分解为:
E [ ( y − y ^ ) 2 ] = Bias ( y ^ ) 2 + Var ( y ^ ) + σ 2 E[(y - \hat{y})^2] = \text{Bias}(\hat{y})^2 + \text{Var}(\hat{y}) + \sigma^2 E[(y−y^)2]=Bias(y^)2+Var(y^)+σ2
- Bias ( y ^ ) 2 \text{Bias}(\hat{y})^2 Bias(y^)2:即上述 Model-Bias 的平方。
- Var ( y ^ ) \text{Var}(\hat{y}) Var(y^):即上述 Variance。
- σ 2 \sigma^2 σ2:即上述 Noise。
这个公式从第一性原理证明,我们的总误差来源于这三个根本不同的部分。
3.2 核心权衡:模型复杂度的双重效应
模型复杂度是控制这个权衡的"旋钮",但它对Bias和Variance的影响是相反的:
-
降低模型复杂度(如使用线性模型):
- Bias升高 :模型不够灵活,无法捕捉真实规律,导致欠拟合。
- Variance降低:模型简单稳定,对不同数据集的敏感度低。
-
增加模型复杂度(如使用深度神经网络):
- Bias降低:模型足够强大,可以很好地拟合训练数据中的真实规律。
- Variance升高 :模型过于灵活,开始"记忆"训练数据中的噪声,导致过拟合,模型变得不稳定。
下图直观展示了这一关键权衡关系:
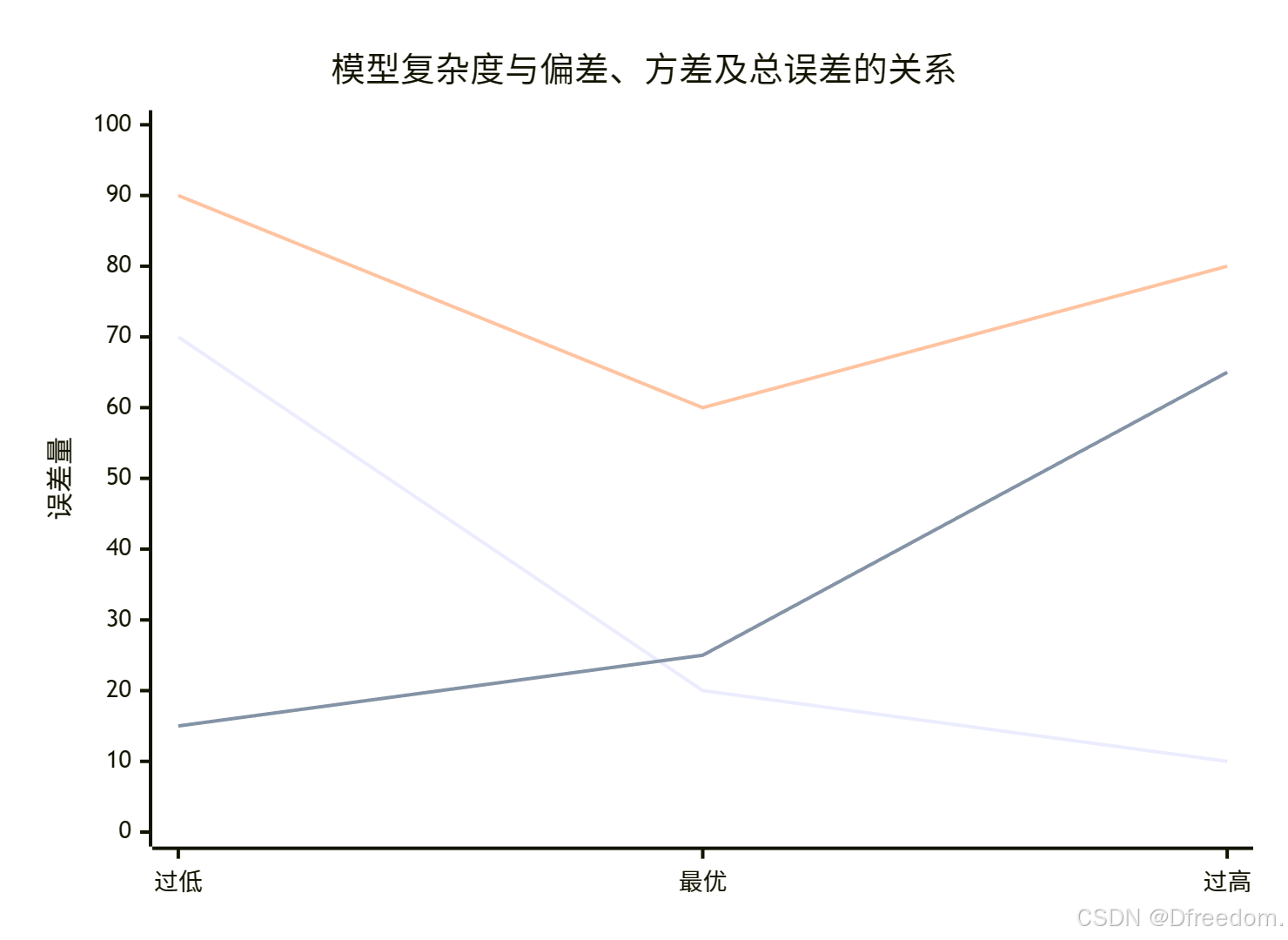
我们的目标,就是找到上图中总误差曲线的最低点,即模型复杂度的"最佳点"。
4. 演进过程
该理论的发展及其应对策略的演进,可以概括为以下图谱:
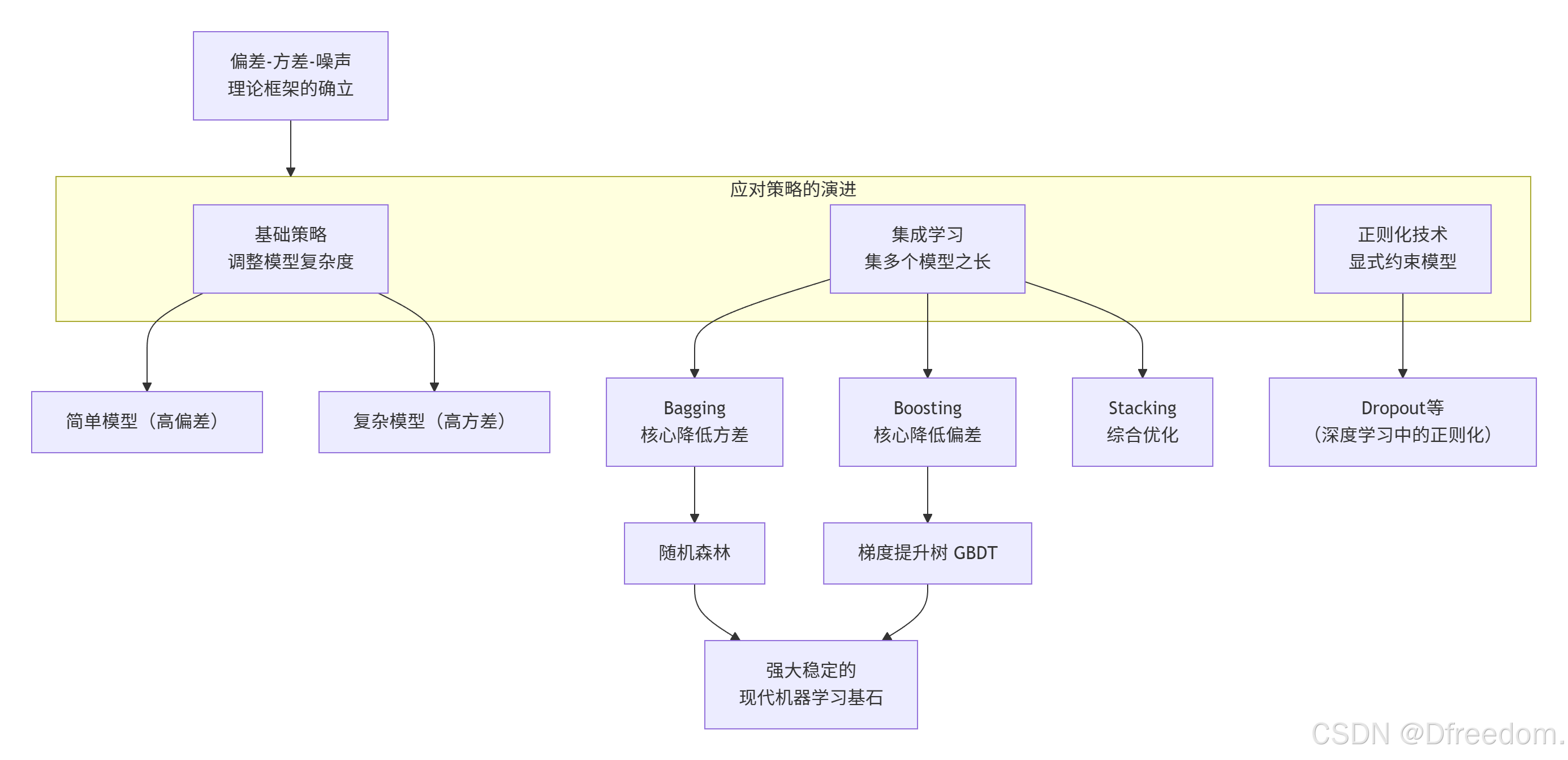
5. 实践指南:如何诊断与优化?
理论的价值在于指导实践。以下是应对偏差-方差问题的系统性流程:
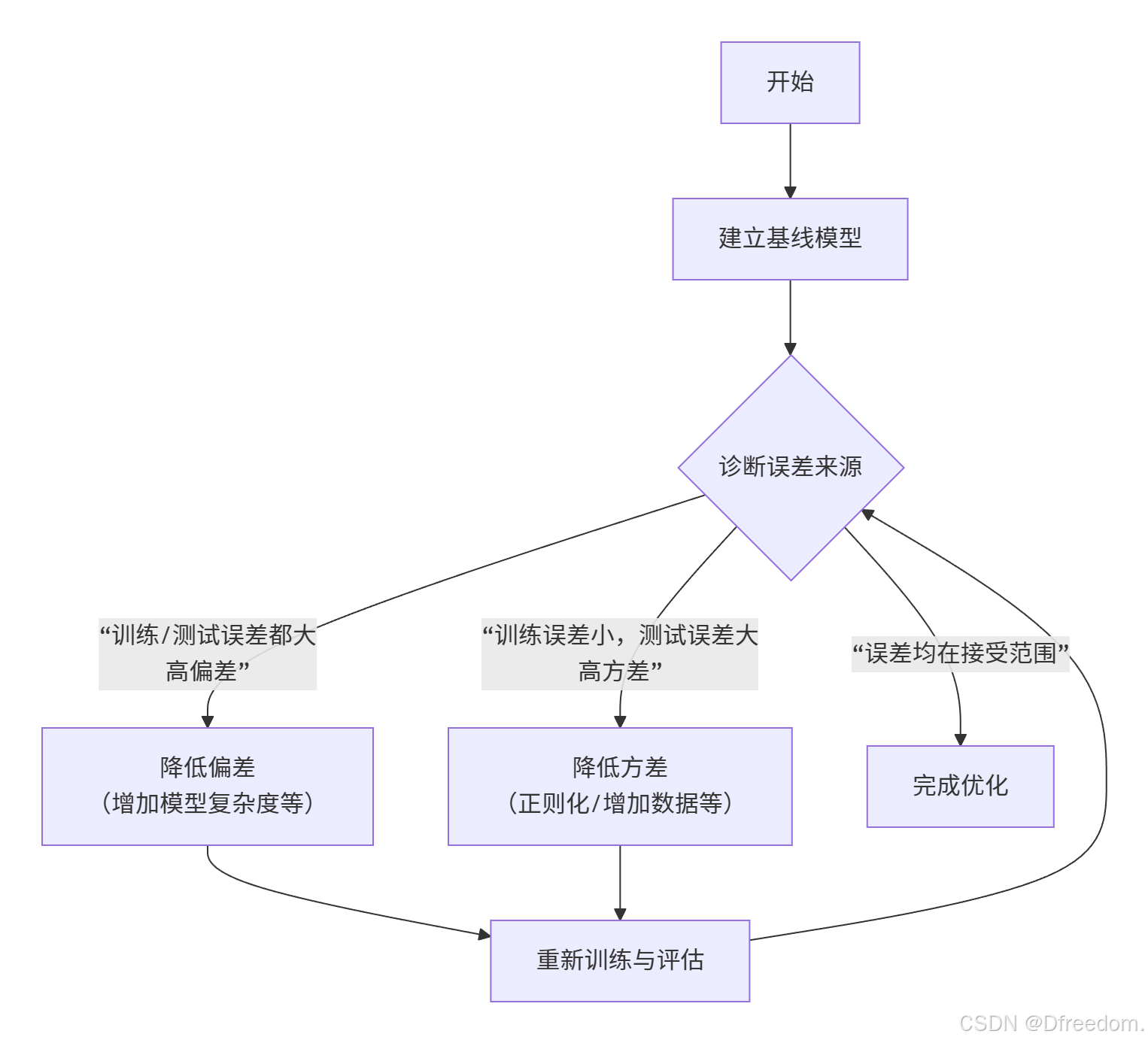
巧妙之处:这个框架告诉我们,优化模型不是盲目地"调参",而是要先诊断误差的主要矛盾,然后进行针对性干预。
诊断与策略对照表
| 现象 | 诊断 | 优化策略 |
|---|---|---|
| 训练误差高,验证误差同样高 | 高偏差(欠拟合) | • 增加模型复杂度 (如从线性到非线性) • 增加更多有效特征 • 减少正则化强度 |
| 训练误差很低,但验证误差很高 | 高方差(过拟合) | • 获取更多训练数据 (最有效) • 增强正则化 (L2, Dropout) • 降低模型复杂度 • 使用集成方法(如Bagging) |
| 训练与验证误差都足够低且接近 | 达到良好平衡 | 模型表现良好,无需大幅调整 |
6. 总结
- 接受噪声(Noise):认识到数据中存在不可消除的随机波动,这是我们的预测精度的理论极限。
- 理解偏差(Bias):它是模型固有的系统性误差,需要通过选择合适的模型结构来降低。
- 控制方差(Variance):它源于数据不足,需要通过增加数据、正则化等方法来抑制。
- 寻求权衡(Trade-off):机器学习的艺术,就在于找到模型复杂度的最佳点,使偏差和方差之和最小化,从而获得最佳的泛化能力。