算法闯关日记 Episode ：解锁链表「环形」迷局与「相交」奥秘

文章目录

引言
一、环形链表
- [1.1 思路解答 + 作图演示](#1.1 思路解答 + 作图演示)
- [1.2 算法验证](#1.2 算法验证)
二、环形链表Ⅱ
- [2.1 算法解答 + 作图演示](#2.1 算法解答 + 作图演示)
- [2.2 算法验证](#2.2 算法验证)
总结

引言

在链表的算法世界里，「环形」结构是一个经典且有趣的谜题。当链表的尾指针并非指向空，而是指向链表中某个先前的节点时，一个环便悄然形成。

本期，我们将聚焦于环形链表的两大核心问题：如何判断链表中是否存在环？以及，如果存在环，如何准确地找到环的起点？

一、环形链表

题目链接：141.环形链表(LeetCode)

题目描述：

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。

（为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。）

实现示例：

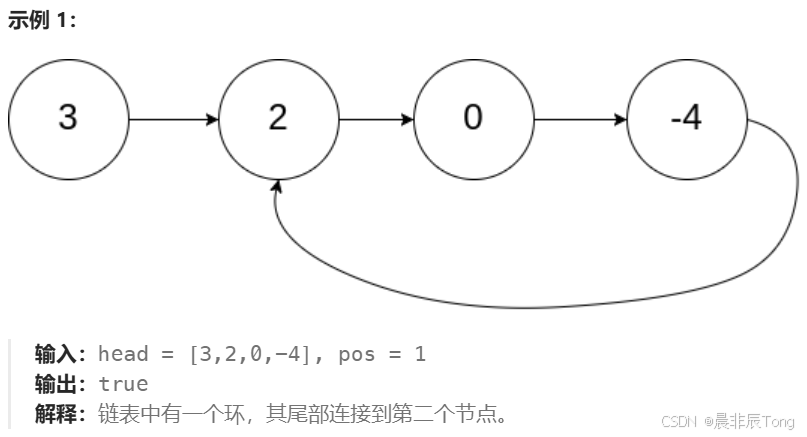
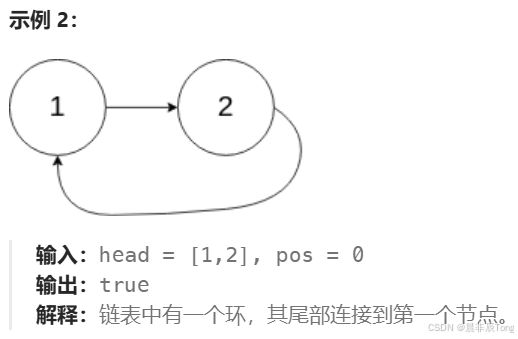
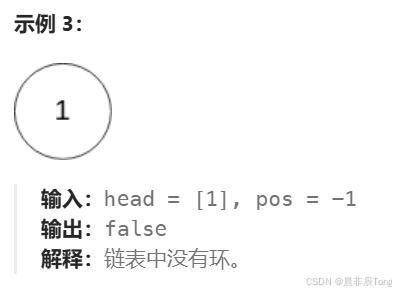
1.1 思路解答 + 作图演示

算法思路：
简单来看，就是判断链表的尾节点不为空(NULL)。那么该如何操作呢？

上一篇博客提到的方法，将链表转换为数组，再进行操作。对于这个算法题来说，转换为数组后在数组内部遍历比较。（有条件限制，废弃）

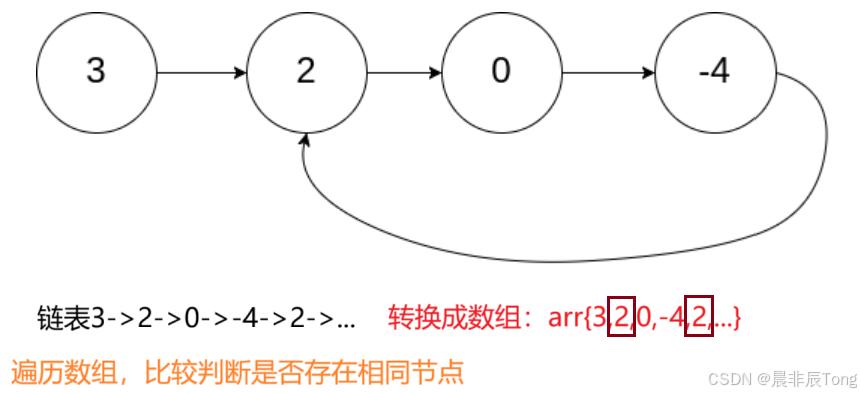
经过作图，此方法将链表转换为数组后再判断确实可以。但是别忘了一个重要的前提，题目要给出链表的最大长度！！ （上一篇博客中提到：回文链表）

可惜，看完题目要求，没有给出相关条件，那么不能用这个方法！
使用快慢指针，慢指针走1步，快指针走2步，看是否指针会相遇。

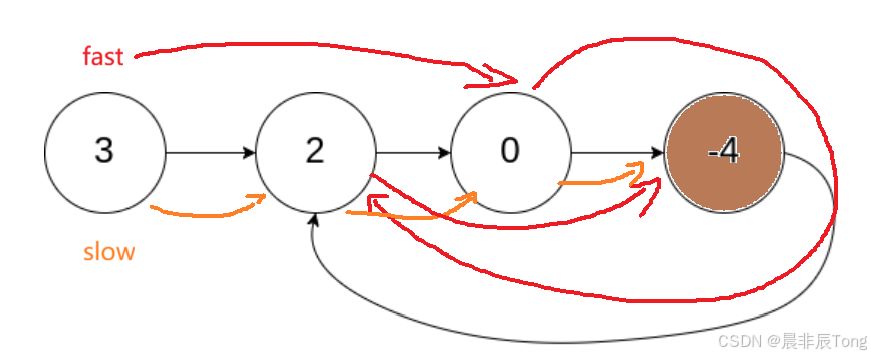
经过作图，最终快慢指针在节点数值为4的地方相遇，表示链表为环形链表。

1.2 算法验证

验证思路2：使用快慢指针，观察指针是否会相遇。

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
 typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) 
{
    //定义快慢指针
    ListNode* fast = head;
    ListNode* slow = head;

    //循环，开始追赶
    while(fast && fast->next)
    {
        //慢走1步，快走2步
        slow = slow->next;
        fast = fast->next->next;

        if(fast == slow)
        {
            return true;
        }
    }

    //循环外，没有相遇
    return false;
}

验证思路合理性

证明1：在环形链表中，慢指针走1步，快指针走2步，最终一定会相遇？为什么？

先说答案：一定会相遇！

要明确：快指针比慢指针先进入环形部分 。假设两个指针之间的距离差值为N，那么移动后就是N+1-2 = N-1，反复进行，也就是说每次距离差值缩小1位。这就好说了，不管N有多大，只要-1-1-1......最终都会归0，也就是相遇。

证明2：在环形链表中，慢指针走1步，快指针走2、3、4......步，还会相遇吗？

那可就不一定相遇了！！

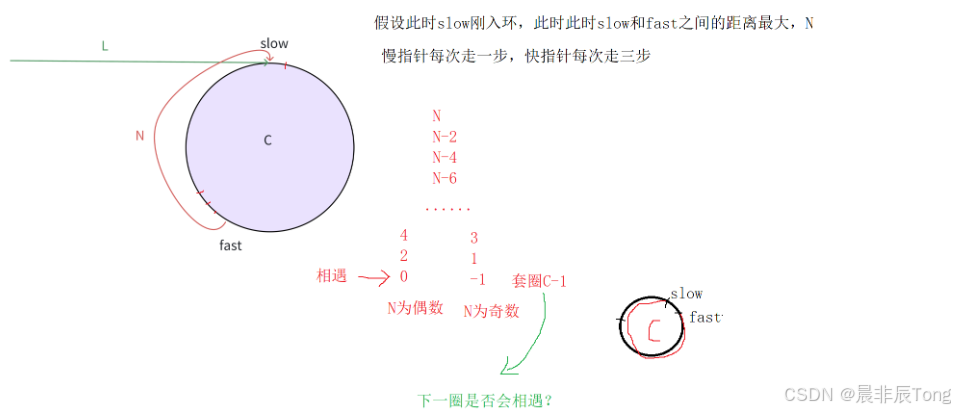
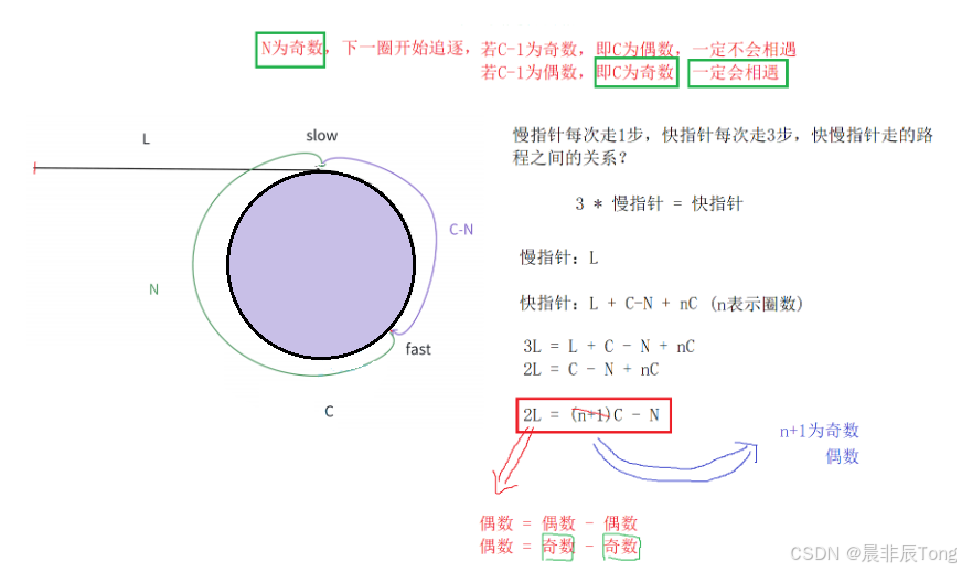
经过上面的一系列证明，得出：在以后的算法使用快慢指针时，还是慢指针走1步、快指针走2步比较稳妥！

二、环形链表Ⅱ

题目链接：142.环形链表Ⅱ(LeetCode)

题目描述：

给定一个链表的头节点 head ，返回链表开始入环的第一个节点 。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。

（为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不能改变链表结构！）

实现示例：
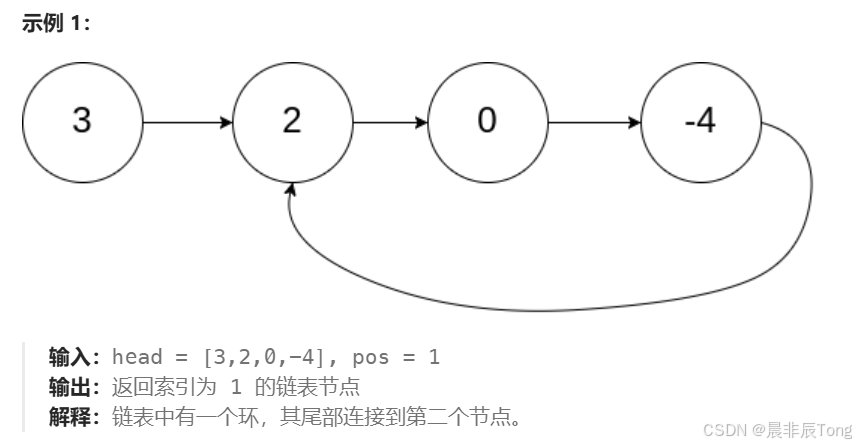
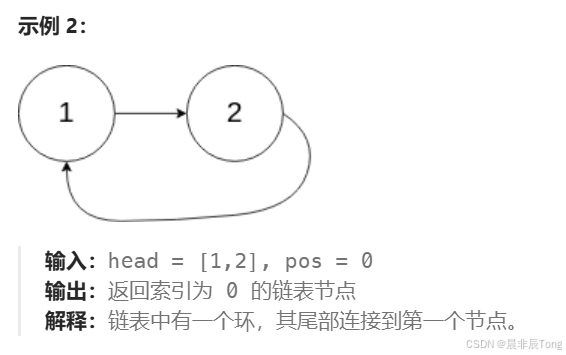
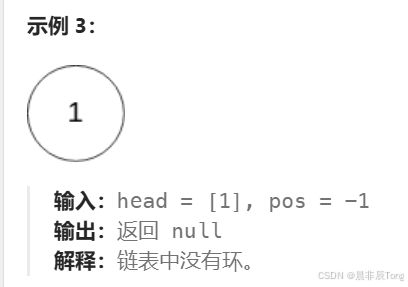
题目提示：

链表中节点的数目范围在范围 [0, 10⁴] 内；
-105 <= Node,val <= 105；
pos 的值为 -1 或者链表中的一个有效索引；

2.1 算法解答 + 作图演示

算法思路：

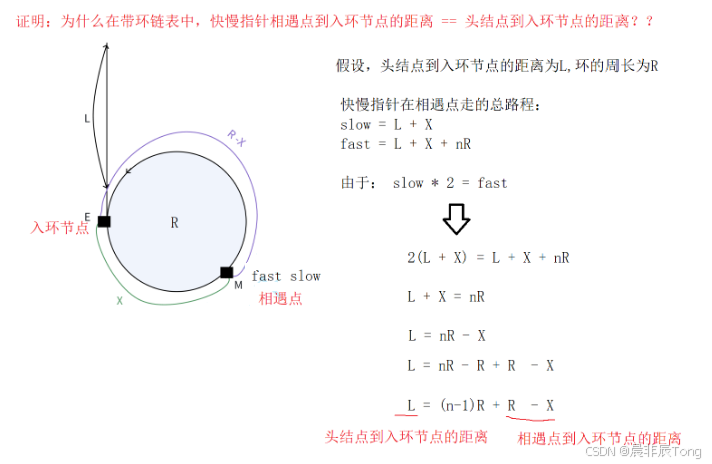
先利用快慢指针找出相遇的节点，再根据"头节点到入环节点的具体 = 相遇节点到入环节点的距离 "，定义一个节点从头节点开始移动，慢指针/快指针从相遇节点移动，等到新节点和慢指针相遇，所处位置就是入环节点的位置。

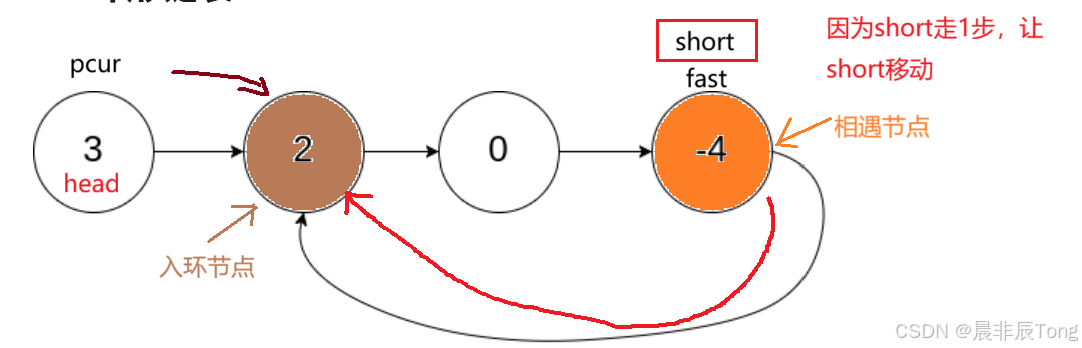
借用上一题的思路，找到相遇节点（-4）后，再新定义新节点pcur指向头节点，依据距离关系的推理（后面有验证），让pcur,short同步移动直到二者相遇，此为入环节点（2）。

2.2 算法验证

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
typedef struct ListNode ListNode;
struct ListNode* detectCycle(struct ListNode* head) 
{
    //创建快慢指针
    ListNode* slow = head;
    ListNode* fast = head;

    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;

        if (slow == fast)
        {
            //相遇节点--找入环节点
            ListNode* pcur = head;
            while (pcur != slow)
            {
                pcur = pcur->next;
                slow = slow->next;
            }
            return pcur;
        }
    }
    return NULL;
}

验证思路合理性：

总结

html 复制代码

🍓 我是晨非辰Tong！若这篇技术干货帮你打通了学习中的卡点：
👀 【关注】跟我一起深耕技术领域，从基础到进阶，见证每一次成长
❤️ 【点赞】让优质内容被更多人看见，让知识传递更有力量
⭐ 【收藏】把核心知识点、实战技巧存好，需要时直接查、随时用
💬 【评论】分享你的经验或疑问（比如曾踩过的技术坑？），一起交流避坑
🗳️ 【投票】用你的选择助力社区内容方向，告诉大家哪个技术点最该重点拆解
技术之路难免有困惑，但同行的人会让前进更有方向～愿我们都能在自己专注的领域里，一步步靠近心中的技术目标！

结语：

环检测：快指针（步长2）与慢指针（步长1）若相遇，则证明链表存在环。该方法时间复杂度为O(n)，空间复杂度为O(1)，实现最优效率。

入口定位：基于"头节点到入口距离等于相遇点到入口距离"的原理，分别从头部和相遇点出发同步移动，相遇处即为环入口。

算法价值：快慢指针法提供了解决环形链表的完整方案，从检测到定位形成系统方法论，是处理链表问题的核心技巧。