汽车角雷达波形设计与速度模糊解决方法研究
Liu, Y.; Zhang, D.; Wang, S.; Liu, J. A Waveform and Velocity Ambiguity Resolution Method for Corner Radar. Appl. Sci. 2024, 14, 5477. https://doi.org/10.3390/app14135477
1. 引言与研究背景
随着自动驾驶技术的快速发展,毫米波雷达系统正在经历从传统3D测量向4D测量的重要转型。这种演进的核心在于增加了俯仰角测量能力,从而为车辆提供更加全面的环境感知信息。在复杂多变的驾驶环境中,汽车毫米波雷达必须快速准确地提供车辆和行人的距离、速度和方位等关键信息,这对毫米波雷达技术提出了严格的要求。
与前向汽车雷达不同,角雷达在功能定位上有其独特性------它特别关注近距离目标的精确检测。角雷达主要服务于检测车辆侧面和斜前方区域,为变道辅助、盲点检测和泊车辅助等功能提供支持。基于这些特殊需求,本研究提出了一种创新的复合波形设计方案,专门针对配备四个发射器和四个接收器的汽车角雷达系统。
该方案的核心思想是采用不同的波形配置来适应不同的距离范围。通过这种自适应的波形策略,毫米波角雷达能够在近距(0-60米)和中距(60-100米)范围内实现更优越的距离分辨率和速度分辨率。然而,提高速度分辨率不可避免地会导致最大无模糊速度的降低,这是雷达系统设计中的一个基本权衡。为解决这一矛盾,本文提出了一种基于前后帧目标参数匹配的速度模糊解决方法。
2. FMCW雷达理论基础与数学模型
2.1 FMCW信号模型
在分析FMCW雷达系统时,我们假设雷达处于静止状态,而目标以速度vvv向雷达运动。图1展示了发射信号和接收信号之间的时频关系。
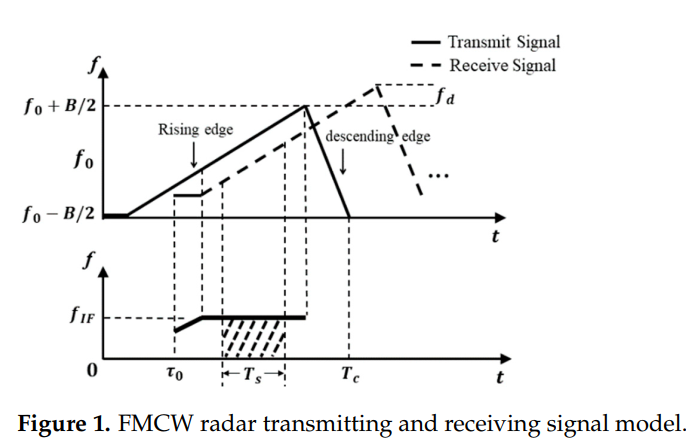
图1描述 :该图展示了FMCW雷达的发射信号(实线)和接收信号(虚线)在时频域的关系。横轴表示时间ttt,纵轴表示频率fff。发射信号从初始频率f0−B/2f_0 - B/2f0−B/2线性扫频至f0+B/2f_0 + B/2f0+B/2,形成锯齿波形状。接收信号由于目标距离产生时延τ0\tau_0τ0,同时由于目标运动产生多普勒频移fdf_dfd。图中清晰标注了上升沿时间TuT_uTu、下降沿时间TsT_sTs和完整的调频周期TcT_cTc。
系统的关键参数包括:调频带宽BBB定义了频率扫描的范围;调频周期TcT_cTc决定了单个完整扫频的时间;中心频率f0f_0f0是雷达工作的载波频率(通常为76.5 GHz或77 GHz);回波时延τ0=2r/c\tau_0 = 2r/cτ0=2r/c,其中rrr是目标距离,ccc是光速;多普勒频率fd=2vf0/cf_d = 2vf_0/cfd=2vf0/c反映了目标的径向速度;采样时长TsT_sTs决定了ADC采样窗口。
调频斜率定义为:
μ=BTu\mu = \frac{B}{T_u}μ=TuB
其中TuT_uTu表示频率上升沿时间。接收信号与发射信号经过混频器和低通滤波器处理后,得到中频信号:
fIF=2μrc−2vf0c=μτ0−fdf_{IF} = \frac{2\mu r}{c} - \frac{2vf_0}{c} = \mu\tau_0 - f_dfIF=c2μr−c2vf0=μτ0−fd
这个中频信号包含了目标的距离信息(通过μτ0\mu\tau_0μτ0项)和速度信息(通过fdf_dfd项)。
2.2 速度模糊现象的数学描述
脉冲重复频率定义为PRF=1/TcPRF = 1/T_cPRF=1/Tc,FFT的输入采样频率为FDF_DFD。根据奈奎斯特采样定理,多普勒频率fdf_dfd的无模糊范围为[−FD/2,FD/2][-F_D/2, F_D/2][−FD/2,FD/2]。当目标的实际速度产生的多普勒频率超出此范围时,会发生频谱折叠,导致速度模糊。
模糊后的多普勒频率可表示为:
fD=fd+k⋅1Tc=fd+k⋅FDf_D = f_d + k \cdot \frac{1}{T_c} = f_d + k \cdot F_DfD=fd+k⋅Tc1=fd+k⋅FD
其中k∈Zk \in \mathbb{Z}k∈Z是模糊倍数,fd∈[−FD/2,FD/2]f_d \in [-F_D/2, F_D/2]fd∈[−FD/2,FD/2]是折叠后观测到的多普勒频率。
2.3 雷达性能参数关系
雷达系统的主要性能参数之间存在密切的相互关系。距离分辨率由带宽决定:
ΔR=c2B\Delta R = \frac{c}{2B}ΔR=2Bc
最大无模糊距离取决于距离FFT点数:
Rmax=ΔR⋅NrFFT=c⋅NrFFT2BR_{max} = \Delta R \cdot N_{rFFT} = \frac{c \cdot N_{rFFT}}{2B}Rmax=ΔR⋅NrFFT=2Bc⋅NrFFT
速度分辨率与观测时间成反比:
ΔV=λ2NdFFT⋅Tc=c2f0⋅NdFFT⋅Tc\Delta V = \frac{\lambda}{2N_{dFFT} \cdot T_c} = \frac{c}{2f_0 \cdot N_{dFFT} \cdot T_c}ΔV=2NdFFT⋅Tcλ=2f0⋅NdFFT⋅Tcc
最大无模糊速度为:
Vmax=NdFFT2⋅ΔV=λ4Tc=c4f0⋅TcV_{max} = \frac{N_{dFFT}}{2} \cdot \Delta V = \frac{\lambda}{4T_c} = \frac{c}{4f_0 \cdot T_c}Vmax=2NdFFT⋅ΔV=4Tcλ=4f0⋅Tcc
从这些公式可以看出一个重要的设计矛盾:提高速度分辨率需要增加TcT_cTc(延长观测时间),但这会同时降低最大无模糊速度。例如,当f0=76.5f_0 = 76.5f0=76.5 GHz,Tc=40T_c = 40Tc=40 μs时,Vmax=c/(4×76.5×109×40×10−6)=24.5V_{max} = c/(4 \times 76.5 \times 10^9 \times 40 \times 10^{-6}) = 24.5Vmax=c/(4×76.5×109×40×10−6)=24.5 m/s(约88 km/h),这对于高速公路场景是不够的。
3. 多模式复合波形设计
3.1 波形模式划分策略
现代汽车雷达系统通常需要在不同的距离范围内工作,每个范围有其特定的性能需求。本研究将雷达工作范围划分为三个模式:
- 短程雷达(SRR) :工作范围0-60米,主要用于泊车辅助、低速防碰撞等场景,需要极高的距离分辨率
- 中程雷达(MRR) :工作范围60-100米,用于变道辅助、盲点检测等,需要平衡距离和速度分辨率
- 远程雷达(LRR) :工作范围100-200米,用于自适应巡航、高速防碰撞等,需要更远的探测距离
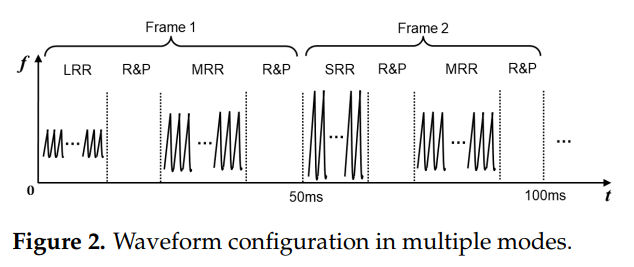
图2描述:多模式波形配置时序图展示了两个连续帧的波形安排。每帧持续50毫秒,第一帧包含LRR和MRR模式的波形,第二帧包含SRR和MRR模式的波形。每种模式后都有专门的接收和处理(R&P)时间窗口。通过这种交替配置,系统能在100毫秒(两帧)内完成所有三种模式的探测。
3.2 波形参数设计流程
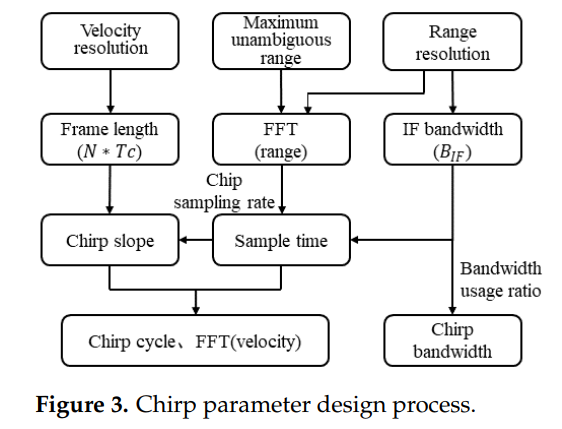
图3描述 :波形参数设计流程图展示了从系统需求到具体参数的推导过程。流程开始于速度分辨率(ΔV\Delta VΔV)和距离分辨率(ΔR\Delta RΔR)的需求定义,然后计算帧长度(N×TcN \times T_cN×Tc)和FFT图像,接着确定距离FFT点数(NrFFTN_{rFFT}NrFFT)和中频带宽,基于采样率计算调频斜率,最终确定调频周期、采样时间和带宽利用率。
设计流程的数学推导如下:
首先,根据期望的速度分辨率确定观测时间:
Tobs=NdFFT⋅Tc=λ2ΔVT_{obs} = N_{dFFT} \cdot T_c = \frac{\lambda}{2\Delta V}Tobs=NdFFT⋅Tc=2ΔVλ
然后,根据最大探测距离确定距离FFT点数:
NrFFT=2B⋅RmaxcN_{rFFT} = \frac{2B \cdot R_{max}}{c}NrFFT=c2B⋅Rmax
采样时间由ADC采样率决定:
Ts=NrFFTFsT_s = \frac{N_{rFFT}}{F_s}Ts=FsNrFFT
其中FsF_sFs是ADC采样率。调频斜率通过带宽和有效扫频时间计算:
μ=BTu=BTc−Tidle\mu = \frac{B}{T_u} = \frac{B}{T_c - T_{idle}}μ=TuB=Tc−TidleB
其中TidleT_{idle}Tidle是调频间隔的空闲时间。
3.3 角雷达专用波形参数配置
基于角雷达的特殊需求,表1给出了4T4R系统的详细波形参数:
表1:4T4R角雷达波形参数
| 参数 | SRR | MRR | 泊车模式 |
|---|---|---|---|
| 中心频率 | 76.5 GHz | 76.5 GHz | 77 GHz |
| 频率带宽 | 860 MHz | 600 MHz | 2500 MHz |
| 调频周期 | 36 μs | 36 μs | 36 μs |
| 调频数量 | 512 | 512 | 256×2 |
| 总时长 | 18.432 ms | 18.432 ms | 18.432 ms |
| 上升/下降时间 | 30/4 μs | 30/3 μs | 14/2 μs |
| ADC采样率 | 20 MHz | 20 MHz | 40 MHz |
| 距离分辨率 | 0.204 m | 0.293 m | 0.0656 m |
| 速度分辨率 | 0.096 m/s | 0.096 m/s | 0.096 m/s |
| 最大无模糊速度 | ±24.5 m/s | ±24.5 m/s | ±24.5 m/s |
泊车模式采用了2.5 GHz的超大带宽,实现了6.56厘米的超高距离分辨率,这对于精确的泊车操作至关重要。
4. AB波速度解模糊算法
4.1 理论基础:中国剩余定理的应用
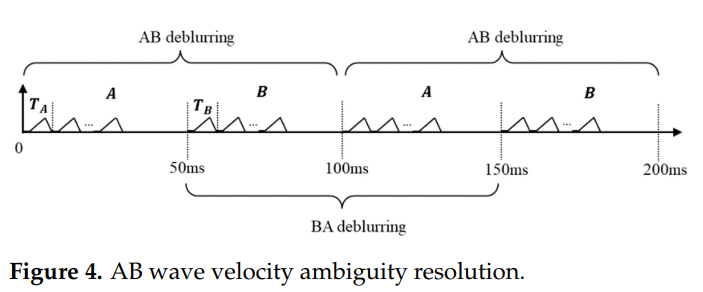
图4描述 :AB波速度解模糊原理图展示了两种不同重复周期的波形交替使用的时序。A波和B波具有不同的调频周期(TAT_ATA和TBT_BTB),在时间轴上交替出现。每50毫秒为一个机器周期,第一个50毫秒发送A波,第二个50毫秒发送B波,然后循环。图中标注了AB解模糊的工作窗口,显示了如何利用前后帧的信息进行速度解模糊。
基于中国剩余定理,当使用NNN组具有不同重复周期的波形时,设重复周期为{T1,T2,...,TN}\{T_1, T_2, ..., T_N\}{T1,T2,...,TN},对应的重复频率满足:
{F1:F2:...:FN}={K1:K2:...:KN}\{F_1 : F_2 : ... : F_N\} = \{K_1 : K_2 : ... : K_N\}{F1:F2:...:FN}={K1:K2:...:KN}
其中K1,K2,...,KNK_1, K_2, ..., K_NK1,K2,...,KN为互质的正整数。目标的真实多普勒频率在不同波形下表现为:
fD=fd1+k1⋅F1=fd2+k2⋅F2=...=fdN+kN⋅FNf_D = f_{d1} + k_1 \cdot F_1 = f_{d2} + k_2 \cdot F_2 = ... = f_{dN} + k_N \cdot F_NfD=fd1+k1⋅F1=fd2+k2⋅F2=...=fdN+kN⋅FN
理论上可解决的最大模糊倍数为∏i=1NKi\prod_{i=1}^{N} K_i∏i=1NKi。
4.2 目标匹配算法详细流程
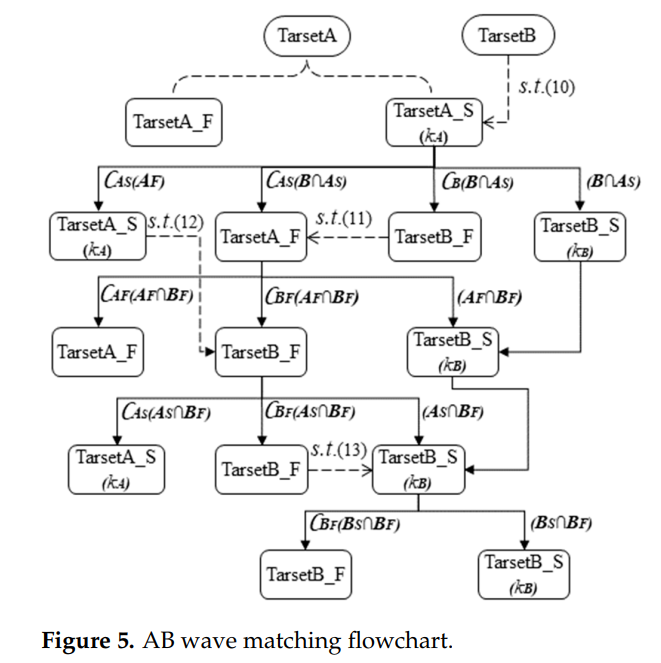
图5描述:AB波匹配流程图详细展示了速度解模糊的完整算法流程。流程从TarsetA和TarsetB两个目标集合开始,经过多级匹配过程。首先是基于A的主目标匹配,将TarsetA_S与TarsetB进行匹配;然后是基于A的次级匹配,处理TarsetA_F中未匹配的目标;接着是基于B的主目标匹配和次级匹配。每个匹配步骤都有相应的判断条件和输出结果,最终得到完全解模糊的TarsetB_S集合。
算法的核心匹配过程包括以下步骤:
步骤1:距离预测
对于前一帧(A波)中已解模糊的目标,其真实速度为:
VA′=VA+kA⋅VmaxAV'A = V_A + k_A \cdot V{maxA}VA′=VA+kA⋅VmaxA
预测该目标在B波中的距离:
RA′=RA+VA′⋅TAR'_A = R_A + V'_A \cdot T_ARA′=RA+VA′⋅TA
步骤2:主目标匹配
对于B波中的每个潜在模糊倍数kik_iki,计算对应的速度:
VBi′=VB+ki⋅VmaxB,i∈[−m,m]V'{Bi} = V_B + k_i \cdot V{maxB}, \quad i \in [-m, m]VBi′=VB+ki⋅VmaxB,i∈[−m,m]
定义匹配度量:
THR=∣RA′−RB∣THVi=∣VA′−VBi′∣THθ=∣θA−θB∣THS=∣SNRA−SNRB∣\begin{aligned} THR &= |R'A - R_B| \\ TH{Vi} &= |V'A - V'{Bi}| \\ TH_\theta &= |\theta_A - \theta_B| \\ TH_S &= |SNR_A - SNR_B| \end{aligned}THRTHViTHθTHS=∣RA′−RB∣=∣VA′−VBi′∣=∣θA−θB∣=∣SNRA−SNRB∣
通过最小化加权匹配误差确定正确的模糊倍数:
kB=argmini(a1⋅THR+a2⋅THVi+a3⋅THθ+a4⋅THS)k_B = \arg\min_i (a_1 \cdot THR + a_2 \cdot TH_{Vi} + a_3 \cdot TH_\theta + a_4 \cdot TH_S)kB=argimin(a1⋅THR+a2⋅THVi+a3⋅THθ+a4⋅THS)
其中a1,a2,a3,a4a_1, a_2, a_3, a_4a1,a2,a3,a4是权重系数,可根据参数估计的可靠性进行调整。
5. 仿真实验与结果分析
5.1 仿真场景设置
仿真实验设置了三个典型目标来验证算法性能:
- 目标T1:距离160米,速度0 m/s,方位角30°,模拟远距离静止目标
- 目标T2:距离105米,速度-30 m/s,方位角10°,模拟中距离接近目标
- 目标T3:距离60米,速度75 m/s,方位角-15°,模拟近距离高速目标
表2:仿真波形参数
| 参数 | LRR (A波) | LRR (B波) |
|---|---|---|
| 中心频率 | 76.5 GHz | 76.5 GHz |
| 频率带宽 | 430 MHz | 430 MHz |
| 上升周期 | 29 μs | 29 μs |
| 下降周期 | 4 μs | 5 μs |
| 调频周期 | 36 μs | 40 μs |
| 最大无模糊速度 | ±27.2 m/s | ±24.5 m/s |
| 速度分辨率 | 0.11 m/s | 0.096 m/s |
5.2 仿真结果展示
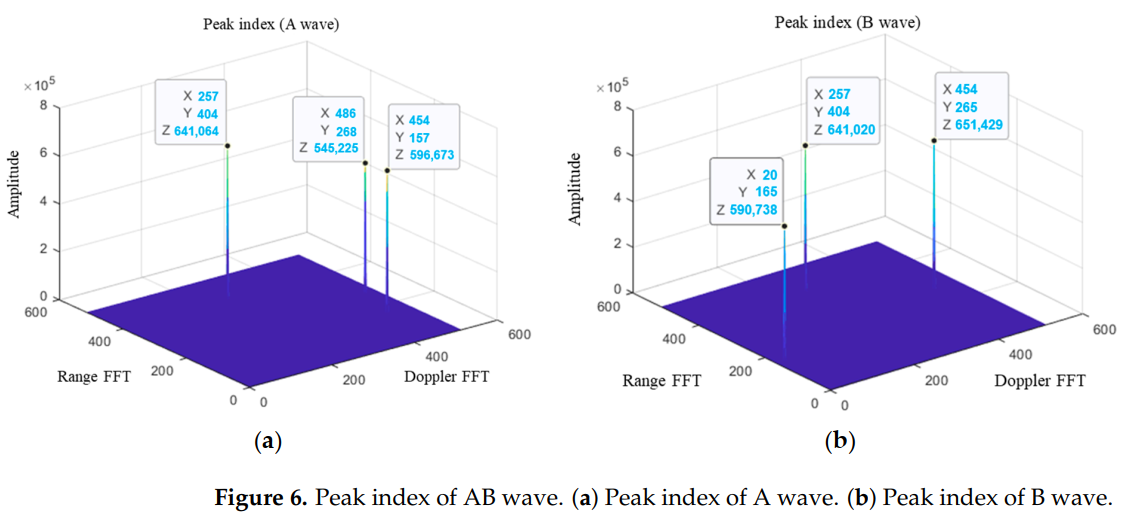
图6描述:AB波的峰值索引图展示了三个目标在距离-速度维度的位置。(a)图显示A波的检测结果,(b)图显示B波的检测结果。可以清楚地看到T1在两个波形中都没有速度模糊(位于中心附近),而T2和T3由于速度超出无模糊范围,在两个波形中显示出不同的速度值,这正是速度模糊的表现。
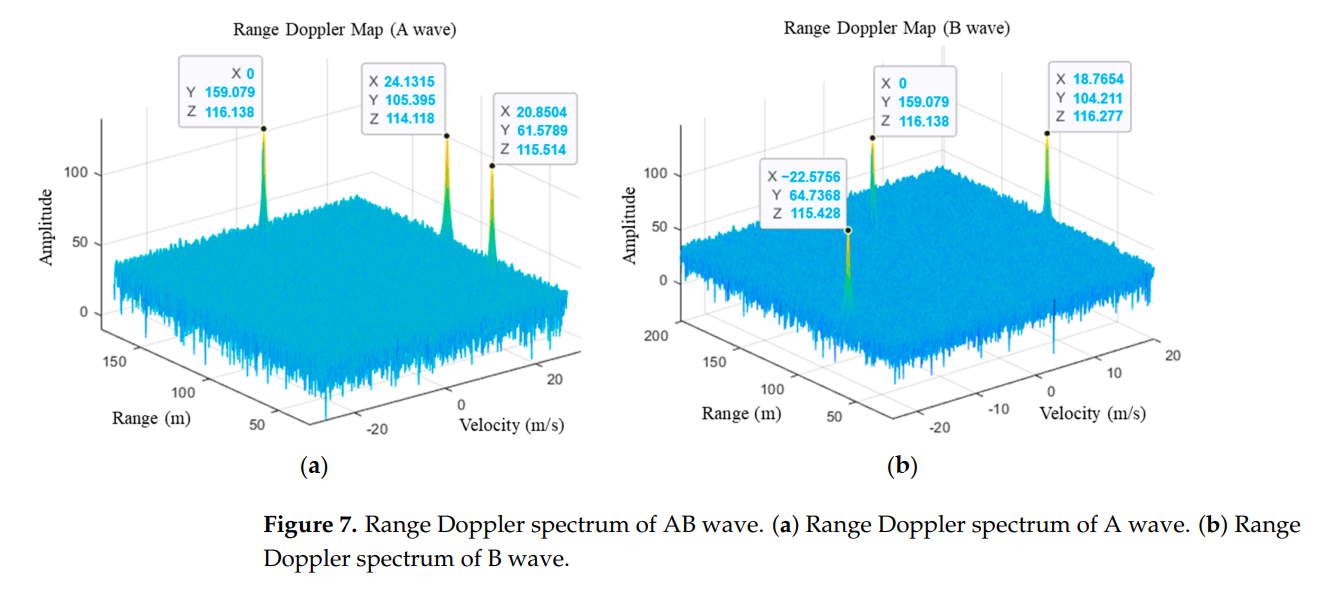
图7描述:距离-多普勒频谱图以三维形式展示了目标的能量分布。(a)图为A波的频谱,(b)图为B波的频谱。图中标注了每个目标的具体位置坐标。T1在(159.079m, 0m/s)位置,T2在A波中显示为(105.395m, -30.2685m/s),在B波中由于速度模糊显示为(104.211m, 18.7654m/s)。T3同样在两个波形中显示出不同的速度值。
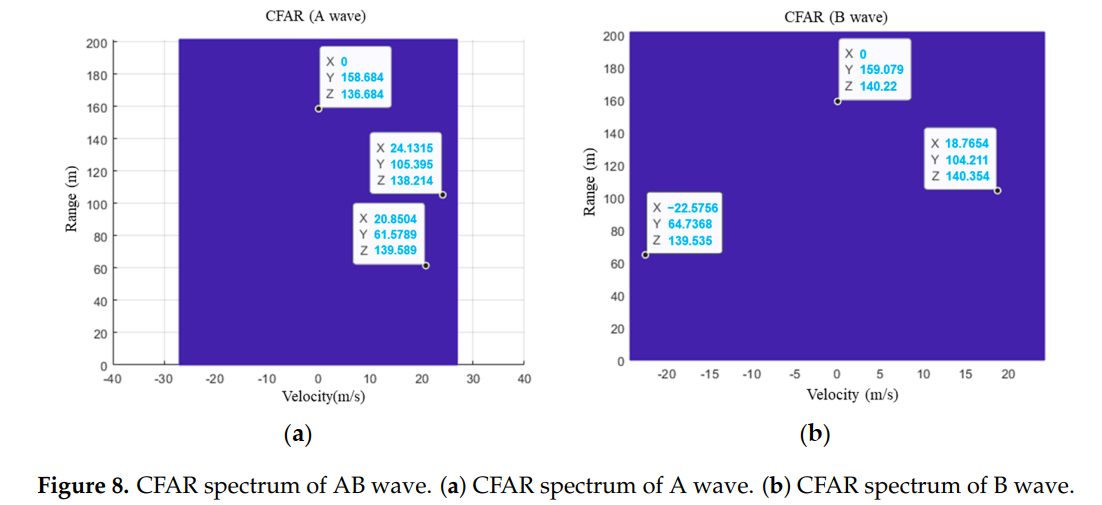
图8描述:CFAR检测结果图展示了恒虚警处理后的目标检测输出。(a)图和(b)图分别对应A波和B波的CFAR输出。每个检测到的目标都标注了其距离和速度信息。这些检测结果作为速度解模糊算法的输入。
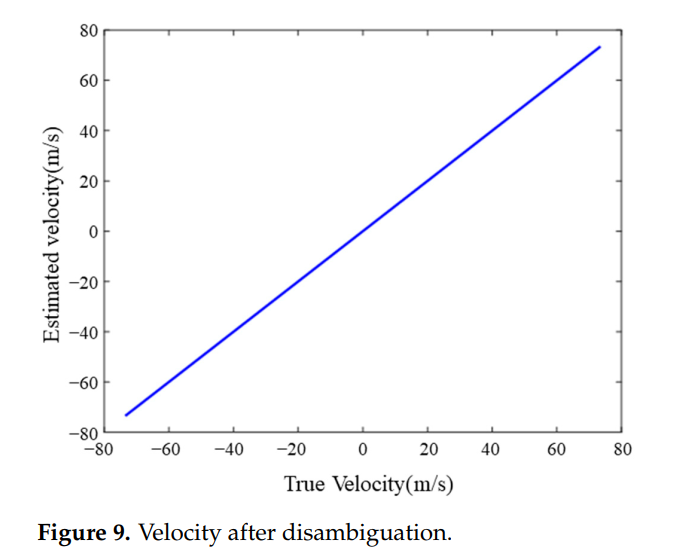
图9描述:速度解模糊后的结果图展示了算法成功恢复了目标的真实速度。横轴表示真实速度(-80到80 m/s),纵轴表示估计速度。图中的直线表示理想的估计结果,所有三个目标点都准确地落在这条直线上,证明了解模糊算法的有效性。
5.3 匹配过程分析
表4:AB波匹配仿真结果
| 目标参数 | T1 | T2 | T3 |
|---|---|---|---|
| RAR_ARA (m) | 159.079 | 105.395 | 61.5789 |
| VAV_AVA (m/s) | 0 | -30.2685 | 75.2504 |
| RA′R'_ARA′ (m) | 159.079 | 103.882 | 65.0916 |
| RBR_BRB (m) | 159.079 | 104.211 | 64.7368 |
| VBV_BVB (m/s) | 0 | 18.7654 | -22.5756 |
| kBk_BkB候选值 | 0/0/0 | -30.23/18.76/67.77 | -71.58/-22.58/26.58/75.58 |
| 匹配结果kBk_BkB | 0 | -1 | 2 |
通过表4可以看出,算法成功地为每个目标找到了正确的模糊倍数。T1由于速度为0,不存在模糊;T2的模糊倍数为-1,真实速度为18.7654+(−1)×49=−30.234618.7654 + (-1) \times 49 = -30.234618.7654+(−1)×49=−30.2346 m/s;T3的模糊倍数为2,真实速度为−22.5756+2×49=75.4244-22.5756 + 2 \times 49 = 75.4244−22.5756+2×49=75.4244 m/s。
6. 实验验证
6.1 实验设置
实验使用了基于Alps Pro芯片的雷达系统。Alps Pro是加特兰于2022年底推出的雷达芯片,支持DDMA传输模式,最大支持4T4R配置。实验在南京的一条半封闭道路上进行,角雷达安装在主车左后方45°位置。

图10描述:(a)图展示了测试场景,一条笔直的半封闭道路,两侧有树木,确保了测试的安全性。(b)图展示了测试用的雷达设备,包括Alps Pro雷达板和连接的数据采集系统。雷达未加装外壳,直接暴露PCB板和天线阵列。
为了适应实际测试条件,将TcT_cTc调整为42 μs,使最大无模糊速度降至23.3 m/s,这样可以在安全的车速下验证速度模糊现象。
6.2 速度解模糊验证结果
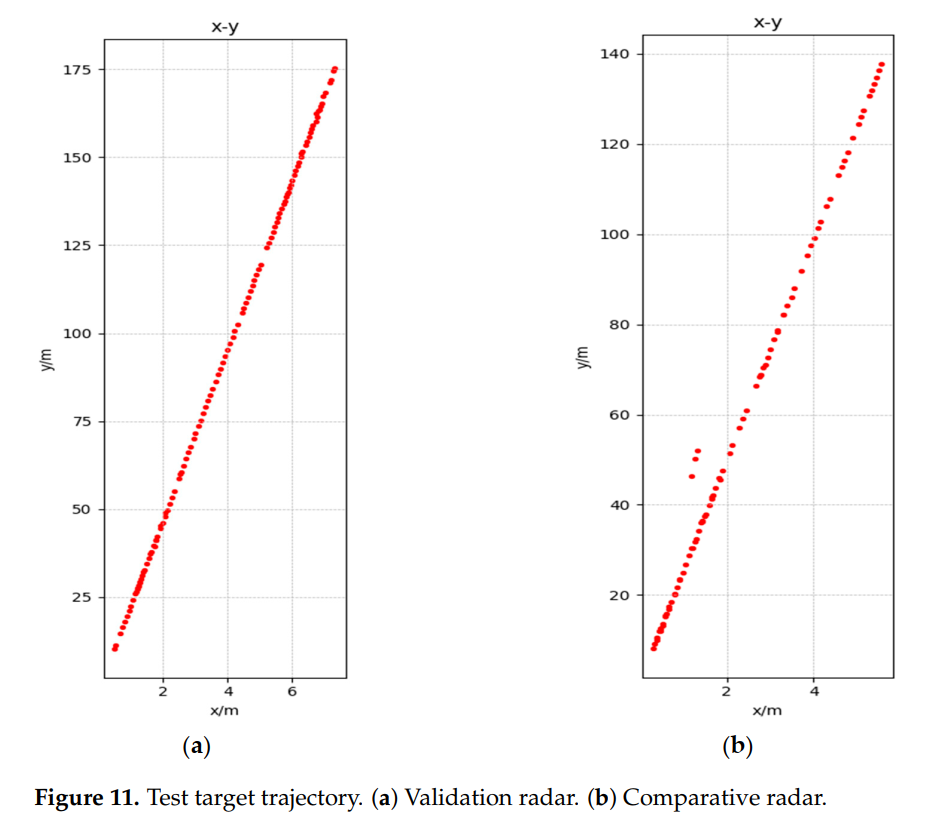
图11描述:目标运动轨迹图展示了目标车辆在雷达坐标系中的完整运动路径。(a)图为验证雷达的检测结果,(b)图为对比雷达的结果。红色点表示目标从175米处接近到约10米处的完整轨迹。两个雷达的轨迹高度一致,验证了系统的可靠性。
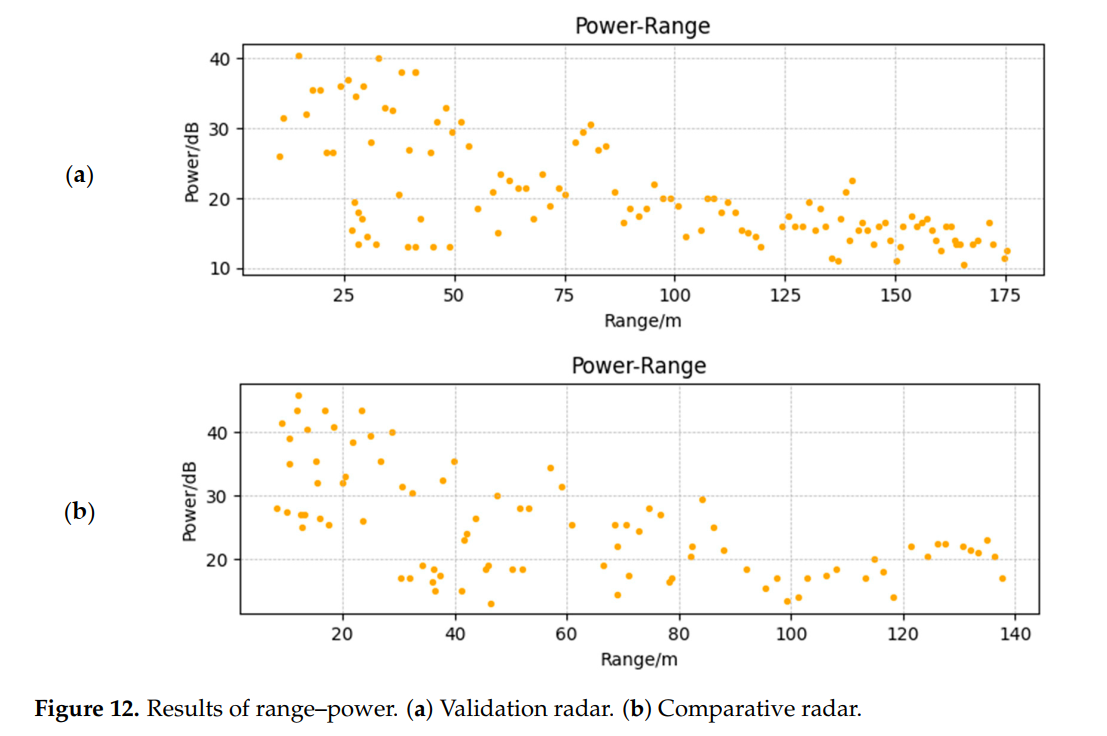
图12描述:距离-功率关系图显示了目标在不同距离上的回波功率。(a)图和(b)图分别对应验证雷达和对比雷达。可以看到功率随距离增加而衰减的趋势,符合雷达方程的理论预期。两个雷达的功率曲线基本一致。
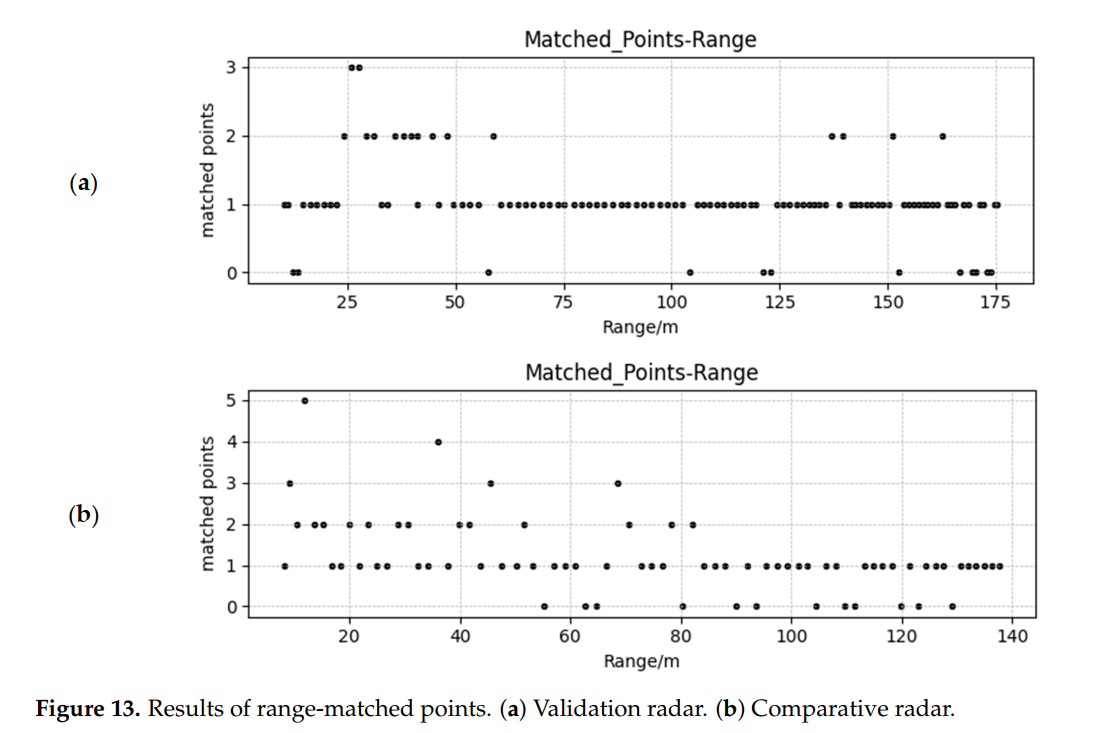
图13描述:距离-匹配点数关系图展示了在不同距离上检测到的目标点数量。近距离时由于信号强度高,可以检测到多个散射点(最多3-4个),随着距离增加逐渐减少到1个点。这种变化规律符合预期。
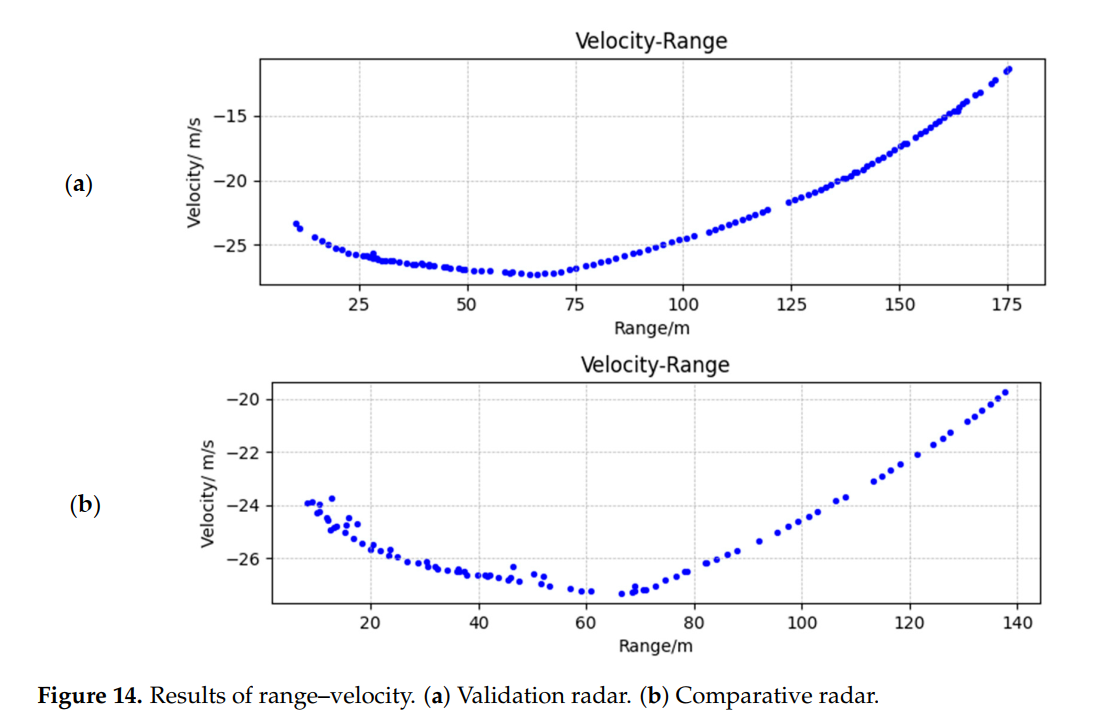
图14描述:距离-速度关系图是验证速度解模糊的关键结果。(a)图显示验证雷达在67米处检测到最大速度27.4 m/s(超过了23.3 m/s的无模糊范围),但通过解模糊算法正确恢复了真实速度。(b)图的对比雷达显示最大速度为27.5 m/s,两者高度吻合,误差仅0.1 m/s。
6.3 多模式波形性能对比
为了验证多模式波形的优势,进行了对比实验,在相同条件下比较多模式波形和单一LRR模式波形的性能。
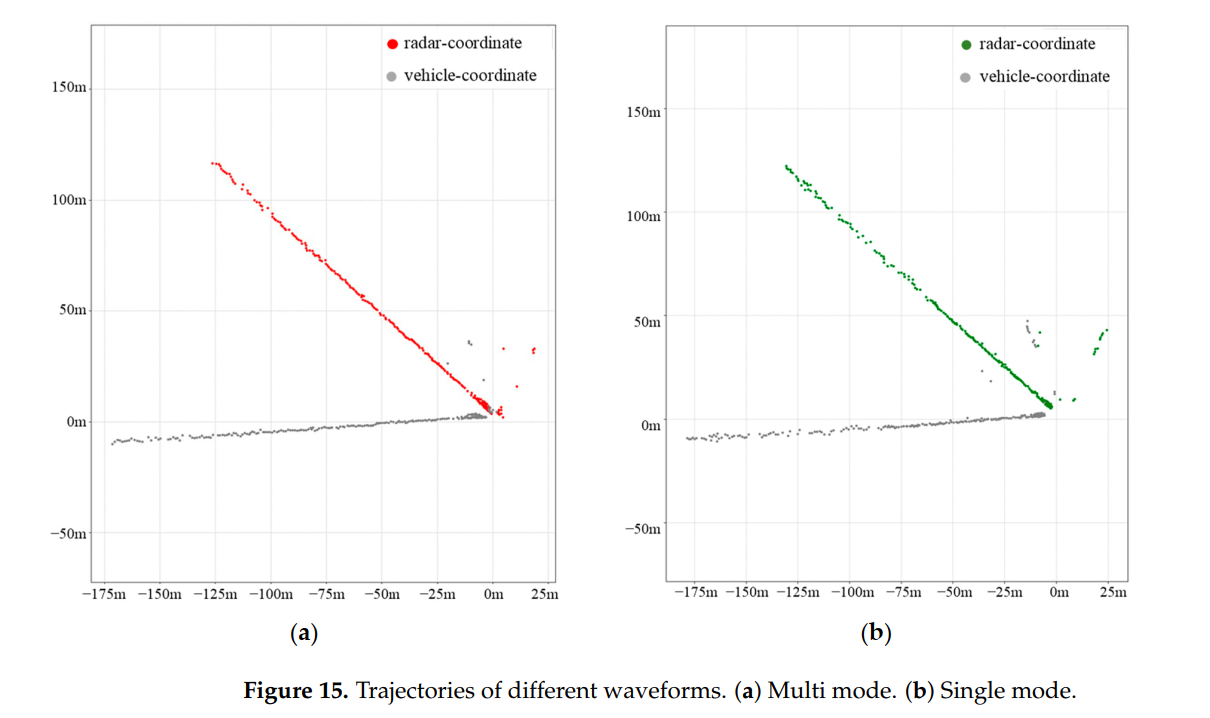
图15描述:不同波形的目标轨迹对比图。(a)图显示多模式波形的检测结果,(b)图显示单模式波形的结果。红色和绿色线分别表示雷达坐标系中的轨迹,灰色线表示车辆坐标系轨迹。在60-100米范围内,多模式波形的目标点明显更密集。
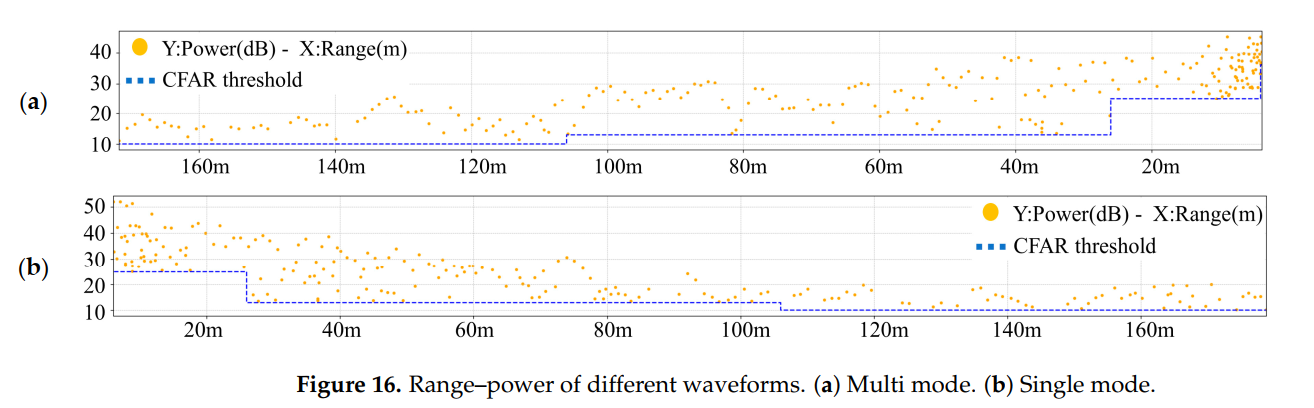
图16描述:不同波形的距离-功率对比。两种波形使用相同的CFAR门限,在各个距离上的检测功率基本一致,说明多模式波形没有牺牲检测灵敏度。
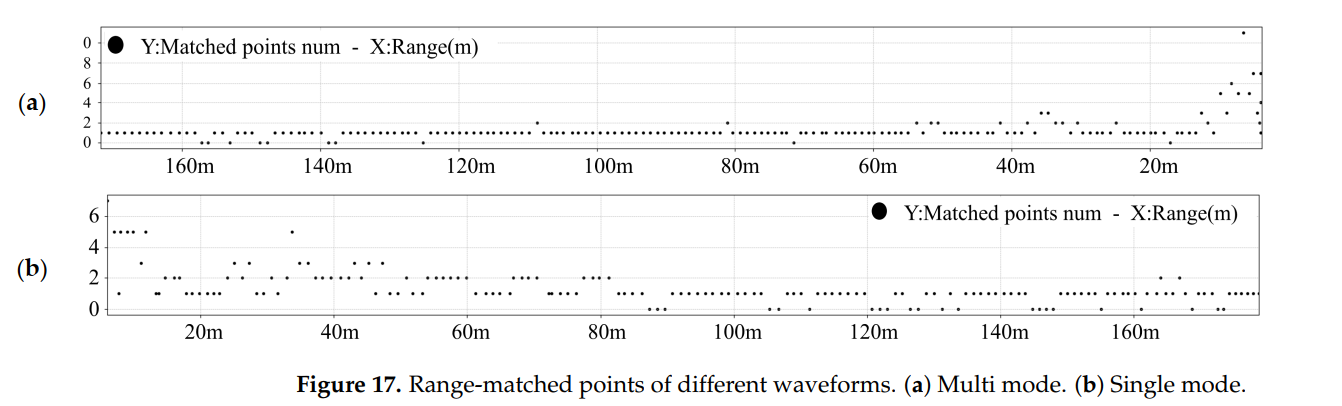
图17描述:距离-匹配点数对比清楚地展示了多模式波形的优势。在80-140米范围内,多模式波形由于更高的分辨率,漏检点更少,检测的连续性更好。
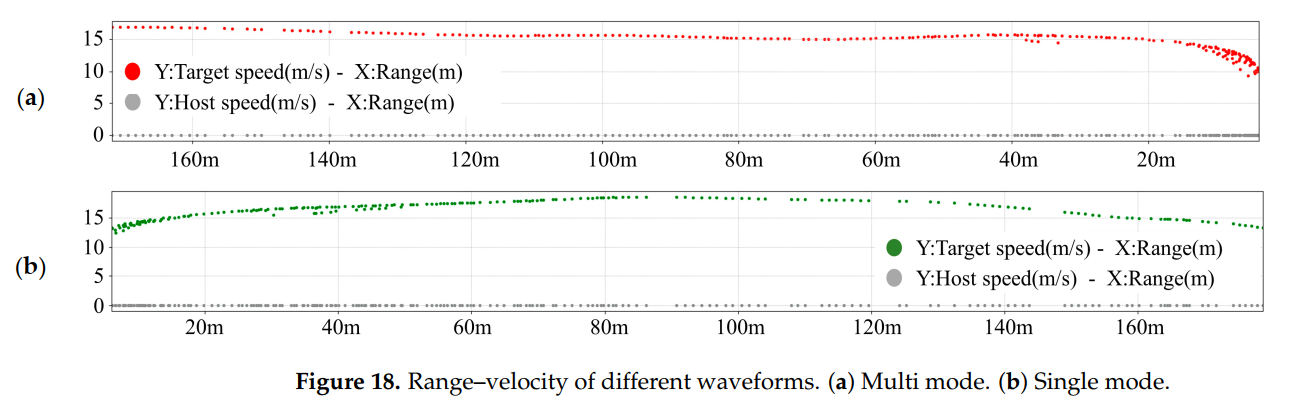
图18描述:距离-速度关系对比。两个雷达由于安装位置不同(左后和右后),检测到的径向速度略有差异,这是由道路曲率和目标运动方向造成的正常现象。
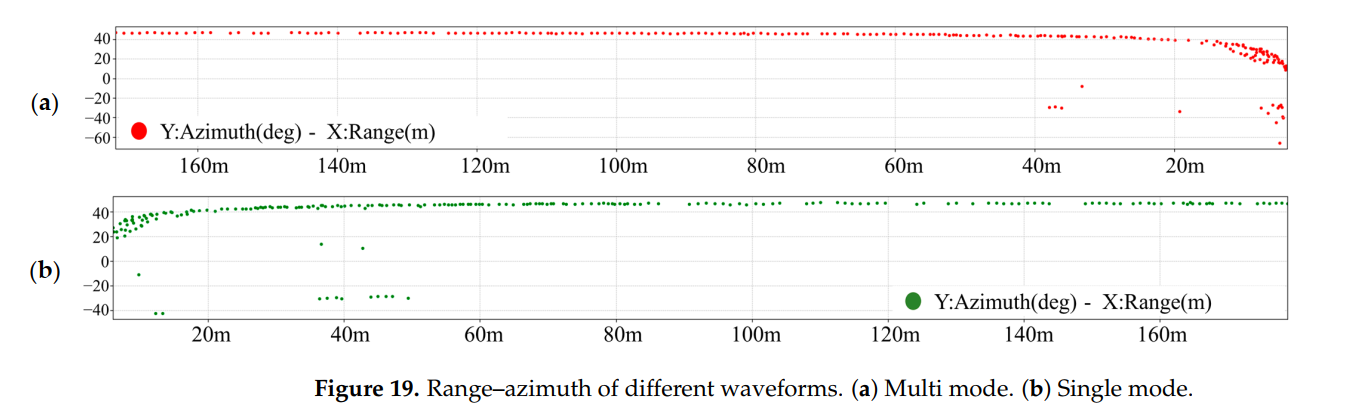
图19描述:距离-方位角关系对比。尽管速度测量有差异,但两个雷达的角度测量结果基本一致,验证了系统的角度测量精度。
7. 结论
本研究成功开发了一种针对汽车角雷达的FMCW MIMO单帧多模式波形设计方案及其配套的速度解模糊算法。主要创新点和贡献包括:
-
多模式波形设计:提出了SRR、MRR、LRR三种模式的统一框架,通过在单帧内配置不同参数的波形,实现了探测距离和分辨率的最优平衡。特别是为泊车场景设计的2.5 GHz带宽波形,实现了6.56厘米的超高距离分辨率。
-
AB波速度解模糊算法:基于中国剩余定理和目标参数匹配,开发了一种鲁棒的速度解模糊方法。该方法不仅适用于当前的TDMA系统,还能无缝迁移到未来的DDMA传输模式。
-
实验验证:通过仿真和实车测试全面验证了所提方案的有效性。实验结果表明,该方法能够准确恢复超出无模糊范围的目标速度,误差控制在0.1 m/s以内。
-
工程可行性:基于商用Alps Pro芯片的成功实现证明了该方案的工程可行性,为当前汽车雷达系统的设计提供了实用的参考方案。
附录A:速度模糊的数学推导
A.1 多普勒效应与频率关系
考虑一个以径向速度vrv_rvr运动的点目标,雷达发射信号为:
st(t)=Atexp[j2π(f0t+μt22)]s_t(t) = A_t \exp\left[j2\pi\left(f_0t + \frac{\mu t^2}{2}\right)\right]st(t)=Atexp[j2π(f0t+2μt2)]
其中AtA_tAt是发射信号幅度,f0f_0f0是载波频率,μ\muμ是调频斜率。
目标距离随时间变化:
R(t)=R0+vrtR(t) = R_0 + v_r tR(t)=R0+vrt
其中R0R_0R0是初始距离。信号往返时延:
τ(t)=2R(t)c=2(R0+vrt)c=τ0+2vrtc\tau(t) = \frac{2R(t)}{c} = \frac{2(R_0 + v_r t)}{c} = \tau_0 + \frac{2v_r t}{c}τ(t)=c2R(t)=c2(R0+vrt)=τ0+c2vrt
接收信号为:
sr(t)=Arexp[j2π(f0(t−τ(t))+μ(t−τ(t))22)]s_r(t) = A_r \exp\left[j2\pi\left(f_0(t-\tau(t)) + \frac{\mu(t-\tau(t))^2}{2}\right)\right]sr(t)=Arexp[j2π(f0(t−τ(t))+2μ(t−τ(t))2)]
A.2 中频信号推导
混频后的基带信号:
sIF(t)=st(t)⋅sr∗(t)s_{IF}(t) = s_t(t) \cdot s_r^*(t)sIF(t)=st(t)⋅sr∗(t)
展开并忽略高阶小项(假设τ(t)≪t\tau(t) \ll tτ(t)≪t):
sIF(t)≈AIFexp[j2π(μτ0t+f0τ0−2vrf0ct)]s_{IF}(t) \approx A_{IF} \exp\left[j2\pi\left(\mu\tau_0 t + f_0\tau_0 - \frac{2v_rf_0}{c}t\right)\right]sIF(t)≈AIFexp[j2π(μτ0t+f0τ0−c2vrf0t)]
瞬时频率为:
fIF(t)=12πdϕ(t)dt=μτ0−2vrf0c=fb−fdf_{IF}(t) = \frac{1}{2\pi}\frac{d\phi(t)}{dt} = \mu\tau_0 - \frac{2v_rf_0}{c} = f_b - f_dfIF(t)=2π1dtdϕ(t)=μτ0−c2vrf0=fb−fd
其中fb=μτ0=2μR0/cf_b = \mu\tau_0 = 2\mu R_0/cfb=μτ0=2μR0/c是拍频,fd=2vrf0/cf_d = 2v_rf_0/cfd=2vrf0/c是多普勒频率。
A.3 离散采样与频谱分析
对NNN个调频周期进行采样,每个周期采样MMM个点。二维FFT后,在距离-多普勒域得到:
S(m,n)=∑k=0N−1∑l=0M−1sIF(kTc+lTs)exp[−j2π(mlM+knN)]S(m,n) = \sum_{k=0}^{N-1}\sum_{l=0}^{M-1} s_{IF}(kT_c + lT_s) \exp\left[-j2\pi\left(\frac{ml}{M} + \frac{kn}{N}\right)\right]S(m,n)=k=0∑N−1l=0∑M−1sIF(kTc+lTs)exp[−j2π(Mml+Nkn)]
其中mmm是距离单元索引,nnn是速度单元索引。
距离分辨单元:
δR=c2Beff=c2μTsM\delta R = \frac{c}{2B_{eff}} = \frac{c}{2\mu T_s M}δR=2Beffc=2μTsMc
速度分辨单元:
δV=λ2NTc\delta V = \frac{\lambda}{2NT_c}δV=2NTcλ
A.4 模糊数学分析
当真实多普勒频率fdtruef_d^{true}fdtrue超出[−PRF/2,PRF/2][-PRF/2, PRF/2][−PRF/2,PRF/2]范围时,观测到的频率为:
fdobs=fdtrue−k⋅PRFf_d^{obs} = f_d^{true} - k \cdot PRFfdobs=fdtrue−k⋅PRF
其中k=⌊(fdtrue+PRF/2)/PRF⌋k = \lfloor (f_d^{true} + PRF/2)/PRF \rfloork=⌊(fdtrue+PRF/2)/PRF⌋。
对应的速度关系:
vobs=vtrue−k⋅vmaxv^{obs} = v^{true} - k \cdot v_{max}vobs=vtrue−k⋅vmax
其中vmax=λ⋅PRF/4v_{max} = \lambda \cdot PRF/4vmax=λ⋅PRF/4。
附录B:中国剩余定理在雷达中的应用
B.1 定理陈述
设m1,m2,...,mnm_1, m_2, ..., m_nm1,m2,...,mn是两两互质的正整数,M=∏i=1nmiM = \prod_{i=1}^n m_iM=∏i=1nmi。对于任意整数a1,a2,...,ana_1, a_2, ..., a_na1,a2,...,an,同余方程组:
{x≡a1(modm1)x≡a2(modm2)⋮x≡an(modmn)\begin{cases} x \equiv a_1 \pmod{m_1} \\ x \equiv a_2 \pmod{m_2} \\ \vdots \\ x \equiv a_n \pmod{m_n} \end{cases}⎩ ⎨ ⎧x≡a1(modm1)x≡a2(modm2)⋮x≡an(modmn)
有唯一解:
x=∑i=1naiMiMi−1(modM)x = \sum_{i=1}^n a_i M_i M_i^{-1} \pmod{M}x=i=1∑naiMiMi−1(modM)
其中Mi=M/miM_i = M/m_iMi=M/mi,Mi−1M_i^{-1}Mi−1是MiM_iMi模mim_imi的逆元。
B.2 在速度解模糊中的应用
对于两个不同PRF的波形(PRF₁和PRF₂),设其比值为互质整数:
PRF1PRF2=K1K2,gcd(K1,K2)=1\frac{PRF_1}{PRF_2} = \frac{K_1}{K_2}, \quad \gcd(K_1, K_2) = 1PRF2PRF1=K2K1,gcd(K1,K2)=1
真实速度vvv在两个波形中的观测值:
{v1obs=v−k1⋅vmax1v2obs=v−k2⋅vmax2\begin{cases} v_1^{obs} = v - k_1 \cdot v_{max1} \\ v_2^{obs} = v - k_2 \cdot v_{max2} \end{cases}{v1obs=v−k1⋅vmax1v2obs=v−k2⋅vmax2
由于vmax∝PRFv_{max} \propto PRFvmax∝PRF,有:
vmax1vmax2=PRF1PRF2=K1K2\frac{v_{max1}}{v_{max2}} = \frac{PRF_1}{PRF_2} = \frac{K_1}{K_2}vmax2vmax1=PRF2PRF1=K2K1
设vmax2=v0K2v_{max2} = v_0 K_2vmax2=v0K2,vmax1=v0K1v_{max1} = v_0 K_1vmax1=v0K1,则:
{v=v1obs+k1⋅v0K1v=v2obs+k2⋅v0K2\begin{cases} v = v_1^{obs} + k_1 \cdot v_0 K_1 \\ v = v_2^{obs} + k_2 \cdot v_0 K_2 \end{cases}{v=v1obs+k1⋅v0K1v=v2obs+k2⋅v0K2
消去vvv得到:
v1obs−v2obs=k2⋅v0K2−k1⋅v0K1v_1^{obs} - v_2^{obs} = k_2 \cdot v_0 K_2 - k_1 \cdot v_0 K_1v1obs−v2obs=k2⋅v0K2−k1⋅v0K1
即:
v1obs−v2obsv0=k2K2−k1K1\frac{v_1^{obs} - v_2^{obs}}{v_0} = k_2 K_2 - k_1 K_1v0v1obs−v2obs=k2K2−k1K1
这个方程在模K1K2K_1 K_2K1K2意义下有唯一解,最大可解模糊倍数为K1×K2K_1 \times K_2K1×K2。
B.3 实际实现考虑
在实际系统中,由于测量噪声的存在,需要在整数域附近搜索:
k^=argmink1,k2∣v1obs+k1vmax1−(v2obs+k2vmax2)∣\hat{k} = \arg\min_{k_1,k_2} |v_1^{obs} + k_1 v_{max1} - (v_2^{obs} + k_2 v_{max2})|k^=argk1,k2min∣v1obs+k1vmax1−(v2obs+k2vmax2)∣
搜索范围通常限制在∣ki∣≤⌈vexpectedmax/vmaxi⌉|k_i| \leq \lceil v_{expected}^{max}/v_{maxi} \rceil∣ki∣≤⌈vexpectedmax/vmaxi⌉。
附录C:目标参数匹配的最优化理论
C.1 匹配代价函数
定义目标在相邻帧间的匹配代价函数:
J(k)=∑i=14αi⋅di(k)J(k) = \sum_{i=1}^4 \alpha_i \cdot d_i(k)J(k)=i=1∑4αi⋅di(k)
其中:
- d1(k)=∣RB−(RA+vA(k)⋅Δt)∣d_1(k) = |R_B - (R_A + v_A^{(k)} \cdot \Delta t)|d1(k)=∣RB−(RA+vA(k)⋅Δt)∣ - 距离预测误差
- d2(k)=∣vB(k)−vA(k)∣d_2(k) = |v_B^{(k)} - v_A^{(k)}|d2(k)=∣vB(k)−vA(k)∣ - 速度一致性误差
- d3(k)=∣θB−θA∣d_3(k) = |\theta_B - \theta_A|d3(k)=∣θB−θA∣ - 角度偏差
- d4(k)=∣SNRB−SNRA∣d_4(k) = |SNR_B - SNR_A|d4(k)=∣SNRB−SNRA∣ - 信噪比差异
C.2 权重优化
权重系数αi\alpha_iαi可通过最大似然估计获得。假设各参数估计误差服从高斯分布:
p(di)=12πσi2exp(−di22σi2)p(d_i) = \frac{1}{\sqrt{2\pi\sigma_i^2}} \exp\left(-\frac{d_i^2}{2\sigma_i^2}\right)p(di)=2πσi2 1exp(−2σi2di2)
最大似然估计等价于最小化:
JML(k)=∑i=14di2(k)2σi2J_{ML}(k) = \sum_{i=1}^4 \frac{d_i^2(k)}{2\sigma_i^2}JML(k)=i=1∑42σi2di2(k)
因此最优权重为:
αi=12σi2\alpha_i = \frac{1}{2\sigma_i^2}αi=2σi21
C.3 门限自适应
匹配门限应根据信噪比自适应调整:
Thi=βi⋅σi⋅1+1SNRTh_i = \beta_i \cdot \sigma_i \cdot \sqrt{1 + \frac{1}{SNR}}Thi=βi⋅σi⋅1+SNR1
其中βi\beta_iβi是置信度系数(典型值为3对应99.7%置信区间)。
附录D:MIMO虚拟阵列与角度估计
D.1 虚拟阵列原理
对于MMM个发射天线和NNN个接收天线的MIMO系统,虚拟阵列包含M×NM \times NM×N个虚拟阵元。虚拟阵元位置为:
p⃗virtual=p⃗tx+p⃗rx\vec{p}{virtual} = \vec{p}{tx} + \vec{p}_{rx}p virtual=p tx+p rx
D.2 角度估计
使用FFT波束形成,目标角度估计为:
θ=arcsin(λ⋅kpeakNFFT⋅d)\theta = \arcsin\left(\frac{\lambda \cdot k_{peak}}{N_{FFT} \cdot d}\right)θ=arcsin(NFFT⋅dλ⋅kpeak)
其中kpeakk_{peak}kpeak是角度FFT峰值位置,ddd是天线间距。
角度分辨率:
Δθ=λNvirtual⋅d⋅cosθ\Delta\theta = \frac{\lambda}{N_{virtual} \cdot d \cdot \cos\theta}Δθ=Nvirtual⋅d⋅cosθλ
D.3 角度模糊
当d>λ/2d > \lambda/2d>λ/2时会产生栅瓣,导致角度模糊。无模糊角度范围:
θ∈[−arcsin(λ2d),arcsin(λ2d)]\theta \in \left[-\arcsin\left(\frac{\lambda}{2d}\right), \arcsin\left(\frac{\lambda}{2d}\right)\right]θ∈[−arcsin(2dλ),arcsin(2dλ)]
对于77 GHz雷达,λ≈3.9\lambda \approx 3.9λ≈3.9 mm,典型天线间距d=λ/2≈1.95d = \lambda/2 \approx 1.95d=λ/2≈1.95 mm可避免角度模糊。