CCF编程能力等级认证GESP---C++7级---20250927
- [单选题(每题 2 分,共 30 分)](#单选题(每题 2 分,共 30 分))
- [判断题(每题 2 分,共 20 分)](#判断题(每题 2 分,共 20 分))
- 编程题 (每题 25 分,共 50 分)
单选题(每题 2 分,共 30 分)
1、已知小写字母 b 的ASCII码为98,下列C++代码的输出结果是( )。
cpp
#include <iostream>
using namespace std;
int main() {
char a = 'b' + 1;
cout << a;
return 0;
}
cpp
A. b
B. c
C. 98
D. 99正确答案:B
2、已知 a 为 int 类型变量, p 为 int * 类型变量,下列表达式不符合语法的是( )。
cpp
A. a * a
B. p * p
C. a && a
D. p && p正确答案:B
3、 下列关于C++类的说法,错误的是( )。
cpp
A. 如果一个类包含纯虚函数,则它不能包含成员变量。
B. 如果一个类包含纯虚函数,则不能用它定义对象。
C. 派生类对象占用的内存总是不小于基类对象。
D. 派生类可以不实现基类的虚函数。正确答案:A
4、已知数组 a 的定义 int a[10] = {-1}; ,下列说法不正确的是( )。
cpp
A. 数组 a 至少占用 10 个 int 大小的内存,一般为 40 个字节。
B. 数组 a 的所有元素均被初始化为 -1 。
C. 语句 a[-1] = 0; 不会产生编译错误,但会导致难以预测的运行结果。
D. 语句 a[13] = 0; 不会产生编译错误,但会导致难以预测的运行结果。正确答案:B
5、一棵完全二叉树有165个结点,则叶结点有多少个?( )
cpp
A. 38
B. 82
C. 83
D. 84正确答案:C
6、下列关于二叉树的说法,错误的是( )。
A. 二叉排序树的中序遍历顺序与元素排序的顺序是相同的。
B. 自平衡二叉查找树(AVL树)是一种二叉排序树。
C. n个元素的二叉排序树,其高一定为 ⌊ l o g 2 n ⌋ \lfloor log_2n \rfloor ⌊log2n⌋ 。
D. 任意的森林,都可以映射为一颗二叉树进行表达和存储。
正确答案:C
7、下列关于树和图的说法,错误的是( )。
cpp
A. 保留树的所有节点,并把树的每个节点指向其父节点,则可以将树转换为一个有向弱连通图。
B. 保留树的所有节点,并把树的每个节点指向其子节点,则可以将树转换为一个有向无环图。
C. 每个连通图都存在生成树。
D. 每个存在生成树的有向图,都一定是强连通的。正确答案:D
8、对一个包含V个顶点、E条边的图,执行广度优先搜索,其最优时间复杂度是( )。
A. O ( V + E ) O(V+E) O(V+E)
B. O ( V ) O(V) O(V)
C. O ( E ) O(E) O(E)
D. O ( V 2 ) O(V^2) O(V2)
正确答案:A
9、 以下哪个方案不能合理解决或缓解哈希表冲突( )。
cpp
A. 用新元素覆盖发生冲突的哈希表项。
B. 在每个哈希表项处,使用单链表管理该表项的冲突元素。
C. 建立额外的单链表,用来管理所有发生冲突的元素。
D. 使用不同的哈希函数再建立一个哈希表,用来管理所有发生冲突的元素。正确答案:A
10、以下关于贪心法和动态规划的说法中,错误的是( )。
cpp
A. 对特定的问题,贪心法不一定适用。
B. 当特定的问题适用贪心法时,通常比动态规划的时间复杂度更低。
C. 对很多问题,递推实现和递归实现动态规划方法的时间复杂度相当。
D. 采用动态规划的算法一定具有多项式时间复杂度。正确答案:D
11、下面程序的输出为( )。
cpp
#include <iostream>
using namespace std;
int fib(int n) {
if (n == 0)
return 1;
return fib(n - 1) + fib(n - 2);
}
int main() {
cout << fib(6) << endl;
return 0;
}
cpp
A. 8
B. 13
C. 21
D. 无法正常结束。正确答案:D
12、下面程序的时间复杂度为( )。
cpp
int rec_fib[MAX_N];
int fib(int n) {
if (n <= 1)
return n;
if (rec_fib[n] != 0)
return rec_fib[n];
return fib(n - 1) + fib(n - 2);
}A. O ( φ n ) , φ = 5 + 1 2 O(\varphi^n), \varphi = \frac{\sqrt{5} + 1}{2} O(φn),φ=25 +1
B. O ( 2 n ) O(2^n) O(2n)
C. O ( n 2 ) O(n^2) O(n2)
D. O ( n ) O(n) O(n)
正确答案:A
13、下面 init_sieve 函数的时间复杂度为( )。
cpp
int sieve[MAX_N];
void init_sieve(int n) {
for (int i = 1; i <= n; i++)
sieve[i] = i;
for (int i = 2; i <= n; i++)
for (int j = i; j <= n; j += i)
sieve[j]--;
}A. O ( n ) O(n) O(n)
B. O ( n l o g l o g n ) O(n log logn) O(nloglogn)
C. O ( n l o g n ) O(nlogn) O(nlogn)
D. O ( n 2 ) O(n^2) O(n2)
正确答案:C
14、下面 count_triple 函数的时间复杂度为( )。
cpp
int gcd(int m, int n) {
if (m == 0) return n;
return gcd(n % m, m);
}
int count_triple(int n) {
int cnt = 0;
for (int v = 1; v * v * 4 <= n; v++)
for (int u = v + 1; u * (u + v) * 2 <= n; u += 2)
if (gcd(u, v) == 1) {
int a = u * u - v * v;
int b = u * v * 2;
int c = u * u + v * v;
cnt += n / (a + b + c);
}
return cnt;
}A. O ( n 2 ) O(n^2) O(n2)
B. O ( n 2 l o g n ) O(n^2 log n) O(n2logn)
C. O ( n l o g n ) O(nlogn) O(nlogn)
D. O ( n ) O(n) O(n)
正确答案:C
15、下列选项中,哪个不可能是下图的深度优先遍历序列( )。
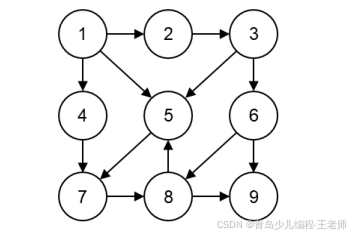
cpp
A. 2, 3, 5, 7, 8, 9, 6, 4, 1
B. 5, 7, 8, 9, 1, 2, 4, 3, 6
C. 6, 8, 9, 5, 7, 1, 2, 3, 4
D. 8, 5, 7, 9, 1, 2, 3, 6, 4正确答案:B
判断题(每题 2 分,共 20 分)
1、C++语言中,表达式 9 && 12 的结果类型为 int 、值为 8 。
正确答案:错误
2、 C++语言中,在有 int a[10]; 定义的范围内,通过表达式 a[-1] 进行访问将导致编译错误。
正确答案:错误
3、选择排序一般是不稳定的。
正确答案:正确
4、C++语言中, float 和 int 类型一般都是 4 字节,因此 float 类型能够表达不同的浮点数值的数量,与int 类型能够表达不同的整数值的数量是相同的。
正确答案:错误
5、使用 math.h 或 cmath 头文件中的对数函数,表达式 log(256) 的结果类型为 double 、值约为 8.0 。
正确答案:错误
6、一棵有N个节点的完全二叉树,则树的深度为 ⌊ l o g 2 ( N ) ⌋ + 1 \lfloor log_2(N) \rfloor + 1 ⌊log2(N)⌋+1。( )
正确答案:正确
7、邻接表和邻接矩阵都是图的存储形式。通常,使用邻接表比使用邻接矩阵的时间复杂度更低。
正确答案:错误
8、 C++语言中,类的构造函数可以声明为私有(private)。
正确答案:正确
9、泛洪算法的递归实现容易造成溢出,因此大的二维地图算法中,一般使用广度优先搜索实现。
正确答案:正确
10、很多游戏中为玩家设置多种可供学习的技能,要学习特定技能又往往需要先学习1个或以上的前置技能。尽管这样的技能间依赖关系常被玩家称为"技能树",但它并不一定是树,更可能是有向无环图。
正确答案:正确
编程题 (每题 25 分,共 50 分)
连通图
【问题描述】
给定一张包含n个结点与m条边的无向图,结点依次以1,2,...,n编号,第i条边 ( 1 ≤ i ≤ m ) (1 \le i \le m) (1≤i≤m)连接结点 u i u_i ui与结点 v i v_i vi。如果从一个结点经过若干条边可以到达另一个结点,则称这两个结点是连通的。
你需要向图中加入若干条边,使得图中任意两个结点都是连通的。请你求出最少需要加入的边的条数。
注意给出的图中可能包含重边与自环。
【输入格式】
第一行,两个正整数n, m,表示图的点数与边数。
接下来m行,每行两个正整数 u i , v i u_i,v_i ui,vi,表示图中一条连接结点 u i u_i ui与结点 v i v_i vi的边。
【输出格式】
输出一行,一个整数,表示使得图中任意两个结点连通所需加入的边的最少数量。
【样例输入 1】
4 4
1 2
2 3
3 1
1 4
【样例输出 1】
0
【样例输入 2】
6 4
1 2
2 3
3 1
6 5
【样例输出 2】
2
【数据范围】
对于40% 的测试点,保证 1 ≤ n ≤ 100 , 1 ≤ m ≤ 100 1 \le n \le 100, 1 \le m \le 100 1≤n≤100,1≤m≤100。
对于所有测试点,保证 1 ≤ n ≤ 1 0 5 , 1 ≤ m ≤ 1 0 5 1 \le n \le 10^5, 1 \le m \le 10^5 1≤n≤105,1≤m≤105。
金币收集
【问题描述】
小 A 正在游玩收集金币的游戏。具体来说,在数轴上将会出现n枚金币,其中第i枚 ( 1 ≤ i ≤ n ) (1 \le i \le n) (1≤i≤n)金币将会在时刻 t i t_i ti出现在数轴上坐标为 x i x_i xi的位置。小 A 必须在时刻 t i t_i ti恰好位于坐标 x i x_i xi,才可以获得第i枚金币。
游戏开始时为时刻0,此时小 A 的坐标为0。正常来说,小 A 可以按游戏机的按键在数轴上左右移动,但不幸的是
游戏机的左方向键失灵了。小 A 每个时刻只能选择保持不动,或是向右移动一个单位。换言之,如果小 A 在时刻t的坐标为x,那么他在时刻t+1的坐标只能是x或是x+1二者之一,分别对应保持不动和向右移动。
小 A 想知道他最多能收集多少枚金币。你能帮他收集最多的金币吗?
【输入格式】
第一行,一个正整数n,表示金币的数量。
接下来n行,每行两个正整数 x i , t i x_i, t_i xi,ti,分别表示金币出现的坐标与时刻。
【输出格式】
输出一行,一个整数,表示小 A 最多能收集的金币数量。
【样例输入 1】
3
1 6
3 7
2 4
【样例输出 1】
2
【样例输入 2】
4
1 1
2 2
1 3
2 4
【样例输出 2】
3
【数据范围】
对于40% 的测试点,保证 1 ≤ n ≤ 8 1 \le n \le 8 1≤n≤8。
对于另外30% 的测试点,保证 1 ≤ n ≤ 100 , 1 ≤ x i ≤ 100 , 1 ≤ t i ≤ 100 1 \le n \le 100, 1 \le x_i \le 100, 1 \le t_i \le 100 1≤n≤100,1≤xi≤100,1≤ti≤100。
对于所有测试点,保证 1 ≤ n ≤ 1 0 5 , 1 ≤ x i ≤ 1 0 9 , 1 ≤ t i ≤ 1 0 9 1 \le n \le 10^5, 1 \le x_i \le 10^9, 1 \le t_i \le 10^9 1≤n≤105,1≤xi≤109,1≤ti≤109。