目录
- [0 专栏介绍](#0 专栏介绍)
- [1 SAC算法回顾](#1 SAC算法回顾)
- [2 端到端SAC算法训练(Pytorch)](#2 端到端SAC算法训练(Pytorch))
- [3 基于SAC算法的动态避障](#3 基于SAC算法的动态避障)
0 专栏介绍
本专栏以贝尔曼最优方程等数学原理为根基,结合PyTorch框架逐层拆解DRL的核心算法(如DQN、PPO、SAC)逻辑。针对机器人运动规划场景,深入探讨如何将DRL与路径规划、动态避障等任务结合,包含仿真环境搭建、状态空间设计、奖励函数工程化调优等技术细节,旨在帮助读者掌握深度强化学习技术在机器人运动规划中的实战应用
1 SAC算法回顾
在深度强化学习 | 图文详细推导软性演员-评论家SAC算法原理中,我们介绍过**软性演员-评论家(Soft Actor-Critic, SAC)的核心原理就是在演员-评论家(Actor-Critic, AC)**框架下,优化带有最大熵正则项的策略网络,即优化
-
参数化动作-价值函数 (Critic)
J ( w ) = 1 2 E [ ( Q ( s , a ; w ) − ( r s → s ′ + γ max a ′ ( Q ^ ( s ′ , a ′ ; w ^ ) − α log π ( s ′ , a ′ ; θ ) ) ) ) ] J\left( \boldsymbol{w} \right) =\frac{1}{2}\mathbb{E} \left[ \left( Q\left( \boldsymbol{s},\boldsymbol{a};\boldsymbol{w} \right) -\left( r_{\boldsymbol{s}\rightarrow \boldsymbol{s}'}+\gamma \max _{\boldsymbol{a}'}\left( \hat{Q}\left( \boldsymbol{s}',\boldsymbol{a}';\boldsymbol{\hat{w}} \right) -\alpha \log \pi \left( \boldsymbol{s}',\boldsymbol{a}';\boldsymbol{\theta } \right) \right) \right) \right) \right] J(w)=21E[(Q(s,a;w)−(rs→s′+γa′max(Q^(s′,a′;w^)−αlogπ(s′,a′;θ))))] -
参数化策略 (Actor)
J ( θ ) = E ( s , a ) π ( α log π ( s , a ; θ ) − Q ( s , a ; w ) ) J\left( \boldsymbol{\theta } \right) =\mathbb{E} _{\left( \boldsymbol{s},\boldsymbol{a} \right) ~\pi}\left( \alpha \log \pi \left( \boldsymbol{s},\boldsymbol{a};\boldsymbol{\theta } \right) -Q\left( \boldsymbol{s},\boldsymbol{a};\boldsymbol{w} \right) \right) J(θ)=E(s,a) π(αlogπ(s,a;θ)−Q(s,a;w)) -
参数化温度
J ( α ) = E [ − α log π ( s , a ; θ ) − α H 0 ] J\left( \alpha \right) =\mathbb{E} \left[ -\alpha \log \pi \left( \boldsymbol{s},\boldsymbol{a};\boldsymbol{\theta } \right) -\alpha H_0 \right] J(α)=E[−αlogπ(s,a;θ)−αH0]
Actor通过与环境交互积累经验,Critic则基于这些经验更新对价值的估计,反过来为Actor的策略优化提供方向

SAC算法完整的流程如下所示

2 端到端SAC算法训练(Pytorch)
在强化学习的初始阶段,机器人的运动经常性地发生碰撞,需要不断收集经验,并在交互中获得奖励反馈
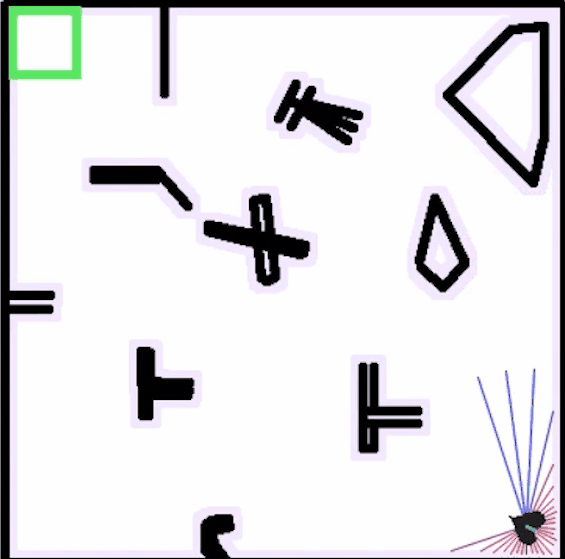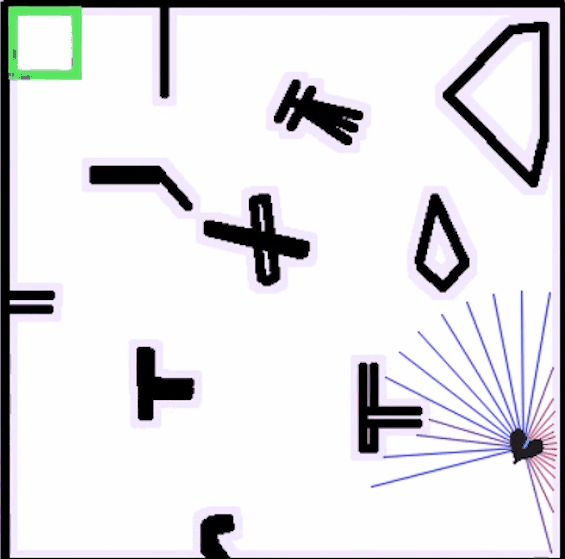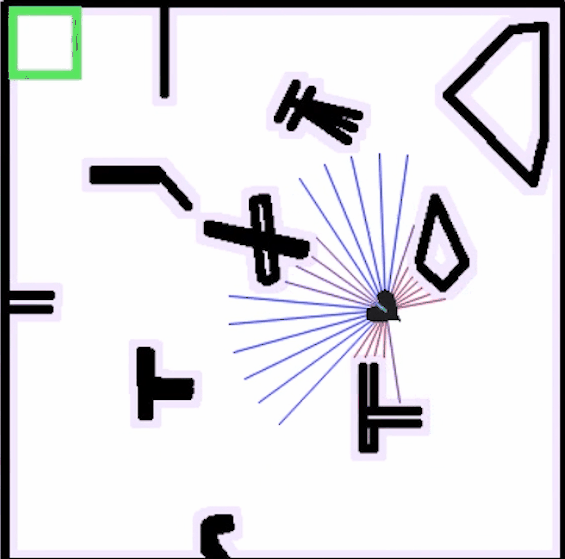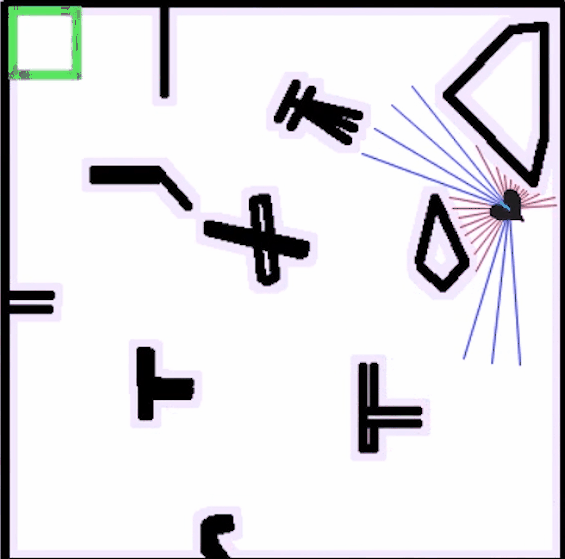
持续一段时间后,运动趋于稳定,机器人具备从起点无碰撞到达终点的能力
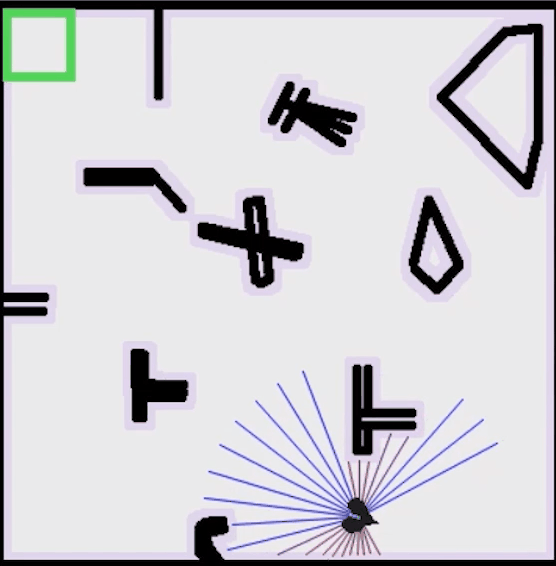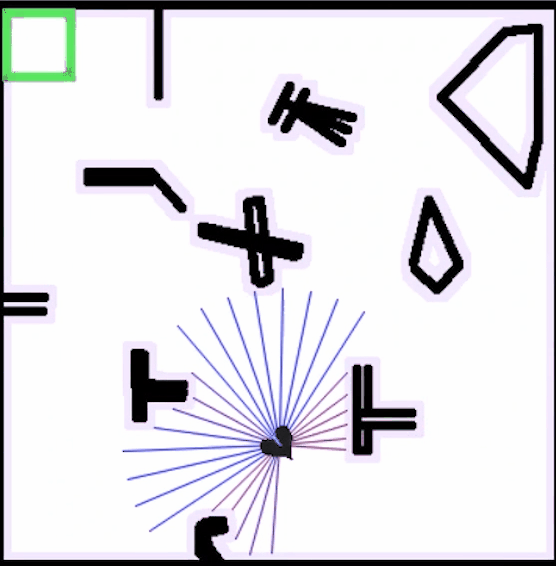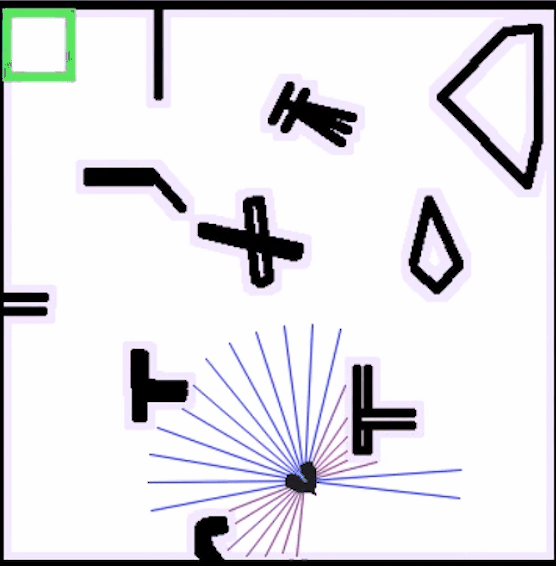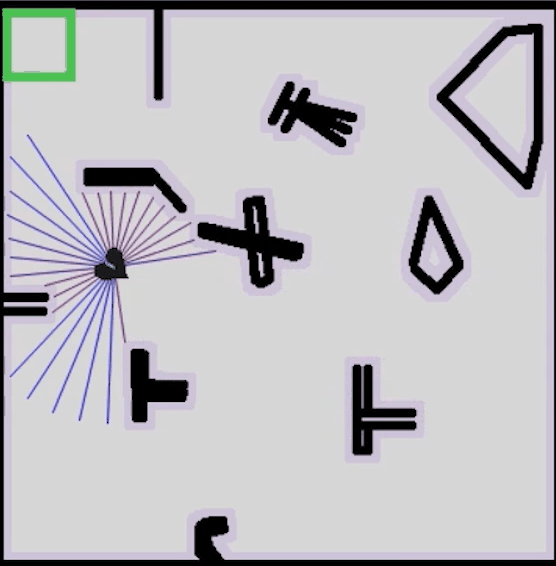
接着,我们简单测试以下训练好的权重的路径跟踪效果,采用以下控制器配置:
yaml
sac:
time_step: 0.1
max_iteration: 6500
lookahead_time: 1.5
min_lookahead_dist: 2.0
max_lookahead_dist: 3.5
min_v: 0.0
max_v: 1.0
min_w: -2.0
max_w: 2.0
min_v_inc: -1.0
max_v_inc: 1.0
min_w_inc: -1.0
max_w_inc: 1.0
goal_dist_tol: 0.5
rotate_tol: 0.5
use_gpu: True
policy:
n_critics: 2
share_feature_extractor: false
actor:
mlp_dims: !!python/list [32]
critic:
mlp_dims: !!python/list [128, 64]
feature_extractor:
mlp_dims: !!python/list [128, 256]
feature_dim: 128
lidar:
lidar_beams: 27
lidar_groups: 27
lidar_accuracy: 0.3
lidar_max_range: 10.0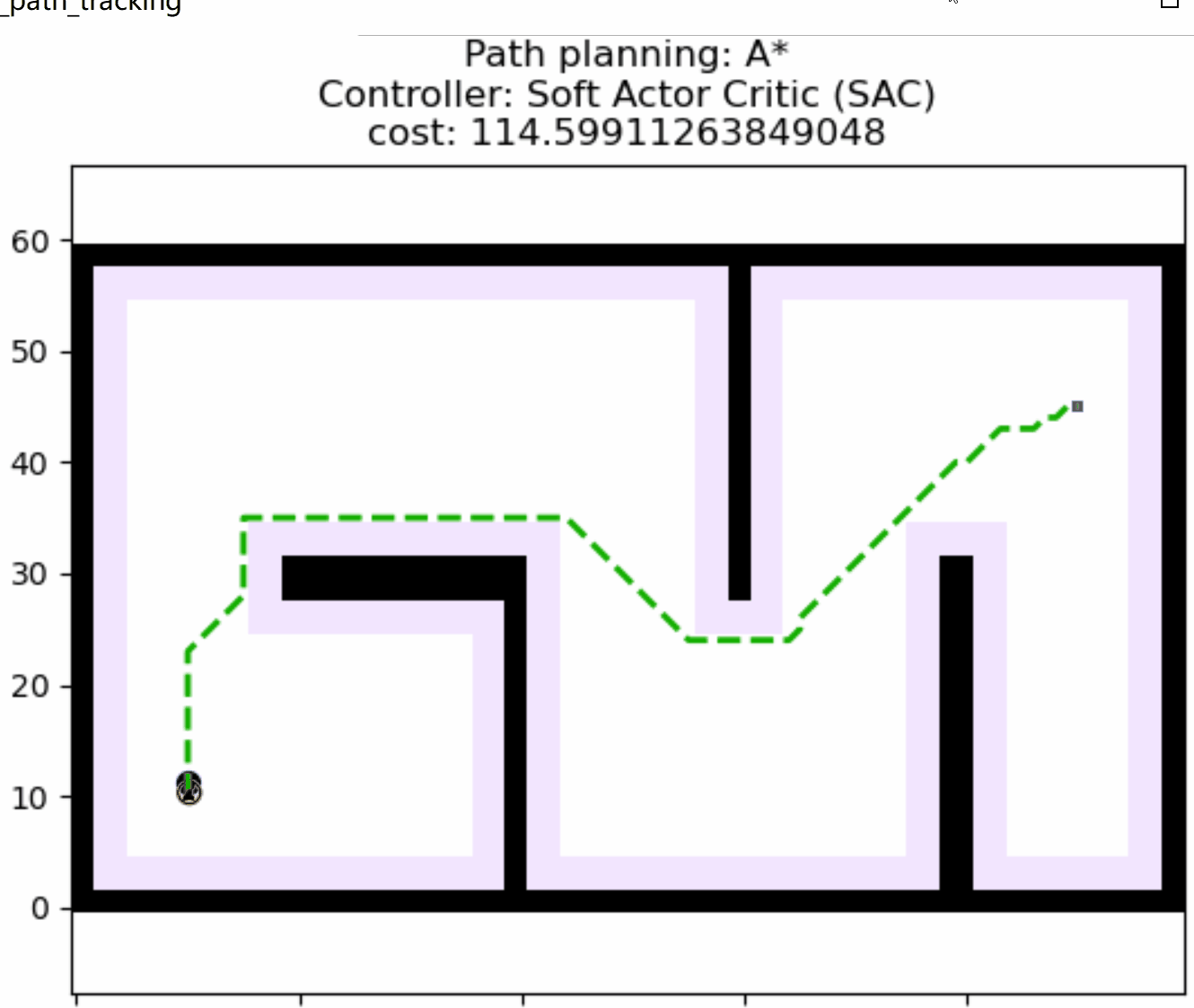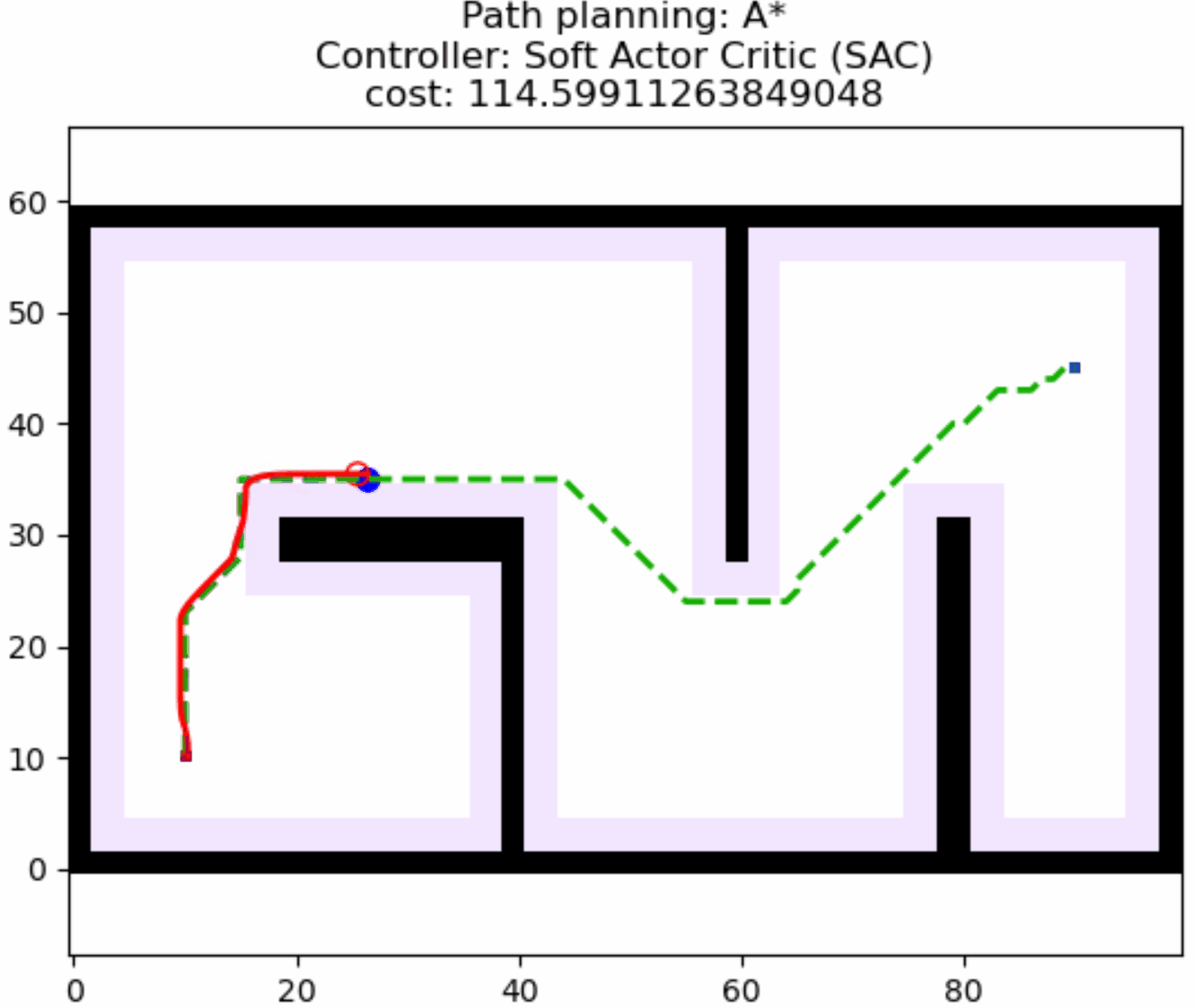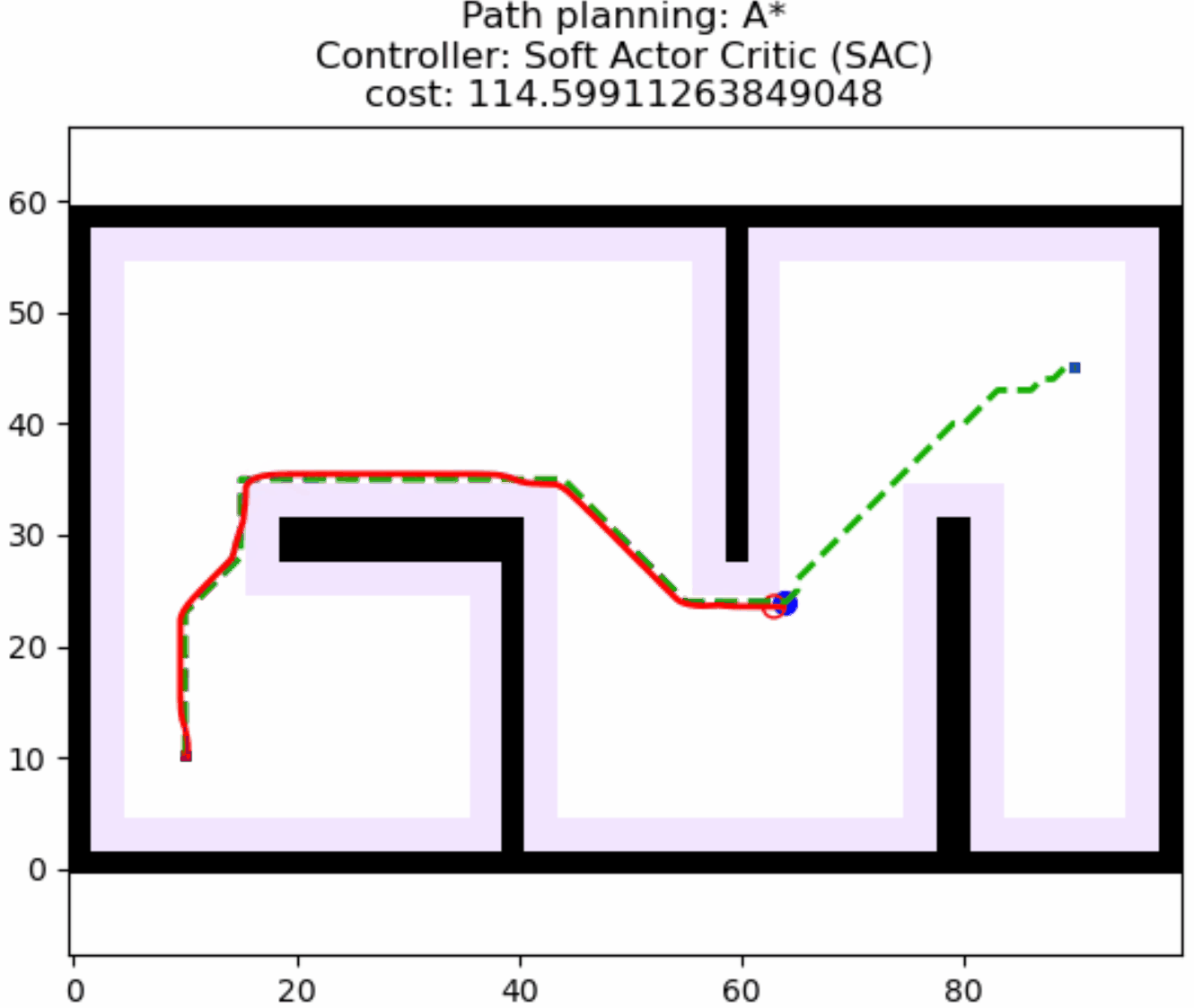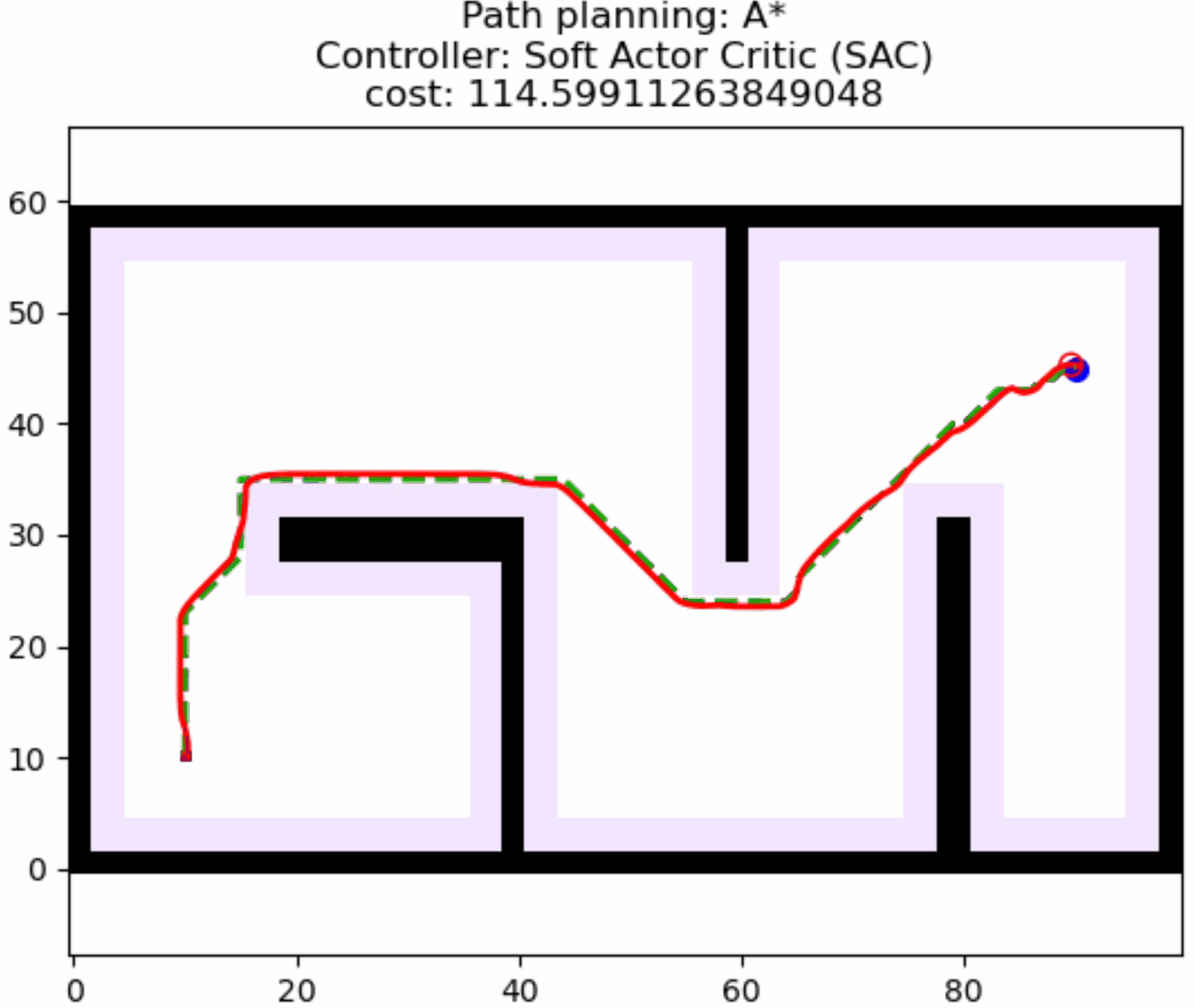
3 基于SAC算法的动态避障
核心代码如下所示:
cpp
bool SACController::_SACControl(const Point3d& s, const Point3d& s_d, double& v, double& w)
{
const double dx = s.x() - s_d.x();
const double dy = s.y() - s_d.y();
const double distance = std::hypot(dx, dy);
const double beta = M_PI / 2 - std::atan(dx / dy) + (dy > 0 ? M_PI : 0);
double alpha = (beta - s.theta()) / M_PI;
nav_msgs::Odometry base_odom;
odom_helper_->getOdom(base_odom);
double curr_v = std::hypot(base_odom.twist.twist.linear.x, base_odom.twist.twist.linear.y);
double curr_w = base_odom.twist.twist.angular.z;
std::vector<double> observation = { distance / 10.0, alpha, curr_v / 2.0, curr_w / 2.0 };
for (const auto& r : lidar_scans_grouped_)
{
observation.push_back(r / lidar_range_max_);
}
sac_controller::SACControl srv;
srv.request.observation = observation;
if (policy_client_.call(srv))
{
v = srv.response.v;
w = srv.response.w;
return true;
}
return false;
}
python
class SACServer:
def __init__(self) -> None:
device = torch.device("cuda" if torch.cuda.is_available() and self.params["use_gpu"] else "cpu")
self.policy = SACPolicy(
obs_dim=31,
action_dim=2,
device=device,
**self.params["policy"],
)
model_path = os.path.abspath(os.path.join(__file__, "../sac_policy/sac_model.pth"))
self.policy.load_state_dict(torch.load(model_path, map_location=device))
self.sac_service = rospy.Service('/sac_control', SACControl, self.SACFeedback)
def SACFeedback(self, req):
observation_tensor = torch.as_tensor(req.observation, device=self.policy.device).float()
self.policy.setTrainingMode(False)
with torch.no_grad():
actions = self.policy(observation_tensor, True).cpu().numpy().reshape(2,)
v = (float(actions[0]) + 1.0) * 0.5 * self.params["max_v"]
w = actions[1] * self.params["max_w"]
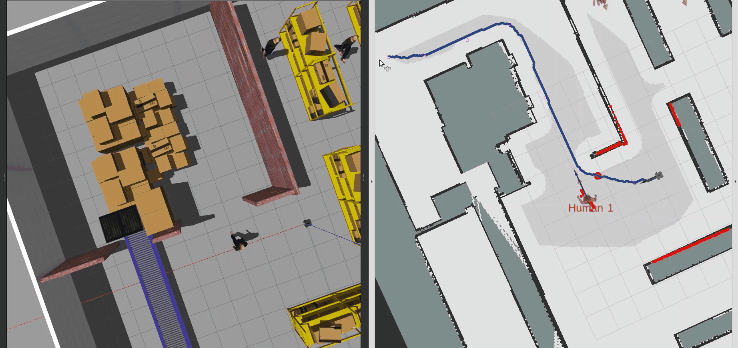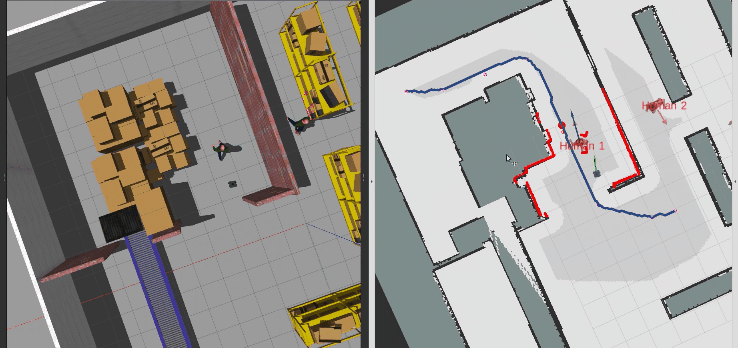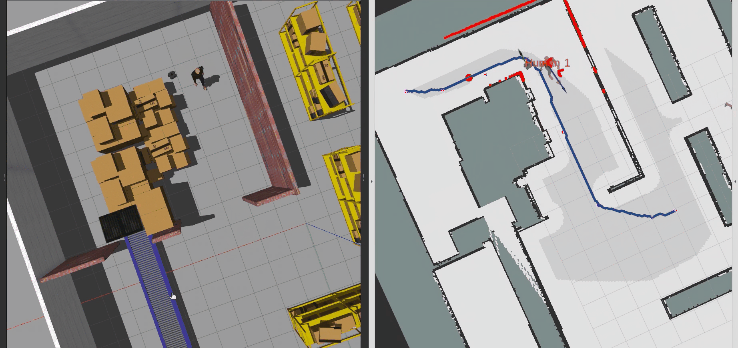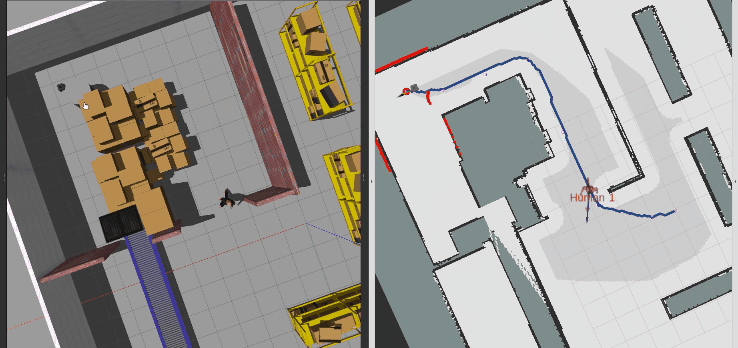
return SACControlResponse(v=v, w=w)指定一个目标位置,蓝色路径就是路径规划算法的结果,这里我们指定路径规划只规划一次,并在规划好的路径上随机放一点障碍,测试SAC的动态避障效果,可以看到机器人具备局部避障能力

接着,直接用动态行人作为动态障碍物,测试SAC算法的性能,可以看到机器人先是被行人压着速度,当存在避让空间时主动选择绕行
🔥 更多精彩专栏:
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇