算法奇妙屋(六)-哈希表

文章目录

• [一. 力扣 1. 两数之和](#一. 力扣 1. 两数之和)
• • [1. 题目](#1. 题目)
  • [2. 算法原理](#2. 算法原理)
  • • [(1) 暴力解法1, 2:](#(1) 暴力解法1, 2:)
    • [(2) 哈希解法:](#(2) 哈希解法:)
  • [3. 代码](#3. 代码)
  • • [(1) 暴力解法1, 2:](#(1) 暴力解法1, 2:)
    • [(2) 哈希解法:](#(2) 哈希解法:)
• [二. 力扣 面试题 01.02. 判定是否互为字符重排](#二. 力扣 面试题 01.02. 判定是否互为字符重排)
• • [1. 题目](#1. 题目)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [三. 力扣 217.存在重复元素](#三. 力扣 217.存在重复元素)
• • [1. 题目](#1. 题目)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [四. 力扣 219. 存在重复元素 II](#四. 力扣 219. 存在重复元素 II)
• • [1. 题目](#1. 题目)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)
• [五. 力扣 49. 字母异位词分组](#五. 力扣 49. 字母异位词分组)
• • [1. 题目](#1. 题目)
  • [2. 算法原理](#2. 算法原理)
  • [3. 代码](#3. 代码)

一. 力扣 1. 两数之和

1. 题目

提议十分简单,即求两数之和等于目标值的下标,并且下标不能出现两次

2. 算法原理

(1) 暴力解法1, 2:

1: 固定一个数,向后找
2: 固定一个数,向前找

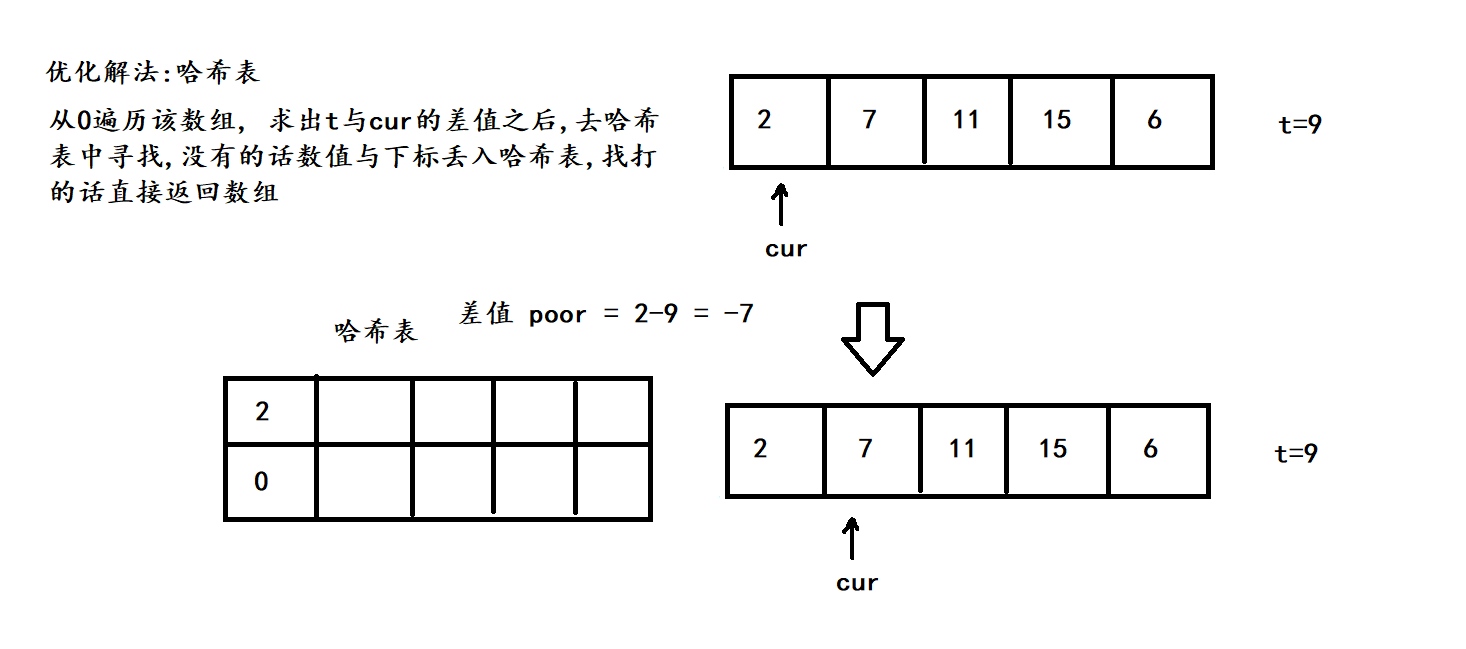
(2) 哈希解法:

3. 代码

(1) 暴力解法1, 2:

// 暴力解法 1
    public int[] twoSum(int[] nums, int target) {
        int n = nums.length;
        int[] ret = new int[2];
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (nums[i] + nums[j] == target) {
                    ret[0] = i;
                    ret[1] = j;
                    return ret;
                }
            }
        }
        return null;
    }

// 暴力解法 2
    public int[] twoSum(int[] nums, int target) {
        int n = nums.length;
        int[] ret = new int[2];
        for (int i = 1; i < n; i++) {
            for (int j = i - 1; j >= 0; j--) {
                if (nums[i] + nums[j] == target) {
                    ret[0] = i;
                    ret[1] = j;
                    return ret;
                }
            }
        }
        return null;
    }

(2) 哈希解法:

    public int[] twoSum(int[] nums, int target) {
        int[] ret = new int[2];
        Map<Integer,Integer> hash = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int pool = target - nums[i];
            int index = hash.getOrDefault(pool,-1);
            if ( index != -1) {
                ret[0] = index;
                ret[1] = i;
                return ret;
            }
            hash.put(nums[i], i);
        }
        return null;
    }

---

二. 力扣 面试题 01.02. 判定是否互为字符重排

1. 题目

这道题比较简单, 具体看题意即可

2. 算法原理

3. 代码

    public boolean CheckPermutation(String s1, String s2) {
        if (s1.length() != s2.length()) {
            return false;
        }
        int n = s1.length();
        int[] hash = new int[26];
        for (int i = 0; i < n; i++) {
            hash[s1.charAt(i) - 'a']++;
        }
        for (int i = 0; i < n; i++) {
            hash[s2.charAt(i) - 'a']--;
            if ((hash[s2.charAt(i) - 'a']) < 0) {
                return false;
            }
        }
        return true;
    }

---

三. 力扣 217.存在重复元素

1. 题目

2. 算法原理

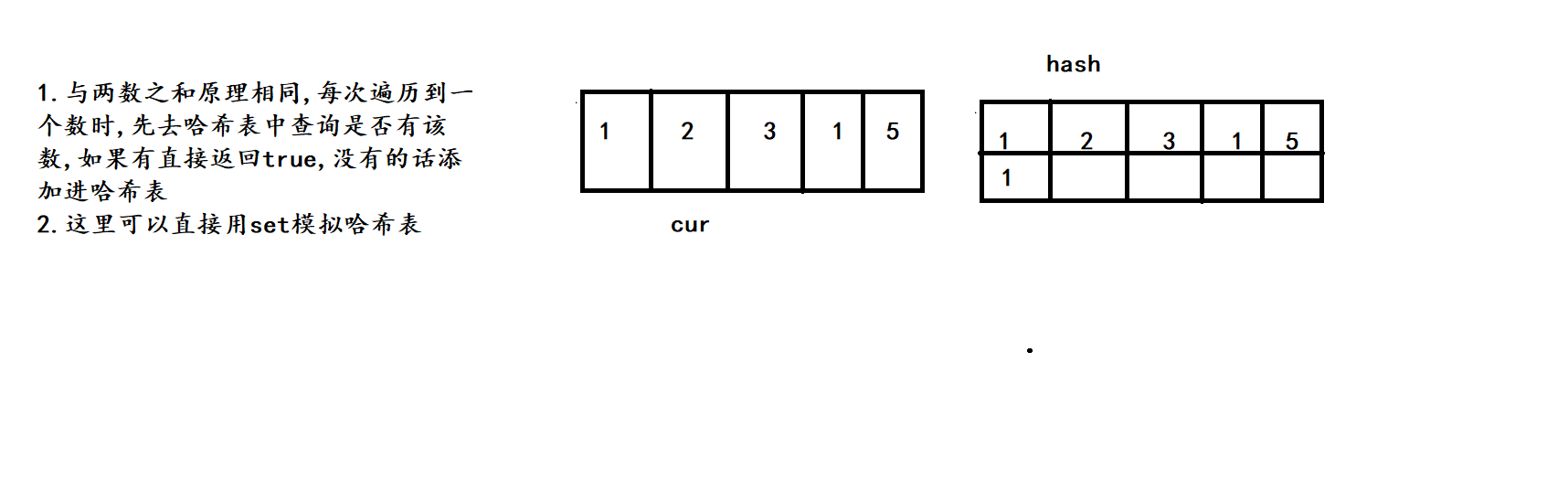
这里的算法原理十分简单, 用set模拟哈希表即可快速解决

3. 代码

    public boolean containsDuplicate(int[] nums) {
        Set<Integer> hash = new HashSet<>();
        for (int i = 0; i < nums.length; i++) {
            if (hash.contains(nums[i])) {
                return true;
            }
            hash.add(nums[i]);
        }
        return false;
    }

四. 力扣 219. 存在重复元素 II

1. 题目

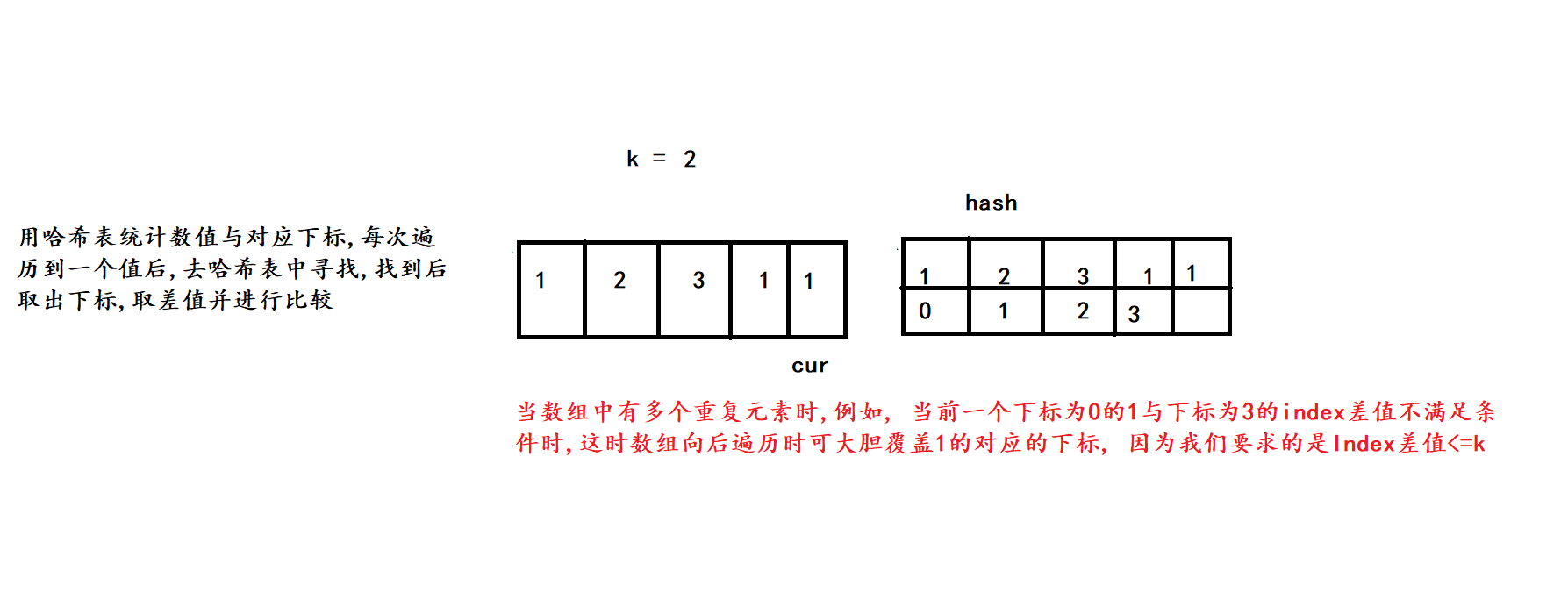
相比于上一道题只是增加了下标的差值<=k这个条件

2. 算法原理

3. 代码

    public boolean containsNearbyDuplicate(int[] nums, int k) {
        Map<Integer,Integer> hash = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int index = hash.getOrDefault(nums[i], -1);
            if (index != -1 && Math.abs(i - index) <= k) {
                return true;
            }
            hash.put(nums[i], i);
        }
        return false;
    }

五. 力扣 49. 字母异位词分组

1. 题目

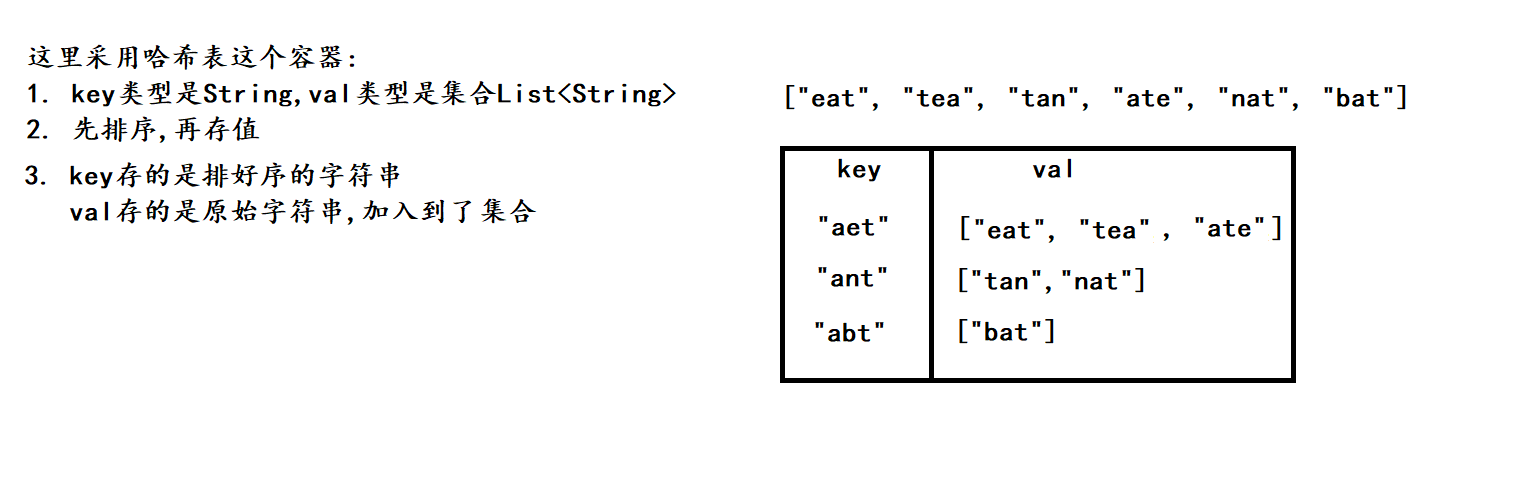
这道题有点像第二题的变种, 这里多了一步是将所有互为重排序的字符串放到一个集合

2. 算法原理

3. 代码

这里面需要注意的是, 排序后不可以直接使用toString将ch数组转为字符串, 这会导致字符串常量池无法存入, 导致值相同的字符串获取的的哈希地址不同, 会导致hash表中一个值对应多个val, 因为在哈希表中存入的string类型存的是哈希地址

    public List<List<String>> groupAnagrams(String[] strs) {
        List<List<String>> lists = new ArrayList<>();
        Map<String, List<String>> hash = new HashMap<>();
        for (String str : strs) {
            char[] ch = str.toCharArray();
            Arrays.sort(ch);
            String s = new String(ch);
            List<String> list = hash.getOrDefault(s, new ArrayList<>());
            list.add(str);
            hash.put(s,list);
        }
        return new ArrayList(hash.values());
    }