机器学习入门，无监督学习之K-Means聚类算法完全指南：面向Java开发者的Python实现详解

机器学习入门，无监督学习之K-Means聚类算法完全指南：面向Java开发者的Python实现详解

引言

作为一名Java开发者，你可能对面向对象编程和算法逻辑很熟悉，但Python在数据科学和机器学习领域的简洁语法和丰富库生态使其成为不可或缺的工具。本文将用Java开发者熟悉的视角，详细讲解K-Means聚类算法及其Python实现。

给Java开发者的Python快速参考

Java概念	Python对应	示例
List<String> list = new ArrayList<>()	list = []	colors = ['red', 'blue', 'green']
Map<String, Integer> map = new HashMap<>()	dict = {}	data = {'iteration': 1, 'centroids': [...]}
for (int i=0; i<10; i++)	for i in range(10):	循环语法
System.out.println()	print()	输出语句
class MyClass { ... }	class MyClass:	类定义

K-Means算法核心思想

K-Means是一种无监督学习算法，目标是将数据点自动分组到K个簇中。可以把它想象成：你有一堆混合的彩色球（数据点），要自动把它们按颜色分到K个篮子（簇）里，每个篮子的中心位置（质心）要能最好地代表这个篮子里的所有球。

算法步骤类比

1. 初始化：随机选择K个球作为初始篮子中心
2. 分配：把每个球放到离它最近的篮子中心对应的篮子
3. 更新：根据每个篮子里的球重新计算篮子中心位置
4. 迭代：重复2-3步，直到篮子中心不再移动

完整代码实现与详细解释

1. 环境准备和导入库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
import matplotlib.animation as animation

Java开发者需要了解的Python库：

• numpy ：相当于Java中的数值计算库，提供高效的数组操作
  • 类似：Java的Arrays + 数学计算库
• matplotlib ：绘图库，相当于Java的JFreeChart或JavaFX图表
• sklearn ：机器学习库，相当于Java的Weka或Smile
• animation：动画库，用于创建动态可视化

2. 数据生成模块

class KMeansVisualizer:
    """K-Means聚类可视化器"""
    
    def __init__(self, n_clusters=4, max_iter=10, random_state=42):
        # 构造函数，相当于Java的构造方法
        self.n_clusters = n_clusters      # 簇的数量K
        self.max_iter = max_iter          # 最大迭代次数
        self.random_state = random_state  # 随机种子（类似Java的Random种子）
        self.colors = ['red', 'blue', 'green', 'orange', 'purple', 'brown']
    
    def generate_sample_data(self, n_samples=300, centers=4, cluster_std=0.6, random_state=0):
        """生成示例数据"""
        # make_blobs生成模拟的聚类数据
        X, y_true = make_blobs(
            n_samples=n_samples,      # 样本数量
            centers=centers,          # 中心点数量
            cluster_std=cluster_std,  # 簇的标准差（控制分散程度）
            random_state=random_state # 随机种子
        )
        
        # 数据标准化：将数据缩放到均值为0，标准差为1
        # 类似Java中：(value - mean) / std
        scaler = StandardScaler()
        X_scaled = scaler.fit_transform(X)
        
        return X_scaled, y_true, scaler

Python语法详解：

• def __init__(self, ...): ：构造函数，self相当于Java的this
• def method_name(self, ...): ：实例方法，必须包含self参数
• 默认参数 ：n_samples=300 表示参数默认值，类似Java的方法重载
• 返回多个值：Python函数可以返回多个值，用逗号分隔

3. K-Means算法核心实现

class VisualKMeans:
    """可记录迭代过程的自定义K-Means实现"""
    
    def __init__(self, n_clusters=4, max_iter=10, random_state=42):
        self.n_clusters = n_clusters
        self.max_iter = max_iter
        self.random_state = random_state
        self.history = []  # 记录每次迭代的状态
        
    def fit(self, X):
        """训练K-Means模型并记录迭代过程"""
        # 设置随机种子，确保结果可重现
        np.random.seed(self.random_state)
        
        # 随机初始化质心：从数据中随机选择K个点作为初始质心
        # np.random.choice 类似：从数组中随机选择不重复的元素
        centroids = X[np.random.choice(len(X), self.n_clusters, replace=False)]
        
        # 开始迭代
        for iteration in range(self.max_iter):
            # 步骤1：计算每个点到质心的距离
            # 这里使用了NumPy的广播机制，避免写循环
            distances = np.sqrt(((X - centroids[:, np.newaxis])**2).sum(axis=2))
            
            # 为每个点分配最近的质心标签
            # np.argmin 返回最小值的索引
            labels = np.argmin(distances, axis=0)
            
            # 记录当前迭代状态（用于可视化）
            self.history.append({
                'iteration': iteration + 1,
                'centroids': centroids.copy(),  # copy()防止引用问题
                'labels': labels.copy()
            })
            
            # 步骤2：更新质心位置
            # 对每个簇，计算其所有点的平均值作为新质心
            new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(self.n_clusters)])
            
            # 检查收敛：如果质心基本不变，提前结束
            if np.allclose(centroids, new_centroids):
                break
                
            centroids = new_centroids  # 更新质心
            
        # 保存最终结果
        self.labels_ = labels
        self.cluster_centers_ = centroids
        return self  # 返回自身，支持链式调用

关键算法步骤的Java类比：

距离计算（Python向量化操作 vs Java循环）

Python向量化方式：

distances = np.sqrt(((X - centroids[:, np.newaxis])**2).sum(axis=2))

等价的Java伪代码：

// 假设：X是double[n][2]，centroids是double[k][2]
double[][] distances = new double[k][n];
for (int i = 0; i < k; i++) {
    for (int j = 0; j < n; j++) {
        double dx = X[j][0] - centroids[i][0];
        double dy = X[j][1] - centroids[i][1];
        distances[i][j] = Math.sqrt(dx*dx + dy*dy);
    }
}

标签分配

Python方式：

labels = np.argmin(distances, axis=0)

等价的Java伪代码：

int[] labels = new int[n];
for (int j = 0; j < n; j++) {
    int minIndex = 0;
    double minDist = distances[0][j];
    for (int i = 1; i < k; i++) {
        if (distances[i][j] < minDist) {
            minDist = distances[i][j];
            minIndex = i;
        }
    }
    labels[j] = minIndex;
}

更新质心位置

Python方式：

new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(self.n_clusters)])

等价的Java伪代码：

// 假设的数据结构：
// double[][] X;          // 数据矩阵 [n_samples][n_features]
// int[] labels;          // 标签数组 [n_samples]  
// int n_clusters;        // 簇的数量
// int n_samples;         // 样本总数
// int n_features;        // 特征数量

// 创建新质心数组
double[][] newCentroids = new double[n_clusters][n_features];

// 遍历每个簇
for (int clusterId = 0; clusterId < n_clusters; clusterId++) {
    
    // 统计当前簇的样本数量和特征总和
    int clusterSize = 0;
    double[] featureSums = new double[n_features];  // 存储每个特征的总和
    
    // 遍历所有样本，找出属于当前簇的样本
    for (int sampleId = 0; sampleId < n_samples; sampleId++) {
        if (labels[sampleId] == clusterId) {
            clusterSize++;
            // 累加每个特征的值
            for (int featureId = 0; featureId < n_features; featureId++) {
                featureSums[featureId] += X[sampleId][featureId];
            }
        }
    }
    
    // 计算平均值（新质心）
    if (clusterSize > 0) {
        for (int featureId = 0; featureId < n_features; featureId++) {
            newCentroids[clusterId][featureId] = featureSums[featureId] / clusterSize;
        }
    } else {
        // 处理空簇情况（没有样本属于该簇）
        // 策略1：设置为零向量
        for (int featureId = 0; featureId < n_features; featureId++) {
            newCentroids[clusterId][featureId] = 0.0;
        }
        // 策略2：随机选择一个数据点作为新质心
        // int randomIndex = (int)(Math.random() * n_samples);
        // newCentroids[clusterId] = Arrays.copyOf(X[randomIndex], n_features);
    }
}

4. 可视化模块

class KMeansPlotter:
    """K-Means结果绘图器"""
    
    def __init__(self, colors=None):
        # 如果未提供颜色，使用默认颜色列表
        self.colors = colors or ['red', 'blue', 'green', 'orange', 'purple', 'brown']
    
    def plot_iterations_grid(self, history, X, cols=3):
        """绘制迭代过程的网格图"""
        n_iterations = len(history)
        # 计算需要的行数：(总数 + 列数 - 1) // 列数
        rows = (n_iterations + cols - 1) // cols
        
        # 创建子图：plt.subplots 创建多个坐标轴
        fig, axes = plt.subplots(rows, cols, figsize=(15, 5 * rows))
        
        # 如果只有一行，调整axes的形状
        if rows == 1:
            axes = axes.reshape(1, -1)  # reshape改变数组形状
        
        # 遍历所有迭代状态
        for idx, state in enumerate(history):
            # 计算当前子图的位置
            row = idx // cols  # 整除求行
            col = idx % cols   # 取余求列
            
            # 获取对应的坐标轴对象
            ax = axes[row, col] if rows > 1 else axes[col]
            
            # 绘制单次迭代
            self._plot_single_iteration(ax, state, X, history, idx)
        
        # 隐藏多余的子图
        for idx in range(n_iterations, rows * cols):
            row = idx // cols
            col = idx % cols
            ax = axes[row, col] if rows > 1 else axes[col]
            ax.axis('off')  # 关闭坐标轴显示
        
        plt.tight_layout()  # 自动调整子图间距
        plt.show()          # 显示图形
    
    def _plot_single_iteration(self, ax, state, X, history, idx):
        """绘制单次迭代的结果"""
        iteration = state['iteration']
        centroids = state['centroids']
        labels = state['labels']
        
        # 绘制每个簇的数据点
        for cluster_id in range(len(centroids)):
            # 选择属于当前簇的所有点
            cluster_points = X[labels == cluster_id]
            
            # 绘制散点图
            ax.scatter(
                cluster_points[:, 0],   # x坐标
                cluster_points[:, 1],   # y坐标
                c=self.colors[cluster_id],  # 颜色
                alpha=0.6,              # 透明度
                s=50,                   # 点的大小
                label=f'Cluster {cluster_id+1}'  # 图例标签
            )
        
        # 绘制质心（用黑色X标记）
        ax.scatter(
            centroids[:, 0], centroids[:, 1], 
            marker='x',          # 标记形状为X
            s=200,               # 大小
            linewidths=3,        # 线宽
            color='black',       # 颜色
            label='Centroids',   # 图例标签
            zorder=5             # 绘制层级（确保在最上层）
        )
        
        # 绘制质心移动轨迹（从第二次迭代开始）
        if iteration > 1:
            prev_centroids = history[idx-1]['centroids']  # 前一次迭代的质心
            for i in range(len(centroids)):
                # 绘制从前一个位置到当前位置的线段
                ax.plot(
                    [prev_centroids[i, 0], centroids[i, 0]],  # x坐标
                    [prev_centroids[i, 1], centroids[i, 1]],  # y坐标
                    'k--',           # 黑色虚线
                    alpha=0.5,       # 透明度
                    linewidth=1      # 线宽
                )
        
        # 设置子图标题和标签
        ax.set_title(f'Iteration {iteration}')
        ax.set_xlabel('Feature 1')
        ax.set_ylabel('Feature 2')
        ax.grid(True, alpha=0.3)  # 显示网格
        
        # 只在第一个子图显示图例
        if idx == 0:
            ax.legend()

Python可视化概念解释：

• plt.subplots() ：创建图形和子图，返回(figure, axes_array)
• ax.scatter()：在指定坐标轴上绘制散点图
• ax.plot()：绘制线图
• ax.set_title() / ax.set_xlabel()：设置标题和坐标轴标签
• ax.legend()：显示图例
• plt.tight_layout()：自动调整子图间距
• plt.show()：显示图形

5. 动画创建模块

def create_animation(self, history, X, figsize=(10, 8)):
    """创建K-Means聚类过程的动画"""
    # 创建图形和坐标轴
    fig, ax = plt.subplots(figsize=figsize)
    
    def animate(frame):
        """动画的每一帧"""
        ax.clear()  # 清除上一帧
        state = history[frame]  # 获取当前帧对应的状态
        iteration = state['iteration']
        centroids = state['centroids']
        labels = state['labels']
        
        # 绘制数据点（与静态图相同的逻辑）
        for cluster_id in range(len(centroids)):
            cluster_points = X[labels == cluster_id]
            ax.scatter(
                cluster_points[:, 0], cluster_points[:, 1], 
                c=self.colors[cluster_id], alpha=0.6, s=50, 
                label=f'Cluster {cluster_id+1}'
            )
        
        # 绘制质心
        ax.scatter(
            centroids[:, 0], centroids[:, 1], 
            marker='x', s=200, linewidths=3, color='black', 
            label='Centroids', zorder=5
        )
        
        # 绘制质心移动轨迹
        if iteration > 1:
            prev_centroids = history[frame-1]['centroids']
            for i in range(len(centroids)):
                ax.plot(
                    [prev_centroids[i, 0], centroids[i, 0]], 
                    [prev_centroids[i, 1], centroids[i, 1]], 
                    'k--', alpha=0.5, linewidth=2
                )
        
        # 设置标题和标签
        ax.set_title(f'K-Means Clustering - Iteration {iteration}')
        ax.set_xlabel('Feature 1')
        ax.set_ylabel('Feature 2')
        ax.grid(True, alpha=0.3)
        ax.legend()
        
        return ax
    
    # 创建动画对象
    anim = animation.FuncAnimation(
        fig,           # 图形对象
        animate,       # 动画函数
        frames=len(history),  # 总帧数
        interval=1000,        # 帧间隔（毫秒）
        repeat=True           # 循环播放
    )
    plt.close()  # 关闭图形，避免重复显示
    return anim

动画技术说明：

• FuncAnimation：创建基于函数的动画
• frames：动画的总帧数，等于迭代次数
• interval：每帧之间的时间间隔（毫秒）
• repeat：是否循环播放动画

6. 结果分析模块

class KMeansAnalyzer:
    """K-Means结果分析器"""
    
    @staticmethod
    def evaluate_clustering(X, labels, true_labels=None):
        """评估聚类结果"""
        # 计算轮廓系数：衡量聚类质量的指标
        # 取值范围[-1, 1]，值越大表示聚类效果越好
        silhouette = silhouette_score(X, labels)
        
        print("聚类效果评估:")
        print(f"轮廓系数: {silhouette:.3f}")
        
        # 如果有真实标签，计算调整兰德指数
        if true_labels is not None:
            from sklearn.metrics import adjusted_rand_score
            # 调整兰德指数：比较聚类结果与真实标签的相似度
            ari = adjusted_rand_score(true_labels, labels)
            print(f"调整兰德指数: {ari:.3f}")
    
    @staticmethod
    def plot_convergence(history, X):
        """绘制收敛曲线"""
        inertia_history = []
        # 计算每次迭代的簇内平方和
        for state in history:
            centroids = state['centroids']
            labels = state['labels']
            inertia = KMeansAnalyzer._calculate_inertia(X, centroids, labels)
            inertia_history.append(inertia)
        
        # 绘制收敛曲线
        plt.figure(figsize=(10, 4))
        plt.plot(range(1, len(inertia_history)+1), inertia_history, 'go-')
        plt.xlabel('Iteration')
        plt.ylabel('Inertia')
        plt.title('Inertia Convergence')
        plt.grid(True, alpha=0.3)
        plt.show()
    
    @staticmethod
    def _calculate_inertia(X, centroids, labels):
        """计算簇内平方和（每个点到其质心距离的平方和）"""
        inertia = 0
        for i in range(len(centroids)):
            cluster_points = X[labels == i]
            if len(cluster_points) > 0:
                # 计算该簇所有点到质心的距离平方和
                inertia += np.sum((cluster_points - centroids[i])**2)
        return inertia

评估指标说明：

• 轮廓系数 (Silhouette Score)：衡量聚类紧密度和分离度的综合指标
• 调整兰德指数 (Adjusted Rand Index)：比较聚类结果与真实标签的一致性
• 簇内平方和 (Inertia)：每个点到其所属质心距离的平方和，值越小表示聚类越紧密

7. 完整流程演示

def main():
    """主函数 - 演示完整的K-Means聚类可视化流程"""
    
    # 1. 初始化各个组件
    visualizer = KMeansVisualizer(n_clusters=4, max_iter=10, random_state=42)
    plotter = KMeansPlotter()
    analyzer = KMeansAnalyzer()
    
    # 2. 生成示例数据
    X_scaled, y_true, scaler = visualizer.generate_sample_data()
    print(f"生成数据形状: {X_scaled.shape}")
    
    # 3. 训练K-Means模型
    vkmeans = visualizer.create_custom_kmeans()
    vkmeans.fit(X_scaled)
    
    # 4. 可视化迭代过程
    print("正在生成迭代过程可视化...")
    plotter.plot_iterations_grid(vkmeans.history, X_scaled)
    
    # 5. 创建动画
    print("正在生成动画...")
    anim = plotter.create_animation(vkmeans.history, X_scaled)
    
    # 6. 评估聚类结果
    analyzer.evaluate_clustering(X_scaled, vkmeans.labels_, y_true)
    analyzer.plot_convergence(vkmeans.history, X_scaled)
    
    # 7. 输出摘要信息
    print(f"\n聚类过程摘要:")
    print(f"总共进行了 {len(vkmeans.history)} 次迭代")
    print(f"最终轮廓系数: {silhouette_score(X_scaled, vkmeans.labels_):.3f}")
    
    return vkmeans, anim

# 运行主程序
if __name__ == "__main__":
    kmeans_model, animation_obj = main()

K-Means算法的重要特性

优点（从Java开发者角度）

1. 算法简单：逻辑清晰，易于理解和实现
2. 计算高效：时间复杂度为O(n×K×I×d)，适合处理大数据集
3. 可解释性强：聚类结果直观易懂
4. 广泛应用：客户分群、图像分割、异常检测等

局限性和应对策略

1. 需要预设K值 → 使用肘部法则选择最佳K值
2. 对初始值敏感 → 多次运行取最优结果
3. 对异常值敏感 → 数据预处理时处理异常值
4. 只能发现球状簇 → 对于复杂形状使用其他算法

如何选择K值（肘部法则）

def find_optimal_k(X, max_k=10):
    """使用肘部法则寻找最佳K值"""
    inertias = []
    k_range = range(1, max_k+1)
    
    for k in k_range:
        kmeans = KMeans(n_clusters=k, random_state=42)
        kmeans.fit(X)
        inertias.append(kmeans.inertia_)  # 簇内平方和
    
    # 绘制肘部图：寻找拐点
    plt.plot(k_range, inertias, 'bo-')
    plt.xlabel('Number of Clusters (K)')
    plt.ylabel('Inertia')
    plt.title('Elbow Method for Optimal K')
    plt.show()

实际应用场景

1. 客户细分：根据购买行为将客户分组，制定精准营销策略
2. 文档分类：自动将文档按主题分组
3. 图像压缩：将相似颜色的像素分组，减少颜色数量
4. 异常检测：识别与其他数据点显著不同的点
5. 社交网络分析：发现社区结构

给Java开发者的学习建议

Python与Java的主要差异

1. 语法简洁：Python使用缩进代替大括号，代码更简洁
2. 动态类型：变量不需要声明类型
3. 丰富的科学计算库：NumPy、Pandas、Matplotlib等
4. 交互式开发：Jupyter Notebook支持即时反馈

下一步学习路径

1. 掌握NumPy：Python的数值计算基础
2. 学习Pandas：数据处理和分析
3. 了解Scikit-learn：机器学习算法库
4. 实践项目：从简单分类、回归问题开始

总结

通过本文的详细讲解，作为Java开发者的你应该已经：

1. 理解了K-Means算法的核心原理和实现步骤
2. 掌握了Python在数据科学中的基本语法和库使用
3. 学会了如何可视化机器学习算法的迭代过程
4. 了解了聚类结果的评估方法和质量指标

K-Means算法虽然简单，但它体现了机器学习中的许多重要概念：迭代优化、距离度量、聚类评估等。掌握这个算法为你学习更复杂的机器学习技术奠定了坚实基础。

记住，从Java转向Python最重要的是理解两者的思维差异：Java强调严谨的类型系统和面向对象设计，Python更注重开发效率和简洁表达。在数据科学领域，Python的简洁语法和丰富库生态确实提供了巨大优势。

附：聚类效果

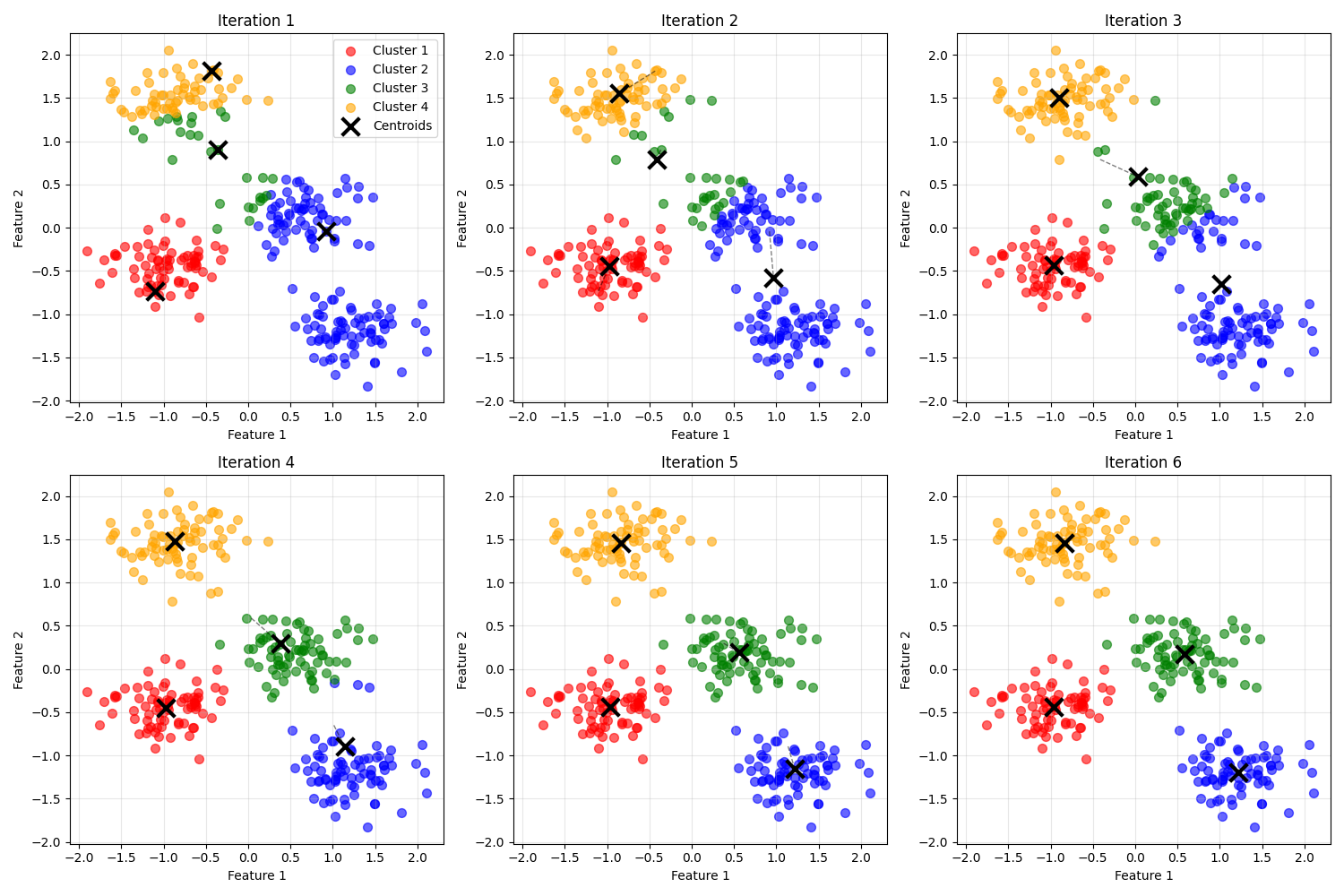
附：完整的kmeans测试代码示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
import matplotlib.animation as animation
from IPython.display import HTML


class KMeansVisualizer:
    """K-Means聚类可视化器"""

    def __init__(self, n_clusters=4, max_iter=10, random_state=42):
        self.n_clusters = n_clusters
        self.max_iter = max_iter
        self.random_state = random_state
        self.colors = ['red', 'blue', 'green', 'orange', 'purple', 'brown']

    def generate_sample_data(self, n_samples=300, centers=4, cluster_std=0.6, random_state=0):
        """生成示例数据"""
        X, y_true = make_blobs(
            n_samples=n_samples,
            centers=centers,
            cluster_std=cluster_std,
            random_state=random_state
        )

        # 数据标准化
        scaler = StandardScaler()
        X_scaled = scaler.fit_transform(X)

        return X_scaled, y_true, scaler

    def create_custom_kmeans(self):
        """创建自定义K-Means实例"""
        return VisualKMeans(
            n_clusters=self.n_clusters,
            max_iter=self.max_iter,
            random_state=self.random_state
        )


class VisualKMeans:
    """可记录迭代过程的自定义K-Means实现"""

    def __init__(self, n_clusters=4, max_iter=10, random_state=42):
        self.n_clusters = n_clusters
        self.max_iter = max_iter
        self.random_state = random_state
        self.history = []  # 记录每次迭代的状态

    def fit(self, X):
        """训练K-Means模型并记录迭代过程"""
        np.random.seed(self.random_state)

        # 随机初始化质心
        centroids = X[np.random.choice(len(X), self.n_clusters, replace=False)]

        for iteration in range(self.max_iter):
            # 计算每个点到质心的距离
            distances = np.sqrt(((X - centroids[:, np.newaxis]) ** 2).sum(axis=2))
            labels = np.argmin(distances, axis=0)

            # 记录当前状态
            self.history.append({
                'iteration': iteration + 1,
                'centroids': centroids.copy(),
                'labels': labels.copy()
            })

            # 更新质心
            new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(self.n_clusters)])

            # 检查收敛
            if np.allclose(centroids, new_centroids):
                break

            centroids = new_centroids

        self.labels_ = labels
        self.cluster_centers_ = centroids
        return self


class KMeansPlotter:
    """K-Means结果绘图器"""

    def __init__(self, colors=None):
        self.colors = colors or ['red', 'blue', 'green', 'orange', 'purple', 'brown']

    def plot_iterations_grid(self, history, X, cols=3):
        """绘制迭代过程的网格图"""
        n_iterations = len(history)
        rows = (n_iterations + cols - 1) // cols

        fig, axes = plt.subplots(rows, cols, figsize=(15, 5 * rows))
        if rows == 1:
            axes = axes.reshape(1, -1)

        for idx, state in enumerate(history):
            row = idx // cols
            col = idx % cols

            ax = axes[row, col] if rows > 1 else axes[col]
            self._plot_single_iteration(ax, state, X, history, idx)

        # 隐藏多余的子图
        for idx in range(n_iterations, rows * cols):
            row = idx // cols
            col = idx % cols
            ax = axes[row, col] if rows > 1 else axes[col]
            ax.axis('off')

        plt.tight_layout()
        plt.show()

    def _plot_single_iteration(self, ax, state, X, history, idx):
        """绘制单次迭代的结果"""
        iteration = state['iteration']
        centroids = state['centroids']
        labels = state['labels']

        # 绘制数据点
        for cluster_id in range(len(centroids)):
            cluster_points = X[labels == cluster_id]
            ax.scatter(
                cluster_points[:, 0], cluster_points[:, 1],
                c=self.colors[cluster_id], alpha=0.6, s=50,
                label=f'Cluster {cluster_id + 1}'
            )

        # 绘制质心
        ax.scatter(
            centroids[:, 0], centroids[:, 1],
            marker='x', s=200, linewidths=3, color='black',
            label='Centroids', zorder=5
        )

        # 绘制质心移动轨迹（如果不是第一次迭代）
        if iteration > 1:
            prev_centroids = history[idx - 1]['centroids']
            for i in range(len(centroids)):
                ax.plot(
                    [prev_centroids[i, 0], centroids[i, 0]],
                    [prev_centroids[i, 1], centroids[i, 1]],
                    'k--', alpha=0.5, linewidth=1
                )

        ax.set_title(f'Iteration {iteration}')
        ax.set_xlabel('Feature 1')
        ax.set_ylabel('Feature 2')
        ax.grid(True, alpha=0.3)

        # 只在第一个子图显示图例
        if idx == 0:
            ax.legend()

    def create_animation(self, history, X, figsize=(10, 8)):
        """创建K-Means聚类过程的动画"""
        fig, ax = plt.subplots(figsize=figsize)

        def animate(frame):
            ax.clear()
            state = history[frame]
            iteration = state['iteration']
            centroids = state['centroids']
            labels = state['labels']

            # 绘制数据点
            for cluster_id in range(len(centroids)):
                cluster_points = X[labels == cluster_id]
                ax.scatter(
                    cluster_points[:, 0], cluster_points[:, 1],
                    c=self.colors[cluster_id], alpha=0.6, s=50,
                    label=f'Cluster {cluster_id + 1}'
                )

            # 绘制质心
            ax.scatter(
                centroids[:, 0], centroids[:, 1],
                marker='x', s=200, linewidths=3, color='black',
                label='Centroids', zorder=5
            )

            # 绘制质心移动轨迹
            if iteration > 1:
                prev_centroids = history[frame - 1]['centroids']
                for i in range(len(centroids)):
                    ax.plot(
                        [prev_centroids[i, 0], centroids[i, 0]],
                        [prev_centroids[i, 1], centroids[i, 1]],
                        'k--', alpha=0.5, linewidth=2
                    )

            ax.set_title(f'K-Means Clustering - Iteration {iteration}')
            ax.set_xlabel('Feature 1')
            ax.set_ylabel('Feature 2')
            ax.grid(True, alpha=0.3)
            ax.legend()

            return ax

        anim = animation.FuncAnimation(
            fig, animate, frames=len(history),
            interval=1000, repeat=True
        )
        plt.close()
        return anim


class KMeansAnalyzer:
    """K-Means结果分析器"""

    @staticmethod
    def evaluate_clustering(X, labels, true_labels=None):
        """评估聚类结果"""
        silhouette = silhouette_score(X, labels)

        print("聚类效果评估:")
        print(f"轮廓系数: {silhouette:.3f}")

        if true_labels is not None:
            from sklearn.metrics import adjusted_rand_score
            ari = adjusted_rand_score(true_labels, labels)
            print(f"调整兰德指数: {ari:.3f}")

    @staticmethod
    def plot_convergence(history, X):
        """绘制收敛曲线"""
        inertia_history = []
        for state in history:
            centroids = state['centroids']
            labels = state['labels']
            inertia = KMeansAnalyzer._calculate_inertia(X, centroids, labels)
            inertia_history.append(inertia)

        plt.figure(figsize=(10, 4))
        plt.plot(range(1, len(inertia_history) + 1), inertia_history, 'go-')
        plt.xlabel('Iteration')
        plt.ylabel('Inertia')
        plt.title('Inertia Convergence')
        plt.grid(True, alpha=0.3)
        plt.show()

    @staticmethod
    def _calculate_inertia(X, centroids, labels):
        """计算簇内平方和"""
        inertia = 0
        for i in range(len(centroids)):
            cluster_points = X[labels == i]
            if len(cluster_points) > 0:
                inertia += np.sum((cluster_points - centroids[i]) ** 2)
        return inertia


def main():
    """主函数 - 演示完整的K-Means聚类可视化流程"""

    # 1. 初始化组件
    visualizer = KMeansVisualizer(n_clusters=4, max_iter=10, random_state=42)
    plotter = KMeansPlotter()
    analyzer = KMeansAnalyzer()

    # 2. 生成数据
    X_scaled, y_true, scaler = visualizer.generate_sample_data()
    print(f"生成数据形状: {X_scaled.shape}")

    # 3. 训练K-Means模型
    vkmeans = visualizer.create_custom_kmeans()
    vkmeans.fit(X_scaled)

    # 4. 可视化迭代过程
    print(f"正在生成迭代过程可视化... 迭代次数{len(vkmeans.history)}")
    plotter.plot_iterations_grid(vkmeans.history, X_scaled)

    # 5. 创建动画
    print("正在生成动画...")
    anim = plotter.create_animation(vkmeans.history, X_scaled)

    # 6. 评估结果
    analyzer.evaluate_clustering(X_scaled, vkmeans.labels_, y_true)
    analyzer.plot_convergence(vkmeans.history, X_scaled)

    # 7. 输出摘要
    print(f"\n聚类过程摘要:")
    print(f"总共进行了 {len(vkmeans.history)} 次迭代")
    print(f"最终轮廓系数: {silhouette_score(X_scaled, vkmeans.labels_):.3f}")

    # 可选：保存动画
    anim.save('kmeans_process.gif', writer='pillow', fps=1)
    print("动画已保存为 kmeans_process.gif")

    return vkmeans, anim


if __name__ == "__main__":
    # 运行主程序
    kmeans_model, animation_obj = main()

    # 在Jupyter中显示动画（取消注释以使用）
    html5_video = HTML(animation_obj.to_html5_video())
    print("html5_video \n",html5_video)