强化学习项目-3-CartPole-v1(AC)
环境
本环境是OpenAI Gym提供的一个经典控制环境。
官网链接:https://gymnasium.farama.org/environments/classic_control/cart_pole/
观测空间(状态S)
状态共包含 4 4 4个参数:
- 车位置(Cart Position)
- 车速(Cart Velocity)
- 杆子的角度(Pole Angle)
- 角速度(Pole Angular Velocity)
动作空间(动作A)
- 0: 推动车向左移动
- 1: 推动车向右移动
奖励
每坚持一步,环境将会给出 1 1 1点奖励,最大可以获得 500 500 500奖励,同时只要达到 200 200 200就视为达到通过门槛。
引入环境
下载包
text
pip install gymnasium导入
python
import gymnasium as gym
env = gym.make("CartPole-v1", render_mode="human")
# 获取状态维度和动作维度
state_dim = env.observation_space.shape[0] if len(env.observation_space.shape) == 1 else env.observation_space.n
action_dim = env.action_space.nAC算法(actor-critic)
区别于传统的 D Q N DQN DQN算法仅训练一个网络用于预测 Q ( s , a ) Q(s,a) Q(s,a), A C AC AC算法则分成两个网络:
- A c t o r Actor Actor : 针对状态 s s s,输出动作的概率分布
- C r i t i c Critic Critic : 价值估计器,这里采用 V ( s ) V(s) V(s),即从状态 s s s出发的期望奖励
Tips: V ( s ) = ∑ a i ∈ a c t i o n s V ( s i ′ ) × c i , c i 表示选择动作 a i V(s) = \sum\limits_{a_i \in actions} V(s_{i}^{\prime}) \times c_{i}, c_{i}\text{表示选择动作} a_{i} V(s)=ai∈actions∑V(si′)×ci,ci表示选择动作ai的概率, s i ′ s_{i}^{\prime} si′表示在状态 s s s选择动作 a i a_{i} ai到达的新状态
C r i t i c Critic Critic通过预测的 T D TD TD残差引导 A c t o r Actor Actor更新,而 C r i t i c Critic Critic则通过 T D TD TD目标更新
同时, A c t o r − C r i t i c Actor-Critic Actor−Critic的训练不能像 D Q N DQN DQN算法一样使用历史经验用于训练,每轮训练的数据仅使用本次模型与环境交互的全部数据
Actor网络
这里采用两层隐藏层,同时输出层采用Softmax激活函数,以预测状态 s s s下动作 a a a的概率分布
python
class Actor(nn.Module):
def __init__(self, hidden_dim = 128):
super(Actor, self).__init__()
self.net = nn.Sequential(
nn.Linear(state_dim, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, action_dim), nn.Softmax(dim=-1)
)
def forward(self, x):
return self.net(x)Critic网络
这里采用两层隐藏层,输出层无激活函数且仅包含一个神经元,用于预测 V ( s ) V(s) V(s)
python
class Critic(nn.Module):
def __init__(self, hidden_dim = 128):
super(Critic, self).__init__()
self.net = nn.Sequential(
nn.Linear(state_dim, hidden_dim),nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),nn.ReLU(),
nn.Linear(hidden_dim, 1)
)
def forward(self, x):
return self.net(x)Actor-Critic
初始化
A C AC AC算法的初始化较为简单,仅需初始化 A C AC AC两个神经网络,对应的优化器以及折扣因子即可
python
class ActorCritic():
def __init__(self, gamma):
self.actor = Actor().to(device)
self.critic = Critic().to(device)
self.optimizer_a = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.optimizer_c = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma动作选择
动作选择通过 A c t o r Actor Actor网络传入状态 s s s后预测得到概率分布后采样得到
python
def act(self, states):
states = torch.from_numpy(states).float().to(device)
with torch.no_grad():
probs = self.actor(states)
disk = torch.distributions.Categorical(probs)
return disk.sample().item()模型训练
先通过 C r i t i c Critic Critic网络预测的结果计算得到 T D TD TD目标以及 T D TD TD残差,然后分别计算得到两个网络的损失函数用于更新模型。
Tips:
- 这里为了计算更加稳定,对选择当前动作的概率取对数,同时为了避免当一个动作选择概率为 0 0 0时,此时取对数会出现无穷小 N a n Nan Nan的情况,计算时将概率加上 1 0 − 9 10^{-9} 10−9
- 对于表现好的动作(即 V ( s ′ ) V(s^{\prime}) V(s′)更大的动作),选择该动作的概率更高才能使得模型的表现更佳,因此 A c t o r Actor Actor网络采取的是梯度上升
python
def train(self, states, actions, rewards, next_states, dones):
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones)
td_delta = td_target - self.critic(states)
log_probs = torch.log(self.actor(states).gather(1, actions) + 1e-9)
actor_loss = torch.mean(-log_probs * td_delta.detach())
critic_loss = nn.functional.mse_loss(self.critic(states), td_target.detach())
self.optimizer_c.zero_grad()
self.optimizer_a.zero_grad()
critic_loss.backward()
actor_loss.backward()
self.optimizer_c.step()
self.optimizer_a.step()环境交互
这里与 D Q N DQN DQN不同的是,每轮都需要重新收集训练数据,且在本轮交互结束后才对模型进行训练。
Hint: 注意训练前要将数据转换为Tensor
python
torch.manual_seed(0)
actor_lr = 1e-4
critic_lr = 1e-3
gamma = 0.99
scores = []
episodes = 2000
model = ActorCritic(gamma)
from tqdm import tqdm
pbar = tqdm(range(episodes), desc="Training")
for episode in pbar:
score = 0
state, _ = env.reset()
done = False
states, actions, rewards, dones, next_states = [], [], [], [], []
while not done:
action = model.act(state)
next_state, reward, done, truncated,_ = env.step(action)
done = done or truncated
score += reward
states.append(state)
actions.append(action)
rewards.append(reward)
next_states.append(next_state)
dones.append(done)
state = next_state
states = torch.FloatTensor(np.array(states)).to(device)
actions = torch.LongTensor(np.array(actions)).view(-1, 1).to(device)
rewards = torch.FloatTensor(np.array(rewards)).view(-1, 1).to(device)
next_states = torch.FloatTensor(np.array(next_states)).to(device)
dones = torch.FloatTensor(np.array(dones)).view(-1, 1).to(device)
model.train(states, actions, rewards, next_states, dones)
scores.append(score)
pbar.set_postfix(ep=episode, score=score, avg100=np.mean(scores[-100:]))
if np.mean(scores[-100:]) > 200:
torch.save(model.actor.state_dict(),'../../model/cartpole-a.pt')
torch.save(model.critic.state_dict(),'../../model/cartpole-c.pt')
print(np.mean(scores[-100:]))
plt.plot(scores)
plt.show()完整程序
python
import gymnasium as gym, torch, torch.nn as nn, numpy as np, matplotlib.pyplot as plt
from collections import deque
env = gym.make("CartPole-v1", render_mode="human")
state_dim = env.observation_space.shape[0] if len(env.observation_space.shape) == 1 else env.observation_space.n
action_dim = env.action_space.n
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
class Actor(nn.Module):
def __init__(self, hidden_dim = 128):
super(Actor, self).__init__()
self.net = nn.Sequential(
nn.Linear(state_dim, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, action_dim), nn.Softmax(dim=-1)
)
def forward(self, x):
return self.net(x)
class Critic(nn.Module):
def __init__(self, hidden_dim = 128):
super(Critic, self).__init__()
self.net = nn.Sequential(
nn.Linear(state_dim, hidden_dim),nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),nn.ReLU(),
nn.Linear(hidden_dim, 1)
)
def forward(self, x):
return self.net(x)
class ActorCritic():
def __init__(self, gamma):
self.actor = Actor().to(device)
self.critic = Critic().to(device)
self.optimizer_a = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.optimizer_c = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
def act(self, states):
states = torch.from_numpy(states).float().to(device)
with torch.no_grad():
probs = self.actor(states)
disk = torch.distributions.Categorical(probs)
return disk.sample().item()
def train(self, states, actions, rewards, next_states, dones):
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones)
td_delta = td_target - self.critic(states)
log_probs = torch.log(self.actor(states).gather(1, actions) + 1e-9)
actor_loss = torch.mean(-log_probs * td_delta.detach())
critic_loss = nn.functional.mse_loss(self.critic(states), td_target.detach())
self.optimizer_c.zero_grad()
self.optimizer_a.zero_grad()
critic_loss.backward()
actor_loss.backward()
self.optimizer_c.step()
self.optimizer_a.step()
torch.manual_seed(0)
actor_lr = 1e-4
critic_lr = 1e-3
gamma = 0.99
scores = []
episodes = 1000
model = ActorCritic(gamma)
from tqdm import tqdm
pbar = tqdm(range(episodes), desc="Training")
for episode in pbar:
score = 0
state, _ = env.reset()
done = False
states, actions, rewards, dones, next_states = [], [], [], [], []
while not done:
action = model.act(state)
next_state, reward, done, truncated,_ = env.step(action)
done = done or truncated
score += reward
states.append(state)
actions.append(action)
rewards.append(reward)
next_states.append(next_state)
dones.append(done)
state = next_state
states = torch.FloatTensor(np.array(states)).to(device)
actions = torch.LongTensor(np.array(actions)).view(-1, 1).to(device)
rewards = torch.FloatTensor(np.array(rewards)).view(-1, 1).to(device)
next_states = torch.FloatTensor(np.array(next_states)).to(device)
dones = torch.FloatTensor(np.array(dones)).view(-1, 1).to(device)
model.train(states, actions, rewards, next_states, dones)
scores.append(score)
pbar.set_postfix(ep=episode, score=score, avg100=np.mean(scores[-100:]))
torch.save(model.actor.state_dict(),'../../model/cartpole-a.pt')
torch.save(model.critic.state_dict(),'../../model/cartpole-c.pt')
print(np.mean(scores[-100:]))
plt.plot(scores)
plt.show()模型测试
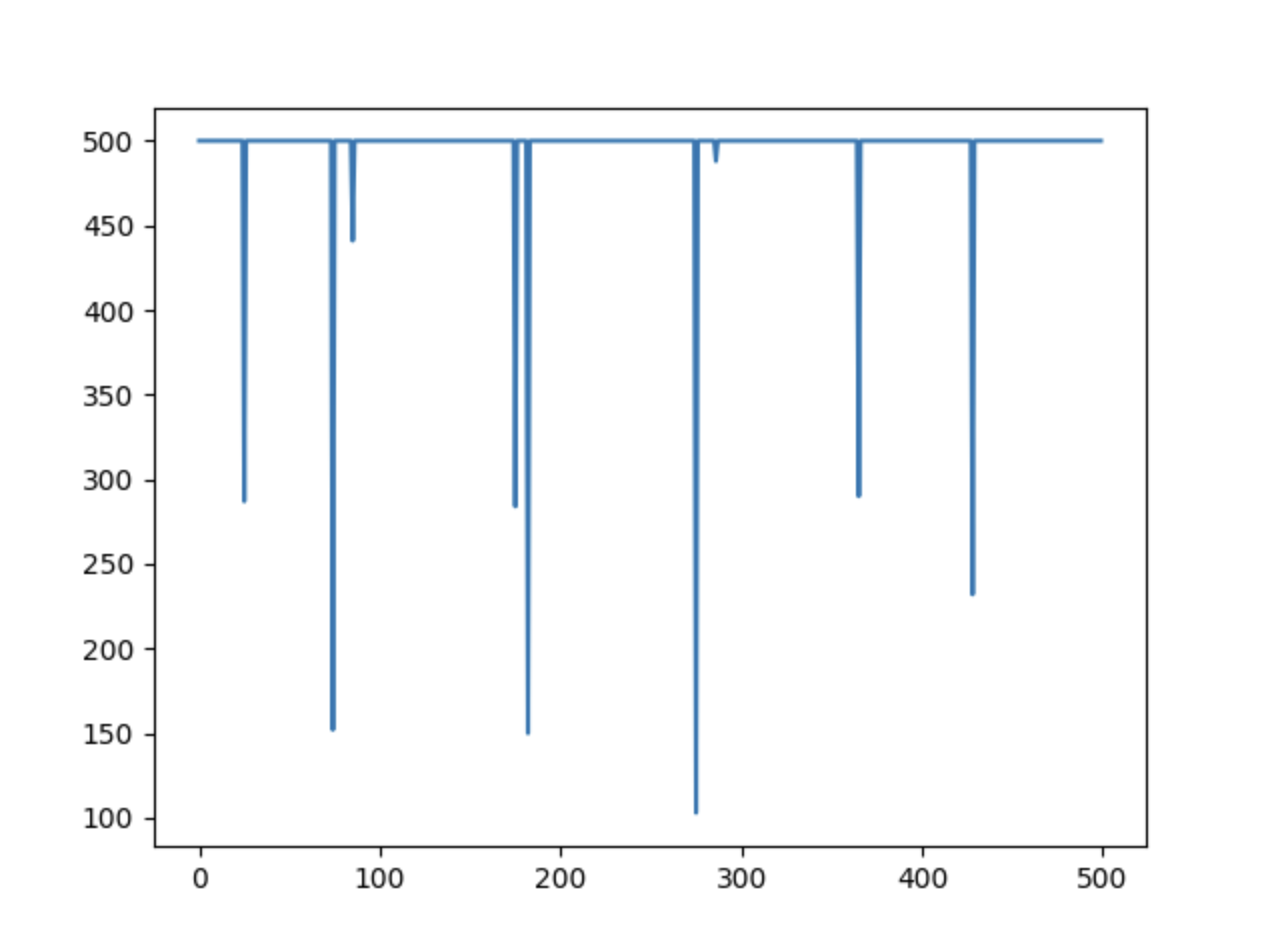
这里选择 500 500 500轮测试,结果如下:
模型绝大部分时间可以保证到游戏结束才停止,即少部分时间才会出现波动,而采取 D Q N DQN DQN时可能仅能达到平均 300 300 300到成绩