收发分离多基地雷达椭圆联合定位：原理、算法与误差分析

收发分离多基地雷达椭圆联合定位：原理、算法与误差分析

前言

多基地（multistatic）雷达由多组相互独立的发射机（Tx）与接收机（Rx）构成。对收发分离 的双基地量测而言，目标到某一对焦点（Tx、Rx）的距离和 为常数，其等值曲线为椭圆。将多组双基地椭圆进行联合定位，即可在平面（或空间）内估计目标位置。本文系统给出几何模型、量测方程、最小二乘/最大似然求解、误差传播与 Cramér--Rao 下界（CRLB），并讨论可观测性、鲁棒估计与工程实现要点。

正文

1. 几何模型与坐标系

在二维直角坐标系中记目标位置为 x=[x,y]⊤\mathbf{x}=[x,y]^\topx=[x,y]⊤，第 iii 组双基地的发射机与接收机位置分别为 Ti=[Tix,Tiy]⊤\mathbf{T}i=[T{ix},T_{iy}]^\topTi=[Tix,Tiy]⊤、Ri=[Rix,Riy]⊤\mathbf{R}i=[R{ix},R_{iy}]^\topRi=[Rix,Riy]⊤。

双基地几何距离和：
hi(x)≜∣x−Ti∣2+∣x−Ri∣2. h_i(\mathbf{x}) \triangleq |\mathbf{x}-\mathbf{T}_i|_2+|\mathbf{x}-\mathbf{R}_i|_2 . hi(x)≜∣x−Ti∣2+∣x−Ri∣2.

其中：
x\mathbf{x}x：目标二维位置向量；
Ti\mathbf{T}_iTi：第 iii 组发射机位置向量；
Ri\mathbf{R}_iRi：第 iii 组接收机位置向量；
∣⋅∣2|\cdot|_2∣⋅∣2：欧氏范数（欧氏距离）。

若第 iii 组的双程传播时延 为 τb,i\tau_{b,i}τb,i，则对应的距离和量测 为
rb,i=cτb,i, r_{b,i}=c\tau_{b,i}, rb,i=cτb,i,

其中：
rb,ir_{b,i}rb,i：第 iii 组的距离和（单位 m）；
ccc：电磁波在自由空间的传播速度（约 2.99792458×1082.99792458\times10^82.99792458×108 m/s）；
τb,i\tau_{b,i}τb,i：第 iii 组的双程时间量测（单位 s）。

忽略噪声时，椭圆等式为
Ei={x∈R2 | ∥x−Ti∥2+∥x−Ri∥2=rb,i}. \mathcal{E}_i=\left\{\mathbf{x}\in\mathbb{R}^2 \,\middle|\, \|\mathbf{x}-\mathbf{T}_i\|_2+\|\mathbf{x}-\mathbf{R}_i\|2=r{b,i}\right\}. Ei={x∈R2 ∥x−Ti∥2+∥x−Ri∥2=rb,i}.

其中：
Ei\mathcal{E}_iEi：第 iii 组双基地椭圆的点集；

其余符号同前。

对单条椭圆，若设半长轴 ai=rb,i2a_i=\tfrac{r_{b,i}}{2}ai=2rb,i、双焦距 2ci=∣Ti−Ri∣22c_i=|\mathbf{T}_i-\mathbf{R}_i|_22ci=∣Ti−Ri∣2，则半短轴
bi=ai2−ci2. b_i=\sqrt{a_i^2-c_i^2}. bi=ai2−ci2 .

其中：
aia_iai：第 iii 条椭圆的半长轴；
bib_ibi：第 iii 条椭圆的半短轴；
cic_ici：焦点到椭圆中心的距离；

其余符号同前。

注：要使椭圆存在，需 rb,i>∣Ti−Ri∣2r_{b,i}>|\mathbf{T}_i-\mathbf{R}_i|_2rb,i>∣Ti−Ri∣2。

2. 量测模型与统计假设

考虑 mmm 组双基地量测，加入高斯噪声：
zi=hi(x)+vi,vi∼N(0,σi2), z_i = h_i(\mathbf{x}) + v_i,\quad v_i\sim\mathcal{N}(0,\sigma_i^2), zi=hi(x)+vi,vi∼N(0,σi2),

其中：
ziz_izi：第 iii 组的实际观测（距离和，单位 m）；
hi(x)h_i(\mathbf{x})hi(x)：噪声自由的理论距离和；
viv_ivi：零均值高斯噪声；
σi2\sigma_i^2σi2：第 iii 组量测噪声方差；
N(⋅,⋅)\mathcal{N}(\cdot,\cdot)N(⋅,⋅)：高斯分布。

将各观测堆叠得
z=h(x)+v,v∼N(0,Σ), \mathbf{z}=\mathbf{h}(\mathbf{x})+\mathbf{v},\quad \mathbf{v}\sim\mathcal{N}(\mathbf{0},\mathbf{\Sigma}), z=h(x)+v,v∼N(0,Σ),

其中：
z=[z1,...,zm]⊤\mathbf{z}=[z_1,\ldots,z_m]^\topz=[z1,...,zm]⊤：观测向量；
h(x)=h1(x),...,hm(x)]⊤\mathbf{h}(\mathbf{x})=h_1(\mathbf{x}),\ldots,h_m(\mathbf{x})]^\toph(x)=h1(x),...,hm(x)]⊤：理论量测向量；
v\mathbf{v}v：噪声向量；
Σ=diag(σ12,...,σm2)\mathbf{\Sigma}=\mathrm{diag}(\sigma_1^2,\ldots,\sigma_m^2)Σ=diag(σ12,...,σm2)：噪声协方差矩阵。

3. 定位目标：最小二乘与最大似然

在高斯噪声下，最大似然等价于加权最小二乘：
x^=arg⁡min⁡xJ(x)≜12∣W1/2(h(x)−z)∣22, \widehat{\mathbf{x}}=\arg\min_{\mathbf{x}} J(\mathbf{x})\triangleq \tfrac{1}{2}\left|\mathbf{W}^{1/2}\big(\mathbf{h}(\mathbf{x})-\mathbf{z}\big)\right|_2^2, x =argxminJ(x)≜21 W1/2(h(x)−z) 22,

其中：
x^\widehat{\mathbf{x}}x ：位置估计；
J(x)J(\mathbf{x})J(x)：加权残差二范数目标函数；
W=Σ−1\mathbf{W}=\mathbf{\Sigma}^{-1}W=Σ−1：权矩阵（噪声协方差的逆）；
∣⋅∣2|\cdot|_2∣⋅∣2：二范数；
h(x)\mathbf{h}(\mathbf{x})h(x)、z\mathbf{z}z 同前。

4. 线性化与高斯--牛顿（GN）迭代

以当前迭代点 x(k)\mathbf{x}^{(k)}x(k) 进行一阶泰勒展开，定义残差
e(x)≜h(x)−z, \mathbf{e}(\mathbf{x}) \triangleq \mathbf{h}(\mathbf{x})-\mathbf{z}, e(x)≜h(x)−z,

其中：
e(x)\mathbf{e}(\mathbf{x})e(x)：残差向量；
h(x)\mathbf{h}(\mathbf{x})h(x)、z\mathbf{z}z 同前。

第 iii 个量测的雅可比行向量为
ji(x)=∂hi(x)∂x=x−Ti∣x−Ti∣2+x−Ri∣x−Ri∣2, \mathbf{j}_i(\mathbf{x})=\frac{\partial h_i(\mathbf{x})}{\partial \mathbf{x}} =\frac{\mathbf{x}-\mathbf{T}_i}{|\mathbf{x}-\mathbf{T}_i|_2}+\frac{\mathbf{x}-\mathbf{R}_i}{|\mathbf{x}-\mathbf{R}_i|_2}, ji(x)=∂x∂hi(x)=∣x−Ti∣2x−Ti+∣x−Ri∣2x−Ri,

其中：
ji(x)\mathbf{j}_i(\mathbf{x})ji(x)：第 iii 个量测对状态 x\mathbf{x}x 的梯度(1×2(1\times2(1×2 向量）；
∂hi/∂x\partial h_i/\partial \mathbf{x}∂hi/∂x：对 x\mathbf{x}x 的偏导；
Ti,Ri\mathbf{T}_i,\mathbf{R}_iTi,Ri、∣⋅∣2|\cdot|_2∣⋅∣2、x\mathbf{x}x 同前。

将所有 ji\mathbf{j}_iji 叠成雅可比矩阵
J(x)=[j1(x)⋮jm(x)], \mathbf{J}(\mathbf{x})= \begin{bmatrix} \mathbf{j}_1(\mathbf{x})\\ \vdots\\ \mathbf{j}_m(\mathbf{x}) \end{bmatrix}, J(x)= j1(x)⋮jm(x) ,

其中：
J(x)\mathbf{J}(\mathbf{x})J(x)：m×2m\times2m×2 的雅可比矩阵；
ji(x)\mathbf{j}_i(\mathbf{x})ji(x) 同前。

GN 更新：
Δx(k)=−(J⊤WJ)−1J⊤We(x(k)),x(k+1)=x(k)+Δx(k). \Delta\mathbf{x}^{(k)}= -\big(\mathbf{J}^\top\mathbf{W}\mathbf{J}\big)^{-1}\mathbf{J}^\top\mathbf{W}\mathbf{e}\big(\mathbf{x}^{(k)}\big),\quad \mathbf{x}^{(k+1)}=\mathbf{x}^{(k)}+\Delta\mathbf{x}^{(k)}. Δx(k)=−(J⊤WJ)−1J⊤We(x(k)),x(k+1)=x(k)+Δx(k).

其中：
Δx(k)\Delta\mathbf{x}^{(k)}Δx(k)：第 kkk 次迭代的增量；
J=J(x(k))\mathbf{J}=\mathbf{J}(\mathbf{x}^{(k)})J=J(x(k))：在 x(k)\mathbf{x}^{(k)}x(k)处的雅可比；
W\mathbf{W}W：权矩阵；
e(x(k))\mathbf{e}(\mathbf{x}^{(k)})e(x(k))：当前残差；
(⋅)−1(\cdot)^{-1}(⋅)−1：矩阵逆；
x(k+1)\mathbf{x}^{(k+1)}x(k+1)：更新后的估计。

为增强收敛性，可采用 LM 阻尼：
(J⊤WJ+λI)Δx=−J⊤We, \big(\mathbf{J}^\top\mathbf{W}\mathbf{J}+\lambda\mathbf{I}\big)\Delta\mathbf{x}=-\mathbf{J}^\top\mathbf{W}\mathbf{e}, (J⊤WJ+λI)Δx=−J⊤We,

其中：
λ>0\lambda>0λ>0：LM 阻尼因子；
I\mathbf{I}I：单位矩阵；

其余符号同前。

5. 可观测性与几何配置

本问题在二维中至少需要两条非退化椭圆 （即不同焦点构型、非同心同轴的测线）才能在几何上形成有限交点。局部可观测性可由信息矩阵的秩判断：
F(x)≜J⊤Σ−1J. \mathbf{F}(\mathbf{x})\triangleq \mathbf{J}^\top\mathbf{\Sigma}^{-1}\mathbf{J}. F(x)≜J⊤Σ−1J.

其中：
F(x)\mathbf{F}(\mathbf{x})F(x)：费舍尔信息矩阵（FIM）；
J\mathbf{J}J：雅可比矩阵；
Σ\mathbf{\Sigma}Σ：噪声协方差；
(⋅)⊤(\cdot)^\top(⋅)⊤：转置。

若 rank(F)=2\mathrm{rank}(\mathbf{F})=2rank(F)=2，则在该点局部可观测。几何精度指标可取
GDOP≜trace(F−1). \mathrm{GDOP}\triangleq \sqrt{\mathrm{trace}\big(\mathbf{F}^{-1}\big)}. GDOP≜trace(F−1) .

其中：
GDOP\mathrm{GDOP}GDOP：几何精度因子（值越小几何越好）；
trace(⋅)\mathrm{trace}(\cdot)trace(⋅)：矩阵迹；
F−1\mathbf{F}^{-1}F−1：信息矩阵的逆；

其余符号同前。

6. 估计误差与 Cramér--Rao 下界（CRLB）

GN/WLS 在正确线性化与小噪声条件下的协方差近似为
Cov(x^)≈(J⊤Σ−1J)−1. \mathrm{Cov}(\widehat{\mathbf{x}})\approx \big(\mathbf{J}^\top\mathbf{\Sigma}^{-1}\mathbf{J}\big)^{-1}. Cov(x )≈(J⊤Σ−1J)−1.

其中：
Cov(x^)\mathrm{Cov}(\widehat{\mathbf{x}})Cov(x )：位置估计的协方差矩阵；
J\mathbf{J}J、Σ\mathbf{\Sigma}Σ 同前。

在无偏估计条件下，CRLB 给出协方差的理论下界：
Cov(x^)⪰F−1,F=J⊤Σ−1J. \mathrm{Cov}(\widehat{\mathbf{x}})\succeq \mathbf{F}^{-1},\quad \mathbf{F}=\mathbf{J}^\top\mathbf{\Sigma}^{-1}\mathbf{J}. Cov(x )⪰F−1,F=J⊤Σ−1J.

其中：
⪰\succeq⪰：半正定序关系；
F\mathbf{F}F：FIM；

其余符号同前。

7. 未同步/偏差建模（时钟偏差或系统延迟）

若所有量测共享一个未知偏差 bbb（例如系统时延），量测模型写作
zi=hi(x)+b+vi. z_i = h_i(\mathbf{x}) + b + v_i. zi=hi(x)+b+vi.

其中：
bbb：全局加性偏差（单位 m）；

其余符号同前。

将状态扩展为 θ=[x,y,b]⊤\boldsymbol{\theta}=[x,y,b]^\topθ=[x,y,b]⊤，其雅可比为
Jθ=[j1(x)1⋮⋮jm(x)1]. \mathbf{J}_\theta= \begin{bmatrix} \mathbf{j}_1(\mathbf{x}) & 1\\ \vdots & \vdots\\ \mathbf{j}_m(\mathbf{x}) & 1 \end{bmatrix}. Jθ= j1(x)⋮jm(x)1⋮1 .

其中：
Jθ\mathbf{J}_\thetaJθ：对扩展状态的雅可比(m×3)(m\times3)(m×3)；
ji(x)\mathbf{j}_i(\mathbf{x})ji(x)：对 [x,y][x,y][x,y] 的梯度；

右侧列向量 "1" 表示对偏差 bbb 的偏导；

其余符号同前。

相应的 GN/LM 更新、FIM 与 CRLB 只需将 J\mathbf{J}J 替换为 Jθ\mathbf{J}_\thetaJθ 即可。

8. 鲁棒估计（抗粗大误差）

当存在外点（非高斯大误差）时，可用 MMM-估计改写目标：
x^=arg⁡min⁡x∑i=1mρ(ei(x)σi), \widehat{\mathbf{x}}=\arg\min_{\mathbf{x}} \sum_{i=1}^m \rho\left(\frac{e_i(\mathbf{x})}{\sigma_i}\right), x =argxmini=1∑mρ(σiei(x)),

其中：
ρ(⋅)\rho(\cdot)ρ(⋅)：鲁棒损失函数（如 Huber、Cauchy）；
ei(x)=hi(x)−zie_i(\mathbf{x})=h_i(\mathbf{x})-z_iei(x)=hi(x)−zi：第 iii 个残差；
σi\sigma_iσi：量测标准差；

其余符号同前。

采用迭代重加权最小二乘 （IRLS），权值更新为
wi=ψ(ti)ti,ti=eiσi, w_i=\frac{\psi(t_i)}{t_i},\quad t_i=\frac{e_i}{\sigma_i}, wi=tiψ(ti),ti=σiei,

其中：
wiw_iwi：第 iii 个量测的鲁棒权；
ψ(t)=ρ′(t)\psi(t)=\rho'(t)ψ(t)=ρ′(t)：影响函数；
tit_iti：标准化残差；
ei,σie_i,\sigma_iei,σi 同前。

9. 三维扩展与多目标情形

三维时令 x=[x,y,z]⊤\mathbf{x}=[x,y,z]^\topx=[x,y,z]⊤，其量测函数保持不变：
hi(x)=∣x−Ti∣2+∣x−Ri∣2. h_i(\mathbf{x}) = |\mathbf{x}-\mathbf{T}_i|_2+|\mathbf{x}-\mathbf{R}_i|_2 . hi(x)=∣x−Ti∣2+∣x−Ri∣2.

其中：
x\mathbf{x}x：三维目标位置；
Ti,Ri\mathbf{T}_i,\mathbf{R}_iTi,Ri：三维台站坐标；

其余符号同前。

雅可比行向量推广为
ji(x)=x−Ti∣x−Ti∣2+x−Ri∣x−Ri∣2∈R1×3. \mathbf{j}_i(\mathbf{x})=\frac{\mathbf{x}-\mathbf{T}_i}{|\mathbf{x}-\mathbf{T}_i|_2}+\frac{\mathbf{x}-\mathbf{R}_i}{|\mathbf{x}-\mathbf{R}_i|_2}\in\mathbb{R}^{1\times 3}. ji(x)=∣x−Ti∣2x−Ti+∣x−Ri∣2x−Ri∈R1×3.

其中：
ji(x)\mathbf{j}_i(\mathbf{x})ji(x)：三维梯度行向量；

其余符号同前。

多目标情形需结合数据关联（如最近邻、JPDA）或稀疏重构方法，量测模型在目标维上以联合似然建模，这里不再展开。

10. 数值实现要点与可视化

（1）初始化：

可用各双基地焦点中点的几何中心作初值
x(0)=1m∑i=1mTi+Ri2. \mathbf{x}^{(0)}=\frac{1}{m}\sum_{i=1}^m \frac{\mathbf{T}_i+\mathbf{R}_i}{2}. x(0)=m1i=1∑m2Ti+Ri.

其中：
x(0)\mathbf{x}^{(0)}x(0)：初始位置；
Ti,Ri,m\mathbf{T}_i,\mathbf{R}_i,mTi,Ri,m 同前。

（2）收敛判据：
∣Δx(k)∣2<ϵx或∣e(x(k))∣2<ϵe. |\Delta\mathbf{x}^{(k)}|_2<\epsilon_x\quad \text{或}\quad |\mathbf{e}(\mathbf{x}^{(k)})|_2<\epsilon_e. ∣Δx(k)∣2<ϵx或∣e(x(k))∣2<ϵe.

其中：
ϵx,ϵe\epsilon_x,\epsilon_eϵx,ϵe：步长与残差阈值；
Δx(k)\Delta\mathbf{x}^{(k)}Δx(k)、e(⋅)\mathbf{e}(\cdot)e(⋅) 同前。

（3）可视化：

每条双基地椭圆可绘制等值线
fi(x,y)=(x−Tix)2+(y−Tiy)2+(x−Rix)2+(y−Riy)2−zi=0, f_i(x,y)=\sqrt{(x-T_{ix})^2+(y-T_{iy})^2}+\sqrt{(x-R_{ix})^2+(y-R_{iy})^2}-z_i=0, fi(x,y)=(x−Tix)2+(y−Tiy)2 +(x−Rix)2+(y−Riy)2 −zi=0,

其中：
fi(x,y)f_i(x,y)fi(x,y)：第 iii 条椭圆的隐式函数；
(x,y)(x,y)(x,y)：平面网格坐标；
Tix,Tiy,Rix,Riy,ziT_{ix},T_{iy},R_{ix},R_{iy},z_iTix,Tiy,Rix,Riy,zi 同前。

（4）误差椭圆（1σ）：

若得到 Cov(x^)\mathrm{Cov}(\widehat{\mathbf{x}})Cov(x )，其特征分解
Cov(x^)=VDV⊤, \mathrm{Cov}(\widehat{\mathbf{x}})=\mathbf{V}\mathbf{D}\mathbf{V}^\top, Cov(x )=VDV⊤,

其中：
V\mathbf{V}V：特征向量矩阵（主轴方向）；
D=diag(λ1,λ2)\mathbf{D}=\mathrm{diag}(\lambda_1,\lambda_2)D=diag(λ1,λ2)：特征值（主轴方差）；
λ1,λ2\lambda_1,\lambda_2λ1,λ2：两主轴方差；
⊤\top⊤：转置。

则 1σ 椭圆半轴为 (λ1,λ2)(\sqrt{\lambda_1},\sqrt{\lambda_2})(λ1 ,λ2 )，方向由 V\mathbf{V}V 给出。

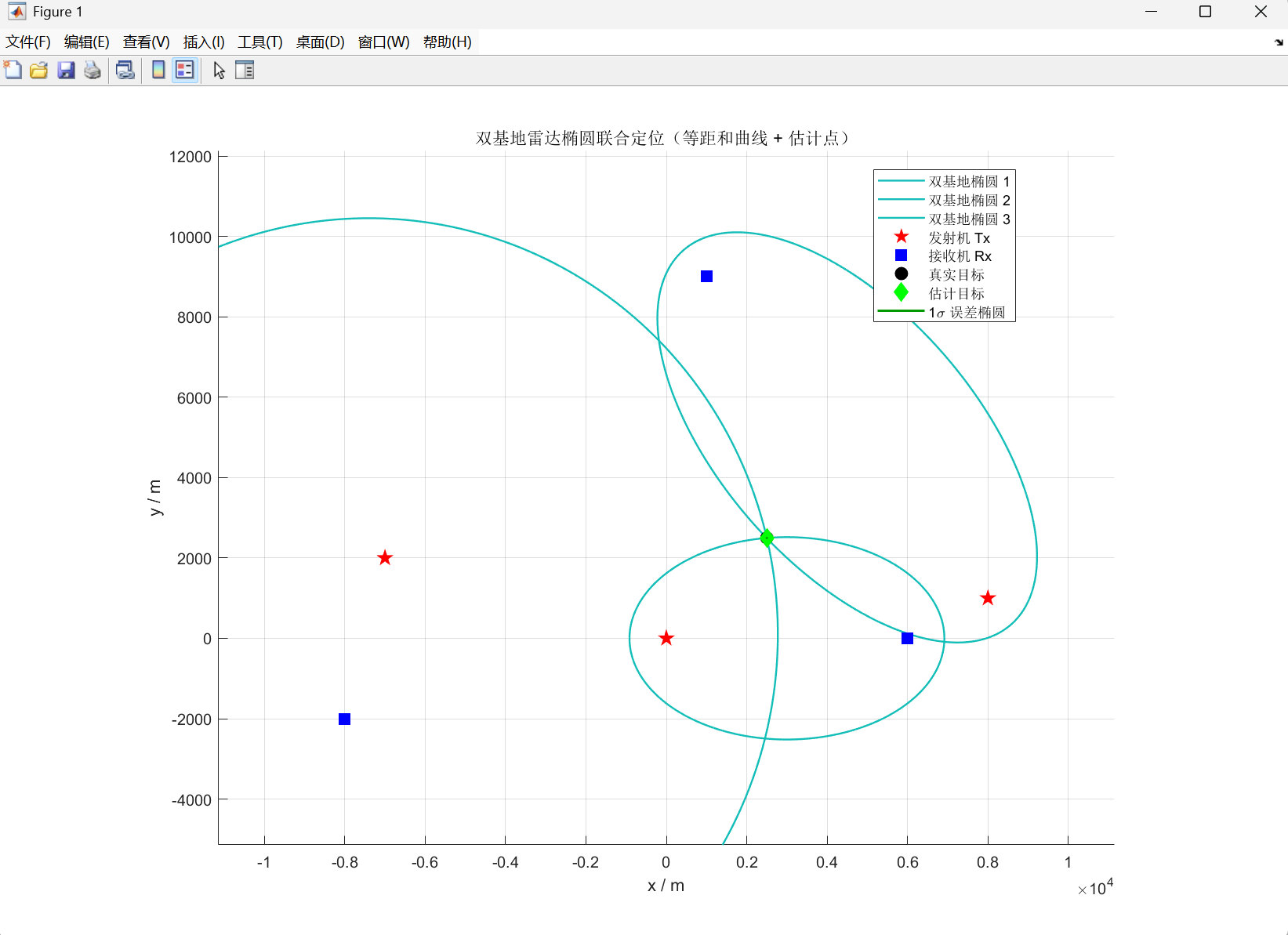
总结

本文从几何出发，建立了收发分离多基地雷达 的双基地距离和量测模型，证明单组量测对应椭圆约束，并在高斯噪声下将联合定位归结为加权最小二乘/最大似然 问题；随后给出基于雅可比的 GN/LM 迭代 、可观测性与几何指标、误差协方差与 CRLB 的闭式表达；进一步讨论了共享偏差建模 、鲁棒估计以及三维推广与可视化。工程实现中，合理的初值、阻尼调节与鲁棒权更新，可显著提升收敛性与抗外点能力；几何上应尽量拉大不同双基地基线的方向多样性，以降低 GDOP、改善定位精度。