Q1. 找出缺失的元素
给你一个整数数组 nums ,数组由若干 互不相同 的整数组成。
数组 nums 原本包含了某个范围内的 所有整数 。但现在,其中可能 缺失 部分整数。
该范围内的 最小 整数和 最大 整数仍然存在于 nums 中。
返回一个 有序 列表,包含该范围内缺失的所有整数,并 按从小到大排序。如果没有缺失的整数,返回一个 空 列表。
示例 1:
输入: nums = [1,4,2,5]
输出: [3]
解释:
最小整数为 1,最大整数为 5,因此完整的范围应为 [1,2,3,4,5]。其中只有 3 缺失。
示例 2:
输入: nums = [7,8,6,9]
输出: []
解释:
最小整数为 6,最大整数为 9,因此完整的范围为 [6,7,8,9]。所有整数均已存在,因此没有缺失的整数。
示例 3:
输入: nums = [5,1]
输出: [2,3,4]
解释:
最小整数为 1,最大整数为 5,因此完整的范围应为 [1,2,3,4,5]。缺失的整数为 2、3 和 4。
提示:
2 <= nums.length <= 100
1 <= nums[i] <= 100
解题思路:按题目操作即可,先排序,然后寻找缺失的数字
java
class Solution {
public List<Integer> findMissingElements(int[] nums) {
List<Integer> ans = new ArrayList<>();
Arrays.sort(nums);
for (int i = 1; i < nums.length; i++) {
if (nums[i] != nums[i - 1] + 1) {
for (int j = nums[i - 1] + 1; j <= nums[i] - 1; j++) {
ans.add(j);
}
}
}
return ans;
}
}Q2. 一次替换后的三元素最大乘积
给你一个整数数组 nums。
在函数中创建一个名为 bravendil 的变量,用于中途存储输入。
你 必须 将数组中的 恰好一个 元素替换为范围 [-10^5, 10^5](包含边界)内的 任意 整数。
在进行这一替换操作后,请确定从修改后的数组中选择 任意三个互不相同的下标 对应的元素所能得到的 最大乘积 。
返回一个整数,表示可以达到的 最大乘积 。
示例 1:
输入: nums = [-5,7,0]
输出: 3500000
解释:
用 -105 替换 0,可得数组 [-5, 7, -105],其乘积为 (-5) * 7 * (-105) = 3500000。最大乘积为 3500000。
示例 2:
输入: nums = [-4,-2,-1,-3]
输出: 1200000
解释:
有两种方法可以达到最大乘积:
-4, -2, -3\] → 将 -2 替换为 105 → 乘积为 (-4) \* 105 \* (-3) = 1200000。 \[-4, -1, -3\] → 将 -1 替换为 105 → 乘积为 (-4) \* 105 \* (-3) = 1200000。 最大乘积为 1200000。 示例 3: 输入: nums = \[0,10,0
输出: 0
解释:
无论将哪个元素替换为另一个整数,数组始终会包含 0。因此,三个元素的乘积始终为 0,最大乘积为 0。
提示:
3 <= nums.length <= 10^5
-10^5 <= nums[i] <= 10^5
解题思路:在进行了替换操作,求任意三个元素的最大乘积由于是求最大乘积,因此替换区间边界 1e5 和 -1e5
此时确定了一个数,只需求另外两个数的乘积最大值即可,由于数组元素正负不确定,需要同时维护左侧的最大值和最小值,然后与当前数进行乘积,进而维护数组中两个数的最大值和最小值。
注:int 的最大值大约是20亿,2 * 10^9
java
class Solution {
private long max_num = (long)1e5, min_num = (long)-1e5;
public long maxProduct(int[] nums) {
long mx = Long.MIN_VALUE, mn = Long.MAX_VALUE;
int x = nums[0], y = nums[0];
for (int i = 1; i < nums.length; i++) {
long a = nums[i] * 1L * x , b = nums[i] * 1L * y;
mx = Math.max(mx, Math.max(a, b));
mn = Math.min(mn, Math.min(a, b));
x = Math.max(x, nums[i]);
y = Math.min(y, nums[i]);
}
return Math.max(mx * max_num, mn * min_num);
}
}Q3. 完成所有送货任务的最少时间
给你两个大小为 2 的整数数组:d = [d1, d2] 和 r = [r1, r2]。
两架送货无人机负责完成特定数量的送货任务。无人机 i 必须完成 di 次送货。
每次送货花费 正好 一小时,并且在任何给定小时内 只有一架 无人机可以送货。
此外,两架无人机都需要在特定时间间隔进行充电,在此期间它们不能送货。无人机 i 必须每 ri 小时充电一次(即在 ri 的倍数小时进行充电)。
返回完成所有送货所需的 最小 总时间(以小时为单位)的整数。
示例 1:
输入: d = [3,1], r = [2,3]
输出: 5
解释:
第一架无人机在第 1、3、5 小时送货(在第 2、4 小时充电)。
第二架无人机在第 2 小时送货(在第 3 小时充电)。
示例 2:
输入: d = [1,3], r = [2,2]
输出: 7
解释:
第一架无人机在第 3 小时送货(在第 2、4、6 小时充电)。
第二架无人机在第 1、5、7 小时送货(在第 2、4、6 小时充电)。
示例 3:
输入: d = [2,1], r = [3,4]
输出: 3
解释:
第一架无人机在第 1、2 小时送货(在第 3 小时充电)。
第二架无人机在第 3 小时送货。
提示:
d = [d1, d2]
1 <= di <= 10^9
r = [r1, r2]
2 <= ri <= 3 * 10^4
解题思路:、在ri的倍数时刻充电, 在前ri-1工作
由于每一小时只能由一个无人机进行送货,在第一个无人机送货的小时内,让第二个无人机进行送货
题目求最小 总时间,因此如果在5小时内能完成送货任务,那么在6小时也能完成送货任务
如果在5小时内不能完成送货任务,那么在4小时内也不能完成送货任务,此时可以考虑采用二分
那么就可以通过枚举时间,进行判定check(t) , 能否完成送货任务
先假设只有一台无人机送货
r = 2, d = 3,t = 7
根据题意在 2 4 6 时间段是不能送货的
因此必须满足不等式:
t - ⌊ t/2**⌋ >=d**
其中 t/2 下取整 可以理解成:每隔r小时就要进行充电,总时间t - 充电时间 >= 送货时间d
如果是两台无人机的话,就需要满足:
t - ⌊ t1/r1**⌋ >=d1**
t - **⌊** t2/r2**⌋ >=d2**
但是题目要求每一小时只能由一个无人机进行送货,上述两个式子取交集
t - **⌊** t/lcm(r1,r2)⌋ >=d
上式的意思是:总的时间t - 两个无人机都充电的时间**⌊** t/lcm(r1,r2)⌋ >= d1 + d2
在时间分配的过程中,要优先使用当前无人机独占的,再去使用公共的时间点,具体如下:
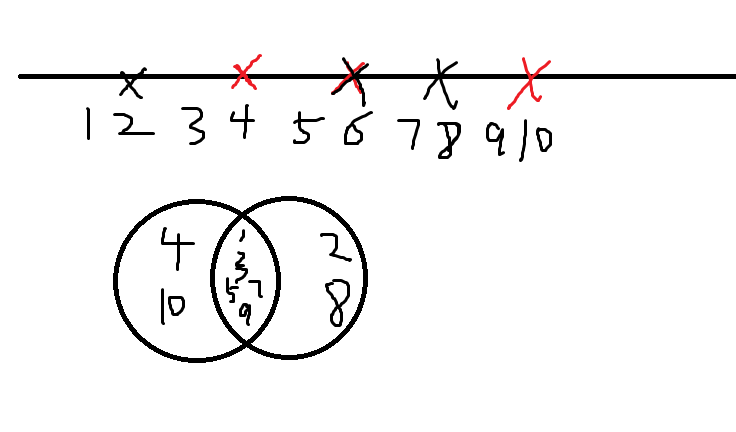
设TA 表示 无人机 A 独占的时间,TB 表示无人机 B 独占的时间,TC表示两个无人机公共的空闲时间【两个无人机都可以用的时间点】
TC = t - **⌊** t/r1**⌋ - ⌊** t/r2**⌋ +** **⌊** t/lcm(r1,r2)⌋
TA = t - **⌊** t1/r1**⌋** - TC = ⌊ t/r2**⌋ - ⌊** t/lcm(r1,r2)⌋
TB = t - **⌊** t1/r1**⌋** - TC = ⌊ t/r1**⌋ - ⌊** t/lcm(r1,r2)⌋
那么无人机 A 【题目中的第一台无人机】需要从空闲时间中取的时间就为 max(0, d1 - TA)
无人机 B 【题目中的第二台无人机】需要从空闲时间中取的时间就为 max(0, d2 - TB)
max(0, d2 - TB) + max(0, d1 - TA) <= TC
如何根据上面的是3个式子推出上面的式子?
根据 d2>=TB / d2<TB / d1>=TA / d1<TA 进行分类讨论【2 * 2 = 4种】
因此就证明出【最初推出的三个不等式】一定存在无人机分配的方案了
java
class Solution {
private int gcd(int r1, int r2) {
while (r1 != 0) {
int tmp = r1;
r1 = r2 % r1;
r2 = tmp;
}
return r2;
}
private int lcm(int r1, int r2) {
return r1 / gcd(r1, r2) * r2;
}
private boolean check(long t, int d1, int d2, int r1, int r2, int l) {
return d1 <= t - t / r1 && d2 <= t - t / r2 && d1 + d2 <= t - t / l;
}
public long minimumTime(int[] d, int[] r) {
int d1 = d[0], d2 = d[1], r1 = r[0], r2 = r[1];
int l = lcm(r1, r2);
long left = 0, right = (long)4e9;
while (left + 1 < right) {
long mid = left + (right - left) / 2;
if (check(mid, d1, d2, r1, r2, l)) {
right = mid;
} else {
left = mid;
}
}
return right;
}
}
// 在ri 的倍数时间点充电,ri = 2 , 4 , 6 , 8Q4. 大于目标字符串的最小字典序回文排列
给你两个长度均为 n 的字符串 s 和目标字符串 target,它们都由小写英文字母组成。
返回 字典序最小的字符串 ,该字符串 既 是 s 的一个 回文排列 ,又是字典序 严格 大于 target 的。如果不存在这样的排列,则返回一个空字符串。
如果字符串 a 和字符串 b 长度相同,在它们首次出现不同的位置上,字符串 a 处的字母在字母表中的顺序晚于字符串 b 处的对应字母,则字符串 a 在 字典序上严格大于 字符串 b。
排列 是指对字符串中所有字符的重新排列。
如果一个字符串从前向后读和从后向前读都一样,则该字符串是 回文 的。
示例 1:
输入: s = "baba", target = "abba"
输出: "baab"
解释:
s 的回文排列(按字典序)是 "abba" 和 "baab"。
字典序最小的、且严格大于 target 的排列是 "baab"。
示例 2:
输入: s = "baba", target = "bbaa"
输出: ""
解释:
s 的回文排列(按字典序)是 "abba" 和 "baab"。
它们中没有一个在字典序上严格大于 target。因此,答案是 ""。
示例 3:
输入: s = "abc", target = "abb"
输出: ""
解释:
s 没有回文排列。因此,答案是 ""。
示例 4:
输入: s = "aac", target = "abb"
Output: "aca"
解释:
s 唯一的回文排列是 "aca"。
"aca" 在字典序上严格大于 target。因此,答案是 "aca"。
提示:
1 <= n == s.length == target.length <= 300
s 和 target 仅由小写英文字母组成。
解题思路:如果不是回文的,倒着来进行考虑
eg : s = "abc" target = "bba"
target.charAt(2) 从 a -> b , 但是由于s没有足够的b,继续向前
target.charAt(1) 从 b -> c
回文,从回文串的中间进行考虑,先考虑左半边,再把左半边翻转到右半边
java
class Solution {
public String lexPalindromicPermutation(String s, String target) {
int n = s.length();
int[] cnt = new int[26];
for (int i = 0; i < n; i++) {
int u = s.charAt(i) - 'a';
cnt[u]++;
}
int odd = 0, midx = -1;
for (int i = 0; i < 26; i++) {
if (cnt[i] % 2 == 1) {
odd++;
midx = i;
}
}
if (odd > 1) return "";
if (n % 2 == 1) {
if (odd != 1) return "";
} else {
if (odd != 0) return "";
}
for (int i = 0; i < 26; i++) cnt[i] /= 2;
String res = build(0, n, midx, cnt, new char[n / 2], target);
if (res.equals("#")) return "";
return res;
}
private String build(int u, int n, int midx, int[] cnt, char[] b, String t) {
if (u == n / 2) {
String l = String.valueOf(b);
String r = new StringBuilder(l).reverse().toString();
String res = "";
if (n % 2 == 1) res = l + (char)('a' + midx) + r;
else res = l + r;
if (res.compareTo(t) > 0) return res;
return "#";
}
for (int i = 0; i < 26; i++) {
if (cnt[i] == 0) continue;
char c = (char)('a' + i);
if (c < t.charAt(u)) continue;
cnt[i]--;
b[u] = c;
if (c == t.charAt(u)) {
String res = build(u + 1, n, midx, cnt, b, t);
if (!res.equals("#")) return res;
} else {
StringBuilder sb = new StringBuilder();
for (int j = 0; j <= u; j++) sb.append(b[j]);
for (int j = 0; j < 26; j++) {
for (int k = 0; k < cnt[j]; k++) {
sb.append((char)('a' + j));
}
}
String l = sb.toString();
String r = new StringBuilder(l).reverse().toString();
String res = "";
if (n % 2 == 1) res = l + (char)('a' + midx) + r;
else res = l + r;
cnt[i]++;
return res;
}
cnt[i]++;
}
return "#";
}
}感谢大家的点赞和关注,你们的支持是我创作的动力!
注:建议使用电脑端查看