算法沉淀第七天（AtCoder Beginner Contest 428 和 小训练赛）

目录

引言：

[AtCoder Beginner Contest 428](#AtCoder Beginner Contest 428)

[Grandma's Footsteps](#Grandma's Footsteps)

题目分析

逻辑梳理

代码实现

[Most Frequent Substrings](#Most Frequent Substrings)

题目分析

逻辑梳理

代码实现

[Brackets Stack Query](#Brackets Stack Query)

题目分析

逻辑梳理

代码实现

小训练赛

货仓选址

题目分析

逻辑梳理

代码实现

[Epic Transformation](#Epic Transformation)

题目分析

逻辑梳理

代码实现

逆序对

题目分析

逻辑梳理

代码实现

结语：

---

引言：

今天是算法沉淀的第七天，今天我们依旧不寻找算法题来打，我们来讲解一下昨天打的AtCoder Beginner Contest 428 和 小小的一场训练赛

AtCoder Beginner Contest 428这个战绩如下，另一个训练赛就不放战绩了

因为 AtCoder Beginner Contest 428简单一点，所以我们先讲这场，再将小训练赛

那么，话不多说，我们就进入今天的算法讲解--------------------->

---

AtCoder Beginner Contest 428

Grandma's Footsteps

题目分析

题目链接在这A - Grandma's Footsteps

不想跳转的可看下图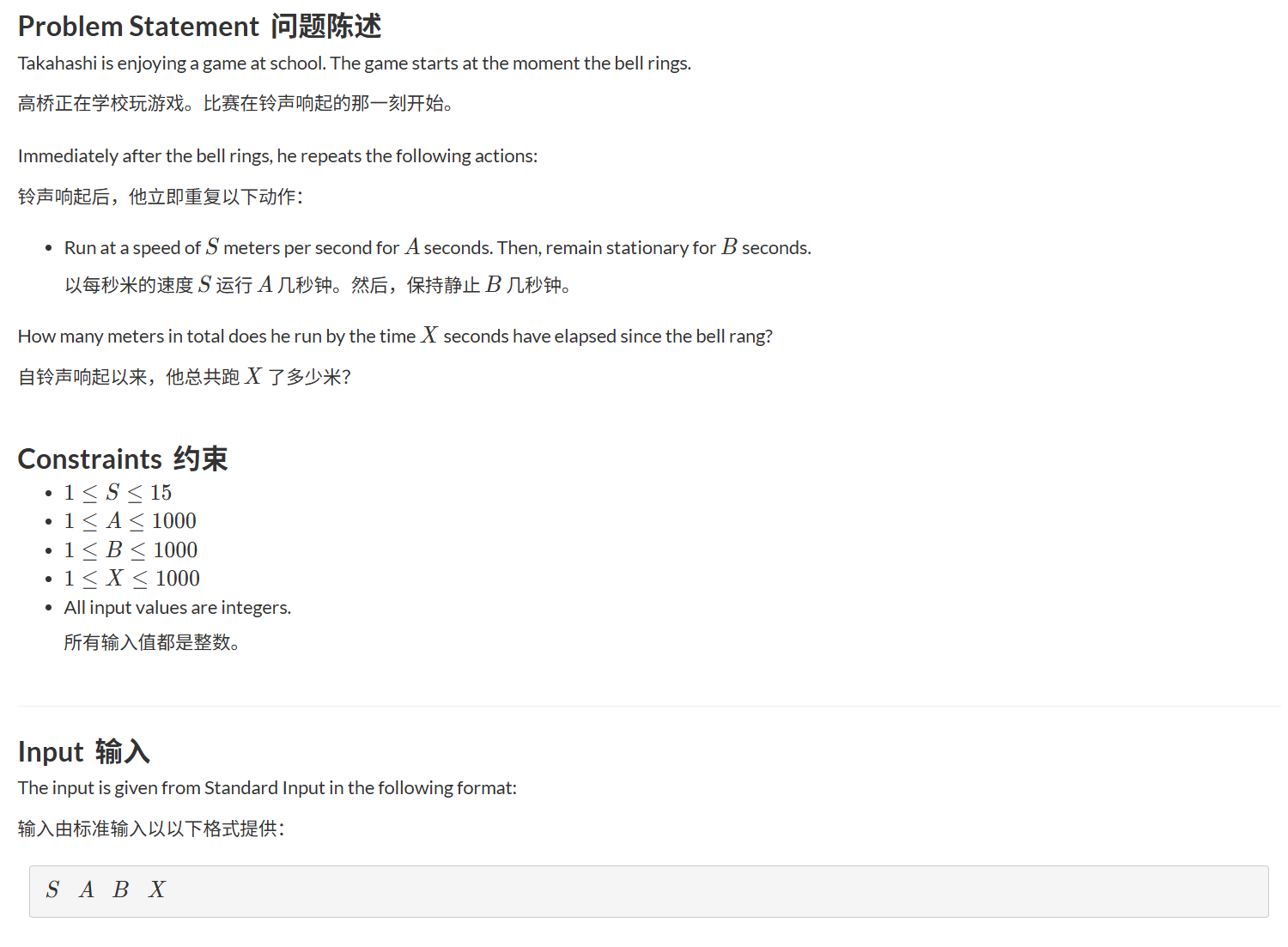

这题的题目意思很简单，就是给你四个数，S，A，B，X

S是速度，A是运动持续时间，B是休息时间，X是总时间

然后问你在这总时间内，能跑多远，输出值即可

---

逻辑梳理

这题就纯水题了，就算A+B这段时间内，他可以移动S*A的距离，然后每次跟移动完减去X就可以了，然后记得特判X小于A的时候这题就过了

---

代码实现

这里就直接放AC码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;

int t;

void solve()
{
	long long ans = 0;
	int s, a, b, x;
	cin >> s >> a >> b >> x;
	while (x>0)
	{
		if (x > a)
		{
			x -= a;
			ans += a * s;
		}
		else
		{
			ans += x * s;
			x = 0;
		}
		x -= b;
	}
	cout << ans << endl;
}

int main()
{
	
		solve();
	return 0;
}

---

Most Frequent Substrings

题目分析

这是题目链接B - Most Frequent Substrings

不想跳转的可看下图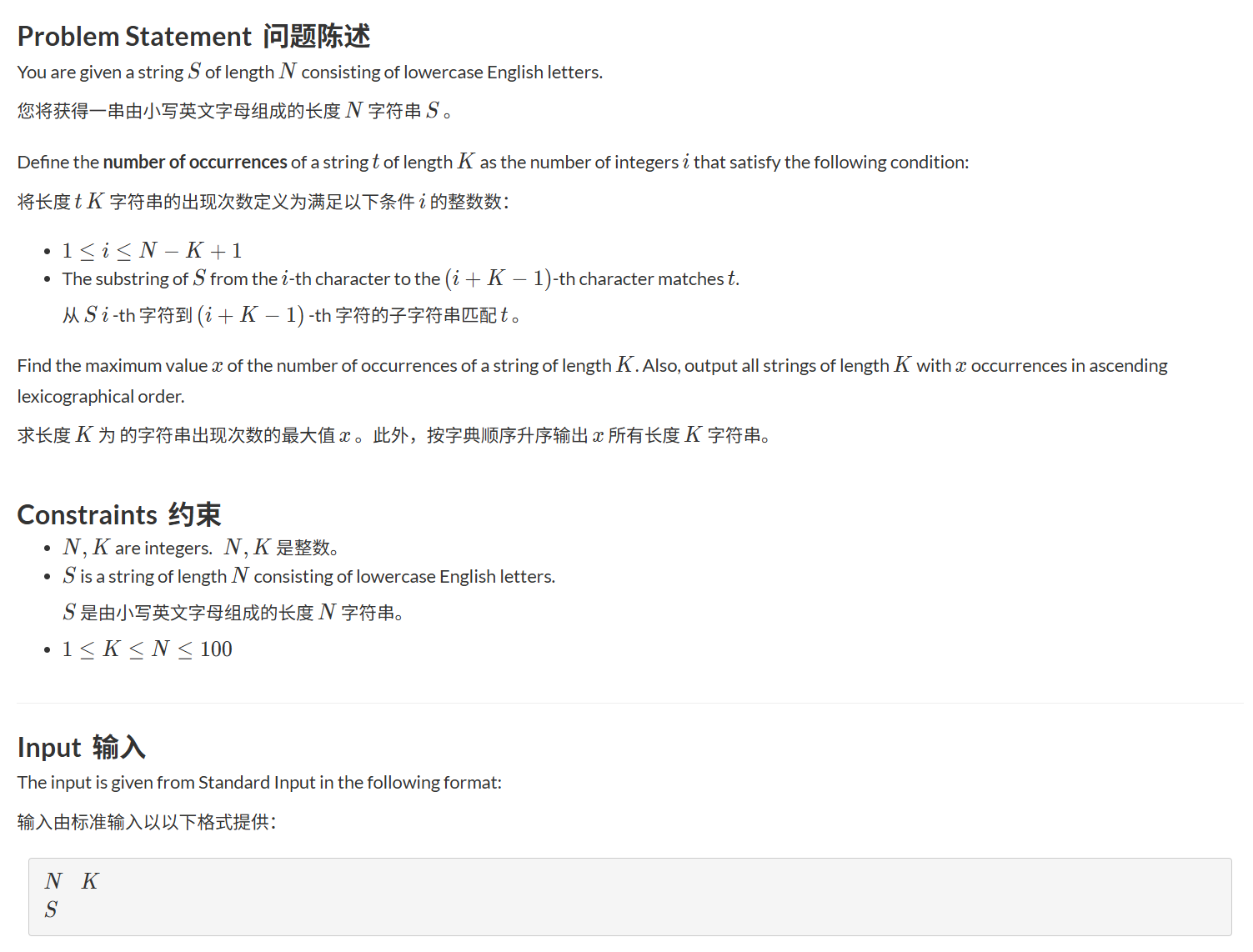

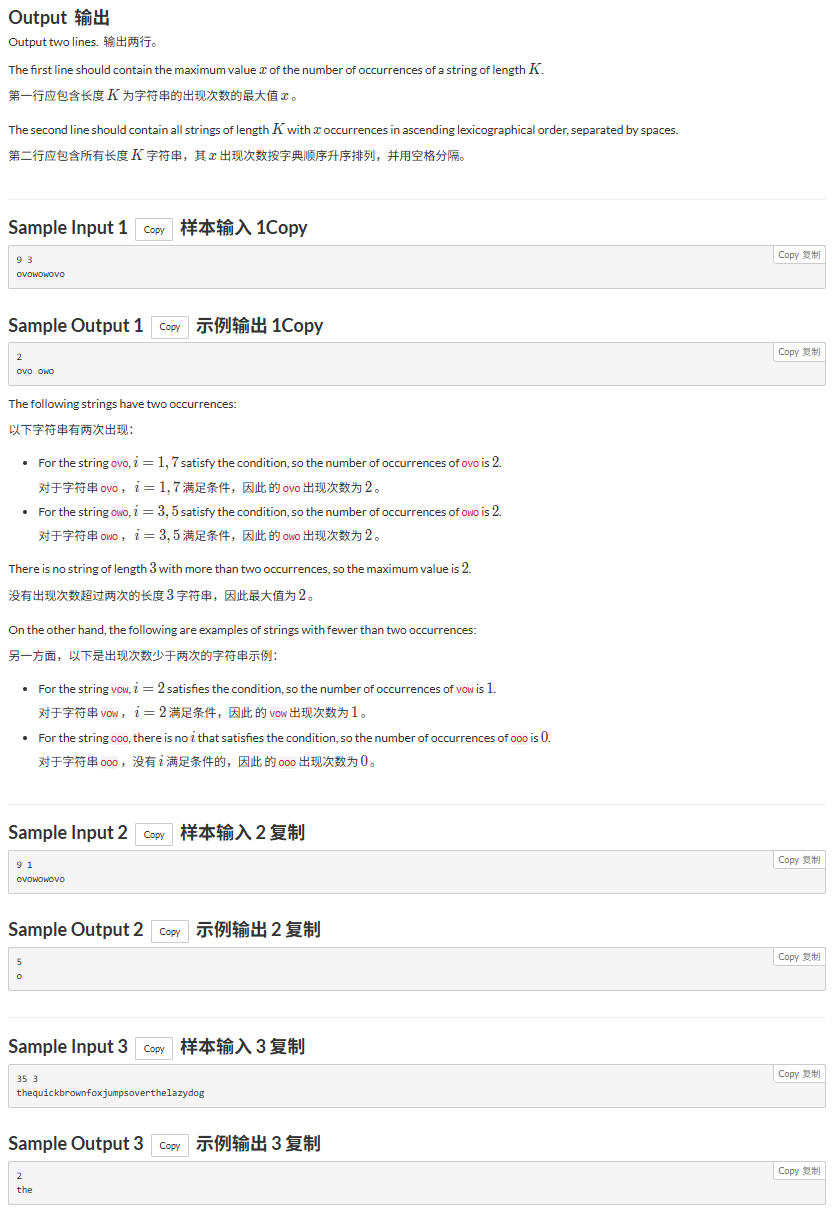
这题的题目意思也很简单，就是给你一个长度为N的字符串，然后问你在这个字符串中找出出现次数最多的长度为K的连续子串，然后输出次数是多少，接着再输出符合条件的子串（如果有多个就按照字典序从小到大排序）

这题意思就这么简单，那么接下来我们进入逻辑梳理环节

---

逻辑梳理

这题我们只需要开个结构体数组就可以了，然后结构体数组里面的元素存连续子串是什么，以及这个连续子串出现的次数就可以了

然后我们只需要把所有的连续子串找出来，然后每次找出连续字串后，判断这个子串不是不在结构体数组中已经出现过，如果出现过，就次数++，如果没出现过，就把这个子串放进结构体数组里，然后让次数变成1,

所有子串找完后，就直接对结构体数组进行排序就可以了，按照次数的出现次数排序，如果出现次数一样 ，就按字典序排序就可以了

然后最后先输出子串出现的最长次数

再输出符合条件的子串就可以了

那么逻辑梳理完了，接下来就进入代码实现环节

---

代码实现

这里就直接放AC码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;

int t;

struct node
{
	int ci;
	string a;
}ans[110];

bool cmp(node A, node B)
{
	if (A.ci == B.ci)
		return A.a < B.a;
	return A.ci > B.ci;
}

void solve()
{
	int wei = 0;
	int n, k;
	string s;
	cin >> n >> k;
	cin >> s;
	for (int i = 0; i < n - k + 1; i++)
	{
		char T[110] = "0";
		for (int j = i; j < i + k; j++)
		{
			T[j - i] = s[j];

		}
		int xixi = 1;
		for (int l = 0; l < wei; l++)
		{
			int xi = 1;
			for (int j = i; j < i + k; j++)
			{
				if (s[j] != ans[l].a[j - i])
				{
					xi = 0;
					break;
				}
			}
			if (xi)
			{
				ans[l].ci++;
				xixi = 0;
				break;
			}
		}
		if (xixi)
		{
			ans[wei].ci = 1;
			ans[wei++].a = T;
		}
	}
	sort(ans, ans + wei, cmp);
	cout << ans[0].ci << endl;
	for (int i = 0; i < wei; i++)
	{
		if (ans[i].ci != ans[0].ci)
			break;
		cout << ans[i].a << " ";
	}
	cout << endl;
}

int main()
{
	
		solve();
	return 0;
}

---

Brackets Stack Query

题目分析

这是题目链接C - Brackets Stack Query

不想跳转的可看下图

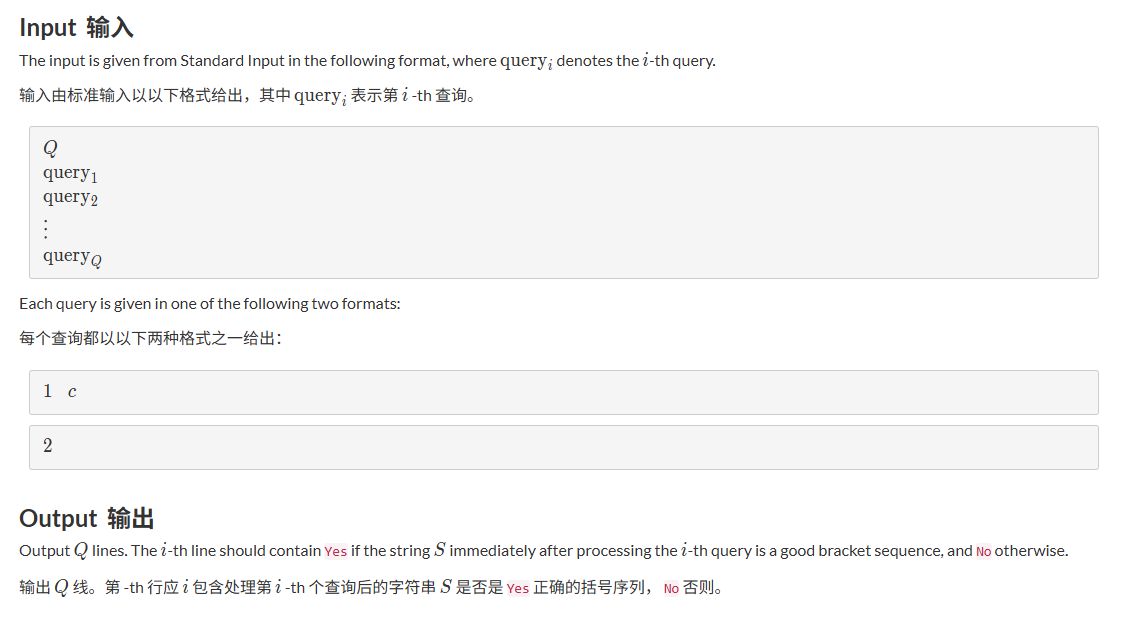
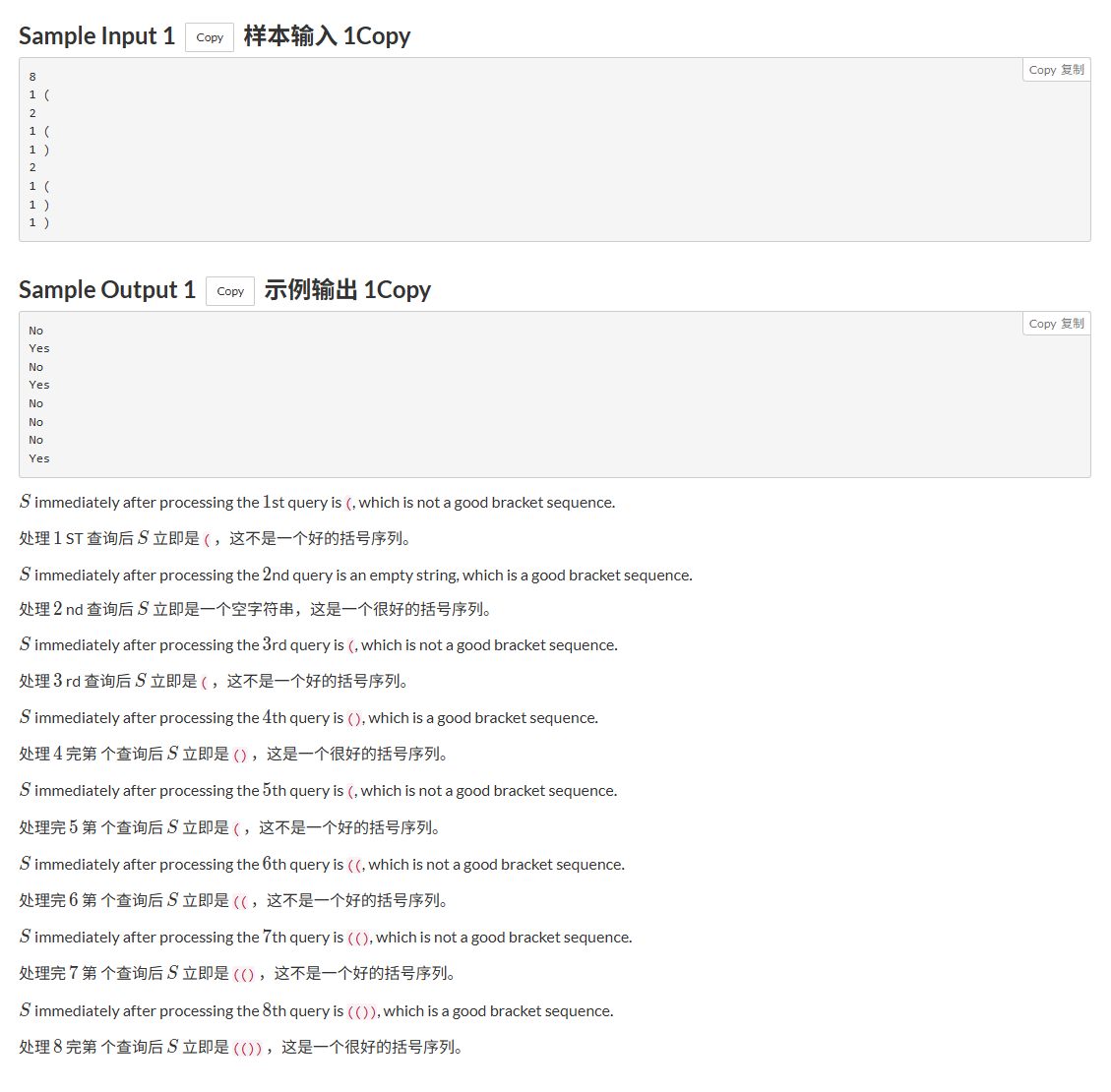
这题就是给你Q次操作，每次操作分为俩种

1. 1 c

c代表( 或 )，1的操作就是在队列末尾再放一个括号

2. 2

2就是把队列末的括号删掉

然后每次操作都要输出是YES还是NO

YES就是括号都是匹配的

NO就是括号不匹配

那么，这题题目就分析完啦，接下来，我们进入逻辑梳理环节

---

逻辑梳理

首先，最简单的，我们可以记录左括号和右括号的个数 ，然后，每次操作完后，我们对左括号和右括号的个数进行比较，如果一样多，就输出YES，反之则输出NO

那么，在这种情况下，大部分的情况都是能过的，但是也有特殊情况

因为括号肯定要左括号和右括号配对，尽管左右括号的个数一样多，但如果右括号出现时，左括号没有能与之配对，那就依旧输出NO

所以我们可以用一个数组，来存在哪一个地方会使得右括号比左括号多，如果右括号比左括号多了，不管后面怎么操作，都是NO，所以标记完这个位置后，直到把这个位置的括号删掉后，才可以接着判断YES或者NO

那么这题的逻辑梳理就梳理完啦，接下来，我们进入代码实现环节

---

代码实现

这里就直接放代码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;

int t;
char a[800010];
int r = 0;
int l = 0;
int wei = 1;
int pan = 0;
void solve()
{
	int c;
	cin >> c;
	if (c == 1)
	{
		cin >> a[wei];
		if (a[wei] == '(')
			l++;
		else
			r++;
		wei++;
		if (r > l && pan == 0)
			pan = wei;

	}
	else
	{
		if (a[--wei] == '(')
			l--;
		else
			r--;
		if (wei + 1 == pan)
			pan = 0;
	}
	if (l == r)
	{
		if (pan != 0)
			cout << "No" << endl;
		else
			cout << "Yes" << endl;
	}
	else
		cout << "No" << endl;
}

int main()
{
	cin >> t;
	while (t--)
		solve();
	return 0;
}

那么这场比赛的题就讲完啦，接下来我们来看小训练赛的题

---

小训练赛

这场就直接放题目图啦

货仓选址

题目分析

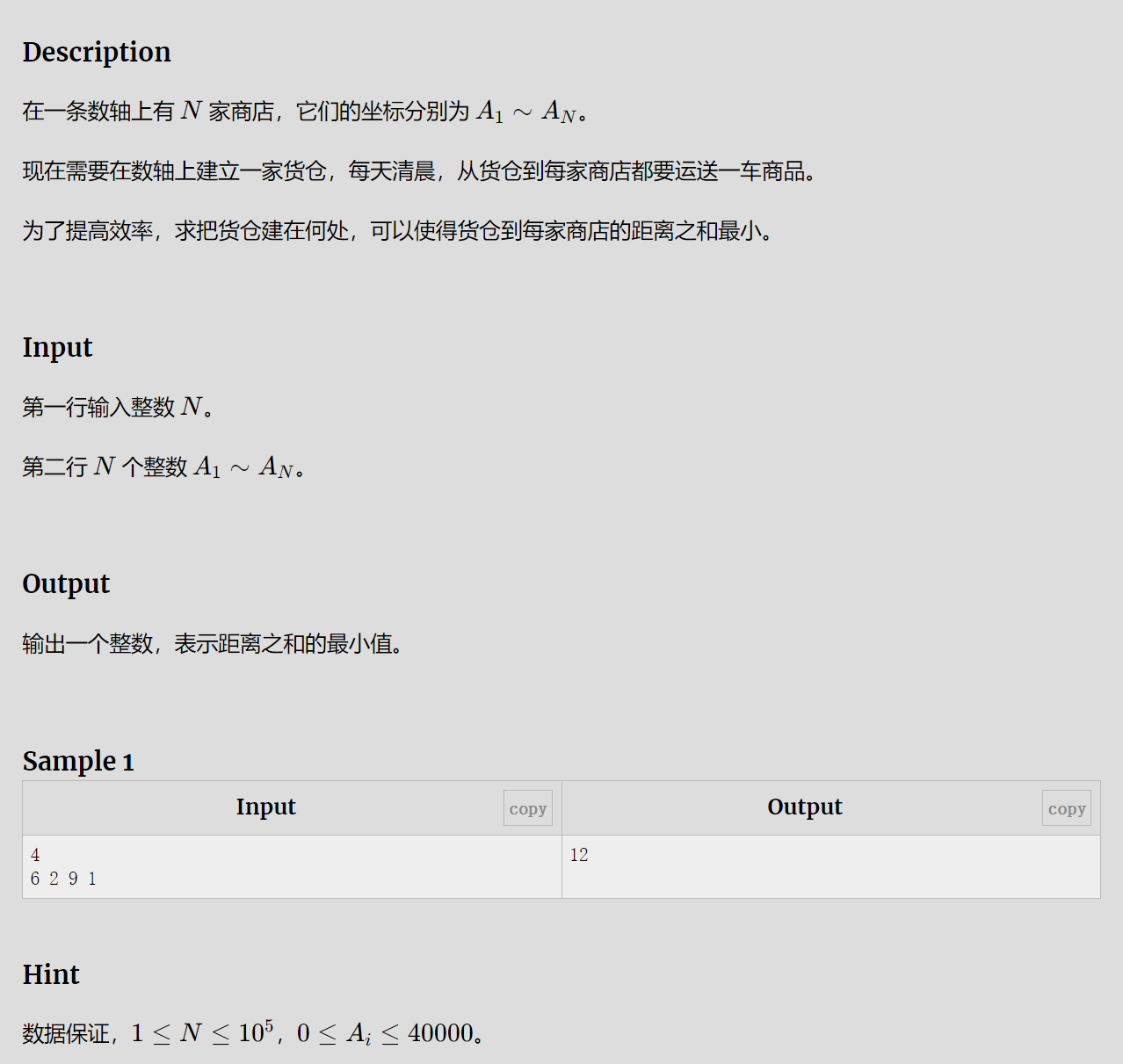
这题的题目意思很简单，就是给你几个商店的位置，每个位置相当于是在x轴的位置

然后题目让你在x轴上选一个位置作为仓库，然后这个点和所有商店的距离加起来要最小

输出加起来最小的那个值就可以啦

那么，题目就分析完啦，接下来我们进入逻辑梳理环节

---

逻辑梳理

这题因为要选位置，那乱序的数肯定不好选，所以，我们首先把这些数排序完，再进行操作

那么接下来我们来讨论商店的个数，假设商店个数为ｎ

如果商店的个数是奇数，我们把仓库的位置选在第（ｎ＋１）／２个商店的位置就是和最小的时候

如果商店的个数是偶数，我们把仓库的位置选在第ｎ／２和第ｎ／２＋１个商店位置之间的位置就是和最小的时候

那么，逻辑梳理完啦，接下来就进入代码实现环节

---

代码实现

这里就直接放AC码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;

int n;
int a[100010];

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
	sort(a + 1, a + n + 1);
	long long ans = 0;
	for (int i = 1; i <= n / 2; i++)
	{
		ans += a[n - i + 1] - a[i];
	}
	cout << ans << endl;
	return 0;
}

---

Epic Transformation

题目分析

这题的意思就是给你一个数组，然后每次都可以删掉２个不同的数，直到不能删为止，然后问最少可以剩下几个元素

这题题目意思就这么简单，接下来我们进入逻辑梳理环节

---

逻辑梳理

这题我们可以先找出出现最多次的元素的次数

１.如果出现次数最多的元素次数＞＝剩余元素个数

那就输出这个元素的个数－剩余元素个数

２.如果出现次数最多的元素次数＜剩余元素个数

２.１　如果是奇数情况，就输出１

２.２　如果是偶数情况，就输出０

那么，这题的逻辑就梳理完啦，接下来就进入代码实现环节

---

代码实现

这里就直接放代码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;

int t;
long long a[200010];

void solve()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	sort(a + 1, a + n + 1);
	int zui = 1;
	int k = 1;
	for (int i = 2; i <= n; i++)
	{
		if (a[i] == a[i - 1])
			k++;
		else
		{
			zui = max(zui, k);
			k = 1;
		}
	}
	zui = max(zui, k);
	if (n % 2)
	{
		if (zui > n - zui)
			cout << n - (n - zui) - (n - zui) << endl;
		else
			cout << "1" << endl;
	}
	else
	{
		if (zui > n - zui)
			cout << n - (n - zui) - (n - zui) << endl;
		else
			cout << "0" << endl;
	}
	return;
}

int main()
{
	cin >> t;
	while (t--)
	{
		solve();
	}
	return 0;
}

---

逆序对

题目分析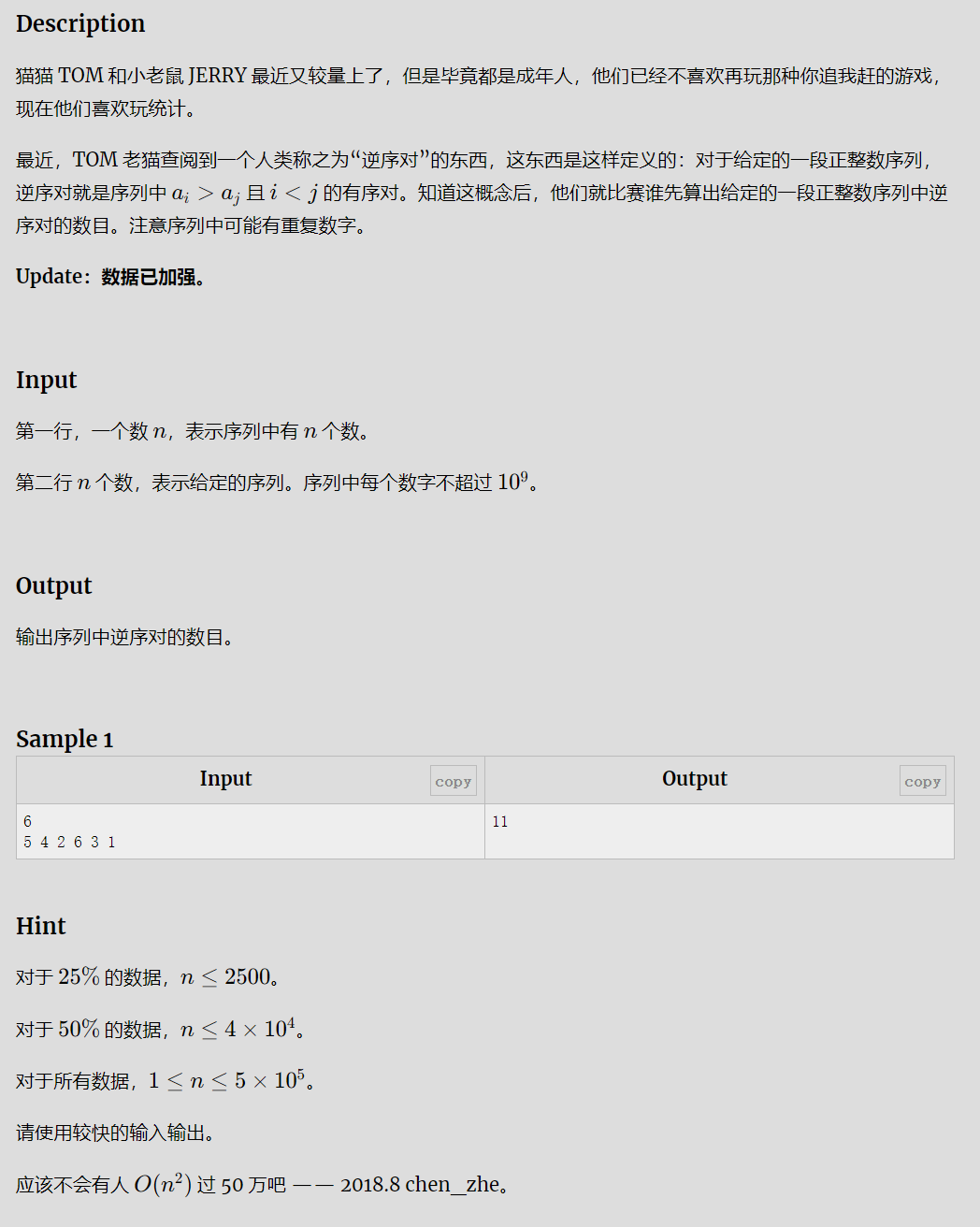

这题的要求也很简单，给你一个长度为ｎ的数组，让你找出这个数组中有几对逆序对，输出就好了

那么，接下来就进入逻辑梳理环节

---

逻辑梳理

这题直接暴力肯定是行不通的，那么我们可以想想有什么算法是可以找逆序对的呢？

对，就是归并排序，归并排序中，有这么一串核心代码

while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			b[j++] = a[begin1++];
		}
		else
		{
			ans += mid - begin1 + 1;
			b[j++] = a[begin2++];
		}
	}

这是看哪个小放那个，那么，当ａ［ｂｅｇｉｎ１］＞ａ［ｂｅｇｉｎ２］时，从ｂｅｇｉｎ１开始的前面那部分都可以和ａ［ｂｅｇｉｎ２］的元素组成逆序对，所以只需要在ｅｌｓｅ语句中加上迭代的表达式就可以了

归并排序完成之时，就是逆序对个数求出之时

那么这题的逻辑梳理就梳理完啦，接下来进入代码实现环节

---

代码实现

这里就直接放代码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;

long long ans = 0;
long long a[500010];
long long b[500010];

void guibing(int left, int right)
{
	if (left >= right)
		return;
	int mid = (left + right) / 2;
	int begin1 = left;
	int begin2 = mid + 1;
	int end1 = mid;
	int end2 = right;
	int j = 0;
	guibing(left, mid);
	guibing(mid + 1, right);
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			b[j++] = a[begin1++];
		}
		else
		{
			ans += mid - begin1 + 1;
			b[j++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
		b[j++] = a[begin1++];
	while (begin2 <= end2)
		b[j++] = a[begin2++];
	for (int i = left; i <= right; i++)
		a[i] = b[i - left];
}

void solve()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	guibing(1, n);
	cout << ans << endl;
}

int main()
{
	solve();
	return 0;
}

---

结语：

今日算法讲解到此结束啦，希望对你们有所帮助，谢谢观看，如果觉得不错可以分享给朋友哟。有什么看不懂的可以评论问哦，