第三章线型神经网络

3.1 线性回归

3.1.1线性回归的基本元素

自变量称为特征

每一行数据称为一个样本

调参是选择超参数的过程，通过验证数据集上的结果评估

损失函数

学习率

批量大小

泛化

关键要素是训练数据、损失函数、优化算法还有模型本身

3.1.2矢量化加速

为避免for循环的巨大内存开销，我们需要对数据进行矢量化，使其能够同时处理整个小批量的样本

矢量化使数学表达更加简洁，运行更快

3.1.3正态分布与平方损失

正态分布概率密度函数

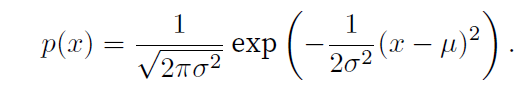
线性回归模型一般使用均方误差损失函数

3.1.4从线性回归到深度网络

输入数称为特征维度

线性回归，每个输入都与每个输出相连，我们称为全连接层

3.2 线性回归的从零实现

跳过

3.3 线性回归的简洁实现

3.3.1生成数据集

d2l库（Dive into Deep Learning）是《动手学深度学习》这本书的配套Python库。这本书是由李沐等人编写的著名深度学习教材，d2l库提供了书中使用的各种工具函数、数据集加载器、可视化工具等。

python 复制代码

import torch
from d2l import torch as d2l
true_w=torch.tensor([2,-3.4])
true_b=4.2
features,labels=d2l.synthetic_data(true_w,true_b,1000)

这段代码的目的是生成一个线性回归的人工数据集，该数据集的特征和标签关系由给定的权重和偏置决定，并带有一些随机噪声，1000个样本

3.3.2读取数据集

python 复制代码

from torch.utils import data
def load_array(data_arrays,batch_size,is_train=True):
    dataset=data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset=dataset,batch_size=batch_size,shuffle=is_train)
batch_size=10
data_iter=load_array((features,labels),batch_size)

3.3.3定义模型

Sequential类将多个层串联在一起

python 复制代码

from torch import nn
net=nn.Sequential(nn.Linear(2,1))

3.3.4初始化模型参数

指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样，偏置参数将初始化为零

python 复制代码

net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)

3.3.5定义损失函数

L2范数，均方误差函数

python 复制代码

loss=nn.MSELoss()

3.3.6定义优化算法

小批量随机梯度下降算法

python 复制代码

trainer=torch.optim.SGD(net.parameters(),lr=0.03)

3.3.7训练

data_iter 是一个数据迭代器 ，每次提供一个小批量的数据，在整个数据集（features, labels）上计算损失

python 复制代码

num_epochs=20
for epoch in range(num_epochs):
    for x,y in data_iter:
        l=loss(net(x),y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l=loss(net(features),labels)
    print(f"epoch{epoch+1},loss {l}")

python 复制代码

epoch1,loss 0.000263899564743042
epoch2,loss 0.00010184535494772717
epoch3,loss 0.00010029190889326856
epoch4,loss 9.984541247831658e-05
epoch5,loss 9.985241922549903e-05
epoch6,loss 9.982789924833924e-05
epoch7,loss 9.984560165321454e-05
epoch8,loss 0.00010191267938353121
epoch9,loss 0.00010141638631466776
epoch10,loss 9.986544318962842e-05
epoch11,loss 9.981977927964181e-05
epoch12,loss 0.00010064811795018613
epoch13,loss 0.00010026074596680701
epoch14,loss 9.997553570428863e-05
epoch15,loss 0.0001005627927952446
epoch16,loss 0.00010081498476210982
epoch17,loss 0.00010039070184575394
epoch18,loss 0.00010035681043518707
epoch19,loss 9.994090942200273e-05
epoch20,loss 9.985292854253203e-05

得到训练后的参数

python 复制代码

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

python 复制代码

w的估计误差： tensor([-4.9829e-05,  2.7299e-04])
b的估计误差： tensor([-7.6294e-06])

PyTorch中，data模块提供了数据处理工具，nn模块定义了大量的神经网络层和常见损失函数。

3.4 softmax回归

softmax回归适用于分类问题，它使用了softmax运算中输出类别的概率分布。

3.4.1分类问题

独热编码（one‐hot encoding）。独热编码是一个向量，它的分量和类别一样多。类别对

应的分量设置为1，其他所有分量设置为0。

3.4.2网络架构

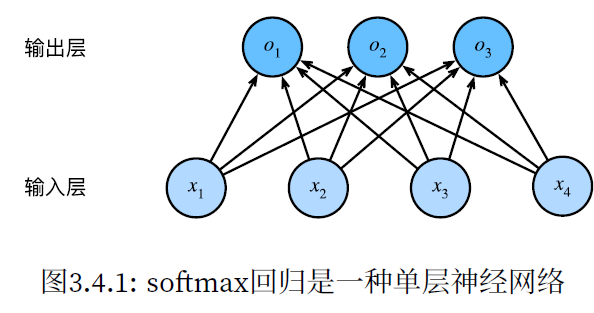
3.4.4softmax运算

softmax运算获取一个向量并将其映射为概率，确保输出非负且各输出之和为1，可以表示概率

3.4.6交叉熵损失函数

交叉熵是一个衡量两个概率分布之间差异的很好的度量，它测量给定模型编码数据所需的比特数

3.5 图像分类数据集

3.5.1读取数据集

Fashion‐MNIST是一个服装分类数据集，由10个类别的图像组成，每个类别由训练数据集（train dataset）中的6000张图像和测试数据集（test dataset）中的1000张图像组成

每个输入图像的高度和宽度均为28像素。数据集由灰度图像组成，其通道数为1

python 复制代码

from torchvision import transforms
import torchvision
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../data", train=False, transform=trans, download=True)

3.5.2读取小批量

数据迭代器是获得更高性能的关键组件

num_workers=4 表示使用4个独立的子进程来并行加载和预处理数据

4个子进程同时从磁盘读取不同的数据批次，每个进程独立进行数据预处理

python 复制代码

batch_size = 256
def get_dataloader_workers(): #@save
"""使用4个进程来读取数据"""
return 4
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers())

3.5.3整合所有组件

.insert(index,element)函数将Resize函数插入到开头，需要先调整大小，再转换为张量， 顺序不能颠倒

python 复制代码

def load_data_fashion_mnist(batch_size, resize=None): #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                num_workers=get_dataloader_workers()))

3.6 softmax回归的从零开始实现

3.6.1初始化模型参数

样本数据集中每个样本为28*28的图像，像素个数为784，输出与类别相同10个类别

python 复制代码

import torch
num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

3.6.2定义softmax操作

python 复制代码

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition # 这里应用了广播机制

3.6.3定义模型

因为w为784*10，进行.mamtul(）矩阵乘法时，x要为（-1,784）大小，所以要先reshape

python 复制代码

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

3.6.4定义损失函数

对于单标签分类的交叉熵损失函数，y_hat为预测值的概率分布，y为真实标签索引

python 复制代码

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

cross_entropy(y_hat, y)

第三章 线型神经网络

3.1 线性回归

3.1.1线性回归的基本元素

3.1.2矢量化加速

3.1.3正态分布与平方损失

3.1.4从线性回归到深度网络

3.2 线性回归的从零实现

3.3 线性回归的简洁实现

3.3.1生成数据集

3.3.2读取数据集

3.3.3定义模型

3.3.4初始化模型参数

3.3.5定义损失函数

3.3.6定义优化算法

3.3.7训练

3.4 softmax回归

3.4.1分类问题

3.4.2网络架构

3.4.4softmax运算

3.4.6交叉熵损失函数

3.5 图像分类数据集

3.5.1读取数据集

3.5.2读取小批量

3.5.3整合所有组件

3.6 softmax回归的从零开始实现

3.6.1初始化模型参数

3.6.2定义softmax操作

3.6.3定义模型

3.6.4定义损失函数

第三章线型神经网络