数据结构——二十六、邻接表(王道408)

文章目录

• 前言
• 一.存储结构(顺序+链式存储)
• • 1.思路
  • 2.代码表示
  • 3.存储无向图
  • 4.存储有向图
• 二.求无向图指定节点的度
• 三.求有向图指定节点的入度,出度和度
• 四.图的邻接表表示方法不唯一
• 五.知识回顾与重要考点
• 结语

前言

本文介绍了图的邻接表存储结构及其应用。邻接表采用链式存储方式，通过顶点数组和边链表实现图的表示。文章详细讲解了无向图和有向图的存储方法，分析了空间复杂度，并阐述了如何计算节点的度数。对于有向图，重点讨论了入度和出度的求解方法。同时指出邻接表表示方式不唯一的特性，与邻接矩阵的唯一性形成对比。最后总结了重要考点，包括邻接表的优缺点、适用场景以及时间复杂度分析。

一.存储结构(顺序+链式存储)

1.思路

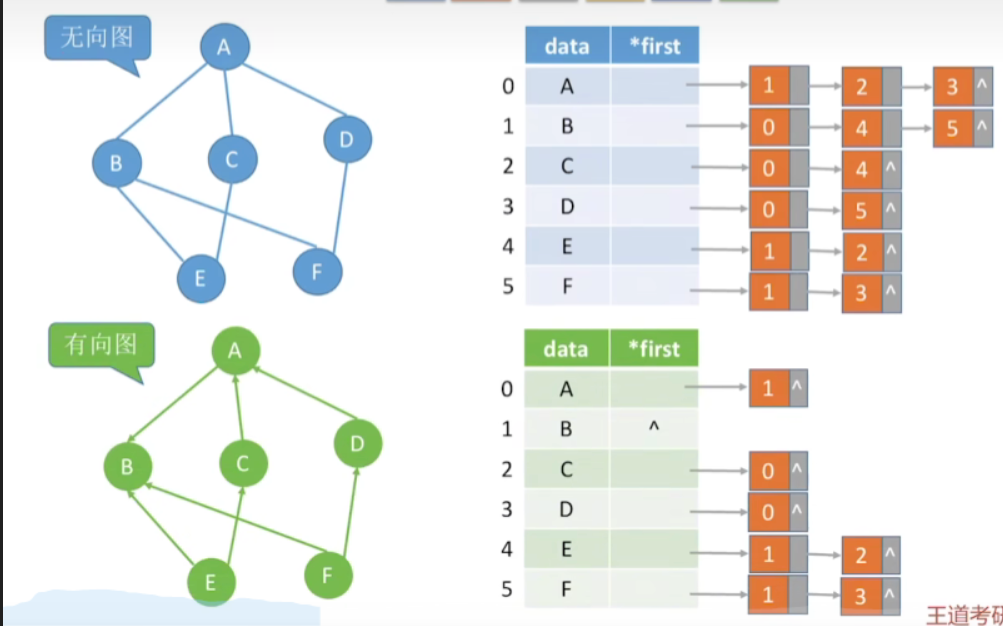
• 和之前树的孩子兄弟表示法思路差不多,先存储图的各个顶点与第一条边作为一个链表的头结点,然后链表再存入每个顶点对应的其他边和其他边所连接的顶点

2.代码表示

//"顶点"
typedef struct VNode{
	VertexType data;//顶点信息
	ArcNode*first;//第一条边/弧
}VNode,AdjList[MaxVertexNum];

//用邻接表存储的图
typedef struct{
	AdjList vertices;//顶点结点的数组
	int vexnum,arcnum;//记录具体有多少个结点,多少条边
} ALGraph;

//"边/弧"
typedef struct ArcNode{
int adjvex;//边/弧指向哪个结点
struct ArcNode *next;//指向下一条弧的指针
//InfoType info;        //边权值(可选)
}ArcNode;

3.存储无向图

• 边结点的数量是2|E|，整体空间复杂度为O(|V|+2|E|)

4.存储有向图

• 边结点的数量是|E|，整体空间复杂度为O(|V|+|E|)

二.求无向图指定节点的度

• 我们只需要便利和这个顶点相关的这个边链表,有多少个边节点它的度就是多少

• 遍历这个边链表可以找到和当前的这个顶点相连的所有的边

三.求有向图指定节点的入度,出度和度

• 有向图的度等于入度加上出度

• 如果要找到一个节点的出度,我们只需要遍历和这个节点相关的这个边节点的链表,这个链表反映的是从当前节点出去的这些弧

• 如果要找入度还有指向当前节点的弧,这就比较麻烦了

• 比如我们要统计A节点的入度或者说要找到指向A的弧,那唯一的办法就是把所有的这些节点的边链表都依次的遍历一遍

这也是用连接表这种方式存储有向图的一个一个比较大的缺点

四.图的邻接表表示方法不唯一

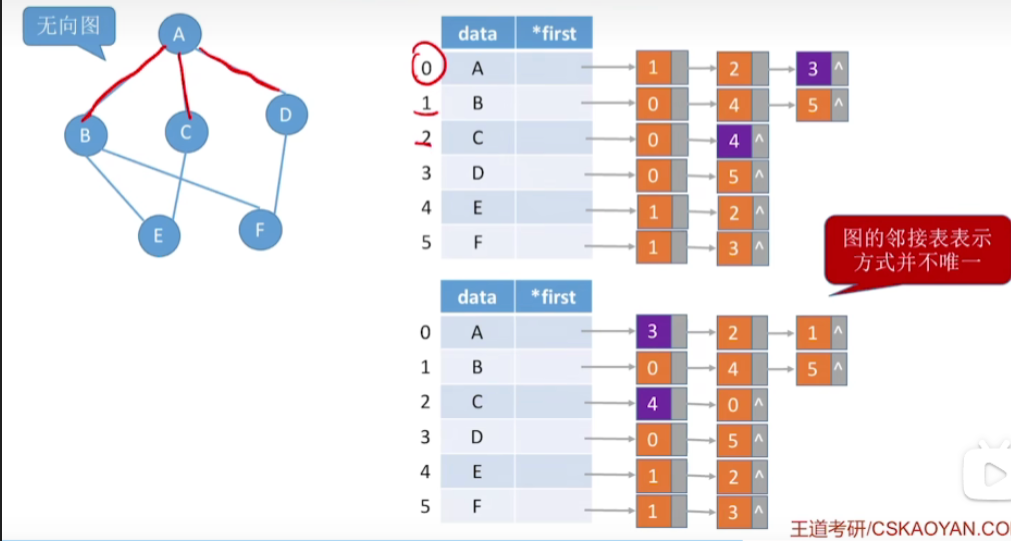
• 图的邻接表表示方式并不唯一,比如说A这个节点和BCD都相连
• 那A节点的边列表其实可以用BCD这样的顺序,当然也可以用DCB这样的顺序
• 也就是说各个边在这个列表当中出现的先后顺序是任意的

只要确定了顶点编号，图的邻接矩阵表示方式唯一,这和我们这一节学习的邻接表法有很大区别

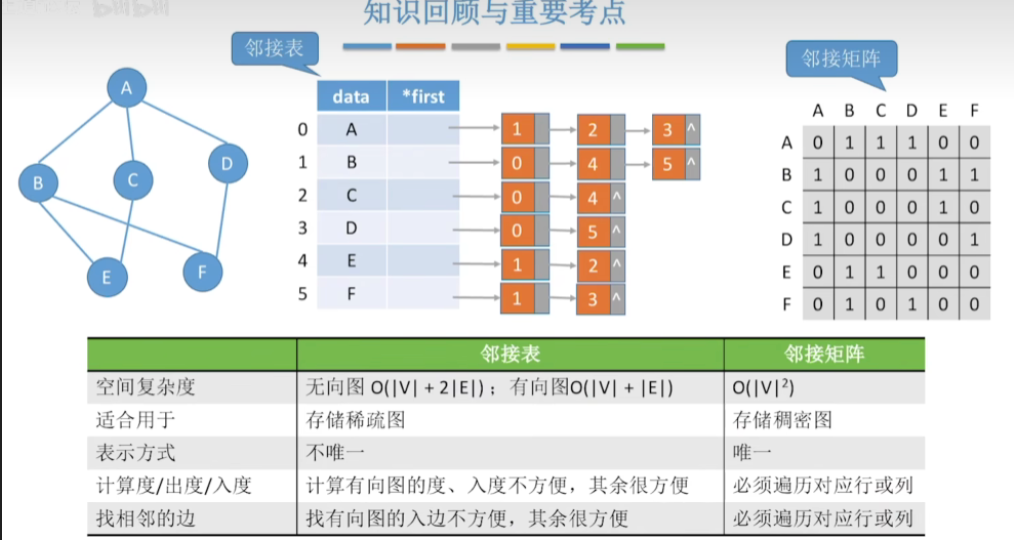
五.知识回顾与重要考点

结语

二更😉,这一节王道只讲了这么点,可不是我偷懒😖
如果想查看更多章节,请点击:一、数据结构专栏导航页