Python机器学习---1.数据类型和算法：线性回归

**数据类型：**如需分析数据，了解我们要处理的数据类型非常重要。我们可以将数据类型分为三种主要类别：

**数值（Numerical）：**数据是数字，可以分为两种数值类别:
1. 离散数据（Discrete Data）限制为整数的数字。例如:经过的汽车数量。
2. 连续数据（Continuous Data）具有无限值的数字。例如:一件商品的价格或一件商品的大小。
**分类（Categorical）：**是无法相互度量的值。例如:颜色值或任何 yes/no 值。
**序数（Ordinal）：**类似于分类数据，但可以相互度量。示例:A 优于 B 的学校成绩，依此类推。

**回归：**当我们尝试找到变量之间的关系时，会用到术语"回归"（regression）。在机器学习和统计建模中，这种关系用于预测未来事件的结果。

**线性回归：**线性回归是⼀种⽤于建模和分析两个变量之间关系的统计⽅法。在线性回归中，我们假设两个变量之间存在线性关系，即⼀个变量的值可以通过另⼀个变量的线性组合来预测。线性回归的基本原理是通过找到⼀条最佳拟合直线（或超平⾯，对于多维情况）来表示两个变量之间的关系。简单来说线性回归使用数据点之间的关系在所有数据点之间画一条直线。这条线可以用来预测未来的值。

**拟合：**是指构建⼀种算法(数学函数)，使得该算法能够符合真实的数据。从机器学习⻆度讲，线性回归就是要构建⼀个线性函数，使得该函数与⽬标值之间的相符性最好。从空间的⻆度来看，就是要让函数的直线（⾯)，尽可能靠近空间中所有的数据点（点到直线的平⾏于y轴的距离之和最短)。线性回归会输出⼀个连续值。

下面这条直线被称为回归线，⽤来最⼩化实际观测值与线性模型预测值之间的差异。这个差异通常⽤残差（实际值与预测值之间的差异）的平⽅和来度量，这就是所谓的最⼩⼆乘法。

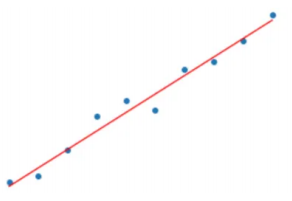
**线性回归模型：**y如果连续值我们成为回归算法，y是离散值我们称为分类算法。

简单线性回归：ŷ = w*x+b

python 复制代码

# 生成测试数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)

# 线性回归实例
modeL = LinearRegression()

# 划分数据集：训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, random_state=0)

# 拟合
modeL.fit(X_train, y_train)
slope = modeL.coef_    # 权重（斜率）
intercept = modeL.intercept_    # 截距

# 预测
Y = modeL.predict(X_test)

# 可视化
plt.figure(figsize=(12, 8))
plt.rcParams['font.family']='SimHei'
plt.plot(y_test,label='真实值',color='red',marker='o')
plt.plot(Y,label='预测值',color='yellow',marker='D')
plt.xlabel('预测集序号')
plt.ylabel('数据值')
plt.legend()
plt.show()

# 模型评估
# print("均方误差：",mean_squared_error(y_test,Y))
# print("平均绝对误差：",mean_absolute_error(y_test,Y))
# print("训练集:",r2_score(y_train,modeL.predict(X_train)))
# print("测试集:",r2_score(y_test,Y))

多元线性回归：ŷ = w1*x1+w2*x2+w3*x3+.....wn*xn+b

python 复制代码

# 导入数据
df = pd.read_csv(f'boston_housing_data.csv')    # 波斯顿房价数据集

# 处理空值
df['MEDV'] = df['MEDV'].fillna(0)

# 指定特征列和目标列
X = df.drop(columns='MEDV')     # 特征列
y = df['MEDV']      #目标列

# 线性回归实例
lmode = LinearRegression()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, random_state=1)

# 拟合
lmode.fit(X_train, y_train)

# 预测
Y = lmode.predict(X_test)

# 可视化
plt.figure(figsize=(12, 8))
plt.rcParams['font.family'] = 'Microsoft YaHei'
plt.scatter(range(len(y_test)), y_test, label='真实值', color='red', marker='o')
plt.scatter(range(len(Y)), Y, label='预测值', color='yellow', marker='D')
plt.xlabel('预测集序号')
plt.ylabel('数据值')
plt.legend()
plt.show()

# 模型评估
# print("均方误差：",mean_squared_error(y_test,Y))
# print("平均绝对误差：",mean_absolute_error(y_test,Y))
# print("训练集:",r2_score(y_train,lmode.predict(X_train)))
# print("测试集:",r2_score(y_test,Y))

**模型评估：**回归模型评估，当我们建⽴好模型后，模型的效果如何呢?对于回归模型，我们可以采⽤如下的指标来进⾏衡量。在上面的Python代码内我也写了相应模型评估方法。

MSE均⽅误差：MSE (Mean Squared Error)，平均平⽅误差，为所有样本数据误差（真实值与预测值之差)的平⽅和，然后取均值。均⽅误差是指参数估计值与参数真值之差平⽅的期望值；MSE可以评价数据的变化程度，MSE的值越⼩，说明预测模型描述实验数据具有更好的精确度。
RMSE均⽅根误差：RMSE (Root Mean Squared Error)，平均平⽅误差的平⽅根，即在MSE的基础上，取平⽅根。
MAE平均绝对值误差：MAE(Mean Absolute Error)，平均绝对值误差，为所有样本数据误差的绝对值和。平均绝对误差能更好地反映预测值误差的实际情况。
R^2分数：R^2为决定系数，⽤来表示模型拟合性的分值，值越⾼表示模型拟合性越好，在训练集中，R^2的取值范围为[0,1]。在测试集（未知数据)中，R^2的取值范围为[-∞,1]。R^2的计算公式为1减去RSS与TSS的商。其中，TSS(Total Sum of Squares)为所有样本数据与均值的差异，是⽅差的m倍。⽽RSS(Residual sum of squares)为所有样本数据误差的平⽅和，是MSE的m倍。