你知道一维空间的二次方程是什么样子的吗?比如ax² + bx + c,x²项使它成为二次方程。
二次型是x²项的多维版本。在二维空间中,它看起来像:
ax² + bxy + cy²
注意,每个项的次数都是 2: (x², xy, y²)。没有像 x 或 y 这样的线性项,也没有常数项。
美妙之处在于:v^T H v 恰好是一个二次型。将其相乘,得到:
v₁²·(∂²f/∂x²) + 2v₁v₂·(∂²f/∂x∂y) + v₂²·(∂²f/∂y²)
每个项的 v 分量的次数都是 2。Hessian 矩阵只是所有这些二次系数的一种简洁写法。
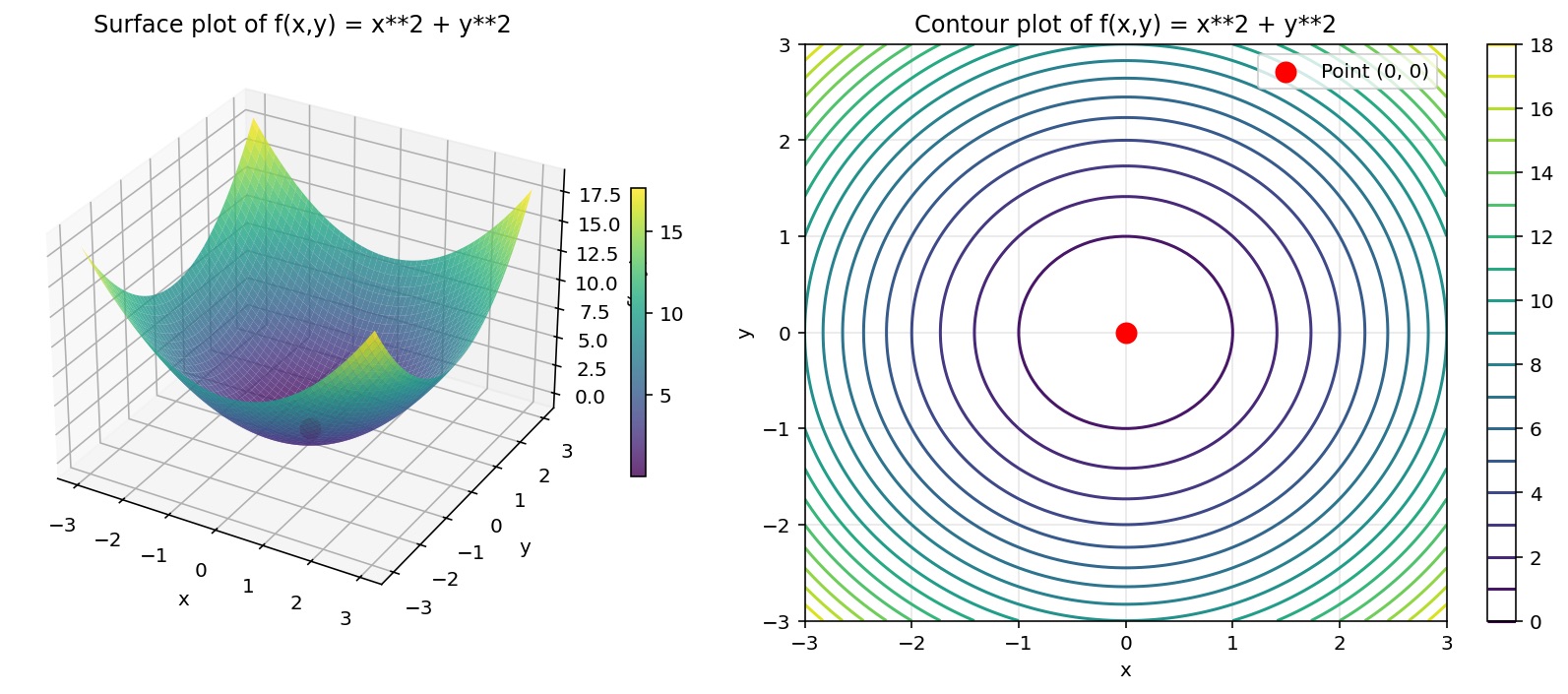
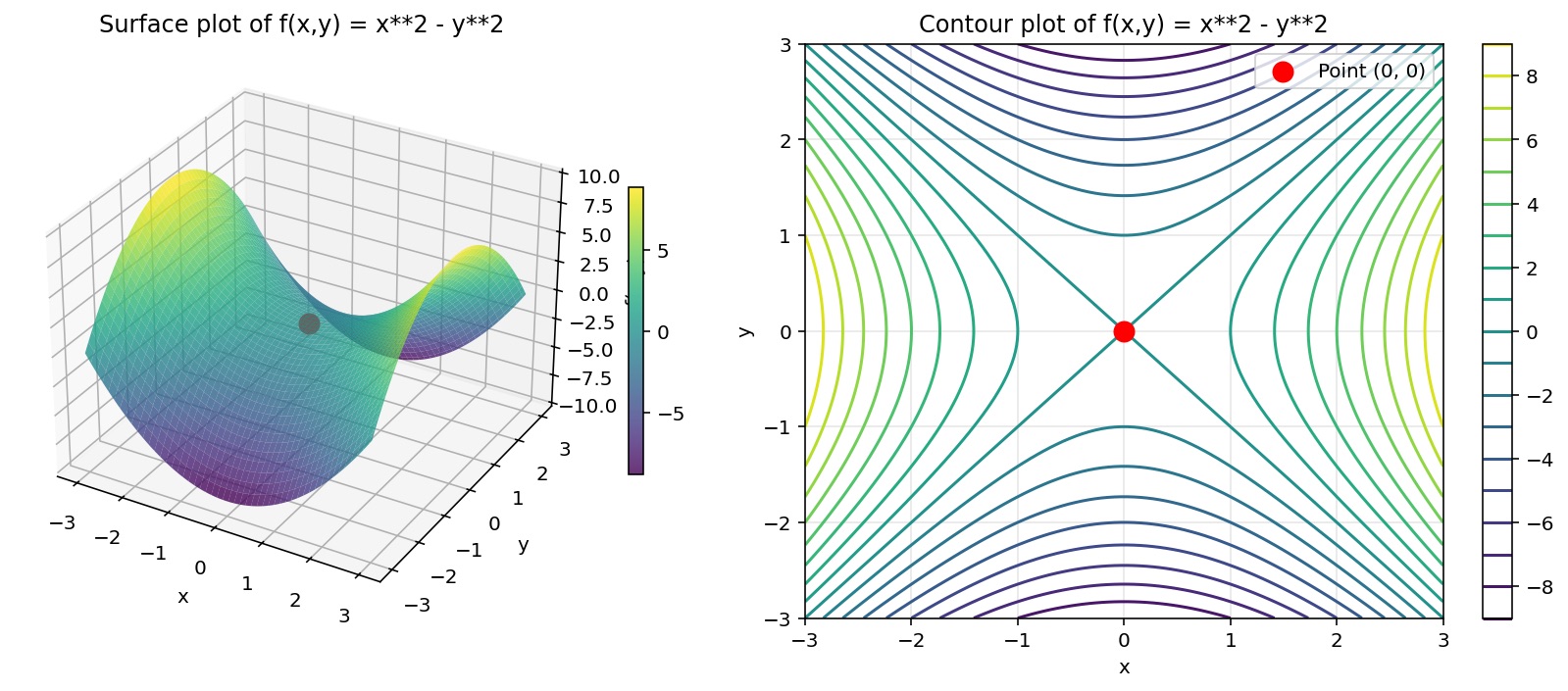
ax² + bxy + cy² :根据a、b和c的值,这可以是一个碗(都是正值),一个倒置的碗(都是负值),或者......一个马鞍形!
"一袋薯片"?没错!这就是广义二次型给你的一袋不同的曲面。碗状、山状、马鞍形,都用同一个紧凑公式描述,只是系数不同。然后, Hessian 矩阵会告诉你,你手里拿着的是哪种薯片!如果 Hessian 矩阵是"正定的",你就得到了一个碗。如果它是"负定的",你就得到了一个倒置的碗。如果两者都不是......你就得到了一个马鞍形。
"正定"(Positive definite),这个术语在优化、理解Hessian矩阵、区分芯片的过程中随处可见。
它的含义是:二次型(或表示它的矩阵)是"正定的",如果无论你选择哪个方向,v^T H v 的值始终为正,始终大于零。从几何学上讲,这意味着:无论你从临界点往哪个方向走,你都在上坡,每个方向都向上弯曲。这是一个碗状,一个局部最小值。
如果是"负定矩阵",那么 v^T H v 在任何方向上都为负,每条路径都向下。那就是山顶,局部最大值。
如果两者都不是......如果某些方向给出正值,而其他方向给出负值,那就是马鞍形。有些路径向上,有些路径向下。
关于"正定",我们知道它在概念上的含义,对于所有方向 v,v^T H v > 0。但我们需要一个实用的方法来验证它。有几种方法可以验证这一点:一种方法涉及"特征值",这是一个精彩的主题;另一种方法涉及研究某些子矩阵及其行列式。
特征值在某些方面更基础。它告诉你"主曲率",曲率的最强方向和最弱方向,这对于理解优化至关重要。但它们也更抽象,需要更多准备。行列式更具体,更具计算性。"计算一下,看看它是否为正。"但它们可能感觉更像是一个处方,而不是一种理解。