数据结构——二十九、图的广度优先遍历(BFS)(王道408)

文章目录

前言
一.与树的广度优先遍历之间的联系
二.代码实现
三.广度优先遍历序列
四.广度优先生成树
- 1.获得广度优先生成树的过程
- 2.总结
五.广度优先生成森林
六.练习：有向图的BFS过程
七.知识回顾与重要考点
结语

前言

本文探讨了图的广度优先遍历(BFS)算法。首先通过与树的广度优先遍历对比，指出两者在横向搜索节点方面的相似性，以及图遍历中可能遇到的环路问题。接着详细介绍了BFS的实现思路：使用访问标记数组、辅助队列和两个基本操作（FirstNeighbor和NextNeighbor）来获取相邻节点。代码实现部分展示了从初始顶点出发，依次访问并标记相邻顶点并入队的过程。通过示例图解说明了算法执行时队列和访问标记的动态变化，帮助理解BFS如何逐层探索图中的节点。文章系统性地阐述了BFS的核心概念和实现方法。
代码在文章开头,需要自取🧐

一.与树的广度优先遍历之间的联系

1.树的广度优先遍历(层序遍历)

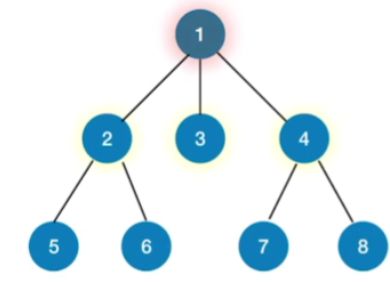
就是从根节点出发,找到和根节点相邻的所有节点,也就是2,3,4这几个节点
接下来再从2,3,4这几个节点出发,找到与他们相邻的其他节点,也就是5,6,7,8这几个节点,那这样就可以依次逐层的找到所有的树里边的节点

因为我们在查找这些节点的时候,都是尽可能的往横向的找,因此叫做广度优先遍历

2.图的广度优先遍历

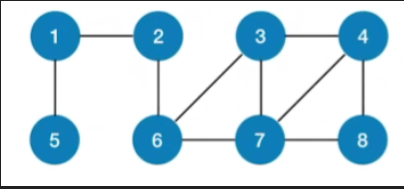
比如我们从这个2号节点出发开始进行广度优先遍历,那首先应该访问的是2号节点
那通过2号节点又可以找到下一层的1和6,所以接下来要访问的是1和6
那再往后应该从1和6出发,再找到与他们相邻近的其他节点,也就是5,3,7这几个节点,因此接下来访问的就应该是5,3,7
最后再从5,3,7这几个节点出发,再找到更下一层的节点,也就是4,8这两个节点,因此最后访问的是4,8

3.树和图的广度优先遍历的联系与区别

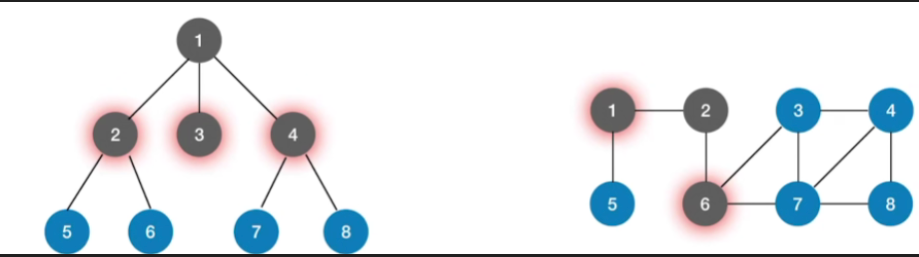
1.联系

不论是树还是图,在进行广度优先遍历的时候,我们都需要实现这样的一个操作,就是通过某一个节点找到与之相邻的其他节点(那对于树来说,要找到与一个节点相连的其他节点,其实就是找他的孩子,而对于图来说,我们可以利用上一章提到过的两个基本操作来完成这个事情)

2.区别

对于树这种数据结构,由于各个节点之间的路径是不可能存在环路,因此我们通过数理的某一个节点搜索其他的节点的时候,那搜到的这些节点一定是之前没有访问过的节点,但是对于图来说就不一样了,由于图里有可能出现这种环路环形的路径,因此在搜索相邻的顶点时，有可能搜到已经访问过的顶点

二.代码实现

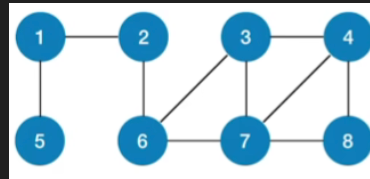
1.思路

广度优先遍历(Breadth-First-Search,BFS)要点：
1. 找到与一个顶点相邻的所有顶点
- 用到的基本操作:
  - FirstNeighbor(G,x):求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1。
  - NextNeighbor(G,x,y):假设图G中顶点y是顶点x的一个邻接点，返回除y之外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1。
1. 标记哪些顶点被访问过
- 用到的变量:
  - bool visited [MAX_VERTEX_NUM]; //访问标记数组
1. 需要一个辅助队列

2.代码实现

1.代码展示

c 复制代码

bool visited[MAX_VERTEX_NUM]; //访问标记数组
//广度优先遍历
void BFS(Graph G,int v){	//从顶点v出发，广度优先遍历图G
	visit(v);	//访问初始顶点v
	visited[v]=TRUE;	//对v做已访问标记
	EnQueue(Q,v);	//顶点v入队列Q
	while(!isEmpty(Q)){
		DeQueue(Q,v);	//顶点v出队列
		for(w=FirstNeighbor(G,w);w=0;w=NextNeighbor(G,v,w))
		//检测v所有邻接点
		if(!visited[w]){	//w为v的尚未访问的邻接顶点
			visit(w);	//访问顶点w
			visited[w]=TRUE;//对w做已访问标记
			EnQueue(Q,w);	//顶点w入队列
		}//if
	}//while
}

2.代码过程

如果我们从2号顶点出发,想要广度优先遍历整个图的话,那首先我们要访问2号节点,并且把2号节点对应的visit数组设为true,表示它已经被访问过了
接下来让2号节点入队
如果队列不空的话,那么我们就让队头的元素出队,也就是2号顶点出队,那接下来我们要通过2号顶点找到与之相邻的所有的顶点,那这个for循环(for(w=FirstNeighbor(G,y);w>=0;w=NextNeighbor(G,y,w)))就利用了我们刚才提到的那两个基本操作来便利与之相邻的所有的顶点,也就是1和6这两个顶点
那由于1和6的visit数组所对应的这个值都是false,也就是意味着他们俩没有被访问过,所以这两个顶点都会被正常的visit,并且会把它们俩对应的啊这个数组的值设为true,另外对于我们访问过的顶点还需要把它放到队列的队尾中
这个 for循环处理完了和2相邻的所有的顶点,那接下来就应该再进行下一次while循环,由于此时队列是非空的,那么需要让队头元素出队
接下来又到了这个for循环来处理1号节点相邻的所有的节点,和1号相邻的有2号和5号这两个节点,但是由于2号节点的visit值为true,也就意味着它已经被访问过了,因此对2号节点不会再进行其他的处理,对于5号结点和之前一样访问它,将其visit值设为true并且将其入队
后面的操作与之前一样,不再赘述,最终结果如图
- 其遍历序列为:

3.算法存在的问题

如果是非连通图，则无法遍历完所有结点

4.改进

1.思路

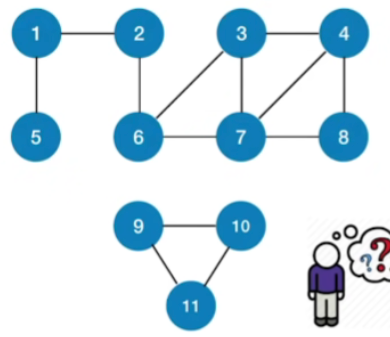
通过visit数组里面存储的是否被访问的信息,就可以知道是否还有结点未被访问

2.代码展示

c 复制代码

bool visited[MAX_VERTEX_NUM]; //访问标记数组

void BFSTraverse(Graph G){//对图G进行广度优先遍历
	for(i=1; i<G.vexnum;++i)//访问标记数组初始化
		visited[i]=FALSE;
	InitQueue(Q);//初始化辅助队列Q
	for(i=1; i<G.vexnum;++i)//从0号顶点开始遍历
		if(!visited[i])//对每个连通分量调用一次BFS
			BFS(G,i);//vi未访问过，从vi开始BFS
}

//广度优先遍历
void BFS(Graph G,int v){	//从顶点v出发，广度优先遍历图G
	visit(v);	//访问初始顶点v
	visited[v]=TRUE;	//对v做已访问标记
	EnQueue(Q,v);	//顶点v入队列Q
	while(!isEmpty(Q)){
		DeQueue(Q,v);	//顶点v出队列
		for(w=FirstNeighbor(G,w);w!=0;w=NextNeighbor(G,v,w))
		//检测v所有邻接点
		if(!visited[w]){	//w为v的尚未访问的邻接顶点
			visit(w);	//访问顶点w
			visited[w]=TRUE;//对w做已访问标记
			EnQueue(Q,w);	//顶点w入队列
		}//if
	}//while
}

额外设置一个函数来判断visit数组中的元素是否已经被访问,如果没有,则调用BFS函数进行遍历
显然,对于无向图，调用BFS函数的次数=连通分量数

3.复杂度分析

广度优先和深度优先这两种算法,算法的时间开销主要来自于访问顶点和找各条边,因此在分析这两种算法的时间复杂度的时候,最好不要看最深层循环的次数,而是将问题简化为访问顶点和找各条边的时间开销

1.空间复杂度

最坏空间复杂度
- 辅助队列大小为O(|V|)

2.时间复杂度

1.邻接矩阵存储的图

访问 |V| 个顶点需要O(|V|)的时间
查找每个顶点的邻接点都需要O(|V|)的时间，而总共有|V|个顶点
时间复杂度= O(|V|²)

2.邻接表存储的图

访问|V|个顶点需要O(|V|)的时间
查找各个顶点的邻接点共需要O(2|E|)的时间,时间复杂度可以舍弃2这个常数,即O(|E|)
时间复杂度=O(|V|+|E|)

三.广度优先遍历序列

1.学会按照代码的思路手搓广度优先遍历序列

从顶点1出发得到的广度优先遍历序列：
1, 2, 5, 6, 3, 7, 4, 8
从顶点3出发得到的广度优先遍历序列：
3, 4, 6, 7, 8, 2, 1, 5

2.遍历序列的可变性

1.采用邻接矩阵

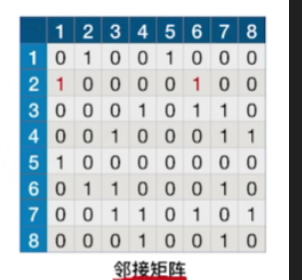
找到顶点后找其相邻接的顶点一定是递增次序的
如找到3这个顶点后,找其邻接顶点的顺序一定是4,6,7

2.采用邻接表

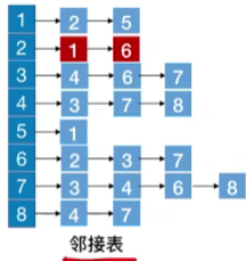
次序不确定,要看相应的顶点对结点的存储的地方,是随机存储的,不具有固定规律
比如说对于2号节点
- 图中显示的存储顺序为1,6
- 但是,如果我是用的头插法插入结点,那么其结点顺序会变为:6,1,那么在找其邻接顶点时,就不是升序了

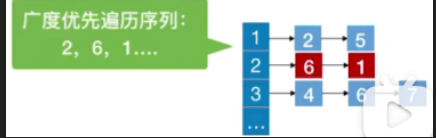
总结

同一个图的邻接矩阵表示方式唯一，因此广度优先遍历序列唯一
同一个图邻接表表示方式不唯一，因此广度优先遍历序列不唯一

四.广度优先生成树

1.获得广度优先生成树的过程

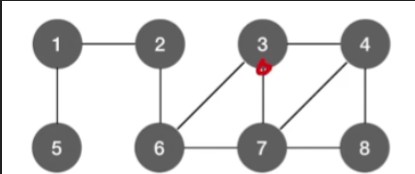
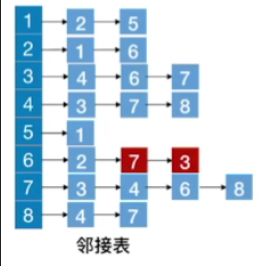
存储图的邻接表
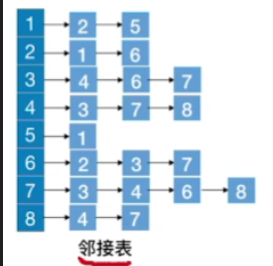
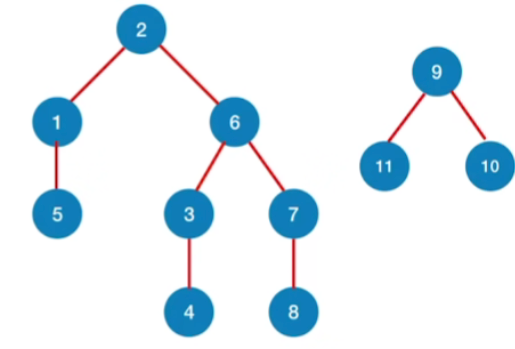
以2为顶点获得的广度优先遍历的路径(标红线)
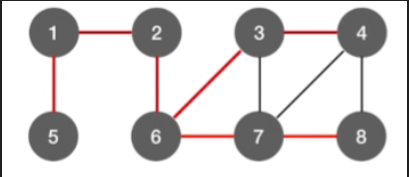
去掉黑线,得到广度优先生成树
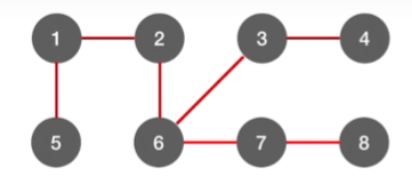
换一种画法,使其更像树结构
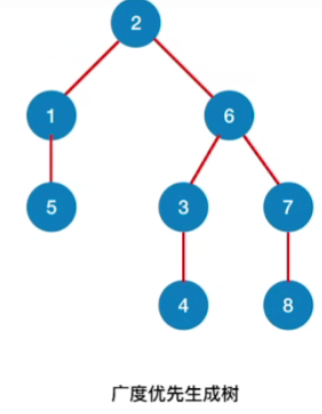
现在更改邻接表,按照上面的方法得到广度优先生成树

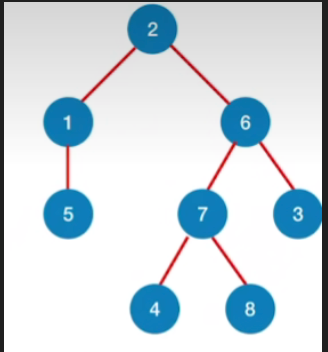
2.总结

广度优先生成树由广度优先遍历过程确定。由于邻接表的表示方式不唯一，因此基于邻接表的广度优先生成树也不唯一。

五.广度优先生成森林

非连通图
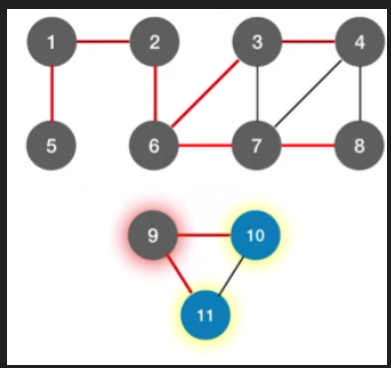
每个连通分量通过广度优先生成树的方法生成一个单独的树,每个树合起来就组成了广度优先生成森林

六.练习：有向图的BFS过程

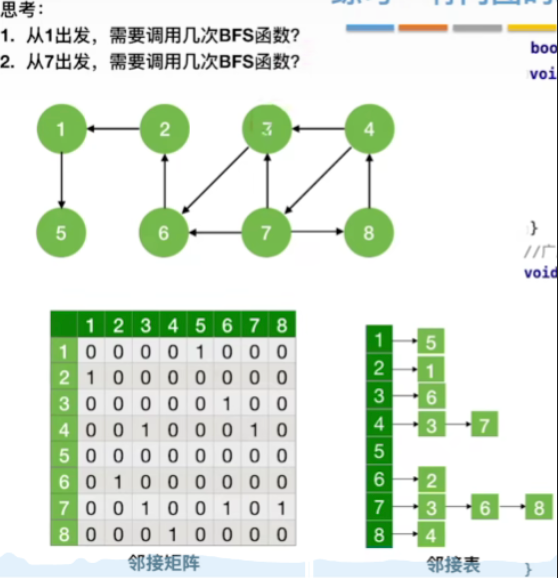
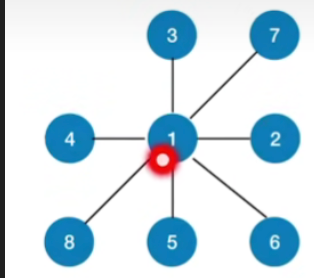
从1出发:
1. 第一次调用BFS,1->5,这时回到BFSTraverse函数
2. 第二次调用BFS是以2为起始,2->1,且1已经被访问过,因此回到BFSTraverse函数
3. 第三次调用BFS是以3为起始,3->6->2,2已被访问过,因此回到BFSTraverse函数
4. 第四次调用BFS是以4为起始,4->3,3已被访问,但是4还有一个出度4,执行4->7,接下来以7为顶点,除已经被访问的顶点3,6,可访问到7->8,接下来以8为顶点,8的出度4已经被访问,因此回到BFSTraverse函数
5. 可以发现所有顶点已经被访问了,结果就是调用了4次BFS函数
从7出发:
1. 分析方法一样,就直接给结果了:1次BFS函数

七.知识回顾与重要考点

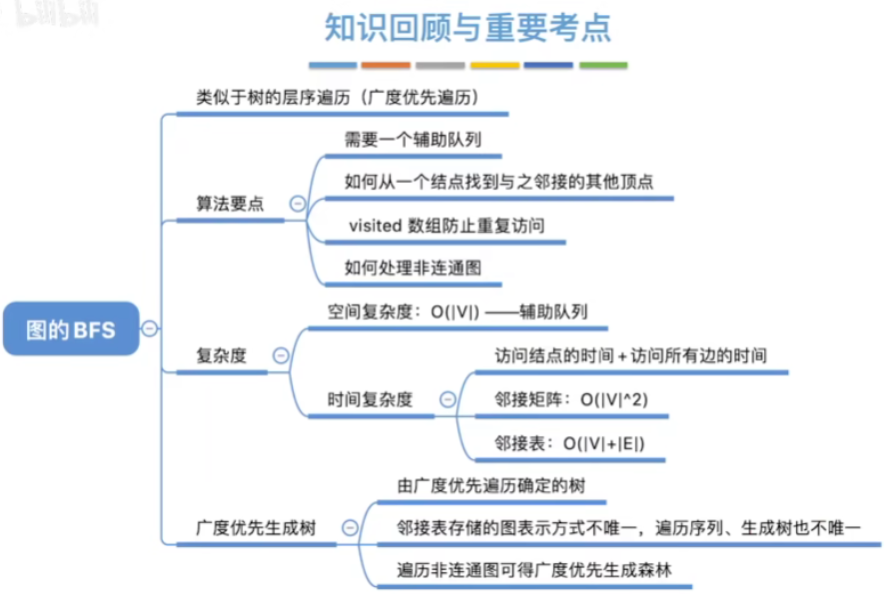
结语

一更😁
如果想查看更多章节,请点击:一、数据结构专栏导航页