一、梯度下降的实现（Gradient Descent Implementation）
在训练模型时，我们的目标是最小化代价函数（Cost Function） 。
梯度下降是一种常用的优化算法，通过不断调整参数 w,b，让代价函数 J(w,b) 逐渐逼近最小值。
1. 算法思想
梯度下降算法的核心思想是：
从某一点出发，沿着函数下降最快的方向（即负梯度方向）前进，直到到达最小值。
更新规则为：
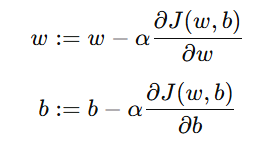
其中：
-
α 为 学习率（Learning Rate）
-
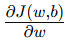为 梯度（Gradient）
2. 线性回归与逻辑回归中的区别
虽然线性回归与逻辑回归都使用梯度下降算法，但它们的代价函数与导数不同：
| 模型 | 预测函数 | 代价函数 | 特点 |
|---|---|---|---|
| 线性回归 |  |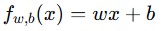
 |
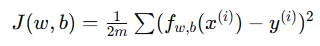使用平方误差，函数为凸函数 |
| 逻辑回归 |  |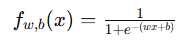
 |
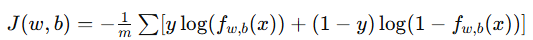使用对数损失，函数为凸函数 |
二者的梯度下降形式一致，但梯度计算方式不同。
二、过拟合的问题（Overfitting Problem）
1. 概念
过拟合（Overfitting） 是指模型在训练数据上表现很好，但在测试数据上表现很差。即模型"记住"了训练数据的特征，而没有学会通用的规律。
2. 举例说明
假设我们要使用线性模型预测房价。
| 面积（x） | 房价（y） |
|---|---|
| 50 | 100 |
| 60 | 120 |
| 70 | 140 |
| 80 | 160 |
| 90 | 180 |
-
使用线性回归模型（一次多项式）：
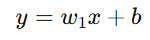
→ 模型可能欠拟合（Underfitting），无法捕捉复杂变化。
-
使用二次多项式模型：
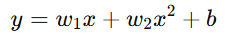
→ 更好地拟合数据，误差降低。
-
使用四次多项式模型：
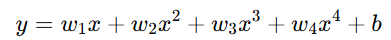
→ 几乎完美地通过每个点（训练误差为0），但在新样本上波动剧烈，泛化能力极差。
这就是典型的过拟合现象。
同样地，过拟合问题也会出现在分类任务中。例如：
-
模型在训练集上能精确分类每个点；
-
但在测试集上预测错误率非常高。
三、解决过拟合的方法（How to Reduce Overfitting）
方法一：增加训练数据
获取更多样化的训练数据，能帮助模型学习到更真实的分布，减少过度拟合噪声的风险。
方法二：减少特征数量
-
移除不相关或冗余特征；
-
避免使用过高阶多项式；
-
选择有代表性的关键特征。
这相当于"让模型变简单"，降低复杂度。
方法三：正则化（Regularization）
正则化是一种通过约束参数大小来防止过拟合的方法。我们不直接删除特征，而是让参数的值尽量小。
1. 正则化思想
在代价函数中加入一个"惩罚项"，鼓励参数 wiw_iwi 变小。
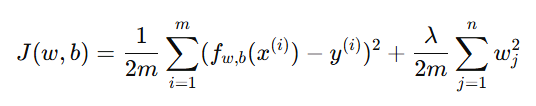
其中：
-
λ 是正则化参数（Regularization Parameter）
-
惩罚项
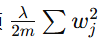防止权重过大
2. 正则化更新规则（线性回归）
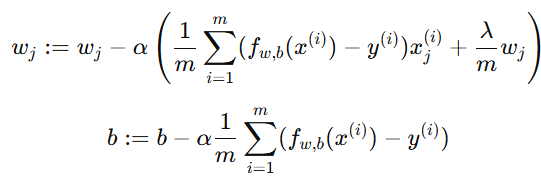
方法四：特征选择（Feature Selection）
有些情况下，我们可以直接去除权重较小或不重要的特征（相当于让参数为0），进一步简化模型。
总结
| 过拟合原因 | 解决思路 |
|---|---|
| 模型太复杂 | 减少特征数量、使用正则化 |
| 数据太少 | 增加训练样本 |
| 参数太多 | 使用较小的多项式或正则化项 |
| 学习噪声 | 数据清洗、平滑处理 |