一.算法背景
Adam(Adaptive Moment Estimation)是一种广泛应用于深度学习模型训练的自适应优化算法,由Diederik P. Kingma和Jimmy Lei Ba于2014年提出,旨在解决传统优化算法在深度学习中的局限性。它融合了Momentum动量优化器和RMSProp动态自适应学习率优化器两种主流优化技术的优势。
二.数学公式
Adam优化器通过计算梯度的一阶矩(均值)和二阶矩(方差)来为每个参数自适应地调整学习率。其数学实现步骤如下:
一阶矩阵估计(动量项,类似于动量优化器中的动量计算,记录梯度的指数加权平均值):
二阶矩阵估计(自适应学习率项,类似于RMSProp,记录梯度平方的指数加权平均值):
偏差修正(下面会说为什么要做这个):
参数更新(和前几个优化器的更新流程一样):
代码实现如下:
python
import numpy as np
from collections import OrderedDict
import matplotlib.pyplot as plt
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
optimizers= Adam(lr=0.3)
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
x_history = []
y_history = []
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizers.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
idx = 1
# plot
plt.subplot(2, 2, idx)
idx += 1
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
# colorbar()
# spring()
plt.title("Momentum")
plt.xlabel("x")
plt.ylabel("y")
plt.show()运行结果如下:
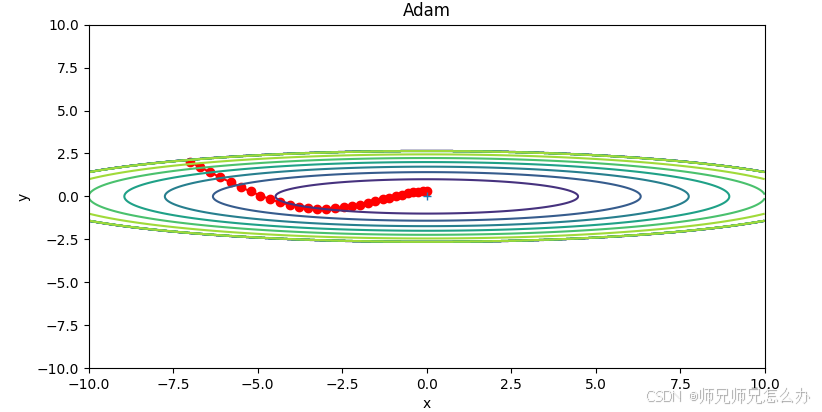
三.为什么要进行偏差修正
它解决了指数加权平均在初始阶段的估计偏差问题。Adam优化器使用指数加权移动平均(EWMA)来计算梯度的一阶矩(m)和二阶矩(v)估计。在初始阶段,这些估计值会存在系统性偏差,原因在于:
-
初始化问题 :m和v通常初始化为0向量,导致初始估计明显偏低,在t较小时,
接近于0,导致未修正的m和v远小于真实梯度统计量,计算出的学习率会异常偏大。
-
指数加权特性:早期时间步的估计值受初始值影响较大, 修正项随着t的增加逐渐趋近于1,在训练后期影响变小,但在初期至关重要。
-
**训练不稳定:**参数更新幅度在初期波动剧烈,可能错过合理的优化方向,增加收敛到次优解的风险,需要更多迭代次数才能克服初始偏差,特别是在稀疏梯度问题上表现更差。
进行偏差修正后,从第一轮迭代就开始积累有意义的梯度统计量,加速模型早期的学习过程,减少对初期学习率的敏感度,使默认参数**(β₁=0.9, β₂=0.999)**在大多数情况下都能良好工作。
误差修正通过以下数学公式实现:
其中:
-
和
是衰减率(通常取0.9和0.999)
-
是当前时间步(迭代次数)
-
和
是未修正的矩估计
以下使用代码对不进行偏差修正和进行偏差修正的参数更新轨迹和损失函数收敛的对比:
python
import numpy as np
import matplotlib.pyplot as plt
class AdamWithCorrection:
"""带误差修正的Adam优化器"""
def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8):
self.learning_rate = learning_rate
self.beta1 = beta1
self.beta2 = beta2
self.epsilon = epsilon
self.m = None
self.v = None
self.t = 0
self.history = {'params': [], 'loss': []}
def update(self, params, grads, loss):
if self.m is None:
self.m = np.zeros_like(params)
self.v = np.zeros_like(params)
self.t += 1
self.m = self.beta1 * self.m + (1 - self.beta1) * grads
self.v = self.beta2 * self.v + (1 - self.beta2) * (grads ** 2)
# 误差修正
m_hat = self.m / (1 - self.beta1 ** self.t)
v_hat = self.v / (1 - self.beta2 ** self.t)
params -= self.learning_rate * m_hat / (np.sqrt(v_hat) + self.epsilon)
self.history['params'].append(params.copy())
self.history['loss'].append(loss)
return params
class AdamWithoutCorrection:
"""不带误差修正的Adam优化器"""
def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8):
self.learning_rate = learning_rate
self.beta1 = beta1
self.beta2 = beta2
self.epsilon = epsilon
self.m = None
self.v = None
self.t = 0
self.history = {'params': [], 'loss': []}
def update(self, params, grads, loss):
if self.m is None:
self.m = np.zeros_like(params)
self.v = np.zeros_like(params)
self.t += 1
self.m = self.beta1 * self.m + (1 - self.beta1) * grads
self.v = self.beta2 * self.v + (1 - self.beta2) * (grads ** 2)
# 无误差修正
params -= self.learning_rate * self.m / (np.sqrt(self.v) + self.epsilon)
self.history['params'].append(params.copy())
self.history['loss'].append(loss)
return params
# 定义优化问题
def loss_function(x):
return np.sum(0.5 * x**2) # 简单的二次函数
def gradient_function(x):
return x # 梯度就是x本身
# 初始化参数
params_corr = np.array([3.0, -2.0])
params_no_corr = params_corr.copy()
# 初始化优化器
optimizer_corr = AdamWithCorrection(learning_rate=0.1)
optimizer_no_corr = AdamWithoutCorrection(learning_rate=0.1)
# 优化过程
for i in range(100):
grads_corr = gradient_function(params_corr)
grads_no_corr = gradient_function(params_no_corr)
loss_corr = loss_function(params_corr)
loss_no_corr = loss_function(params_no_corr)
params_corr = optimizer_corr.update(params_corr, grads_corr, loss_corr)
params_no_corr = optimizer_no_corr.update(params_no_corr, grads_no_corr, loss_no_corr)
# 可视化结果
plt.figure(figsize=(15, 5))
# 1. 参数轨迹对比
plt.subplot(1, 2, 1)
params_history_corr = np.array(optimizer_corr.history['params'])
params_history_no_corr = np.array(optimizer_no_corr.history['params'])
plt.plot(params_history_corr[:, 0], params_history_corr[:, 1], label='With Correction', color='blue')
plt.plot(params_history_no_corr[:, 0], params_history_no_corr[:, 1], label='Without Correction', color='red')
plt.scatter([0], [0], color='green', marker='*', s=200, label='Optimal Point')
plt.title('Parameter Trajectory Comparison')
plt.xlabel('Parameter 1')
plt.ylabel('Parameter 2')
plt.legend()
plt.grid(True)
# 2. 损失曲线对比
plt.subplot(1, 2, 2)
plt.plot(optimizer_corr.history['loss'], label='With Correction', color='blue')
plt.plot(optimizer_no_corr.history['loss'], label='Without Correction', color='red')
plt.title('Loss Convergence Comparison')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()运行代码可以清晰地看到两者之间的区别:
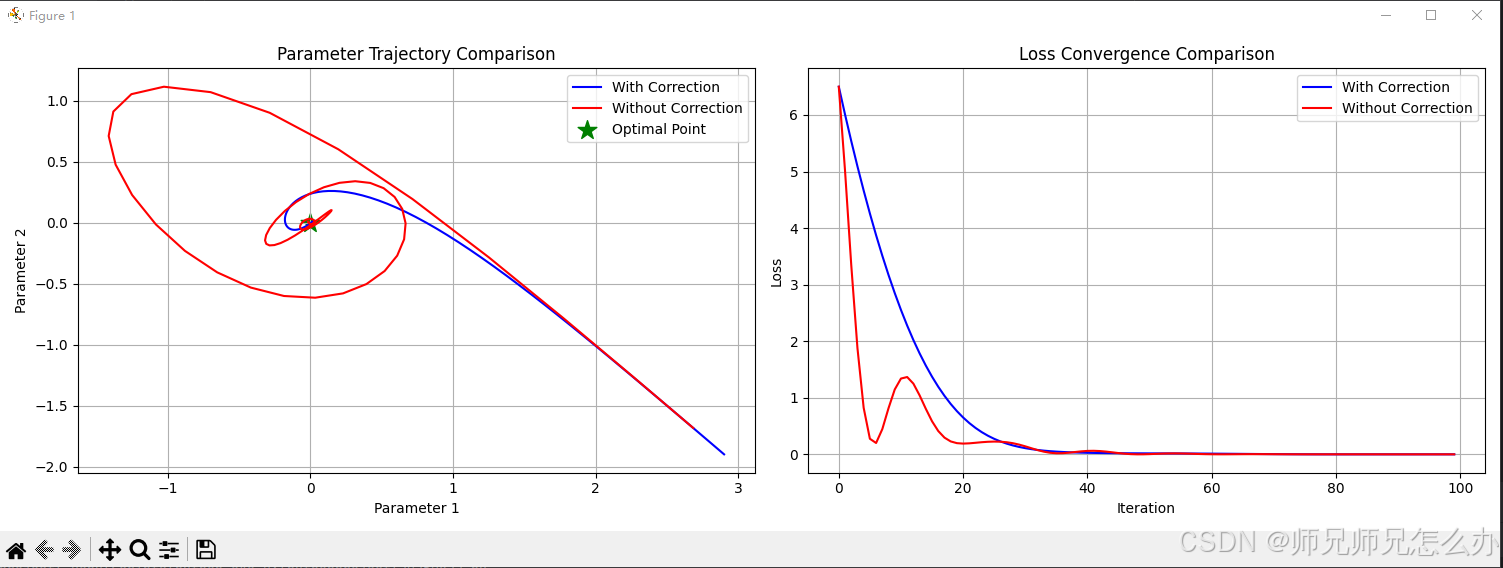
四.和其他优化器的对比
与其他优化器的对比:
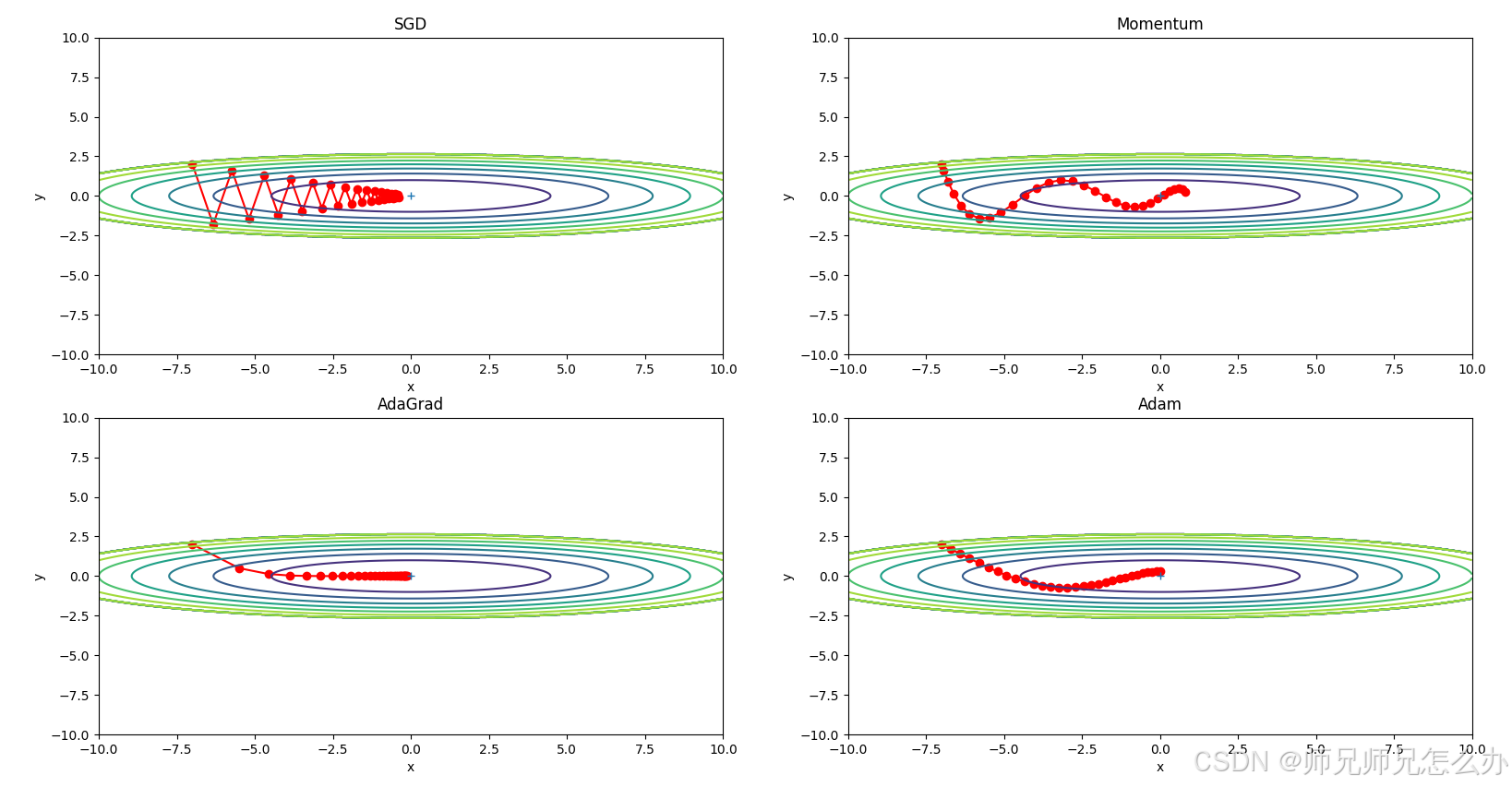
特点对比:
| 特性 | Adam | SGD | Momentum | RMSProp |
|---|---|---|---|---|
| 自适应学习率 | ✓ | ✗ | ✗ | ✓ |
| 动量机制 | ✓ | ✗ | ✓ | ✗ |
| 参数独立调整 | ✓ | ✗ | ✗ | ✓ |
| 偏差修正 | ✓ | ✗ | ✗ | ✗ |
| 收敛速度 | 快 | 慢 | 中等 | 中等 |
| 超参数数量 | 4 | 1 | 2 | 3 |