论文笔记（九十六）VGGT: Visual Geometry Grounded Transformer

VGGT: Visual Geometry Grounded Transformer

文章概括
Abstract
[1. 引言](#1. 引言)
[2. 相关工作](#2. 相关工作)
[3. 方法](#3. 方法)
- [3.1 问题定义与符号](#3.1 问题定义与符号)
- [3.2 特征骨干](#3.2 特征骨干)
- [3.3 预测头](#3.3 预测头)
[4. 实验](#4. 实验)
- [4.1 相机位姿估计](#4.1 相机位姿估计)
- [4.2 多视图深度估计](#4.2 多视图深度估计)
- [4.3 点图估计](#4.3 点图估计)
- [4.4 图像匹配](#4.4 图像匹配)
- [4.5 消融实验](#4.5 消融实验)
- [4.6 下游任务的微调](#4.6 下游任务的微调)
[5. 结论](#5. 结论)

文章概括

引用：

bash 复制代码

@inproceedings{wang2025vggt,
  title={Vggt: Visual geometry grounded transformer},
  author={Wang, Jianyuan and Chen, Minghao and Karaev, Nikita and Vedaldi, Andrea and Rupprecht, Christian and Novotny, David},
  booktitle={Proceedings of the Computer Vision and Pattern Recognition Conference},
  pages={5294--5306},
  year={2025}
}

markup 复制代码

Wang, J., Chen, M., Karaev, N., Vedaldi, A., Rupprecht, C. and Novotny, D., 2025. Vggt: Visual geometry grounded transformer. In Proceedings of the Computer Vision and Pattern Recognition Conference (pp. 5294-5306).

主页：
原文： https://openaccess.thecvf.com/content/CVPR2025/html/Wang_VGGT_Visual_Geometry_Grounded_Transformer_CVPR_2025_paper.html
代码、数据和视频：

系列文章：

请在《《《文章》》》专栏中查找

宇宙声明！

引用解析部分属于自我理解补充，如有错误可以评论讨论然后改正！

Abstract

我们提出VGGT ，这是一种前馈神经网络 ，能够直接从场景的一张、几张，甚至上百张视图中，推断出该场景的所有关键3D属性 ，包括相机参数 、点图、深度图 以及3D点轨迹 。在3D计算机视觉 领域中，模型通常受限并专门用于单一任务 ；而我们的方法向前迈出了一步。该方法简单高效 ，图像重建时间不足一秒 ，并且即便无需 视觉几何优化的后处理 ，其表现仍优于那些需要此类后处理的替代方法。该网络在多项3D任务 上取得了最先进（SOTA）的结果 ，包括相机参数估计 、多视图深度估计 、稠密点云重建 以及3D点跟踪 。我们还表明，使用预训练的VGGT 作为特征骨干 ，能显著提升 下游任务的性能，例如非刚性点跟踪 和前馈式新视角合成 。代码和模型已公开，见：https://github.com/facebookresearch/vggt。

图1。 VGGT 是一个大型前馈式 Transformer，仅包含极少的三维归纳偏置，并在海量带三维标注的数据上训练得到。

1. 引言

我们研究这样一个问题：利用前馈神经网络 ，从一组图像中估计该场景的三维属性 。传统上，三维重建 主要采用视觉几何 方法，并使用诸如束调整 （Bundle Adjustment, BA）[33] 之类的迭代优化 技术。机器学习 常常扮演重要的互补角色，解决单靠几何无法完成的任务，例如特征匹配 与单目深度预测 。这种融合日益紧密；目前，像 VGGSfM [83] 这样的最先进 运动恢复结构（SfM ）方法，通过可微BA 将机器学习与视觉几何端到端 结合起来。即便如此，视觉几何仍在三维重建中占据主导地位 ，这会带来更高的复杂度 与计算成本。

想象有几张不同角度的照片，我们知道每张照片上某些像素点对应同一个真实世界点。如果我们猜出每个相机的姿态和每个3D点的位置，我们可以把那个3D点投影回每张图像，看看它投影的位置与真实像素的差距（误差）。

BA 要做的就是：
\quad 调整（Bundle）所有这些变量（相机姿态+3D点），让这些误差（Adjustment）整体最小。

随着网络能力不断增强，我们提出一个问题：三维任务 是否终于可以直接由神经网络 解决，从而几乎完全摒弃几何后处理？近期的工作，如 DUSt3R [87] 及其演化版 MASt3R [43]，在这一方向上展示了可喜成果，但这些网络一次只能处理两张图像，并且需要依赖后处理来重建更多图像，即通过融合成对重建的方式实现。

在本文中，我们更进一步，力图消除在后处理中优化三维几何的需求。为此，我们提出Visual Geometry Grounded Transformer（VGGT），这是一种前馈神经网络，可从一张、几张，甚至上百张场景视图中进行三维重建。VGGT能够预测完整的三维属性集合，包括相机参数、深度图、点图（point maps，逐像素3D点坐标图）以及三维点轨迹。这些预测在一次前向传播内即可完成，耗时仅需数秒。值得注意的是，即使无需进一步处理，它的表现也常常优于基于优化的替代方法。这与 DUSt3R、MASt3R 或 VGGSfM 存在显著差异------这些方法仍需要代价高昂的迭代式后优化才能得到可用结果。

我们还表明，三维重建不必设计专用网络架构。相反，VGGT基于一个相当标准的大型Transformer [79]，不包含特殊的三维或其他归纳偏置（除了在帧级注意力与全局注意力之间交替），并在大量公开三维标注数据集上进行训练。因此，VGGT与自然语言处理和计算机视觉领域的大模型采用了同样的范式，如 GPTs [1,18,101]、CLIP [56]、DINO [6,53] 与 Stable Diffusion [22]。这些模型已成为通用骨干，可以通过微调来解决新的、特定的任务。类似地，我们表明，VGGT提取的特征能够显著提升下游任务的表现，例如动态视频中的点跟踪与新视角合成。

近年来出现了一些大型三维神经网络的例子，包括 DepthAnything [97]、MoGe [86] 和 LRM [34]。然而，这些模型通常只关注单一的三维任务，例如单目深度估计或新视角合成。相较之下，VGGT采用共享骨干，联合预测所有感兴趣的三维量。我们证明：尽管这些三维属性之间可能存在冗余，但联合学习这些相互关联的属性能够提升整体精度。同时，我们还表明：在推理阶段，可以通过单独预测的深度与相机参数来推导出点图，其精度优于直接使用专门的点图头。

总之，我们的贡献如下：（1）我们提出VGGT，一个大型前馈式Transformer，在给定一张、几张，甚至上百张场景图像的情况下，能够在数秒内预测所有关键三维属性，包括相机内参与外参、点图、深度图以及三维点轨迹。（2）我们证明，VGGT的预测可直接使用，表现极具竞争力，通常优于那些依赖缓慢后处理优化的最先进方法。（3）我们还表明，将VGGT与BA后处理进一步结合时，它能够在各项任务上取得全面的SOTA成绩；即便与专注于部分三维任务的方法相比，也大幅提升结果质量。

2. 相关工作

运动恢复结构（SfM） 是计算机视觉中的经典问题[33,52,54]，其目标是从不同视角拍摄的静态场景图像集合中，估计相机参数并重建稀疏点云。传统的 SfM 流水线[2,24,48,62,68,92]包含多个阶段，包括图像匹配、三角化以及束调整（Bundle Adjustment, BA）。COLMAP[62] 是基于该传统流程最流行的框架。近年来，深度学习改进了 SfM 流程中的许多组件，其中关键点检测[12,19,76,102]与图像匹配[7,46,60,66]是两个主要关注方向。近期方法[3,67,71,74,75,78,81,83,89,108]探索了端到端可微的 SfM，其中 VGGSfM[83] 已在具有挑战性的"摄影旅游（phototourism）"场景上开始超越传统算法。

多视图立体（MVS） 旨在从多幅重叠图像中稠密重建场景几何，通常假定相机参数已知，而这些参数往往由 SfM 估计得到。MVS 方法可分为三类：传统手工设计[26,27,64,88]、全局优化[25,50,91,100]与学习驱动方法[30,49,55,99,106]。与 SfM 类似，学习驱动的 MVS近来也取得了大量进展。其中，DUSt3R[87] 与 MASt3R[43] 能从一对视图直接估计对齐的稠密点云，与 MVS 类似，但不需要相机参数。一些同期工作[73,85,96,105]尝试以神经网络替代 DUSt3R 的测试时优化，但这些尝试的效果仅为次优或与 DUSt3R 相当。相比之下，VGGT相较 DUSt3R 与 MASt3R 大幅领先。

Tracking-Any-Point 最早由 Particle Video[59] 提出，并在深度学习时代由 PIPs[32] 重新激活，其目标是在视频序列中跟踪任意兴趣点，包括处理动态运动。给定一个视频与若干二维查询点，该任务需预测这些点在其他所有帧中的二维对应位置。TAP-Vid[13] 为该任务提出了三个基准，随后 TAPIR[14] 在一个简单基线上进行了改进。CoTracker[37,38] 利用点间相关性实现遮挡情况下的跟踪，而 DOT[41] 则实现了稠密点在遮挡下的跟踪。最近，TAPTR[44] 为该任务提出了端到端 Transformer，LocoTrack[8] 则将常用的逐点特征扩展到邻域区域。在此，我们表明，当与现有点跟踪器结合时，VGGT的特征能够带来最先进（SOTA）的跟踪性能。

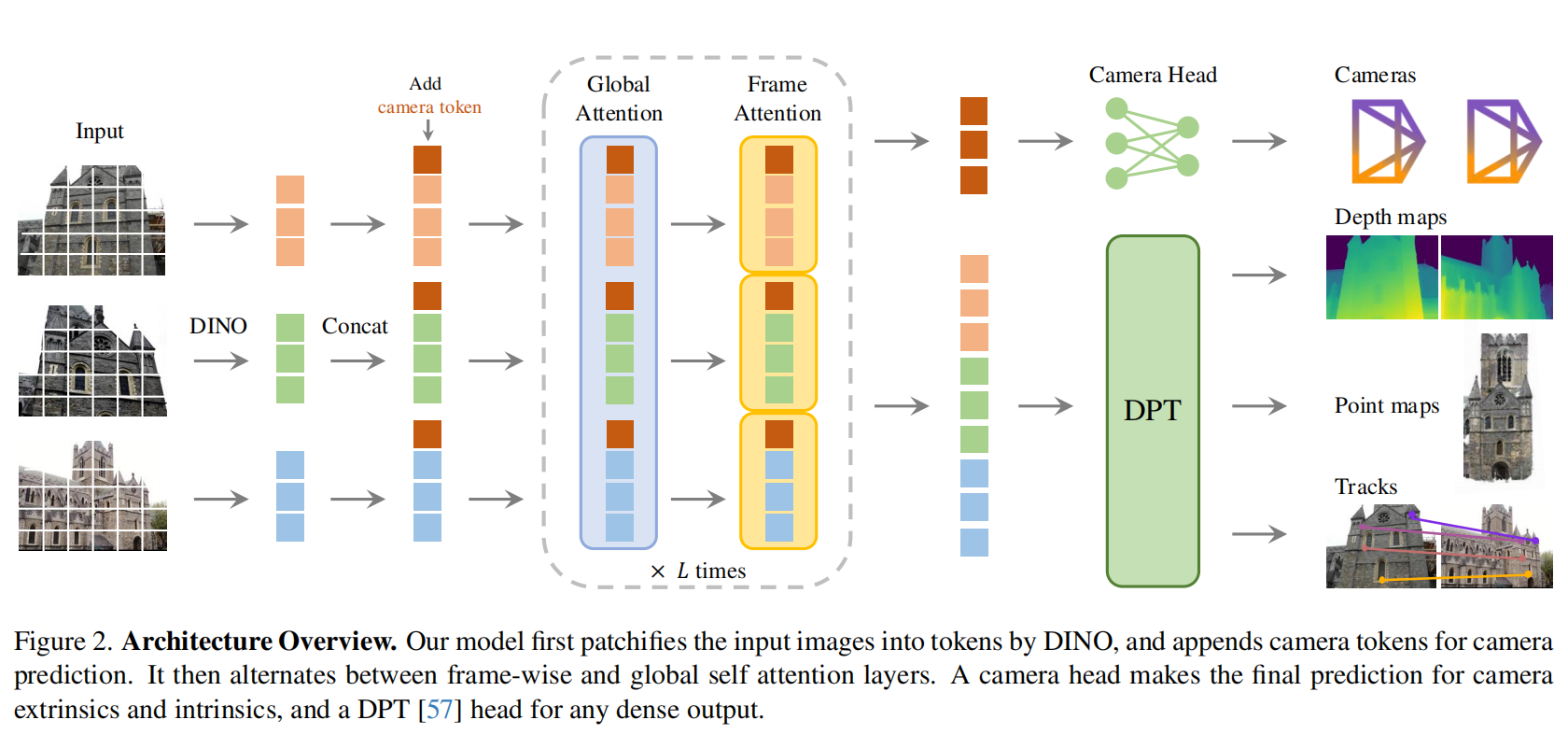图2。架构总览。我们的模型首先用 DINO 将输入图像切块并标记化为 tokens，并附加相机 tokens以进行相机预测。

3. 方法

我们提出VGGT，这是一种大型Transformer，输入是一组图像，输出为多种三维量。我们首先在第3.1节给出问题定义，然后在第3.2节介绍模型架构，并在第3.3节说明各预测头。

3.1 问题定义与符号

输入为 N N N 张RGB图像序列 ( I i ) i = 1 N (I_i)_{i=1}^N (Ii)i=1N，每张 I i ∈ R 3 × H × W I_i\in\mathbb{R}^{3\times H\times W} Ii∈R3×H×W，观测同一三维场景。VGGT 的 Transformer是一个函数，将该序列映射为逐帧的三维标注集合：

有 N N N 张图片（ I 1 , I 2 , . . . , I N I_1, I_2, ..., I_N I1,I2,...,IN）；每张都是普通的彩色图（3通道，尺寸 H × W H\times W H×W）；这些图像拍摄的是同一个三维场景，只是角度或位置不同。

f ( ( I i ) i = 1 N ) = ( g i , D i , P i , T i ) i = 1 N . (1) f\big((I_i)_{i=1}^N\big)=\big(\mathbf{g}i,D_i,P_i,T_i\big){i=1}^N.\tag{1} f((Ii)i=1N)=(gi,Di,Pi,Ti)i=1N.(1)

因此，Transformer将每张图像 , I i ,I_i ,Ii映射为：相机参数 g i ∈ R 9 \mathbf{g}_i\in\mathbb{R}^9 gi∈R9 （内参与外参）、深度图 D i ∈ R H × W D_i\in\mathbb{R}^{H\times W} Di∈RH×W、点图 P i ∈ R 3 × H × W P_i\in\mathbb{R}^{3\times H\times W} Pi∈R3×H×W，以及用于点跟踪的 C C C 维特征网格 T i ∈ R C × H × W T_i\in\mathbb{R}^{C\times H\times W} Ti∈RC×H×W 。下面说明其定义。

点云（Point Cloud）：一组在 3D 空间中的离散点集合，每个点有 ( x , y , z ) (x,y,z) (x,y,z) 坐标（有时带颜色/法线）通常是无序的列表： ( x j , y j , z j ) j = 1 M {(x_j,y_j,z_j)}_{j=1}^M (xj,yj,zj)j=1M

点图（Point Map / 3D point map）：对应每个图像像素 ( u , v ) (u,v) (u,v) 的 3D 坐标 ( X , Y , Z ) (X,Y,Z) (X,Y,Z) 有序的张量： P ∈ R 3 × H × W P\in\mathbb{R}^{3\times H\times W} P∈R3×H×W

每个像素都有一个 C C C 维的向量表示；它是网络为每个点学到的"语义或几何特征"；后续模块可以用这些特征在不同视角之间找"对应点"（tracking）。

相机参数 g i \mathbf{g}_i gi 采用[83]的参数化，记 g = [ q , t , f ] \mathbf{g}=[\mathbf{q},\mathbf{t},\mathbf{f}] g=[q,t,f]，其中 q ∈ R 4 \mathbf{q}\in\mathbb{R}^4 q∈R4 为旋转四元数， t ∈ R 3 \mathbf{t}\in\mathbb{R}^3 t∈R3 为平移向量， f ∈ R 2 \mathbf{f}\in\mathbb{R}^2 f∈R2为视场参数。我们假设相机主点位于图像中心，这在SfM框架中很常见[63,83]。

记图像 I i I_i Ii 的像素域为 I ( I i ) = { 1 , ... , H } × { 1 , ... , W } \mathcal{I}(I_i)=\{1,\ldots,H\}\times\{1,\ldots,W\} I(Ii)={1,...,H}×{1,...,W}，即所有像素位置的集合。深度图 D i D_i Di 将每个像素 y ∈ I ( I i ) \mathbf{y}\in\mathcal{I}(I_i) y∈I(Ii) 映射到从第 i i i 个相机观测到的深度值 D i ( y ) ∈ R + D_i(\mathbf{y})\in\mathbb{R}^+ Di(y)∈R+。同理，点图 P i P_i Pi 把每个像素映射到其对应的三维场景点 P i ( y ) ∈ R 3 P_i(\mathbf{y})\in\mathbb{R}^3 Pi(y)∈R3。重要的是，类似DUSt3R[87]，点图具有视角不变性：三维点 P i ( y ) P_i(\mathbf{y}) Pi(y) 定义在第一台相机 g 1 \mathbf{g}_1 g1 的坐标系中，我们将其视为世界参考系。

深度图 D i D_i Di：

对每个像素 ( u , v ) (u,v) (u,v)，网络输出一个正实数 D i ( u , v ) D_i(u,v) Di(u,v)；这个数表示：从第 i i i 台相机光心出发，沿着该像素对应的视线方向，到达场景表面点的距离（以米计）。 🧠 换句话说： D i D_i Di 是"从相机到场景的距离图"，一张图上每个像素都有一个深度值。
点图 P i P_i Pi：

对每个像素 ( u , v ) (u,v) (u,v)，不仅输出一个深度值 D i ( u , v ) D_i(u,v) Di(u,v)，还可以进一步计算出： P i ( u , v ) = 相机坐标系下的 3 D 点坐标 ( X , Y , Z ) P_i(u,v) = 相机坐标系下的3D点坐标 (X,Y,Z) Pi(u,v)=相机坐标系下的3D点坐标(X,Y,Z)。所以，点图是一个"每个像素都对应一个3D坐标"的映射。
视角不变性：

在传统多视图重建里，每个相机都有自己的坐标系；但为了让不同相机预测的点云能对齐在同一个空间中，VGGT 规定：所有相机看到的3D点，都转换到第1台相机的坐标系下。

最后，在关键点跟踪方面 ，我们遵循 track-any-point 方法[15,39]。具体而言，给定查询图像 I q I_q Iq 中的一个固定查询点 y q \mathbf{y}_q yq，网络输出其轨迹 T ⋆ ( y q ) = ( y i ) i = 1 N \mathcal{T}^\star(\mathbf{y}_q)=(\mathbf{y}i){i=1}^N T⋆(yq)=(yi)i=1N，其中 y i ∈ R 2 \mathbf{y}_i\in\mathbb{R}^2 yi∈R2 是该点在所有图像 I i I_i Ii 中的对应二维位置。

🧩 一、什么是"关键点轨迹"（trajectory）

假设你拍了一个场景的多张照片：

图1：一个红苹果在左下角；

图2：相机稍微移动，苹果出现在中间；

图3：相机再移动，苹果出现在右上角。

👉 如果你在第一张图上选中苹果表面一个具体像素点（比如苹果中心），我们就想问："这个点在后面的所有图像中，对应的像素在哪里？" 这条"同一个真实3D点在所有图像中的2D位置变化轨迹"，就叫作它的轨迹（trajectory）。
🧭 二、数学定义解释

意思是：我在查询图像 I q I_q Iq（比如第1张）中选一个像素 y q = ( u q , v q ) \mathbf{y}_q=(u_q,v_q) yq=(uq,vq)；模型输出一个长度为 N N N 的序列： T ⋆ ( y q ) = ( y 1 , y 2 , ... , y N ) \mathcal{T}^\star(\mathbf{y}_q) = (\mathbf{y}_1, \mathbf{y}_2, \ldots, \mathbf{y}_N) T⋆(yq)=(y1,y2,...,yN)

每个 y i \mathbf{y}_i yi 表示： "这个3D点在第 i i i 张图像 I i I_i Ii 上的位置"。所以这个轨迹告诉你："从第1张到第N张，那个同一个物体点的像素坐标是怎么移动的。"

注意，上述Transformer , f ,f ,f并不直接输出轨迹，而是输出用于跟踪的特征 T i ∈ R C × H × W T_i\in\mathbb{R}^{C\times H\times W} Ti∈RC×H×W 。跟踪由一个独立模块完成（见第3.3节），其实现的函数为 T ( ( y j ) j = 1 M , ( T i ) i = 1 N ) = ( ( y ^ j , i ) i = 1 N ) j = 1 M \mathcal{T}\big((\mathbf{y}j){j=1}^M,(T_i){i=1}^N\big)=\big((\hat{\mathbf{y}}{j,i}){i=1}^N\big){j=1}^M T((yj)j=1M,(Ti)i=1N)=((y^j,i)i=1N)j=1M。该模块接收查询点 y q \mathbf{y}_q yq 与Transformer f f f 输出的稠密跟踪特征 T i T_i Ti，并据此计算轨迹。两个网络 f f f 与 T \mathcal{T} T 以端到端方式联合训练。

预测的顺序。输入序列中的图像顺序是任意的，唯独第一张图像被选作参考帧。除第一帧之外，网络架构被设计为对其余帧具有置换等变性（即更换帧的顺序不会改变相应的预测结构）。

冗余（过完备）预测 。需要注意，VGGT 预测的各个量并不全是相互独立的。例如，正如 DUSt3R[87] 所示，相机参数 g \mathbf{g} g 可以从视角不变的点图 P \mathbf{P} P 中推断出来，比如通过求解 PnP（Perspective-n-Point）问题[23,42]。此外，深度图也可以由点图与相机参数推导得到。然而，正如我们在第4.5节所示，在训练阶段要求 VGGT 显式地预测上述所有量，即便这些量之间存在封闭形式（解析）关系，仍然会带来显著的性能提升。同时，在推理阶段我们观察到：将独立估计的深度图与相机参数进行组合，得到的三维点比直接使用专门的点图分支更准确。

3.2 特征骨干

遵循近期的三维深度学习工作[36,87,90]，我们设计了一个三维归纳偏置极少的简单架构，让模型从大量带三维标注的数据中自我学习。具体而言，我们将模型 f f f 实现为一个大型 Transformer[79]。为此，每张输入图像 I I I 首先通过 DINO[53] 被切块并标记化为 K K K 个 token，记作 t I ∈ R K × C \text{t}^I\in\mathbb{R}^{K\times C} tI∈RK×C 。将所有帧的图像 token 合并（即 t I = ∪ i = 1 N { t i I } \text{t}^I=\cup_{i=1}^N\{\text{t}^I_i\} tI=∪i=1N{tiI} ）后，送入主干网络，在逐帧自注意力层与全局自注意力层之间交替处理。

1) "极少三维归纳偏置"的简单架构，靠大数据自学3D

传统 3D 网络常内置很多几何先验（体素网格、射线采样、投影/反投影算子等）。

这里尽量不写死几何规则，而是采用通用的 Transformer，把"3D 常识"留给数据和训练去学（引用 36/87/90 的近作思路）。

好处：通用性强、可端到端训练、跨任务迁移好；坏处：需要大量带 3D 标注的数据支撑。

2) 输入图像 → DINO 切块标记化（Tokens）

每张输入图像 I ∈ R 3 × H × W I∈\mathbb{R}^{3×H×W} I∈R3×H×W 先通过 DINO（一种强大的自监督视觉骨干）做切块（patching）并标记化（tokenization）： t I ∈ R K × C \text{t}^I\in\mathbb{R}^{K\times C} tI∈RK×C

K K K：该图被切成的 patch 数（例如 14×14=196 之类）

C C C：每个 patch 的嵌入维度（如 384/768/1024）

直观理解：把每张图切成小块，每块变成一个"词向量"；所有图像的"词"放在一个大词表里，交给 Transformer 去"读懂"跨视角关系。

交替注意力（Alternating-Attention, AA） 。我们对标准Transformer做了轻微改动：引入交替注意力，使网络在逐帧与全局两个层面交替聚焦。具体来说，逐帧自注意力分别关注每一帧内的token（ t k I \text{t}^I_k tkI ），而全局自注意力则联合关注所有帧的token（ t I \text{t}^I tI）。这在跨图整合信息与对每张图像内token的激活进行归一化之间取得了平衡。默认情况下，我们使用 L = 24 L=24 L=24 层由全局与逐帧注意力交替堆叠的结构。在第4节中，我们展示了AA架构能够带来显著的性能提升。

堆叠方式 ： Global ⏟ 跨帧整合 → Per-Frame ⏟ 帧内提炼 → Global ⏟ 跨帧整合 → Per-Frame ⏟ 帧内提炼 → ⋯ × L \underbrace{\text{Global}}{\text{跨帧整合}} \rightarrow \underbrace{\text{Per-Frame}}{\text{帧内提炼}} \rightarrow \underbrace{\text{Global}}{\text{跨帧整合}} \rightarrow \underbrace{\text{Per-Frame}}{\text{帧内提炼}} \rightarrow \dots \times L 跨帧整合 Global→帧内提炼 Per-Frame→跨帧整合 Global→帧内提炼 Per-Frame→⋯×L 默认 (L=24)，即交替 24 层。

3.3 预测头

GGT 的主干（AA-Transformer）产出的 tokens，如何被"头部模块（heads）"分别解读成：相机参数、深度图、点图、跟踪特征、以及关键点轨迹。

我把它按"输入 tokens → AA-Transformer → 各个头部的输出"顺序讲清楚。

这里我们描述 f f f 如何预测相机参数、深度图、点图以及点轨迹。首先，对每个输入图像 I i I_i Ii ，我们在其对应的图像tokens t i I \text{t}^I_i tiI上附加一个相机 token t i g ∈ R 1 × C ′ \text{t}^{\mathbf{g}}_i\in\mathbb{R}^{1\times C'} tig∈R1×C′，以及四个register tokens[10] t i R ∈ R 4 × C ′ \text{t}^R_i\in\mathbb{R}^{4\times C'} tiR∈R4×C′。将 ( t i I , t i g , t i R ) i = 1 N (\text{t}^I_i,\text{t}^{\mathbf{g}}i,\text{t}^R_i){i=1}^N (tiI,tig,tiR)i=1N 串接后送入 AA-transformer，得到输出 tokens ( t ^ i I , t ^ i g , t ^ i R ) i = 1 N (\hat{\text{t}}^I_i,\hat{\text{t}}^{\mathbf{g}}i,\hat{\text{t}}^R_i){i=1}^N (t^iI,t^ig,t^iR)i=1N。

寄存器 register tokens[10] t i R ∈ R 4 × C ′ \text{t}^R_i\in\mathbb{R}^{4\times C'} tiR∈R4×C′：可视作帮助对齐/聚合的辅助槽位（参考 DetReg、DINOv2 中常见的"register tokens"做法），训练后通常丢弃不用直接输出。

这里，第一帧的相机 token 与 register tokens（ t 1 g : = t ˉ g , t 1 R : = t ˉ R \text{t}^{\mathbf{g}}_1:=\bar{\text{t}}^{\mathbf{g}}, \text{t}^R_1:=\bar{\text{t}}^R t1g:=tˉg,t1R:=tˉR）被设置为与其余帧不同的、可学习的另一组tokens（记作 t ˉ g , t ˉ R \bar{\text{t}}^{\mathbf{g}}, \bar{\text{t}}^R tˉg,tˉR）；而其余各帧使用共享的、同样可学习的tokens（ t i g : = t ˉ ˉ g , t i R : = t ˉ ˉ R , i ∈ [ 2 , ... , N ] \text{t}^{\mathbf{g}}_i:=\bar{\bar{\text{t}}}^{\mathbf{g}}, \text{t}^R_i:=\bar{\bar{\text{t}}}^{R},i\in[2,\ldots,N] tig:=tˉˉg,tiR:=tˉˉR,i∈[2,...,N]）。这样做使模型能够区分第一帧与其他帧，并将三维预测表示在第一台相机的坐标系中。

关键小技巧：第一帧的相机/寄存器 tokens 用另一组可学习的"特殊 token 参数"（ t ˉ g , t ˉ R \bar{\text{t}}^{\mathbf{g}}, \bar{\text{t}}^R tˉg,tˉR），其它帧共享另一套（ t ˉ ˉ g , t ˉ ˉ R \bar{\bar{\text{t}}}^{\mathbf{g}},\bar{\bar{\text{t}}}^{R} tˉˉg,tˉˉR）。这样网络能识别"谁是参考帧（第1帧）"，并把所有 3D 预测都放在第一帧坐标系下。

需要注意的是，细化后的相机 token 与 register tokens 会变得与帧相关------因为我们的 AA transformer 包含逐帧自注意力层，使其能将相机/寄存器 tokens 与同一图像中的相应 tokens 进行匹配。按照常规做法，输出的 register tokens t ^ i R \hat{\text{t}}^R_i t^iR 会被丢弃，而 t ^ i I , t ^ i g \hat{\text{t}}^I_i,\hat{\text{t}}^{\mathbf{g}}_i t^iI,t^ig 用于后续预测。

🧩 1. Register tokens 是什么？

"register tokens" 最早来自 DINOv2（Caron et al., 2023, MetaAI）和 Segment

Anything (SAM) 的 transformer backbone。它们是一组额外的可学习向量（tokens），在输入 patch tokens 的时候被附加进去，用来：

帮助 Transformer 聚合全局上下文；

作为信息交汇点（information bottleneck）；

引导注意力层更稳定地收敛；

提供一个全局 summary embedding，类似于 Vision Transformer 里的 [CLS] token。

但它们自己不代表任何具体物理量（例如像素、深度或相机参数），所以最终输出时不需要它们的预测结果。

🧠 2. 在 VGGT 中，register tokens 起到什么作用？

在这篇论文的上下文中，VGGT 处理多帧图像时，每帧的 token 组成是：
( t i I , t i g , t i R ) (\text{t}^I_i,\text{t}^{\mathbf{g}}_i,\text{t}^R_i) (tiI,tig,tiR)

对应：

t i I \text{t}^I_i tiI → 图像 patch tokens（视觉内容）

t i g \text{t}^{\mathbf{g}}_i tig → 相机 token（用于相机参数预测）

t i R \text{t}^R_i tiR → 寄存器 tokens（register tokens）

这四个寄存器 token 不携带图像像素或相机的物理含义，而是：

在 Transformer 的自注意力层中，作为"中转站"或"存储槽（memory slots）"，用来吸收、整合来自本帧图像 token 的局部特征。

也就是说：

它们帮助网络在不同 token（图像 patches、相机 token）之间建立稳定的交互结构；

提供一种"额外容量（capacity）"，让网络在训练早期能更快学会"如何组织特征"；

在信息传播中起到辅助聚合 / 对齐的作用。

⚙️ 3. 为什么最后会被"丢弃"？

因为这些 register tokens：

不是要预测的目标变量；

也不携带显式语义；

仅在注意力层中帮助网络组织信息；

它们在输出时已经"完成使命"，相当于训练时的"内部节点"。

因此，输出时我们只需要：

t ^ i g \hat{\text{t}}^{\mathbf{g}}_i t^ig：携带了与相机相关的信息 → 用来预测相机内外参；-

t ^ i I \hat{\text{t}}^I_i t^iI：携带了图像视觉内容的信息 → 用来预测深度、点云和跟踪特征；-

而 t ^ i R \hat{\text{t}}^R_i t^iR：没有明确的语义对应对象，所以 "按照常规做法"直接丢弃。

坐标系。 如上所述，我们在第一台相机 g 1 \mathbf{g}_1 g1 的坐标系下预测相机、点图与深度图。因此，第一台相机的外参输出被设为单位变换：其旋转四元数 q 1 = [ 0 , 0 , 0 , 1 ] \mathbf{q}_1=[0,0,0,1] q1=[0,0,0,1] ，平移向量 t 1 = [ 0 , 0 , 0 ] \mathbf{t}_1=[0,0,0] t1=[0,0,0]。回忆一下，特殊设置的相机/寄存器 tokens（ t 1 g : = t ˉ g , t 1 R : = t ˉ R \text{t}^{\mathbf{g}}_1:=\bar{\text{t}}^{\mathbf{g}}, \text{t}^R_1:=\bar{\text{t}}^R t1g:=tˉg,t1R:=tˉR）使 transformer 能够识别第一台相机。

相机预测。 相机参数 ( g ^ i ) i = 1 N (\hat{\mathbf{g}}^i)_{i=1}^N (g^i)i=1N 由输出的相机 tokens ( t ^ i g ) i = 1 N (\hat{\text{t}}^{\mathbf{g}}i){i=1}^N (t^ig)i=1N 通过额外4层自注意力加一层线性层进行预测。这构成了相机头（camera head），用于预测相机内参与外参。

相机头（Camera Head）：由相机 token 读出内外参

输入：每帧的输出相机 token t ^ i g \hat{\text{t}}^{\mathbf{g}}_i t^ig。

结构：额外 4 层自注意力 + 线性层。

输出：每帧相机参数 g ^ i \hat{\mathbf{g}}^i g^i （内参 + 外参），第 1 帧外参固定为单位变换（只预测内参）。

相机 token 相当于"这帧的相机信息收纳器"，在 AA-Transformer 里与该帧图像 tokens 充分交互后，交给相机头做一个"专注提炼 → 线性映射"，直接变成相机内外参。

稠密预测。 输出的图像 tokens t ^ i I \hat{\text{t}}^I_i t^iI用于预测稠密输出，即深度图 D i D_i Di 、点图 P i P_i Pi 与跟踪特征 T i T_i Ti 。更具体地，先通过DPT层[57]将 t ^ i I \hat{\text{t}}^I_i t^iI 转换为稠密特征图 F i ∈ R C ′ ′ × H × W F_i\in\mathbb{R}^{C''\times H\times W} Fi∈RC′′×H×W 。随后，用一个 3 × 3 3\times3 3×3 卷积层将每个 F i F_i Fi 映射到相应的深度图 D i D_i Di 与点图 P i P_i Pi。此外，DPT头还会输出稠密跟踪特征 T i ∈ R C × H × W T_i\in\mathbb{R}^{C\times H\times W} Ti∈RC×H×W，作为跟踪头的输入。我们还为每个深度图与点图分别预测偶然不确定性[40,51]： Σ i D ∈ R + H × W \Sigma^D_i\in\mathbb{R}{+}^{H\times W} ΣiD∈R+H×W与 Σ i P ∈ R + H × W \Sigma^P_i\in\mathbb{R}{+}^{H\times W} ΣiP∈R+H×W。这些不确定性图用于损失函数（详见补充材料）；训练完成后，它们与模型对预测的置信度成反比/相关（表达模型信心）。

稠密头（Dense Heads）：由图像 tokens 读出 D i , P i , T i D_i, P_i, T_i Di,Pi,Ti

输入：每帧的输出图像 tokens t ^ i I \hat{\text{t}}^I_i t^iI。

第一步：经 DPT 层 （Dense Prediction Transformer Head）变成稠密特征图 F i ∈ R C ′ ′ × H × W F_i \in \mathbb{R}^{C''\times H\times W} Fi∈RC′′×H×W

第二步：用若干 3 × 3 3\times3 3×3 卷积在 F i F_i Fi 上分别回归：

深度图 D i ∈ R H × W D_i \in \mathbb{R}^{H\times W} Di∈RH×W

点图 P i ∈ R 3 × H × W P_i \in \mathbb{R}^{3\times H\times W} Pi∈R3×H×W（每像素 3D 坐标；统一在第 1 相机系）

跟踪特征 T i ∈ R C × H × W T_i \in \mathbb{R}^{C\times H\times W} Ti∈RC×H×W（供追踪模块用的每像素描述子）

还会额外回归像素级不确定性图：

深度不确定性 Σ i D ∈ R + H × W \Sigma^D_i \in \mathbb{R}_+^{H\times W} ΣiD∈R+H×W

点图不确定性 Σ i P ∈ R + H × W \Sigma^P_i \in \mathbb{R}_+^{H\times W} ΣiP∈R+H×W
用于训练时的不确定性加权损失（噪声大的像素权重更小）。训练后它也可视作"模型对该像素预测的信心"（不确定性大 ↔ 置信低）。

小结： t ^ i I ⇒ \hat{\text{t}}^I_i \Rightarrow t^iI⇒ DPT 变稠密 F i F_i Fi → Conv 输出 D i , P i , T i D_i, P_i, T_i Di,Pi,Ti（再加不确定性图）。
D i D_i Di：距离； P i P_i Pi：世界系下3D点； T i T_i Ti：为跨视图匹配/跟踪准备的高维特征。

跟踪。 为了实现跟踪模块 T \mathcal{T} T ，我们采用 CoTracker2 架构[39]，其输入为稠密跟踪特征 T i T_i Ti。更具体地，给定查询图像 I q I_q Iq 中的一个查询点 y j \mathbf{y}j yj（训练时我们总令 q = 1 q=1 q=1 ，但任意图像都可作为查询图），跟踪头 T \mathcal{T} T 预测如下二维点集合： T ( ( y j ) j = 1 M , ( T i ) i = 1 N ) = ( ( y ^ j , i ) i = 1 N ) j = 1 M . \mathcal{T}\big((\mathbf{y}j){j=1}^M,(T_i){i=1}^N\big)=\big((\hat{\mathbf{y}}{j,i}){i=1}^N\big)_{j=1}^M. T((yj)j=1M,(Ti)i=1N)=((y^j,i)i=1N)j=1M.即在所有 I i I_i Ii 中与该查询点对应同一三维点的二维位置集合。具体做法是：首先在查询图像的特征图 T q T_q Tq 上，对查询点 y j \mathbf{y}_j yj 进行双线性采样以获得其特征向量。随后，将该特征与所有其他帧的特征图 T i T_i Ti （ i ≠ q i\neq q i=q）进行相关性计算，得到一组相关性图。这些相关性图再经由自注意力层处理，预测得到最终的二维点 y ^ i \hat{\mathbf{y}}_i y^i，它们都与查询点 y j \mathbf{y}_j yj一一对应。需要注意的是，类似 VGGSfM[83]，我们的跟踪器不假设时间顺序，因此可应用于任意图像集合，不仅仅是视频序列。

跟踪头（Tracking Head (\mathcal{T})）：由 (T_i) 找"同一 3D 点"的 2D 轨迹

采用 CoTracker2 风格的架构。

输入：所有帧的稠密跟踪特征 T i T_i Ti。给定一个查询图像 I q I_q Iq 中的查询点 y j \mathbf{y}_j yj（训练时常取 q = 1 q=1 q=1，但任何帧都可以是查询帧）。

目标：输出该点在所有帧的对应位置 ( y ^ j , i ) i = 1 N \big(\hat{\mathbf{y}}{j,i}\big){i=1}^N (y^j,i)i=1N 即"同一个 3D 点在各帧的 2D 像素坐标"。

内部做法（简化）：

在查询图 I q I_q Iq 的特征图 T q T_q Tq 上，对点 y j \mathbf{y}_j yj 做双线性采样 → 得到它的特征向量（更精确地取到子像素位置的特征）。

拿这个向量与其他帧的特征图 T i ( i ≠ q ) T_i (i\neq q) Ti(i=q)做相关性（correlation/similarity） → 得到每帧的"相关性热力图"。

把这些相关性图送入自注意力块（跨帧/跨空间地聚合证据），输出每帧的最终 2D 位置 y ^ j , i \hat{\mathbf{y}}_{j,i} y^j,i。

重要性质：不假设时间顺序 （像 VGGSfM 一样），因此它能在任意图像集合上工作，而不仅仅是视频帧。

4. 实验

本节在多项任务上将我们的方法与 最先进（SOTA） 方法进行对比，以证明其有效性。关于架构、训练损失与数据集的详细讨论见补充材料。

4.1 相机位姿估计

我们首先在 CO3Dv2[58] 与 RealEstate10K[109] 数据集上评测相机位姿估计，结果见表1。遵循[82]的设置，每个场景随机选取10张图像，并使用标准指标 AUC@30 进行评估。该指标结合了 RRA 与 RTA。RRA（相对旋转准确率）与RTA（相对平移准确率）分别对每对图像的旋转与平移的相对角误差进行计算。随后对这些角误差施加阈值以得到准确率得分。AUC是指在不同阈值下，取 RRA 与 RTA 的较小者所形成的准确率---阈值曲线下的面积。表1中的可学习方法都在 Co3Dv2 上训练过，但没有在 RealEstate10K 上训练过。我们的前馈式模型在两个数据集与全部指标上稳定优于竞争方法，甚至超过那些需要昂贵后处理的算法（如 DUSt3R/MASt3R 的全局对齐、VGGSfM 的束调整），这些后处理通常耗时超过10秒。相比之下，VGGT在同一硬件上仅以前馈方式即可取得更优性能，耗时仅0.2秒。相较同期工作[73,85,96,105]（以 ‡ 标示），我们的方法在性能上具有显著优势，速度则与最快变体 Fast3R[96] 相当。此外，在RealEstate10K上（表1中各方法均未在其上训练），我们的性能优势更为显著。这验证了 VGGT 的更强泛化能力。

表1。在 RealEstate10K[109] 与 CO3Dv2[58] 上进行相机位姿估计（每个场景随机10帧）。所有指标越高越好。运行时间在一张 H100 GPU上测得。各方法均未在 Re10K 上训练；括号 () 表示未在 CO3D 上训练。带 ‡ 的方法表示同期工作。

我们的结果还表明，将 VGGT 与视觉几何优化中的 束调整（BA） 等方法结合，仍可进一步提升性能。具体而言，用 BA 对预测的相机位姿与轨迹进行细化，可进一步提升准确率。需要注意，我们的方法直接预测出接近准确的点/深度图，可作为 BA 的良好初始化。这就省去了[83] 中 BA 所需的三角化与多次迭代细化，因而我们的方案即使加上 BA 也仅需约2秒，速度显著更快。因此，尽管 VGGT 的前馈模式已优于此前的所有替代方法（不论其是否前馈），但后优化仍能带来收益，说明仍有改进空间。

4.2 多视图深度估计

参照 MASt3R[43] 的设定，我们在 DTU[35] 数据集上进一步评估多视图深度估计结果。我们报告 DTU 的标准指标，包括 Accuracy（预测到真值的最小欧氏距离）、Completeness（真值到预测的最小欧氏距离）以及它们的平均 Overall（即 Chamfer 距离）。在表2中，DUSt3R 与我们的 VGGT 是唯二在未知相机真值条件下运行的方法。MASt3R 利用相机真值对匹配点进行三角化以得到深度图。与此同时，诸如 GeoMVS-Net 的深度多视图立体方法使用相机真值来构建代价体。

表2。 DTU[35] 数据集上的稠密 MVS 估计。表格上半部分为已知真值相机的算法，下半部分为未知真值相机的算法。

我们的方法显著优于 DUSt3R，将 Overall 从 1.741 降至 0.382。更重要的是，它的结果与测试时已知相机真值的方法相当。这一显著提升很可能归因于我们的多图像训练机制：模型原生学会多视图三角化推理，而不是依赖临时的对齐流程；例如 DUSt3R 只是对多对相机的两两三角化进行平均。

4.3 点图估计

我们还在 ETH3D[65] 数据集上，将预测点云的精度与 DUSt3R 和 MASt3R 进行比较。每个场景我们随机采样10帧。预测点云通过 Umeyama[77] 算法与真值对齐。在使用官方掩膜过滤无效点之后，我们报告结果。对于点图估计，我们同样报告 Accuracy、Completeness 与 Overall（Chamfer 距离）。如表3所示，尽管 DUSt3R/MASt3R 进行了昂贵的优化（全局对齐，约每个场景10秒），我们的前馈式方法每次重建仅需0.2秒，却仍显著超越它们。

表3。 ETH3D[65] 上的点图估计。DUSt3R 与 MASt3R 使用全局对齐，而我们的方法是前馈式，因此更快。其中 Ours (Point) 表示直接使用点图头的结果；Ours (Depth + Cam) 表示由深度图头与相机头组合构建点云的结果。

同时，与直接使用点图头相比，我们发现使用深度头+相机头的预测（即用预测相机参数把预测深度图反投影到3D）精度更高。我们认为，这得益于把复杂任务（点图估计）分解为更简单的子问题（深度与相机预测）------尽管在训练中相机、深度与点图是联合监督的。

在图3中，我们给出了在真实场景下与 DUSt3R 的定性对比；更多示例见补充材料。VGGT 输出高质量预测并具备良好泛化，在域外挑战（如油画、无重叠帧、以及重复/同质纹理如沙漠的场景）上表现出色。

图3。在真实复杂场景中，将我们预测的三维点与 DUSt3R 进行对比。如第一行所示，我们的方法成功预测出一幅油画的几何结构，而 DUSt3R 给出的是略有畸变的平面。在第二行中，我们的方法能从两张毫无重叠的图像中正确恢复三维场景，而 DUSt3R 失败。第三行给出一个具有重复纹理的挑战案例，我们的预测依然高质量。由于 DUSt3R 在超过32帧时会内存耗尽，因此这里不包含超过32帧的示例。

4.4 图像匹配

双视图图像匹配是计算机视觉中被广泛研究的课题[47,61,69]。它可视为刚体点跟踪的一个特例，只涉及两个视图；因此，即便我们的模型并非专为此任务设计，它仍是评测跟踪精度的合适基准。我们遵循 ScanNet 数据集[9]上的标准评测流程[21,61]，结果见表4。对每对图像，我们提取匹配点并用其估计本质矩阵，随后分解得到相对相机位姿。最终指标为相对位姿准确率，用 AUC 度量。在评测时，我们采用 ALIKED[107] 检测关键点，并将其视作查询点 y q y_q yq。随后将这些点输入我们的跟踪分支 T \mathcal{T} T，在第二帧中寻找对应点。评测中的超参数（如匹配数量、RANSAC 阈值）与 Roma[21] 一致。尽管未针对双视图匹配进行显式训练，表4显示 VGGT 仍取得了最高准确率。

4.5 消融实验

特征骨干。

我们首先通过与两个替代注意力架构对比来验证所提 交替注意力（AA） 设计的有效性：(a)仅全局自注意力；(b)交叉注意力。为保证公平性，所有变体参数量相同，并均使用总计 2 L 2L 2L 层注意力层。在交叉注意力变体中，每一帧都会独立关注所有其他帧的tokens，虽能最大化跨帧信息融合，但会显著增加运行时间，尤其在输入帧数增多时。其他超参数（如隐藏维度、注意力头数）保持一致。我们选用点图估计精度作为消融评测指标，因为它能反映模型对场景几何与相机参数的联合理解。表5结果显示，我们的 AA 架构相较两种基线有明显优势。此外，我们的多项初步探索实验一致表明，采用交叉注意力的架构通常不及仅使用自注意力的架构。

多任务学习。

我们也验证了单一网络同时学习多种三维量的好处，尽管这些输出可能相互重叠（例如深度图+相机参数即可生成点图）。如表6所示，若训练时去掉相机、深度或轨迹中的任一任务，点图估计精度都会明显下降。值得注意的是，加入相机参数估计能显著提升点图精度，而加入深度估计只带来边际改进。

4.6 下游任务的微调

我们现在展示：VGGT 的预训练特征提取器可以在下游任务中复用。

前馈式新视角合成

前馈式新视角合成发展迅速[4,31,34,36,70,84,95,104]。大多数现有方法以相机参数已知的图像为输入，预测新视角对应的目标图像。我们不依赖显式3D表示，而是遵循 LVSM[36]，对 VGGT 做出修改，使其直接输出目标图像。但我们不假设输入帧的相机参数已知。

我们严格遵循 LVSM 的训练与评测流程，例如使用4个输入视图，并采用Plücker射线来表示目标视角。我们对 VGGT 做了一个简单改动。与之前相同，输入图像先由 DINO 转为tokens。随后，对目标视图，我们使用一个卷积层将其Plücker射线图像编码为tokens。表示输入图像与目标视图的这些tokens被拼接后，送入AA transformer处理。之后，由DPT头回归目标视图的RGB颜色。需要强调：我们不向源图像输入Plücker射线；因此模型并未获得这些输入帧的相机参数。

LVSM 在 Objaverse 数据集[11]上训练；我们使用一个体量约为其20%的相似内部数据集。训练与评测的更多细节见文献[36]。如表7所示，尽管我们不需要输入相机参数且训练数据少于 LVSM，在 GSO 数据集[17]上仍取得了具有竞争力的结果。我们预期：若使用更大规模训练集，结果还会进一步提升。图4展示了定性样例。

动态点跟踪

动态点跟踪近年成为竞争激烈的任务[15,32,39,93]，也是我们学习特征的另一项下游应用。按照标准做法，我们报告以下点跟踪指标：遮挡准确率（OA）------遮挡预测的二分类准确率； δ vis avg \delta^{\text{avg}}_{\text{vis}} δvisavg------在给定像素阈值内可见点被准确跟踪的平均比例；以及平均Jaccard（AJ）------同时衡量跟踪与遮挡预测准确性。

我们对 CoTracker2[39]（SOTA）进行适配：用我们的预训练特征骨干替换其骨干网络。此举是必要的，因为 VGGT 在训练时使用的是无序图像集合，而非时序动态视频。我们的骨干预测跟踪特征 T i T_i Ti，它替换原特征提取器的输出，随后输入 CoTracker2 的其余结构，最终预测轨迹。我们在 Kubric[29] 上对该改造后的跟踪器进行端到端微调。如表8所示，整合预训练VGGT后，CoTracker 在 TAP-Vid 基准[13]上的性能显著提升。例如，在 TAP-Vid RGB-S 数据集上，使用 VGGT 的跟踪特征可将 δ vis avg \delta^{\text{avg}}_{\text{vis}} δvisavg从 78.9 提升到 84.0。尽管 TAP-Vid 包含快速动态运动的视频，我们的方法仍有强劲表现，表明其特征具有良好的泛化能力。

5. 结论

我们提出Visual Geometry Grounded Transformer（VGGT），这是一种前馈式神经网络，能够直接从上百张输入视图中估计所有关键的三维场景属性。它在多项三维任务上取得了最先进（SOTA）的结果，包括相机参数估计、多视图深度估计、稠密点云重建以及三维点跟踪。我们提出的简洁、以神经网络为先的方法，有别于传统的视觉几何方法------后者通常依赖后期优化来获得准确且面向特定任务的结果。我们方法的简单性与高效率使其非常适合实时应用；这也是相较于基于优化的方法的另一项优势。