论文来源 :Dual Inequalities for Stabilized Column Generation Revisited
作者:Timo Gschwind 和 Stefan Irnich
这篇文献《Dual Inequalities for Stabilized Column Generation Revisited》提出了一种新的方法来加速列生成(Column Generation,CG)的过程,主要通过使用对偶不等式(Dual Inequalities,DIs)来稳定对偶变量,从而提高CG的收敛速度并减少尾效应。文中不仅扩展了之前的方法,还通过引入新的矩阵性质来识别新的深对偶最优不等式(DDOIs)和对偶最优不等式(DOIs),并将其应用于切割库存(Cutting Stock,CS)、二进制装箱(Bin Packing,BP)、图着色(Vertex Coloring,VC)等问题。
一、为什么需要"稳定"的列生成?
传统 CG 在求解大型 LP 时,经常遇到两类痛点:
- 对偶震荡:对偶变量在迭代中大幅震荡;
- 退化尾效应 :主问题(多为集合覆盖/划分)高度退化,导致改进极慢。
本文的核心思想,是在对偶空间 中加入有效不等式(DIs),把"好"的对偶区域"框"出来,从而让 CG 更稳、更快。
二、作者的五项主要贡献
- 等价性定理的推广(命题 1) :明确了原始模型 P P P 和扩展模型 P ~ \tilde{P} P~ 在深度对偶最优不等式(DDOIs)成立时的等价条件(同最优值/可转化最优解等,见第 2 节)。这给"加哪些不等式才不损失最优性"提供了判据。
- 新的矩阵性质 → 新类不等式 :提出交换性质 、覆盖性质 、行替换性质 等,进而得到加权子集不等式(WSIs) 、对子不等式(pair inequalities)等一系列 DOI/DDOI(第 3 节)。
- 应用范围更广 :除切割库存(CS)与装箱(BP)外,进一步覆盖向量装箱(VP) 、图着色(VC) 、带冲突装箱(BPC)(第 3 节)。
- 过度稳定化 + 可恢复 :即使加入的 DI 并非 DDOIs、导致原问题主解不可行,作者给出恢复算法,把扩展模型的解在不增成本的前提下拉回 原始模型 的可行解(第 4.2 节,含示例与算法 1)。
- 动态分离(separation) :不一次性塞入大量 DI,而是在 CG 过程中动态识别并加入被违反的 DI,在稳定性与 RMP 规模间取得更优平衡(第 4.1 节)。
三、核心概念与关键定理
1)DI/DOI/DDOI
- DI :在对偶变量 π \pi π 上的任何有效不等式 E ⊤ π ≤ e E^\top \pi \le e E⊤π≤e。
- DOI :所有对偶最优解都满足的 DI。
- DDOI :至少有一个对偶最优解满足的一组 DI。
- 命题 1 :令 D D D 和 D ~ \tilde{D} D~ 分别是原始模型和扩展模型的对偶模型。若 E ⊤ π ≤ e E^\top \pi \le e E⊤π≤e 是 DDOIs ,则 ( P , D ) (P,D) (P,D) 与 ( P ~ , D ~ ) (\tilde P,\tilde D) (P~,D~)等价 (最优值相同, P ~ \tilde{P} P~ 的最优解可转回 P P P 等)。这为"加不加、怎么加"提供了理论支持。
2)交换性质 → 加权子集不等式(WSIs)
- 交换性质:若列向量允许用某些行的系数替换另一些行的系数,则可推出对偶上的比较式。
- 定理 1 :在 CS/VP 中,如果"一个大件 能被若干小件 (可带倍数)装进去"(一维: w h ≥ ∑ s ∈ S t s w s w_h \ge \sum_{s\in S} t_s w_s wh≥∑s∈Stsws;高维对各维都成立),则有
π h ≥ ∑ s ∈ S t s π s , \pi_h \ge \sum_{s\in S} t_s\pi_s, πh≥s∈S∑tsπs,
这就是 WSI (子集不等式的加权版,子集不等式是其特例)。直观理解:在任一切割/装箱方案中,用一件 (h) 总不比用那包"小件组合"更容易,所以对偶价应不更小。
3)行替换性质 → 对子不等式(Pair Inequalities)
- 行替换 :在二元矩阵 + 单位需求 的模型(如 BP/VC/BPC)中,若某列含 h h h 行而不含 i i i 行,能换成含 i i i 行的列,则得 π h ≥ π i \pi_h \ge \pi_i πh≥πi。
- 定理 2 :给出在 BP、VC、BPC 中对子不等式/子集不等式成为 DDOIs/DOIs 的判据(例如在 BP 中 w h ≥ w i w_h\ge w_i wh≥wi 则 π h ≥ π i \pi_h\ge\pi_i πh≥πi 至少是 DDOI;若再有 w h + w i > L w_h+w_i>L wh+wi>L 则提升为 DOI)。
4)覆盖性质 & 聚合/消元
- 覆盖 ≥ vs 划分 =:当矩阵满足"删一个元素仍可行"(遗传性),把"等式"换成"覆盖不等式"有利于对偶非负、减少震荡。
- 行聚合 与行消元 :等价保最优的聚合/消元可显著缩小 RMP 与子问题规模(例如 VC 中邻接包含关系可消元)。
四、动态分离与"可恢复"的过度稳定化
1)分离怎么做(与定价"顺带"完成)
- CS(UKP)/BP(KP) :用 DP 解子问题时,同一张 DP 图 上就能读出对每个 h h h 的"最违背"WSI/SI,几乎零额外代价 (第 4.1 节,第 10 页有 UKP 的 DP 状态图示意)。
- VC(MWIS) :对每个 h h h 在子图 G [ S h ] G[ S_h ] G[Sh] 上求一次 MWIS 即可分离(候选集 S h S_h Sh 只保"冲突不多于 h h h"的点)。
- BPC(KPC) :一般图很难;区间图上可用 DP。作者实现了三种分离:对子枚举、基于 DP 的启发式、严格 DP。
2)过度稳定化与恢复算法
- 若加入的 DI 不是 DDOIs,可能裁掉了整个对偶最优多面体 , P ~ \tilde{P} P~ 的最优主解含正的 y y y(DI 变量),不可直接还原 到 P P P。
- 示例 1给了 BP 的反例;
- 算法 1 提供了成本不变 的恢复流程 (把"DI 列 + 原列"组合,逐步把 y y y 吸收回真实列;若无法恢复,移除造成问题的 WSI 再解)。实测中恢复很少触发、迭代数极小。
五、数值实验
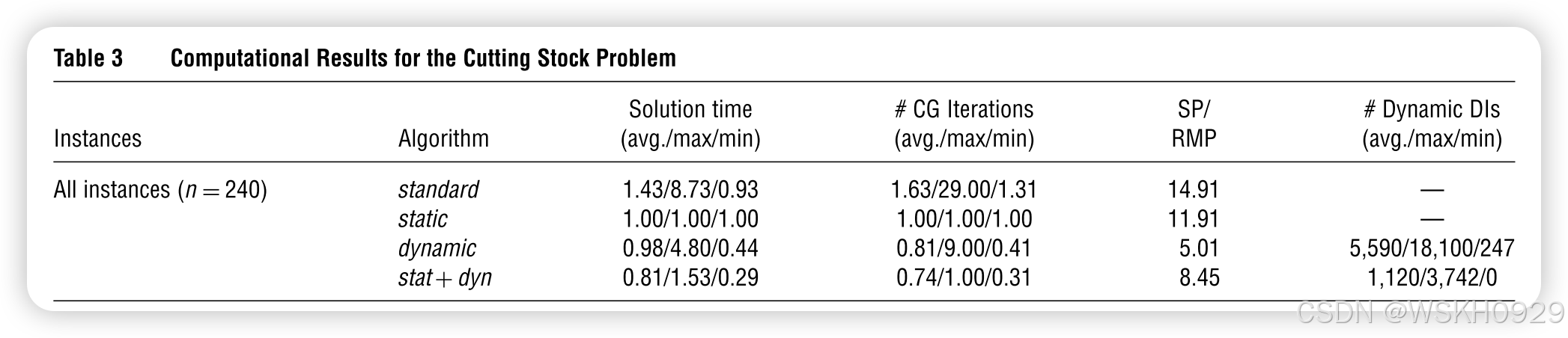
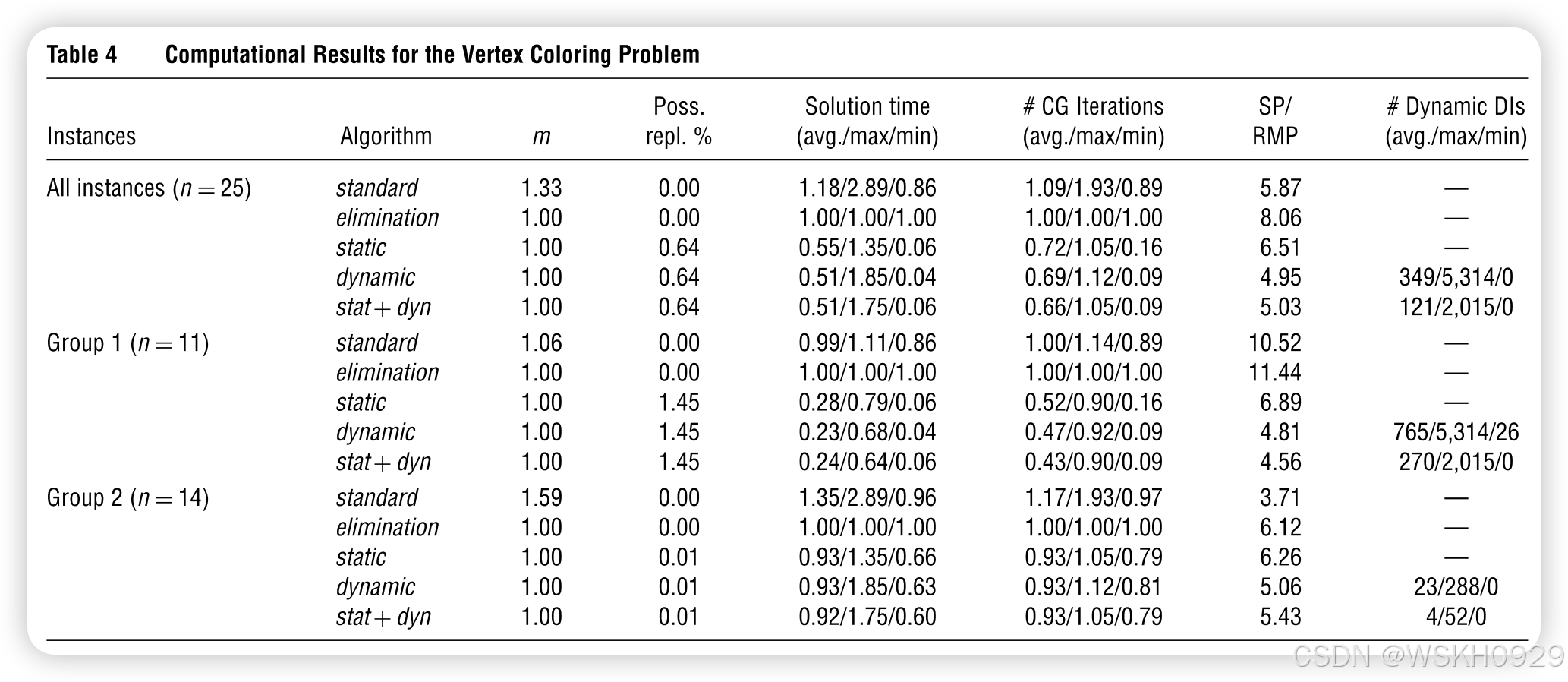
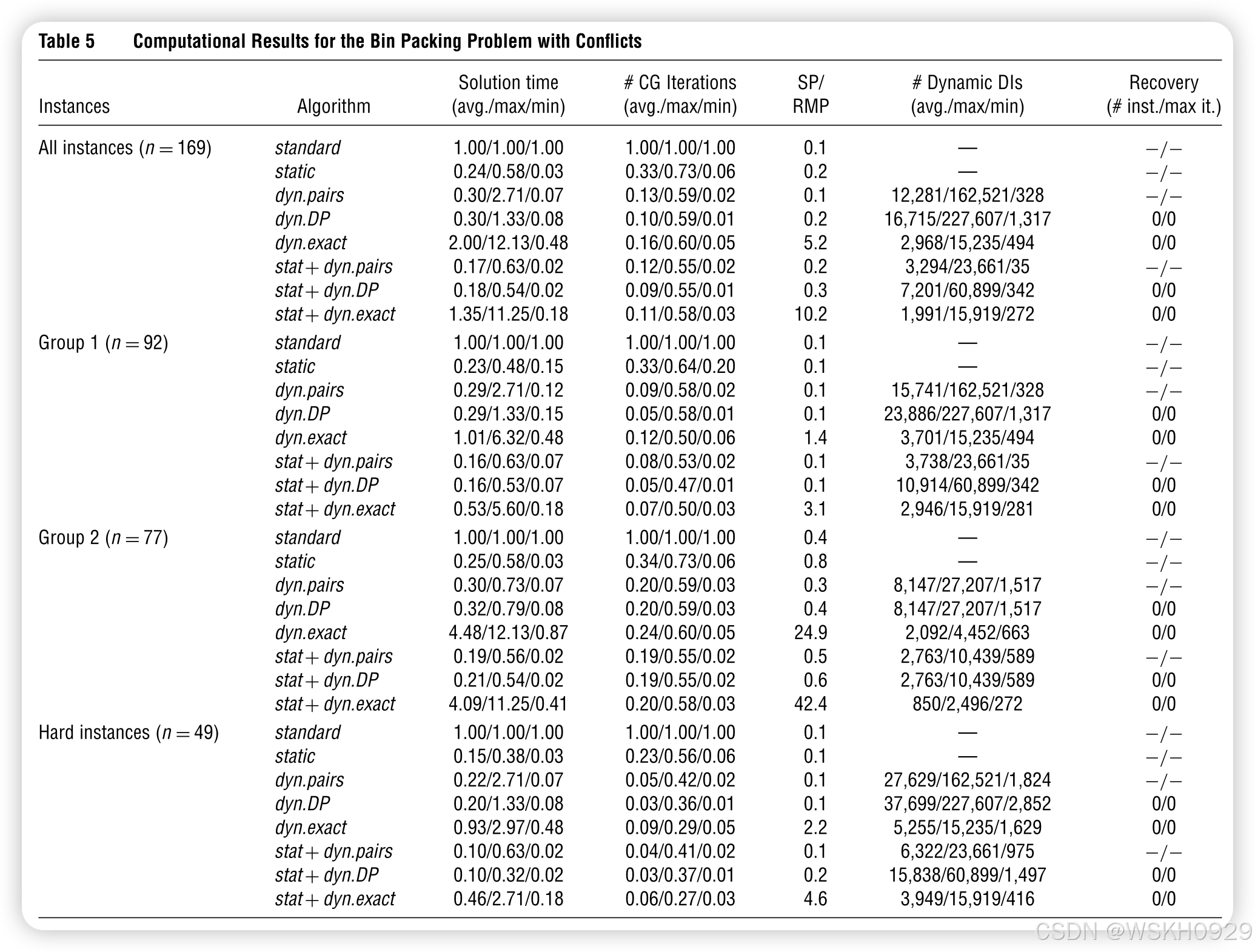
文中第 5 节给出 4 类问题的大量对比(表 2--5),时间以"相对基线"呈现,越小越好
六、结语
这篇文章把"在对偶空间 做切割"的思路系统化:用矩阵性质刻画 DOI/DDOI 的充要条件 ,给出动态分离 + 恢复 的完整算法框架,并用大量实验证明在多类经典 CG 应用上显著减少迭代、总体提速。
如果 CG 过程出现对偶震荡或尾效应,按"静态少量 + 动态分离 +(必要时)恢复 "的方式,往往能用很小的计算代价换到很可观的性能提升。更多细节(术语表、定理编号、DP 图示、实验表格)请直接翻阅原文的 表 1)、定理 1、定理 2、第 10 页(DP 图)、表 2--5。