一、算法分析
算法 + 数据结构 = 程序

1、时间复杂度
时间复杂度介绍



计算时间复杂度 - 常数阶 均为O(1)

计算时间复杂度 - 线性阶

计算时间复杂度 - 平方阶
计算时间复杂度 - 立方阶

计算时间复杂度 - 对数阶

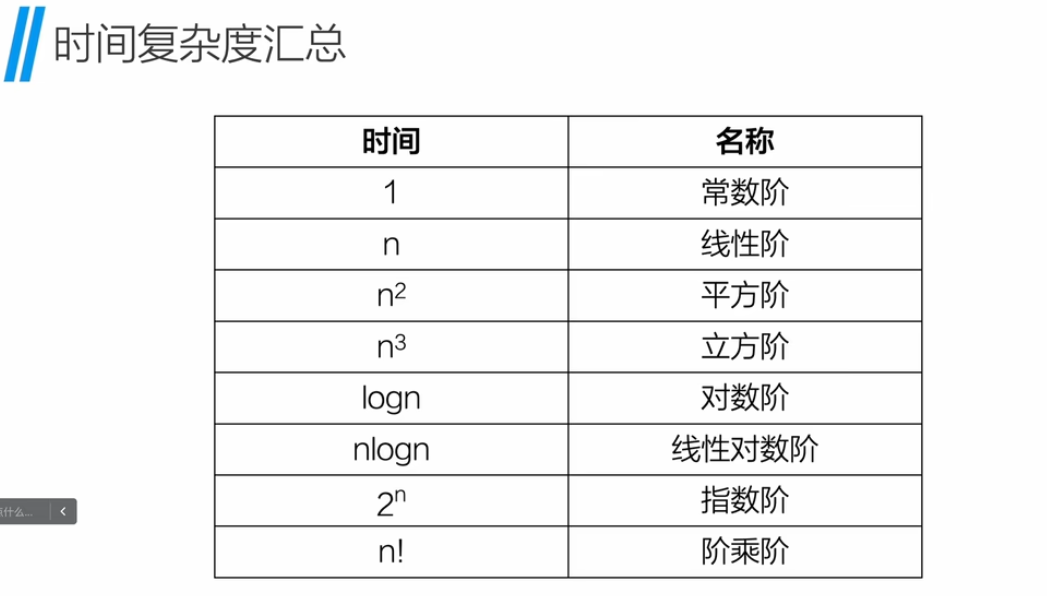
时间复杂度汇总
2、空间复杂度(了解)

3、抽象数据类型ADT(了解)


二、顺序表与链表
1、线性表的定义

2、顺序表
顺序表的创建


顺序表 - 初始化 initList(&list)
cs
#include <stdio.h>
#define MAXSIZE 100
// 将int类型改为别名ElmType
typedef int ElmType;
// 定义顺序表结构体,别名为SeqList
typedef struct
{
ElmType data[MAXSIZE]; // int类型的数组数据
int length; // 记录数据数量
}SeqList;
// 定义顺序表初始化函数
void initList(SeqList *L) //参数:传入一个SeqList类型的指针
{
L->length = 0;
}
int main(int argc,char const *argv[])
{
// 利用SqeList顺序表结构体,声明一个顺序表list
SeqList list;
// 调用函数initList,初始化顺序表list
initList(&list);
printf("初始化成功,目前长度占用%d\n", list.length);
printf("目前内存占用%zu字节\n", sizeof(list.data));
return 0;
}顺序表 - 在尾部添加元素
cs
// 定义顺序表添加元素函数
int appendElem(SeqList *L,ElmType e) //参数:传入一个SeqList类型的指针,int类型的数据e
{
// 先判断顺序表是否满了
if (L->length >= MAXSIEZE)
{
printf("顺序表已满\n");
return 0;
}
// 添加元素值为e
L->data[L->length] = e;
// 数量也要更新+1
L->length++;
return 1;
}
int main(int argc,char const *argv[])
{
appendElem(&list, 88)
return 0;
}顺序表 - 遍历

顺序表 - 插入元素 insertList(&list, i, value)
原理:在指定下标如5的位置插入数据,从5及以后下标的元素都要往后挪一个位置,再把新元素插入下标为5的位置。
cs
// 定义顺序表插入元素函数
int insertElem(SeqList *L,int pos, ElmType e) //参数:传入一个SeqList类型的指针,要插入的位置下标pos,int类型的数据e
{
if (L->length >= MAXSIZE)
{
printf("表已经满了\n")
return 0;
}
// 如果插入位置在最后面是错误的,应该在已有元素位置范围内
if (pos < 1 || pos > L->length)
{
printf("插入位置错误\n")
return 0;
}
if (pos <= L->length)
{
// 把元素从后往前依次重新赋值
for (int i = L->length-1; i >= pos-1; i--)
{
// 例如l.data[6] = l.data[5],把原来位置5的数据赋值给位置6
L->data[i+1] = L->data[i];
}
// 插入元素e
L->data[pos-1] = e;
L->length++;
}
return 1;
}
int main(int argc,char const *argv[])
{
insertElem(&list, 2, 88)
return 0;
}顺序表 - 删除元素 removeList(&list, i, &vlaue)
注:顺序结构删除元素,实际都是通过改变下标实现的,并不是真正的删除
原理:在指定下标如5的位置删除数据,从5及以后下标的元素都要往前挪一个位置,重新覆盖元 素值。
cs
// 定义顺序表删除元素函数
int deleteElem(SeqList *L,int pos, ElmType *e) //参数:传入一个SeqList类型的指针,要删除的位置下标pos,一个指针(用于返回删了哪个数据相关信息)
{
if (L->length == 0)
{
printf("空表\n")
return 0;
}
// 如果删除位置在最后面是错误的,应该在已有元素位置范围内
if (pos < 1 || pos > L->length)
{
printf("删除数据位置错误\n")
return 0;
}
// 把要删除的数据,放到指针e中
*e = L->data[pos-1];
if (pos < L->length)
{
for (int i = pos; i < L->length; i++)
{
L->data[i-1] = L->data[i];
}
}
L->length--;
return 1;
}
int main(int argc,char const *argv[])
{
ElemType delData;
deleteElem(&list, 2, &delData);
printf("被删除位置2的数据为%d\n", delData);
return 0;
}顺序表 - 查找 findList(&list, value)
原理:循环整个顺序表,直到查找到对应值,返回对应位置。
cs
// 定义顺序表查找元素函数
int findElem(SeqList *L, ElmType e) //参数:传入一个SeqList类型的指针,要查找的元素e
{
if (L->length == 0)
{
printf("空表\n")
return 0;
}
//
for (int i = 0; i < L->length; i++)
{
if (L->data[i] == e)
{
return i+1;
}
}
return 0;
}
int main(int argc,char const *argv[])
{
printf("40的数据位置为%d\n", findElem(&list, 40));
return 0;
}顺序表 - 动态分配内存地址初始化



3、链表
链表的创建

创建链表结构体
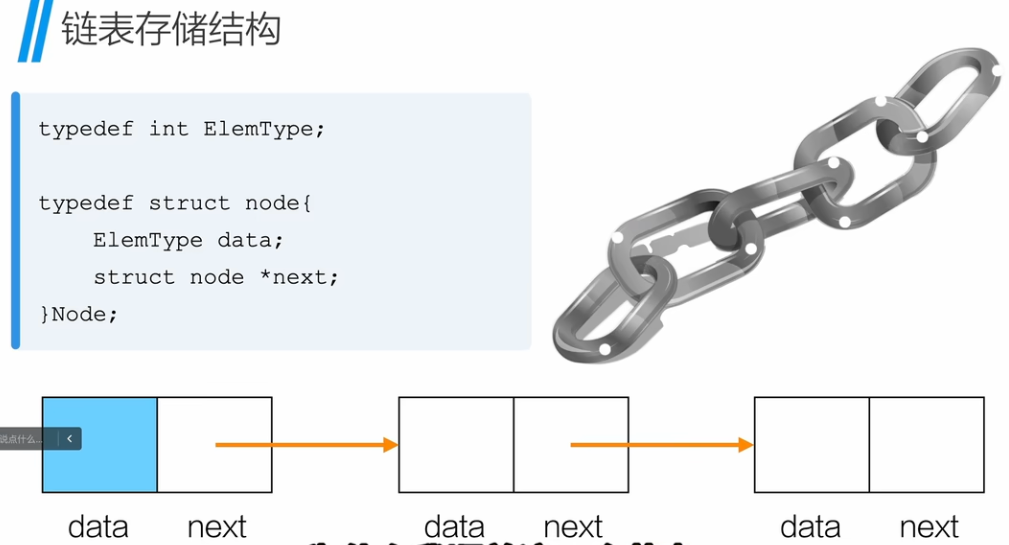
单链表 - 初始化
**已有链表结构体Node,**创建链表头指针head

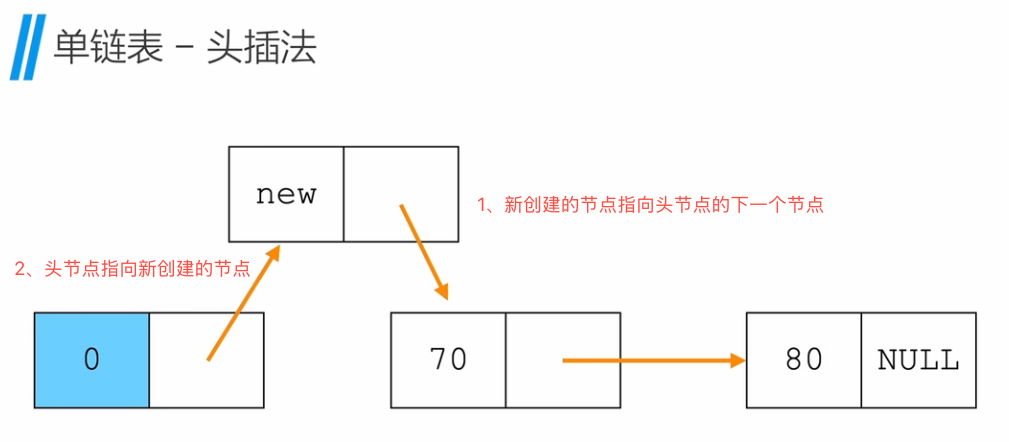
单链表 - 头插法

单链表 - 遍历

单链表 - 尾插法
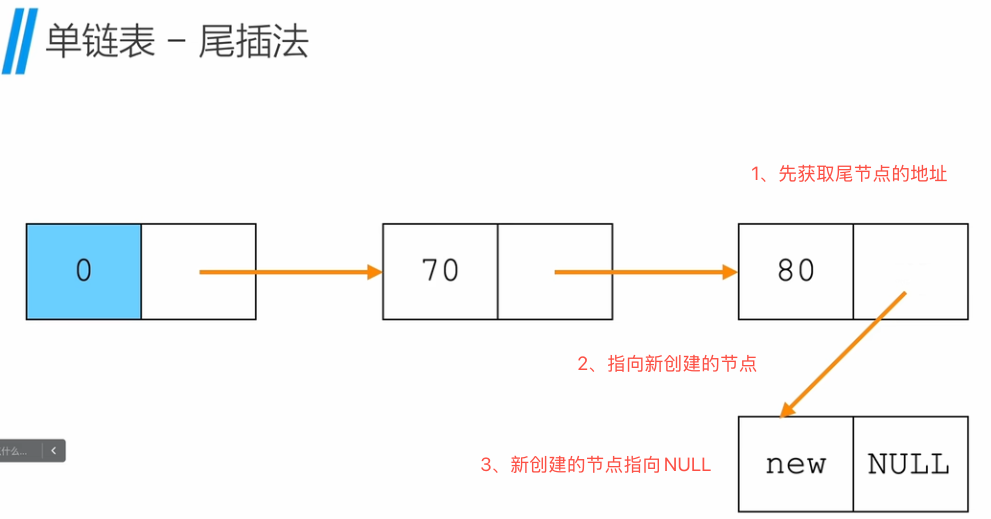



单链表 - 在指定位置插入数据
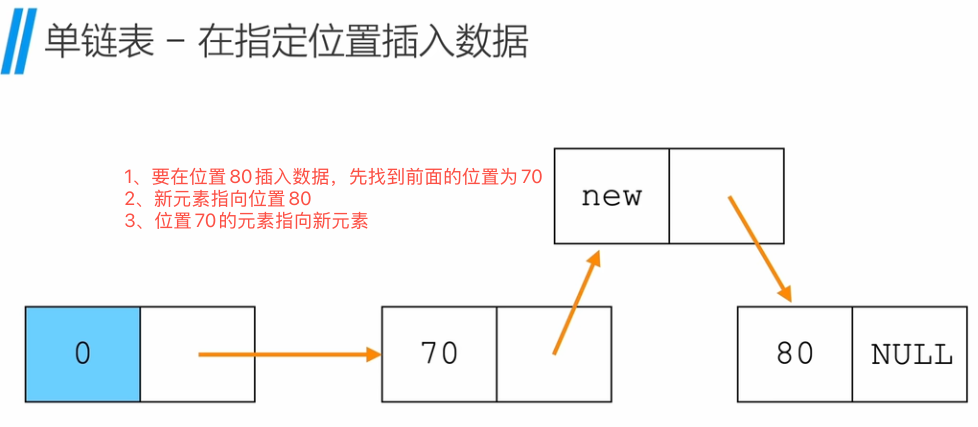


单链表 - 删除节点
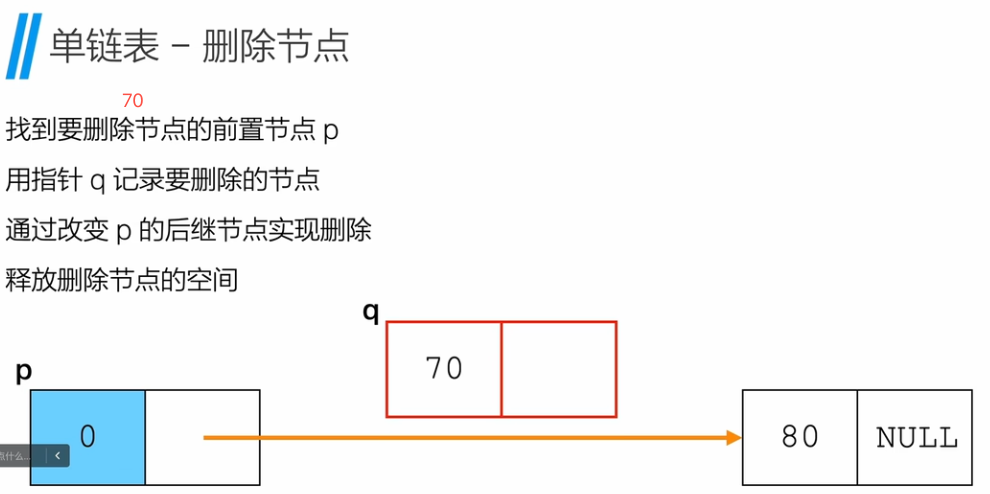


单链表 - 获取列表长度
单链表 - 释放列表




4、单向循环链表

5、双向循环链表
双向链表的创建

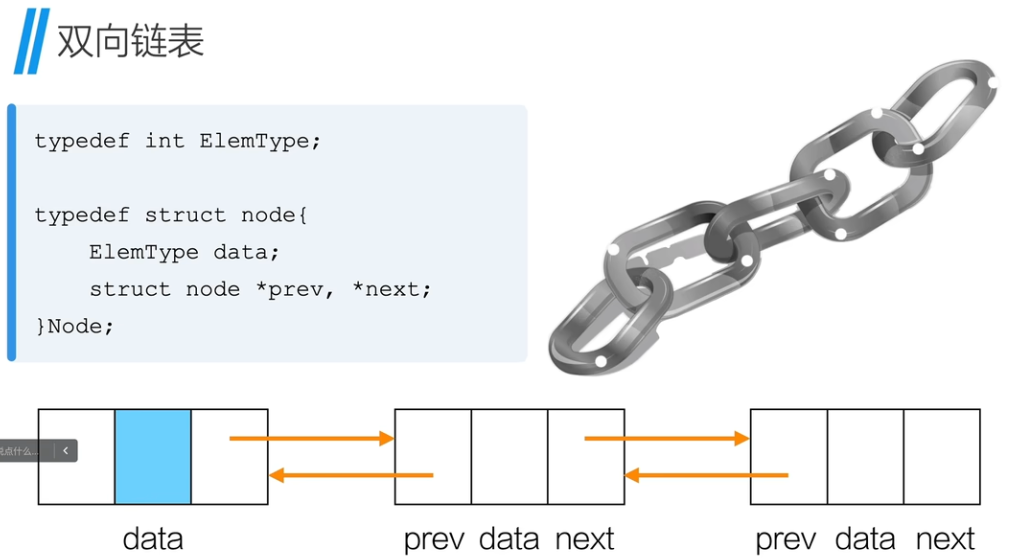
双向链表 - 初始化


双向链表 - 头插法
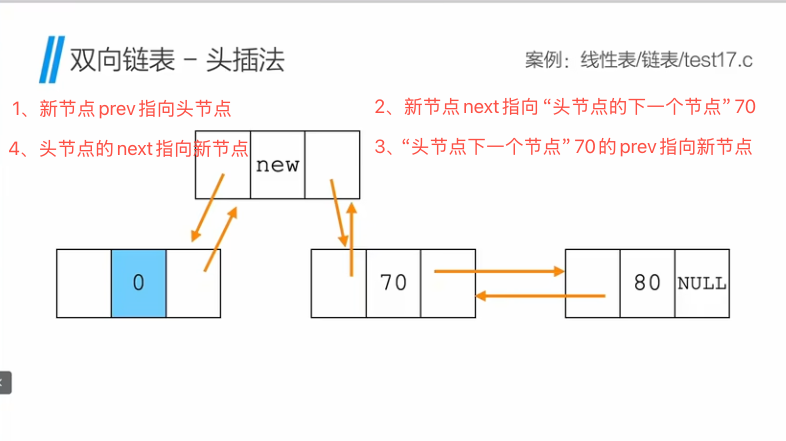

双向链表 - 尾插法
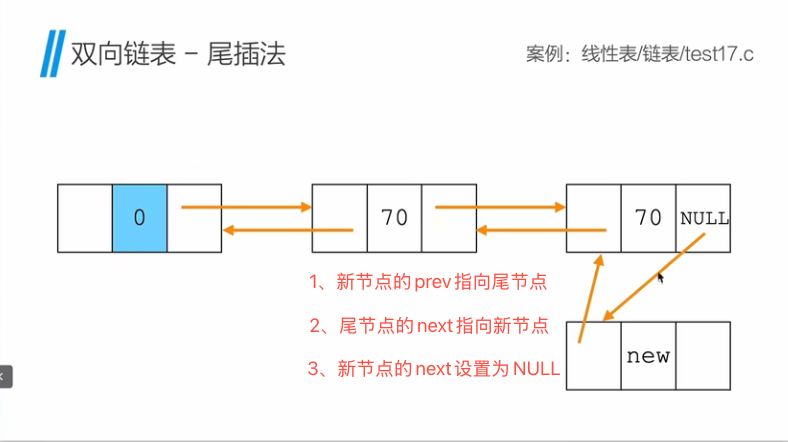

双向链表 - 在指定位置插入数据
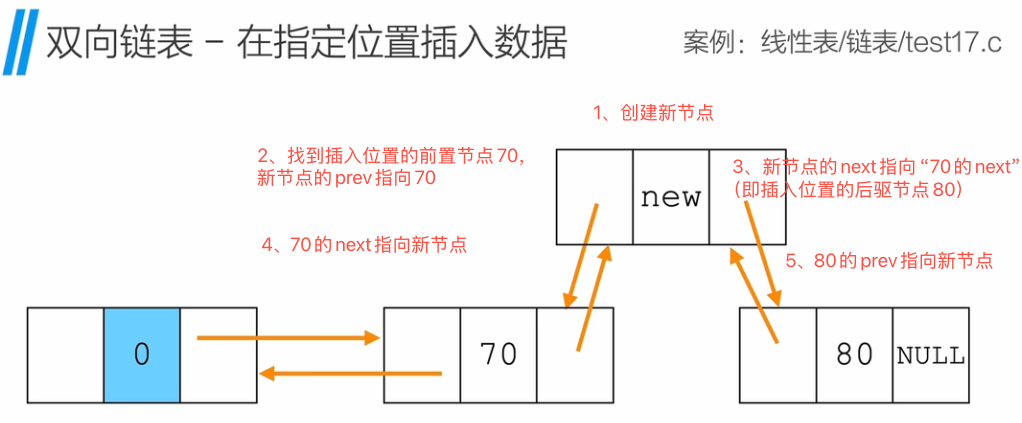


双向链表 - 删除节点


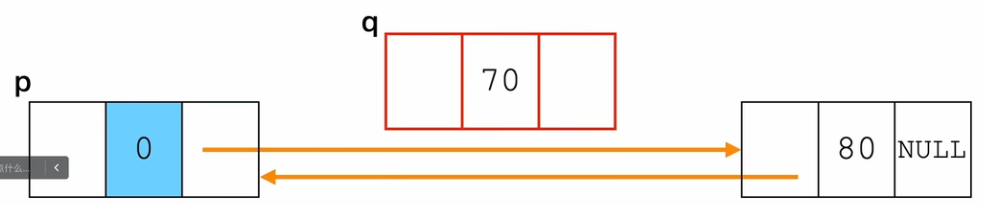



6、顺序表与链表对比
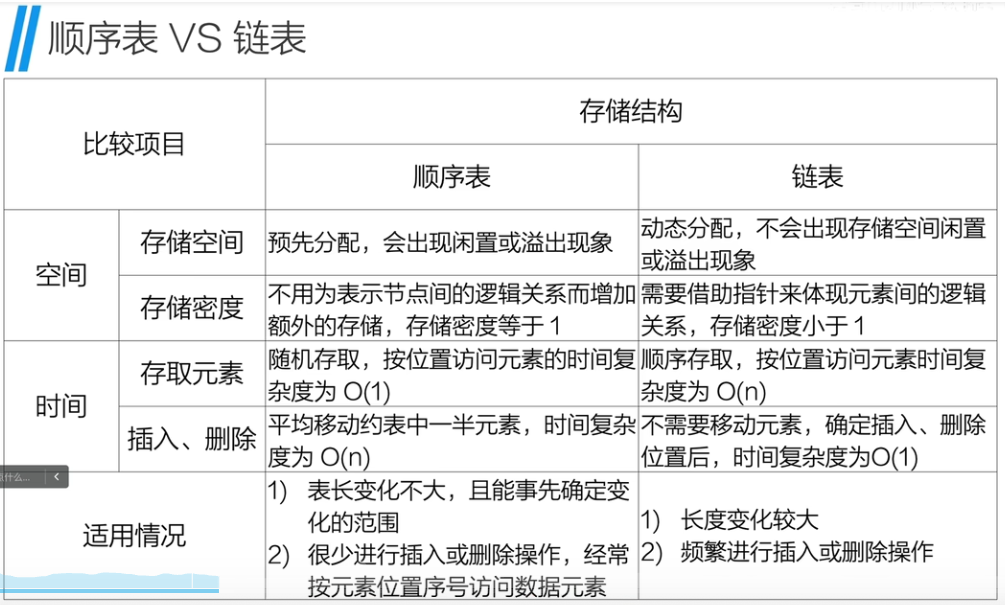
三、栈与队列
1、栈
栈的创建


栈 - 初始化

栈 - 判断是否为空

栈 - 进栈

栈 - 出栈
注:顺序结构删除元素,实际都是通过改变下标实现的,并不是真正的删除

栈 - 获取栈顶元素

汇总代码
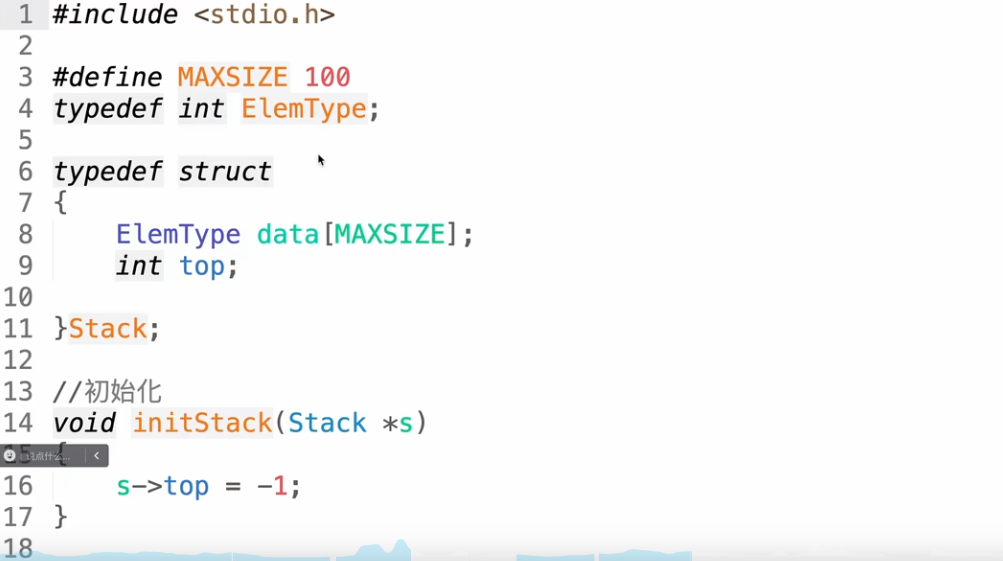




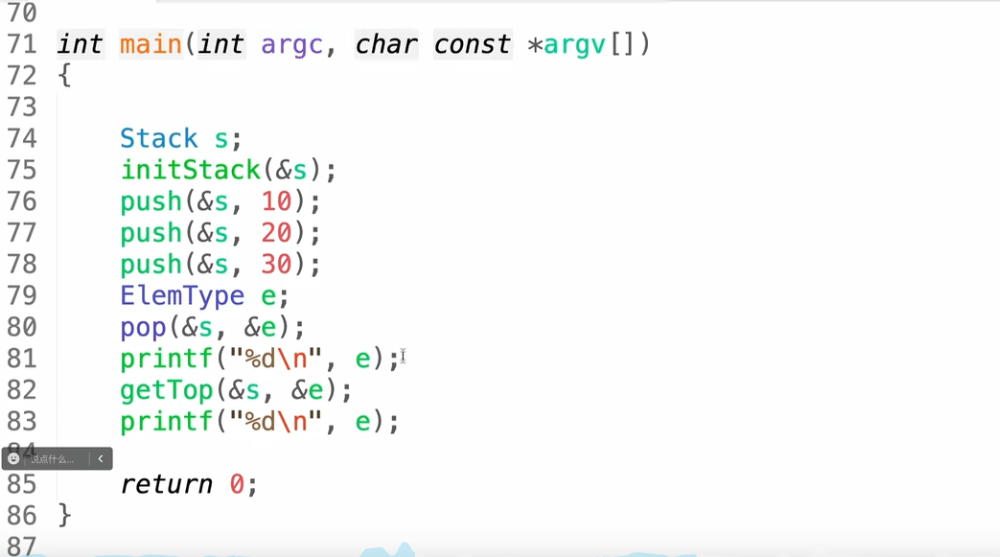
栈 - 动态内存分配
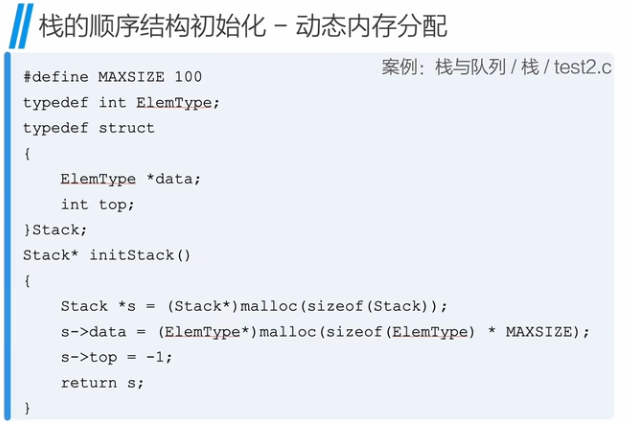
2、栈的链式结构
栈的链式结构创建
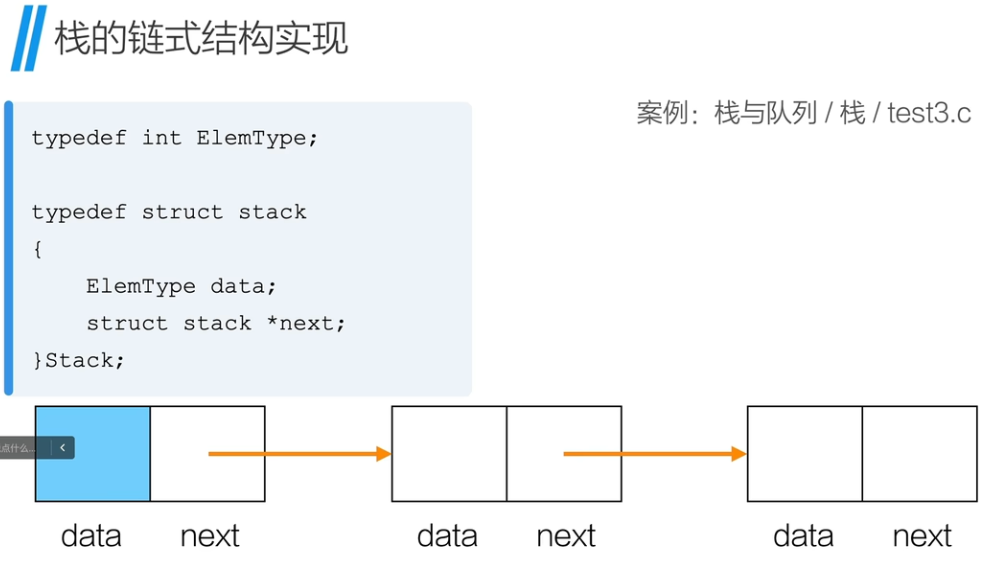
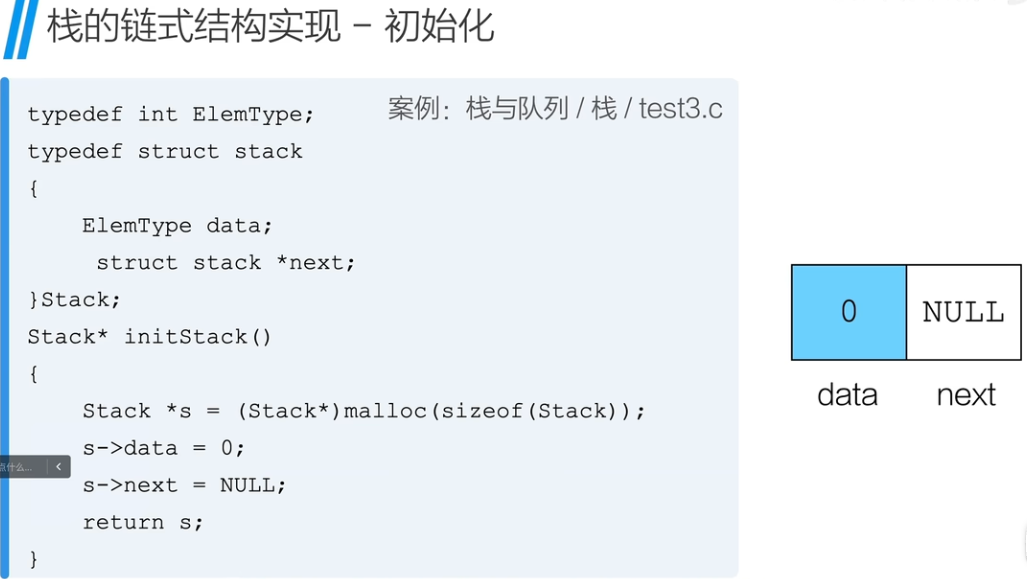
栈的链式结构 - 初始化
栈的链式结构 - 判断是否为空

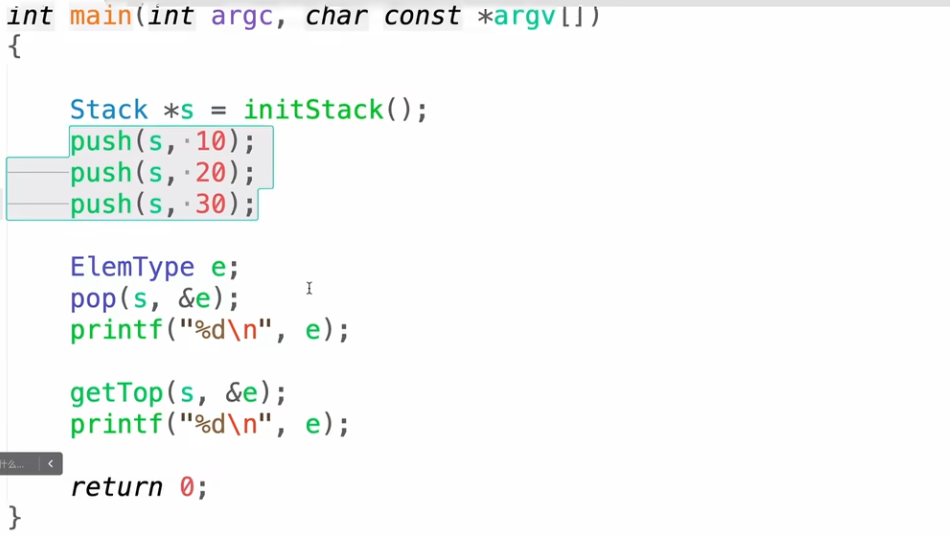
栈的链式结构 - 进栈
类似链表头插法

栈的链式结构 - 出栈





栈的链式结构 - 获取栈顶元素

3、队列
队列的创建


队列 - 初始化

队列 - 判断是否为空

队列 - 出队
注:顺序结构删除元素,实际都是通过改变下标实现的,并不是真正的删除

队列 - 入队

队列 - 获取队头数据

队列 - 动态内存分配
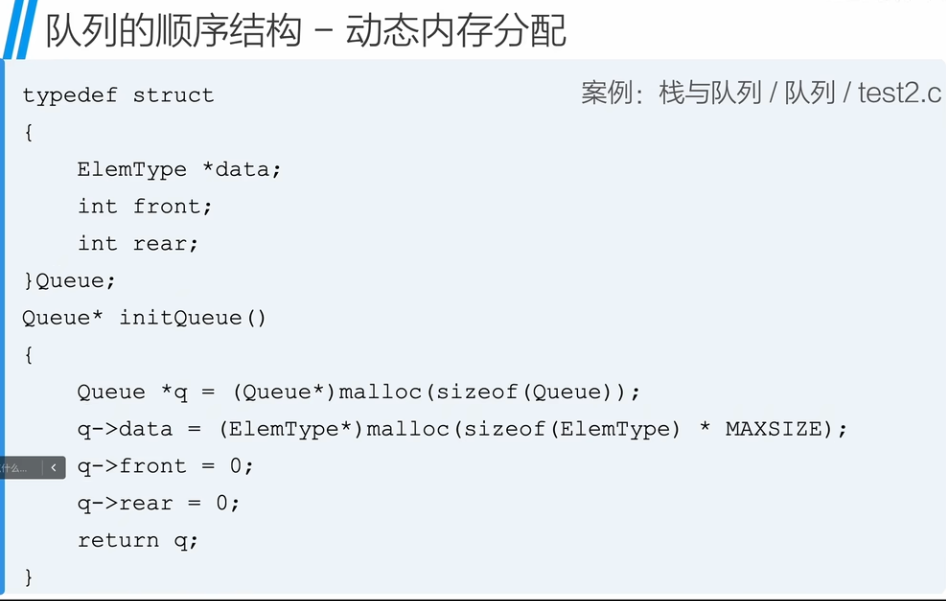
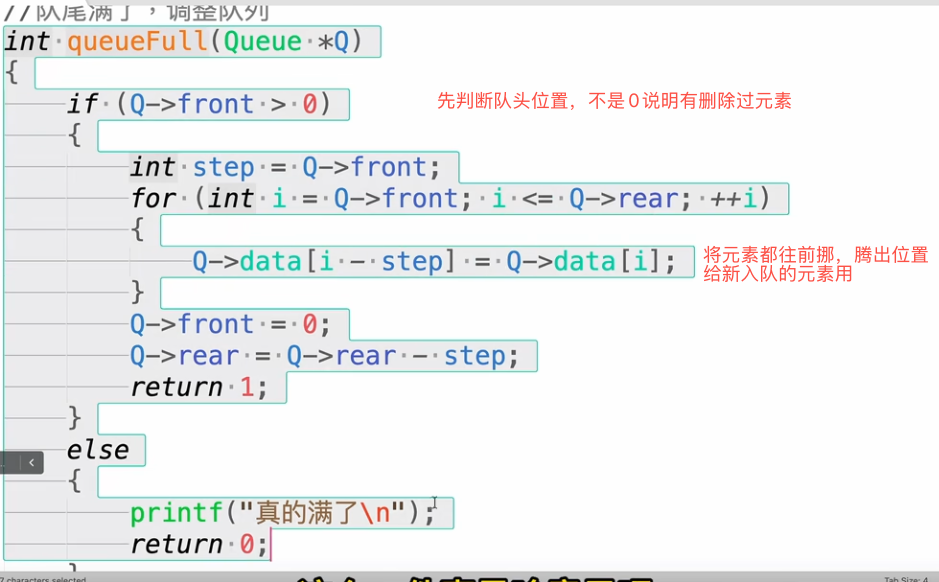
4、循环队列
循环队列的创建
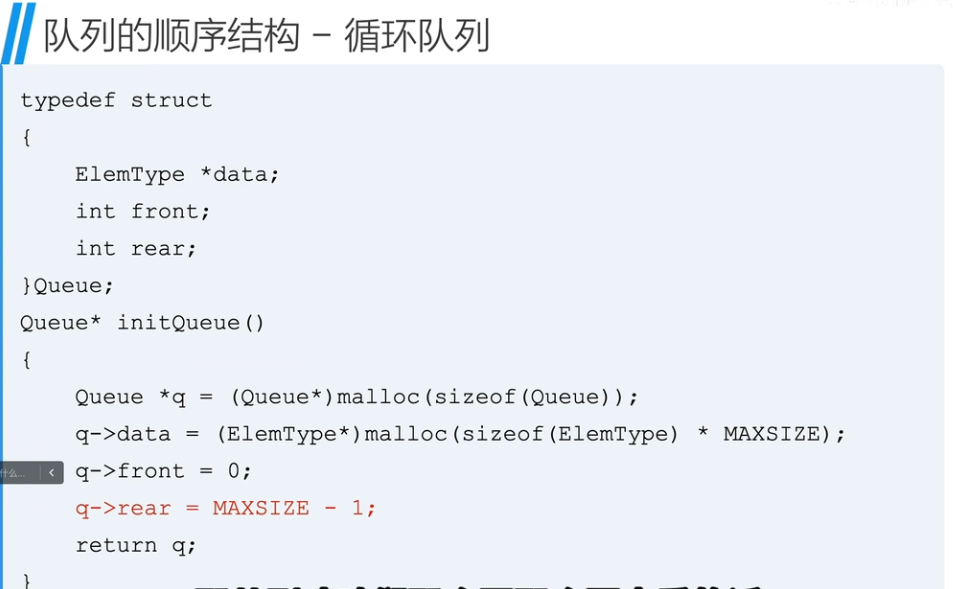
循环队列 - 入队

循环队列 - 出队

5、队列的链式结构
队列的链式结构创建

队列的链式结构 - 初始化

队列的链式结构 - 入队

队列的链式结构 - 出队

四、树
1、树的介绍
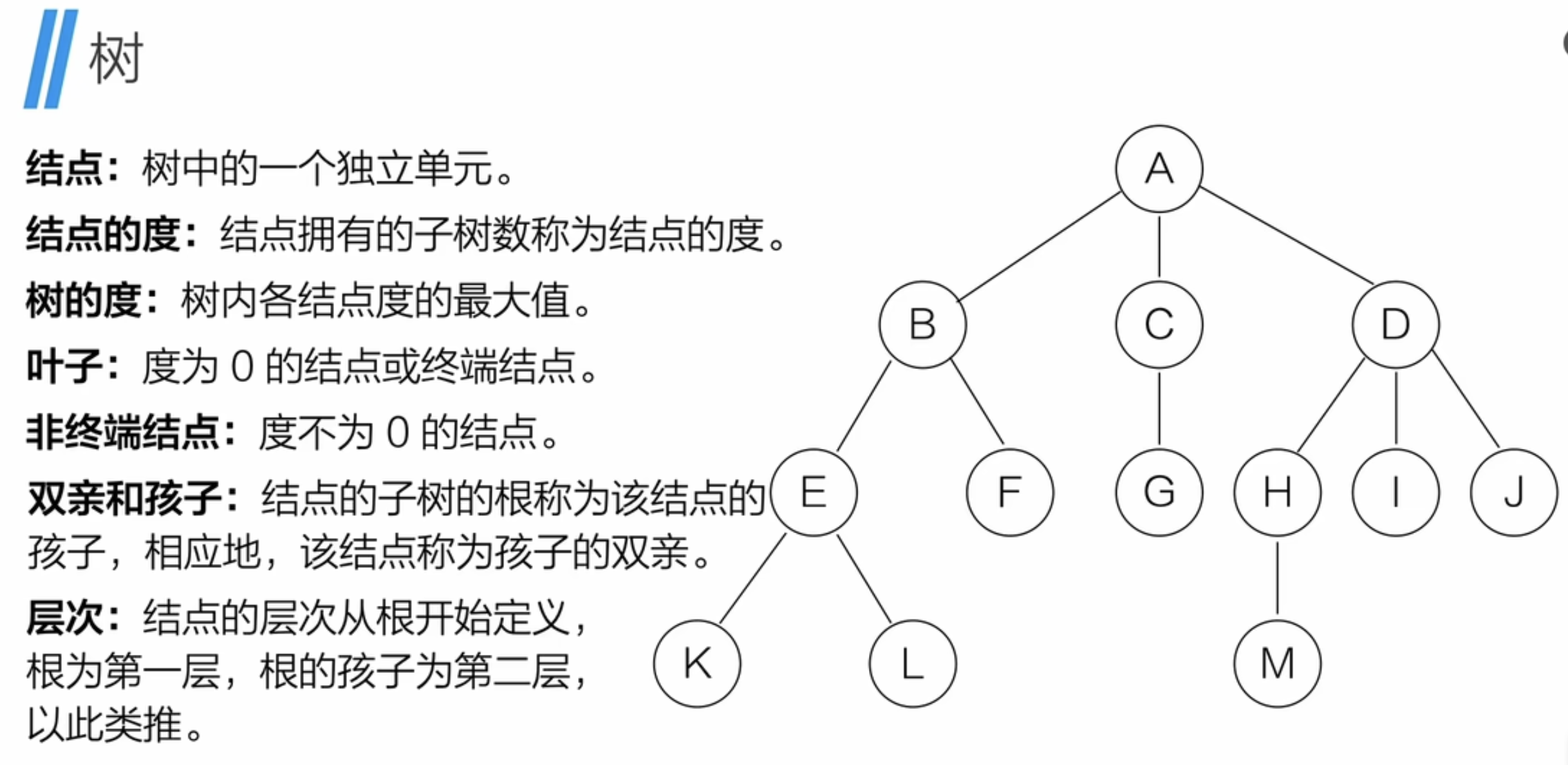
2、树的基本性质
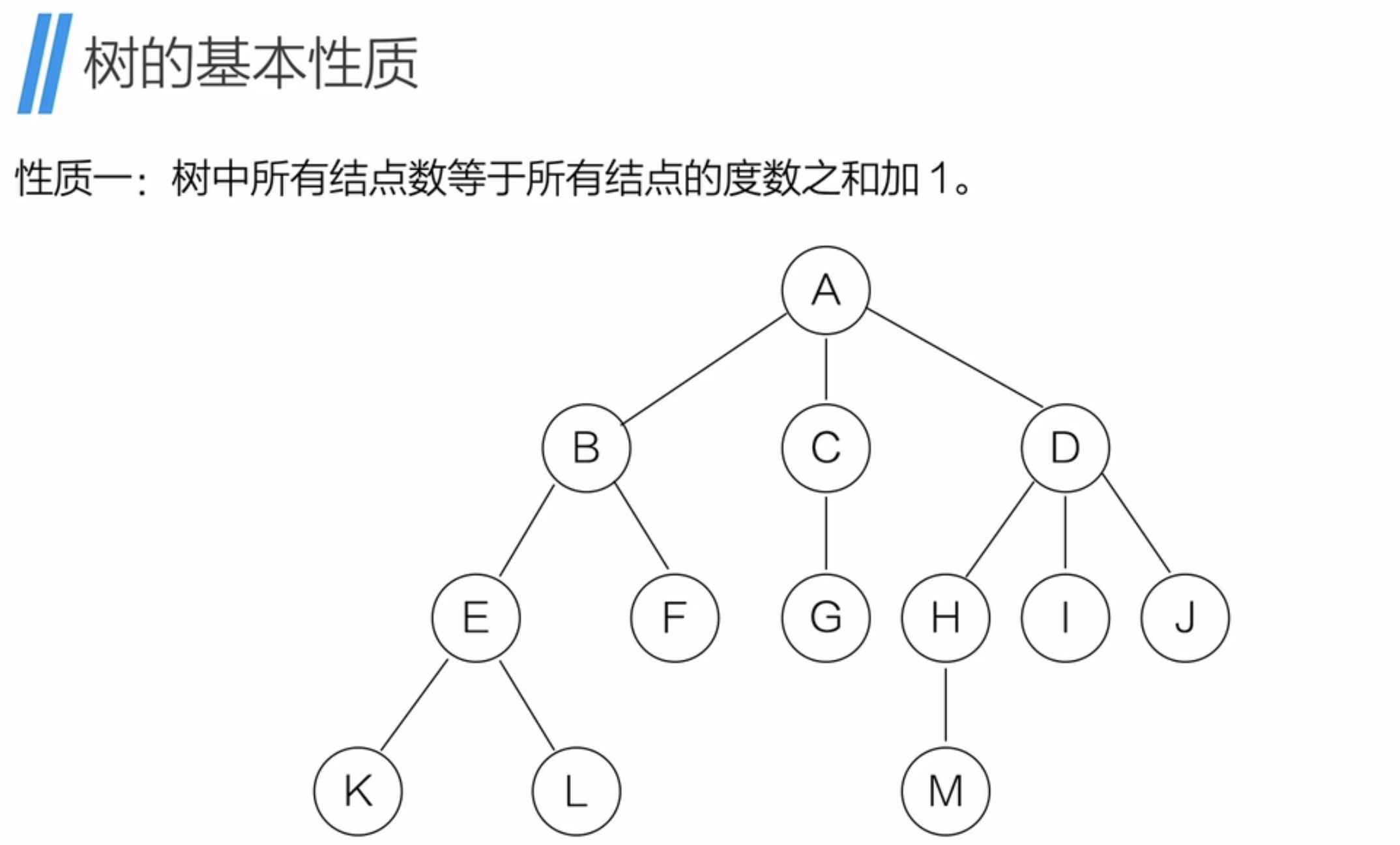
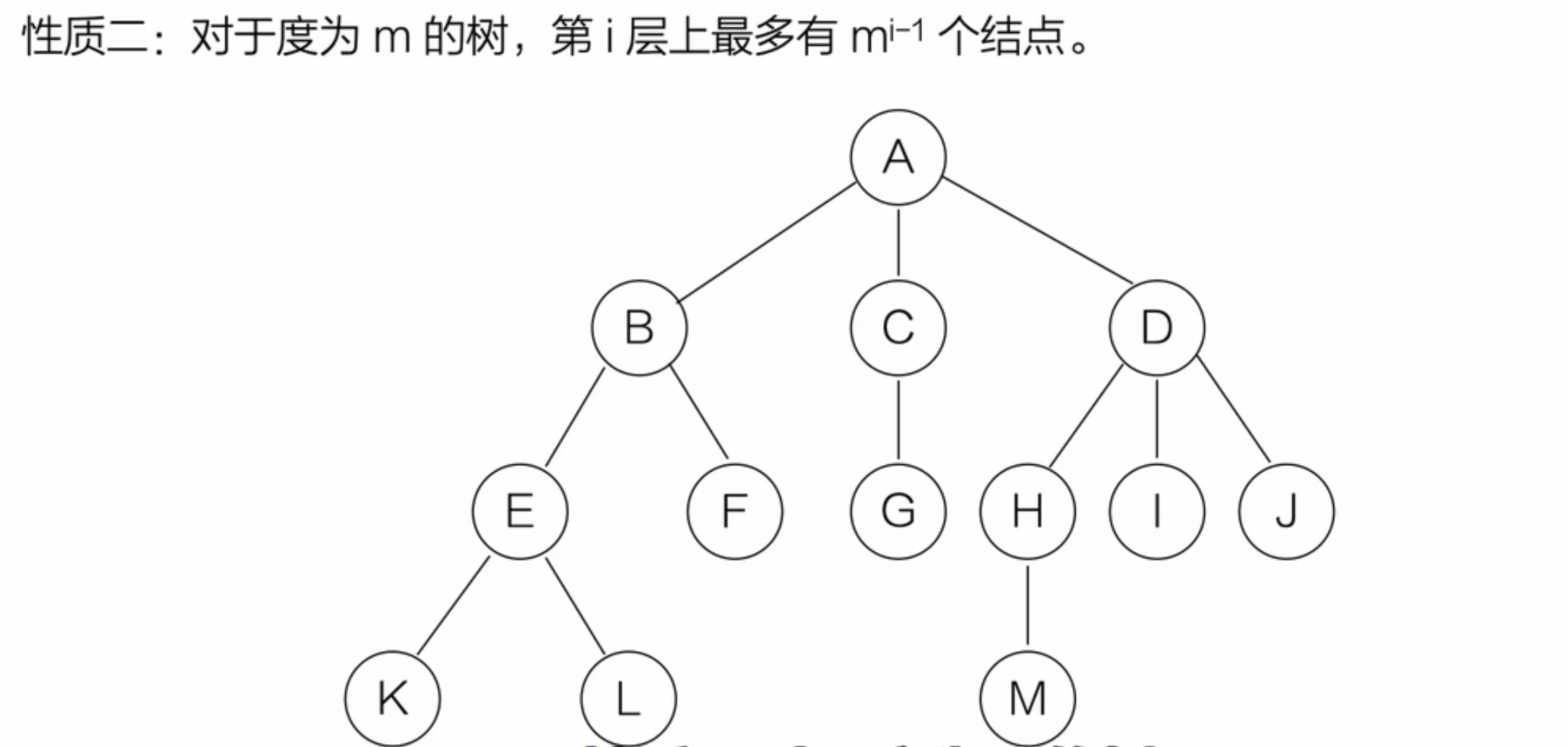

3、二叉树的介绍
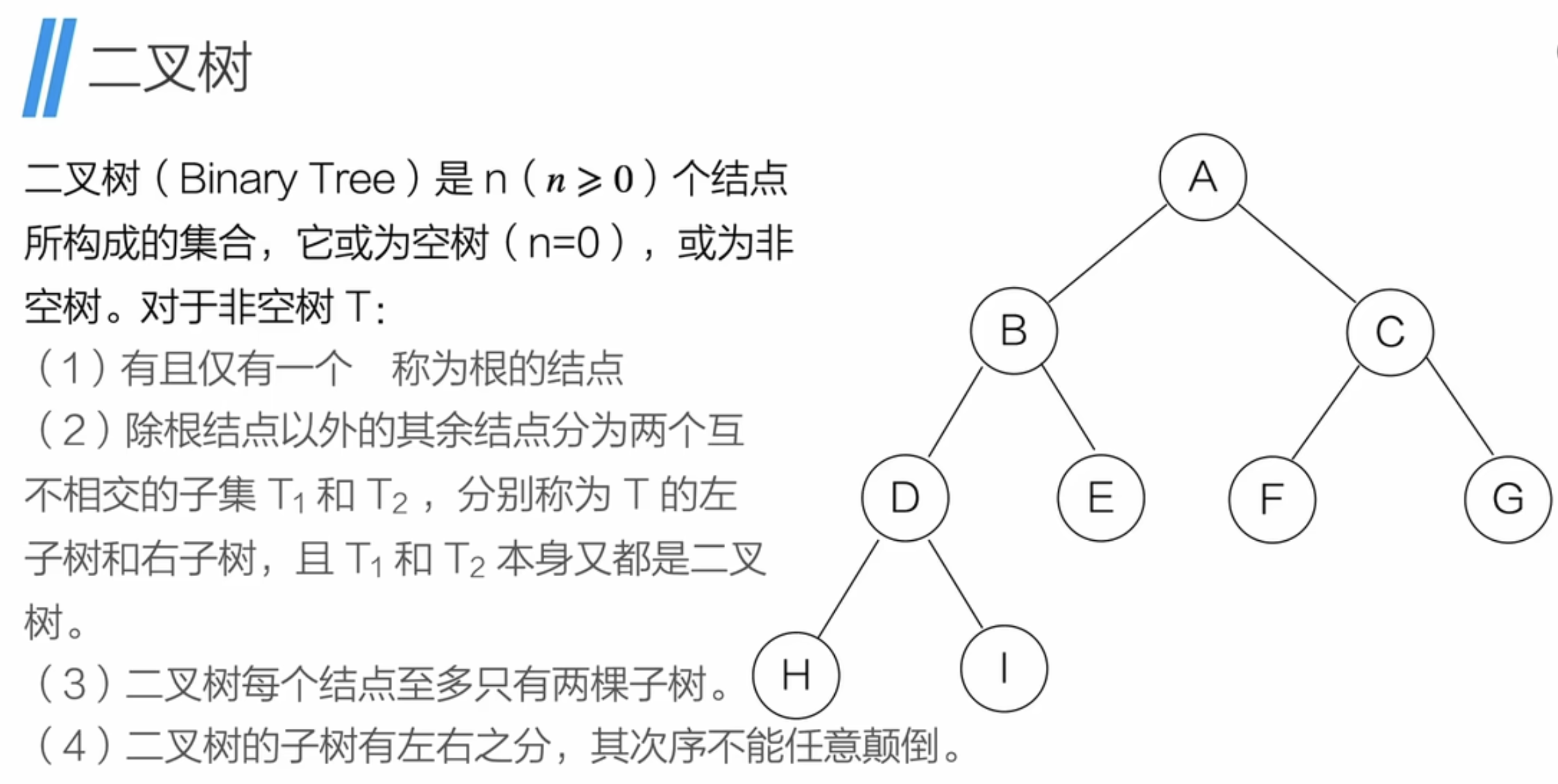
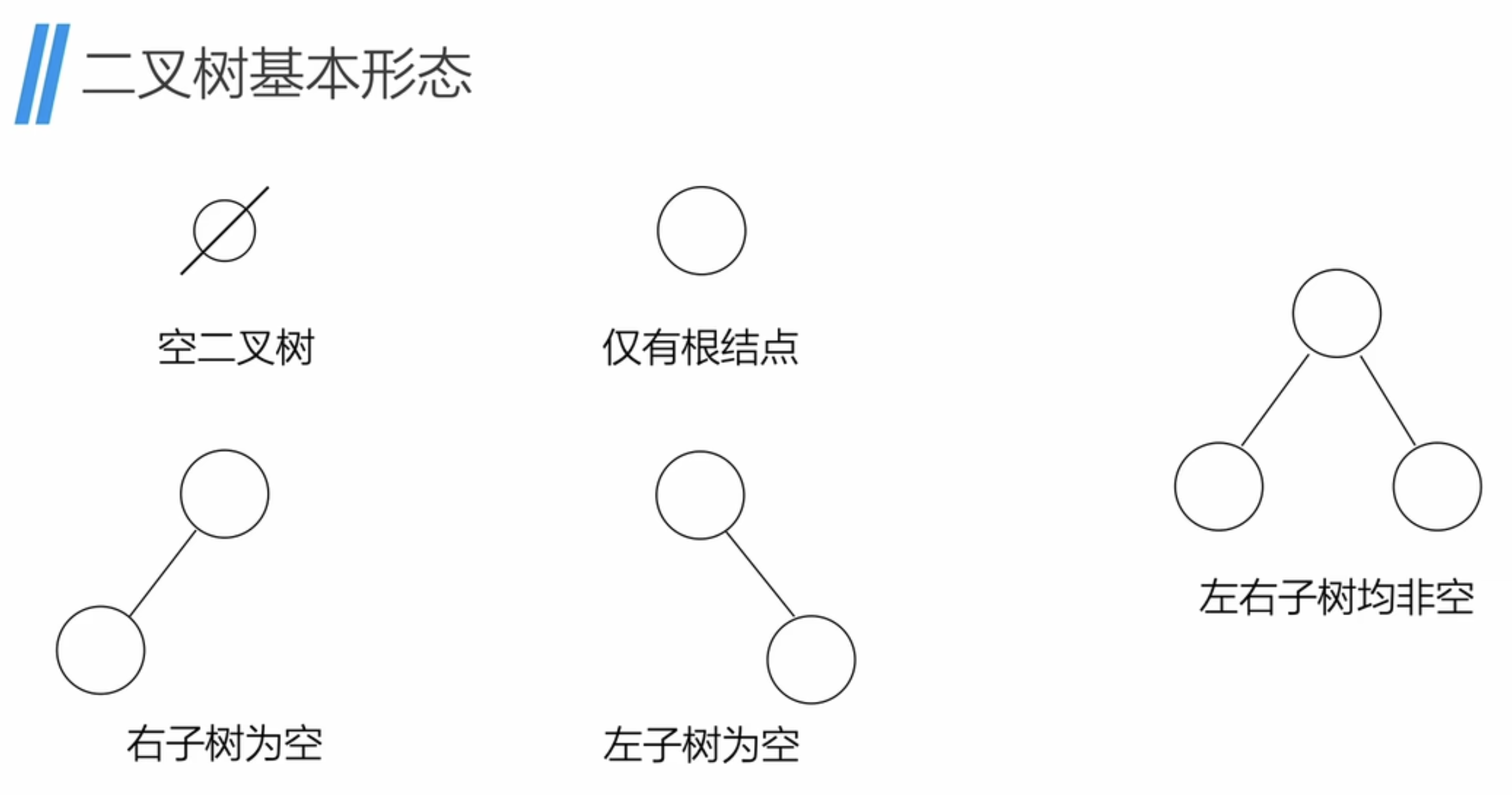
4、二叉树的性质
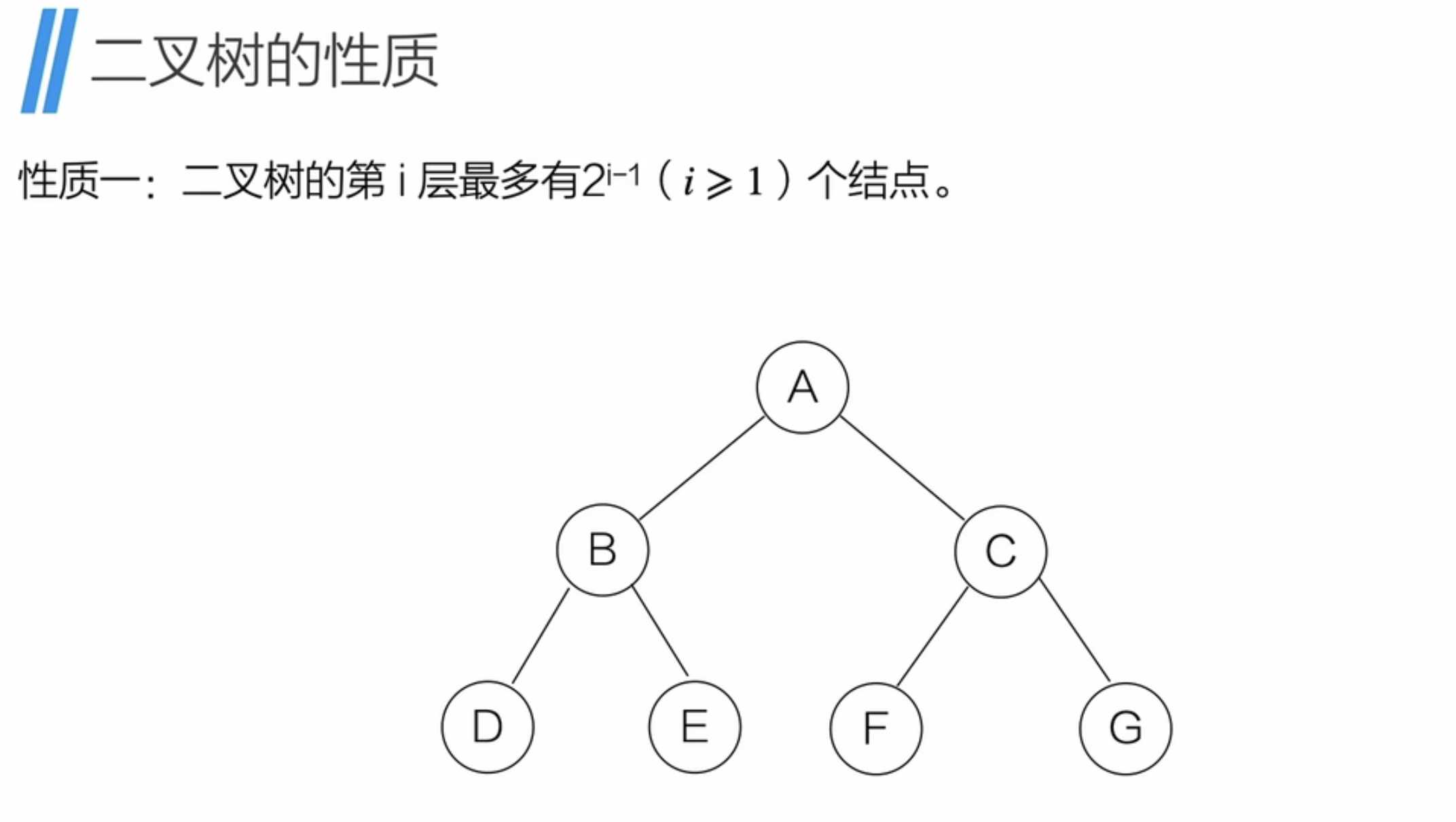
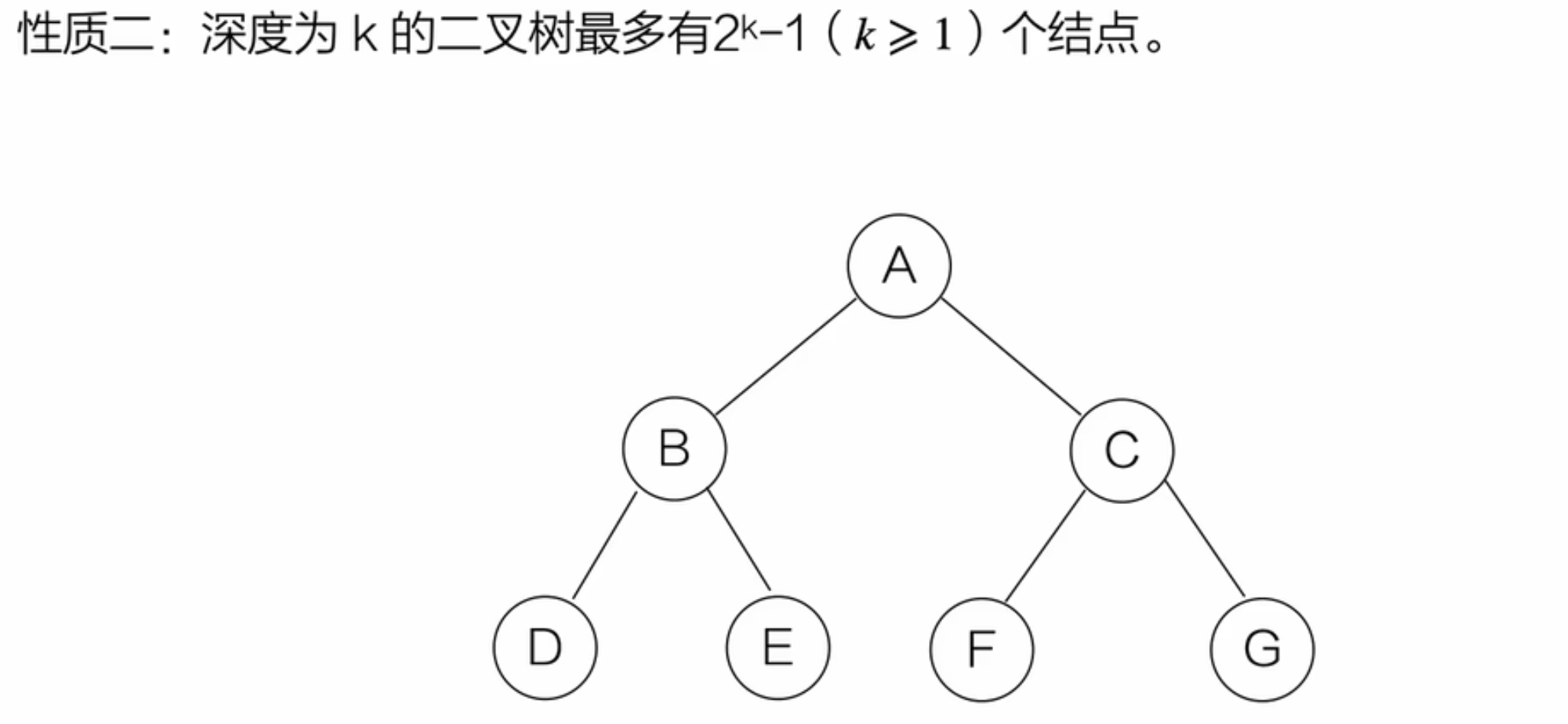
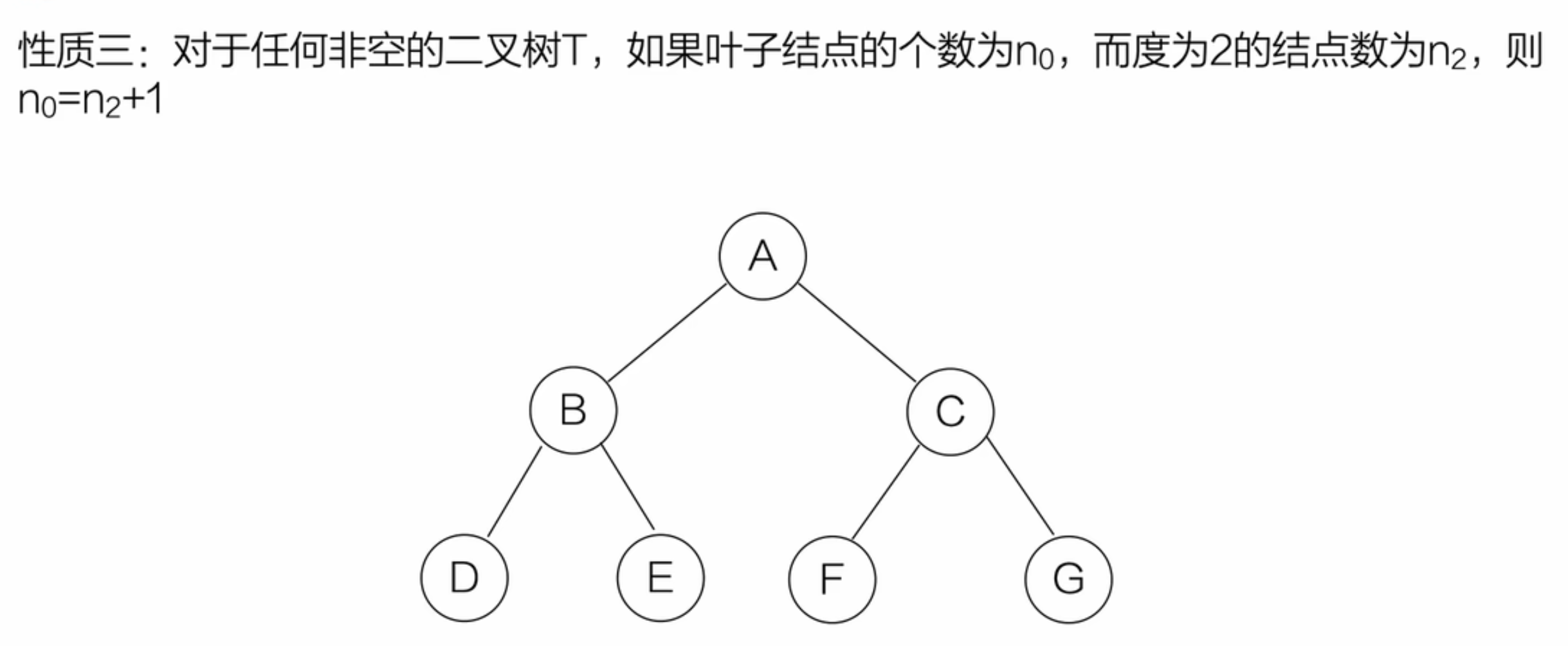
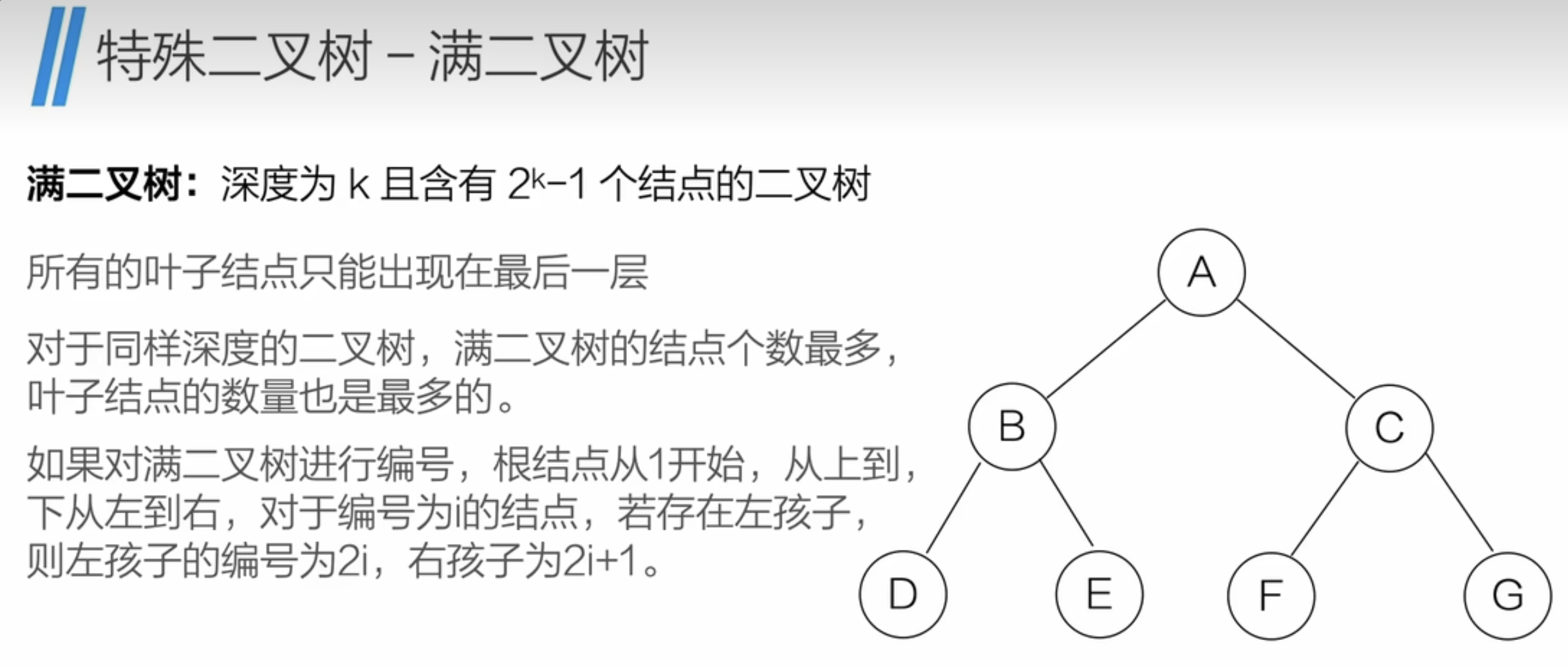
满二叉树
完全二叉树
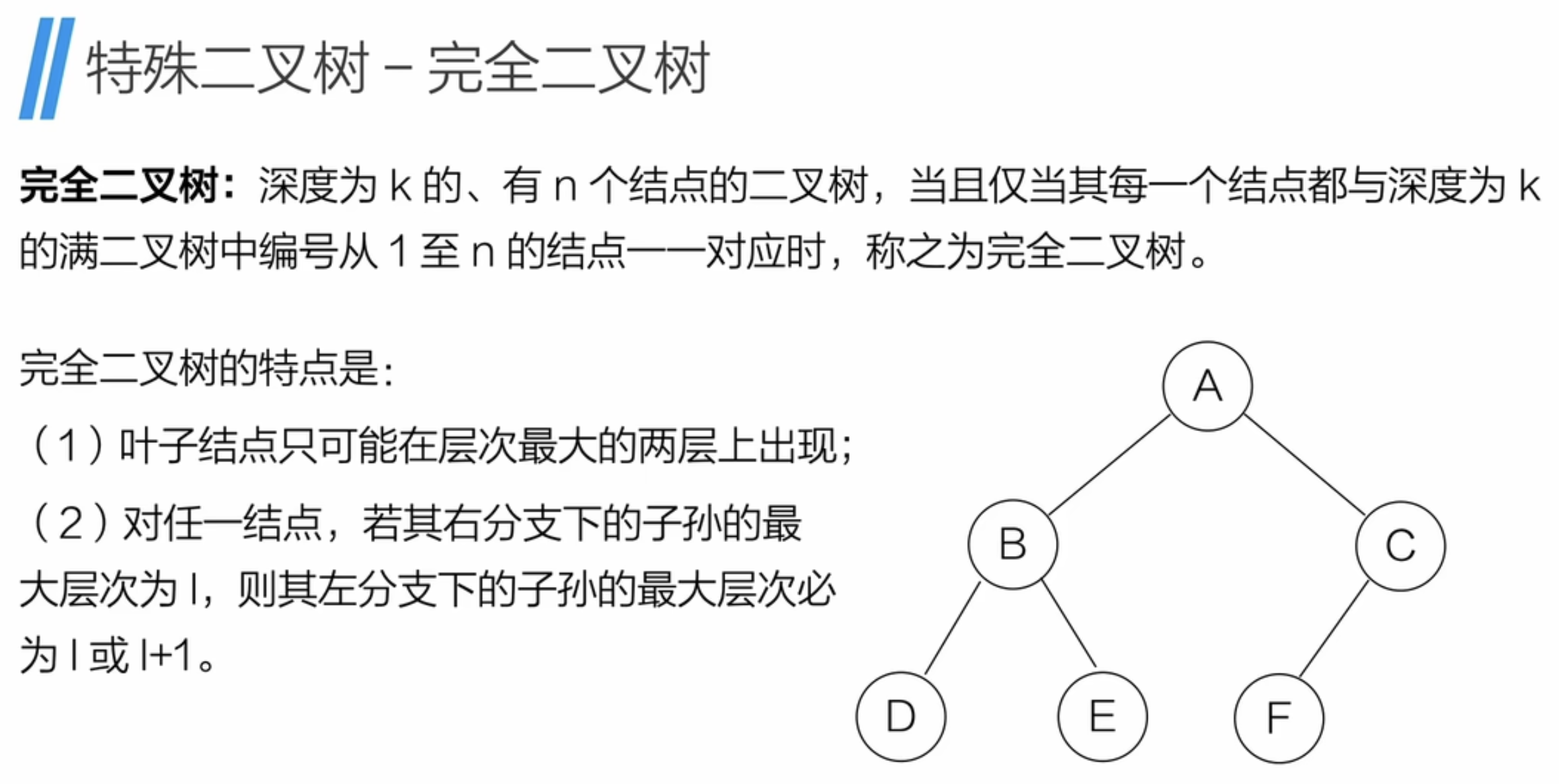
5、二叉树的存储结构
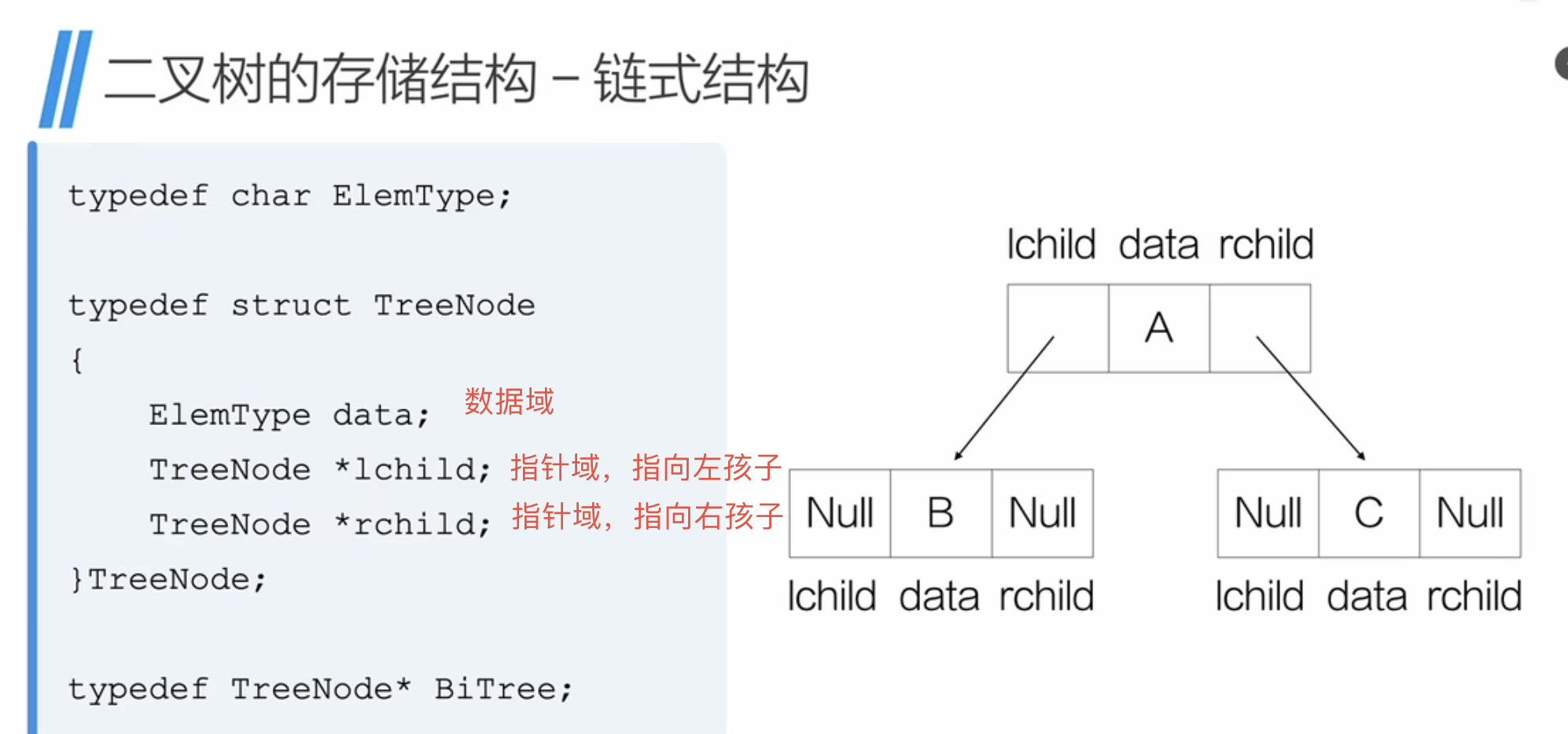
前序遍历
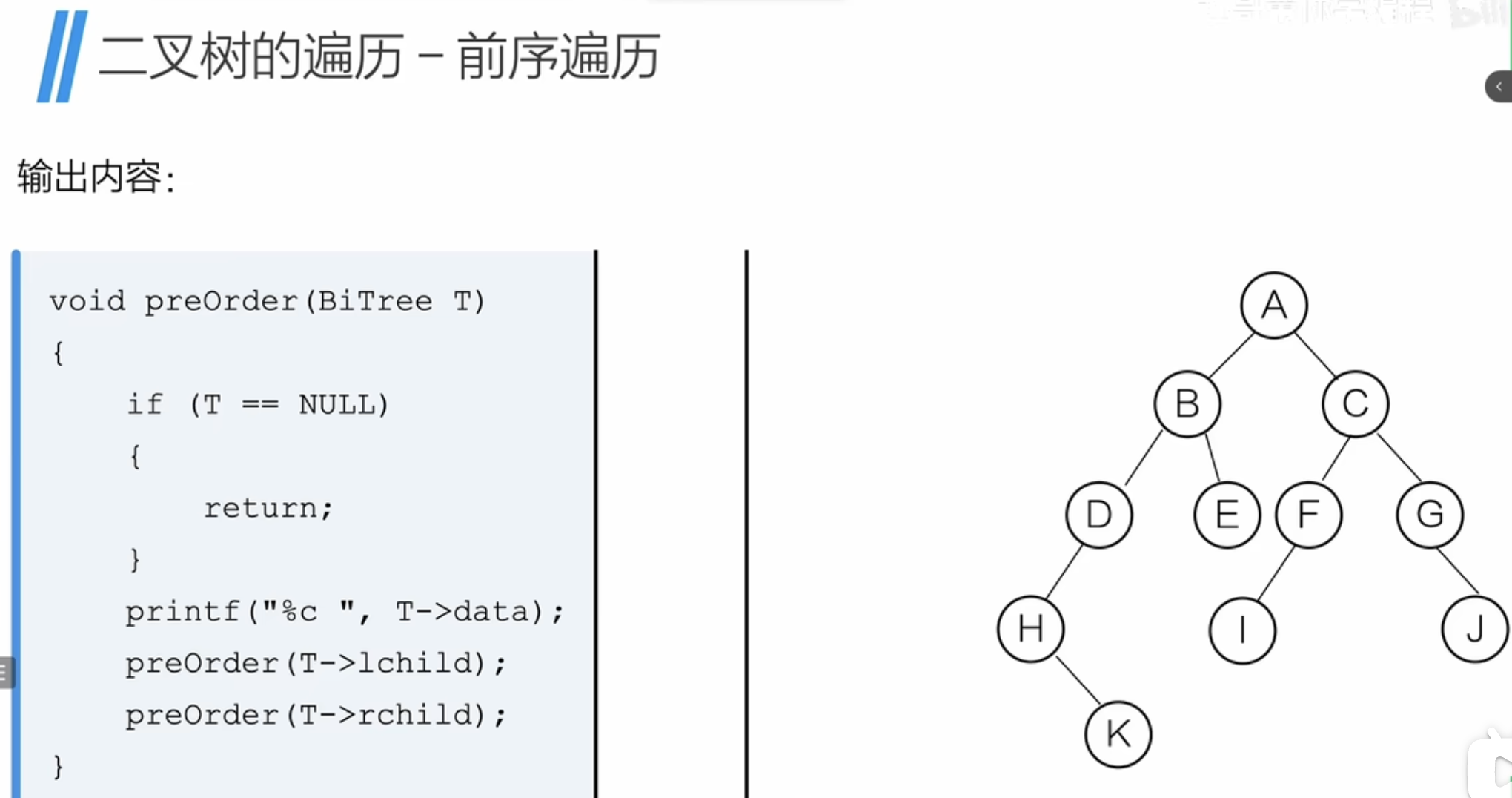



sss