【S组篇】C++知识点总结(1)：并查集基础

AICodeThunder2025-10-26 11:18

并查集基础

一、基础

1. 概念

并查集是一种用于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素。

顾名思义，并查集支持两种操作：

  • 合并（Union）：合并两个元素所属集合（合并对应的树）
  • 查询（Find） ：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合

2. 初始化

初始时，每个元素都位于一个单独的集合，表示为一棵只有根节点的树。方便起见，我们将根节点的父亲设为自己。

3. 合并

要合并两棵树，我们只需要将一棵树的根节点连到另一棵树的根节点。

4. 查询

我们需要沿着树向上移动，直至找到根节点。

二、模板

题目描述

现在有一个并查集，你需要完成合并和查询操作。

输入格式

第一行包含两个整数 N , M N,M N,M，表示共有 N N N 个元素和 M M M 个操作。

接下来 M M M 行，每行包含三个整数 Z i , X i , Y i Z_i,X_i,Y_i Zi,Xi,Yi。

当 Z i = 1 Z_i=1 Zi=1 时，将 X i X_i Xi 与 Y i Y_i Yi 所在的集合合并。

当 Z i = 2 Z_i=2 Zi=2 时，输出 X i X_i Xi 与 Y i Y_i Yi 是否在同一集合内，是的输出 'Y'，否则输出 'N'。

输出格式

对于每一个 Z i = 2 Z_i=2 Zi=2 的操作，都有一行输出，每行包含一个大写字母，为 'Y' 或者 'N'。

输入输出样例

输入 #1

复制代码 
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4

输出 #1

复制代码 
N
Y
N
Y

说明/提示

对于 30 % 30\% 30% 的数据， N ≤ 10 , M ≤ 20 N\le10,M\le20 N≤10,M≤20。

对于 70 % 70\% 70% 的数据， N ≤ 100 , M ≤ 1 0 3 N\le100,M\le10^3 N≤100,M≤103。

对于 100 % 100\% 100% 的数据， 1 ≤ N ≤ 1 0 4 , 1 ≤ M ≤ 2 × 1 0 5 1\le N\le10^4,1\le M\le2\times10^5 1≤N≤104,1≤M≤2×105。

参考答案

70 Pts

完全按照基础思路进行书写。

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e4+8;
int n,m,dsu[MAXN];//Disjoint Set Union，功能类似fa[]
int find(int u){//找根节点
    if(dsu[u]==u)//是根节点
        return u;
    return find(dsu[u]);//找上一层
}
void unite(int u,int v){//合并u和v
    dsu[find(u)]=find(v);//将一棵树的根节点连到另一棵树的根节点
}
int main(){
    cin>>n>>m;
    //初始化，将所有节点的父亲设为自己
    for(int i=1;i<=n;i++)dsu[i]=i;
    for(int i=1,op,u,v;i<=m;i++){
        cin>>op>>u>>v;
        if(op==1)unite(u,v);
        else cout<<(find(u)==find(v)?"Y\n":"N\n");//u、v有相同根节点就属于同一集合
    }
    return 0;
}

100 Pts

并查集的两个优化：

  • 按秩合并 ：维护树的秩（通常为树的高度或节点数的对数）。每次合并时，将秩较小的树合并到秩较大的树下。秩的更新规则为：若两树秩相同，合并后根节点的秩加 1 1 1；否则不更新。
  • 路径压缩：查询过程中经过的每个元素都属于该集合，我们可以将其直接连到根节点以加快后续查询。

这里给出用路径压缩优化的版本。

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e4+8;
int n,m,dsu[MAXN];//Disjoint Set Union，功能类似fa[]
int find(int u){//找根节点
    //if(dsu[u]==u)//是根节点
    //    return u;
    //return dsu[u]=find(dsu[u]);//路径压缩，将同一路径上的点连接到根节点，并找上一层
    return dsu[u]==u?u:dsu[u]=find(dsu[u]);
}
void unite(int u,int v){//合并u和v
    dsu[find(u)]=find(v);//将一棵树的根节点连到另一棵树的根节点
}
int main(){
    cin>>n>>m;
    //初始化，将所有节点的父亲设为自己
    for(int i=1;i<=n;i++)dsu[i]=i;
    for(int i=1,op,u,v;i<=m;i++){
        cin>>op>>u>>v;
        if(op==1)unite(u,v);
        else cout<<(find(u)==find(v)?"Y\n":"N\n");//u、v有相同根节点就属于同一集合
    }
    return 0;
}

三、例题

1. P1536 村村通

题目描述

某市调查城镇交通状况，得到现有城镇道路统计表。表中列出了每条道路直接连通的城镇。市政府"村村通工程"的目标是使全市任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要相互之间可达即可）。请你计算出最少还需要建设多少条道路？

输入格式

输入包含若干组测试测试数据，每组测试数据的第一行给出两个用空格隔开的正整数，分别是城镇数目 n n n 和道路数目 m m m ；随后的 m m m 行对应 m m m 条道路，每行给出一对用空格隔开的正整数，分别是该条道路直接相连的两个城镇的编号。简单起见，城镇从 1 1 1 到 n n n 编号。

注意：两个城市间可以有多条道路相通。

输出格式

对于每组数据，对应一行一个整数。表示最少还需要建设的道路数目。

输入输出样例

输入 #1

复制代码 
4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

输出 #1

复制代码 
1
0
2
998

说明/提示

对于 100 % 100\% 100% 的数据，保证 1 ≤ n ≤ 1000 1≤n≤1000 1≤n≤1000。

参考答案

思路：找出独立的树的数量，需要的道路为将这些独立的树连接成森林的数量，即树的数量 − 1 -1 −1（这里独立的树即连通分量）。

p.s. 这其实是并查集维护连通性的一道经典题目。

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e3+8;
int n,m,dsu[MAXN];
int find(int u){return dsu[u]==u?u:dsu[u]=find(dsu[u]);}
void unite(int u,int v){dsu[find(u)]=find(v);}
int main(){
    while(cin>>n>>m){
        for(int i=1;i<=n;i++)dsu[i]=i;
        for(int i=1,u,v;i<=m;i++){
            cin>>u>>v;
            unite(u,v);
        }
        int cnt=0;//cnt为根节点数量
        for(int i=1;i<=n;i++)
            if(find(i)==i)
                cnt++;
        cout<<cnt-1<<"\n";
        /*
        也可以换一种思路，将所有连通分量合并到 1 所在的连通分量：
        int cnt=0;//cnt为需要的道路数量
        for(int i=1;i<=n;i++)
        	if(find(i)!=find(1))
        		unite(i,1),cnt++;
       	cout<<cnt<<"\n";
        */
    }
    return 0;
}

2. P2814 家谱

题目背景

现代的人对于本家族血统越来越感兴趣。

题目描述

给出充足的父子关系，请你编写程序找到某个人的最早的祖先。

输入格式

输入由多行组成，首先是一系列有关父子关系的描述，其中每一组父子关系中父亲只有一行，儿子可能有若干行，用 #name 的形式描写一组父子关系中的父亲的名字，用 +name 的形式描写一组父子关系中的儿子的名字；接下来用 ?name 的形式表示要求该人的最早的祖先；最后用单独的一个 $ 表示文件结束。

输出格式

按照输入文件的要求顺序，求出每一个要找祖先的人的祖先，格式为：本人的名字 + + + 一个空格 + + + 祖先的名字 + + + 回车。

输入输出样例

输入 #1

复制代码 
#George
+Rodney
#Arthur
+Gareth
+Walter
#Gareth
+Edward
?Edward
?Walter
?Rodney
?Arthur
$

输出 #1

复制代码 
Edward Arthur
Walter Arthur
Rodney George
Arthur Arthur

说明/提示

规定每个人的名字都有且只有 6 6 6 个字符，而且首字母大写，且没有任意两个人的名字相同。最多可能有 1 0 3 10^3 103 组父子关系，总人数最多可能达到 5 × 1 0 4 5 \times 10^4 5×104 人，家谱中的记载不超过 30 30 30 代。

参考答案

思路：只需要将 dsu[] 改为 map 类型即可，并修改为每读入一个人名就对这个人名做一次初始化。

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
map<string,string>dsu;
string find(string u){return dsu[u]==u?u:dsu[u]=find(dsu[u]);}
void unite(string u,string v){dsu[find(u)]=find(v);}
int main(){
    char op;
    string fa,name;//fa临时存储父亲的名字
    while(cin>>op&&op!='$'){
        cin>>name;
        if(dsu[name]=="")dsu[name]=name;//初始化
        if(op=='#')fa=name;
        else if(op=='+')dsu[name]=fa;
        else if(op=='?')cout<<name<<" "<<find(name)<<"\n";
    }
    return 0;
}

3. P2078 朋友

题目背景

小明在 A 公司工作，小红在 B 公司工作。

题目描述

这两个公司的员工有一个特点：一个公司的员工都是同性。

A 公司有 N N N 名员工，其中有 P P P 对朋友关系。B 公司有 M M M 名员工，其中有 Q Q Q 对朋友关系。朋友的朋友一定还是朋友。

每对朋友关系用两个整数 ( X i , Y i ) (X_i,Y_i) (Xi,Yi) 组成，表示朋友的编号分别为 X i , Y i X_i,Y_i Xi,Yi。男人的编号是正数，女人的编号是负数。小明的编号是 1 1 1，小红的编号是 − 1 -1 −1。

大家都知道，小明和小红是朋友，那么，请你写一个程序求出两公司之间，通过小明和小红认识的人最多一共能配成多少对情侣（包括他们自己）。

输入格式

输入的第一行，包含 4 4 4 个空格隔开的正整数 N , M , P , Q N,M,P,Q N,M,P,Q。

之后 P P P 行，每行两个正整数 X i , Y i X_i,Y_i Xi,Yi。

之后 Q Q Q 行，每行两个负整数 X i , Y i X_i,Y_i Xi,Yi。

输出格式

输出一行一个正整数，表示通过小明和小红认识的人最多一共能配成多少对情侣（包括他们自己）。

输入输出样例

输入 #1

复制代码 
4 3 4 2
1 1
1 2
2 3
1 3
-1 -2
-3 -3

输出 #1

复制代码 
2

说明/提示

对于 30 % 30 \% 30% 的数据， N , M ≤ 100 N,M \le 100 N,M≤100， P , Q ≤ 200 P,Q \le 200 P,Q≤200；

对于 80 % 80 \% 80% 的数据， N , M ≤ 4 × 1 0 3 N,M \le 4 \times 10^3 N,M≤4×103， P , Q ≤ 1 0 4 P,Q \le 10^4 P,Q≤104；

对于 100 % 100 \% 100% 的数据， N , M ≤ 1 0 4 N,M \le 10^4 N,M≤104， P , Q ≤ 2 × 1 0 4 P,Q \le 2 \times 10^4 P,Q≤2×104。

参考答案

新知识点：集合大小维护

思路：在每个集合的根节点处附加一个 sz[] 记录每个集合的大小。合并两棵树前，我们还需要将一棵树的大小合并到另一棵树的根节点上。

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e4+8;
int n,m,p,q;
map<int,int>dsu,sz;
int find(int u){return dsu[u]==u?u:dsu[u]=find(dsu[u]);}
void unite(int u,int v){
    int fu=find(u),fv=find(v);
    if(fu==fv)return;
    dsu[fu]=fv,sz[fv]+=sz[fu];//维护大小
}
int main(){
    cin>>n>>m>>p>>q;
    for(int i=1,u,v;i<=p+q;i++){
        cin>>u>>v;
        //初始化
        if(dsu[u]==0)dsu[u]=u,sz[u]=1;
        if(dsu[v]==0)dsu[v]=v,sz[v]=1;
        unite(u,v);
    }
    cout<<min(sz[find(1)],sz[find(-1)]);//显然A公司和B公司的人数的最小值为情侣数，剩下几个是单身狗
    return 0;
}

4. P1661 扩散

题目描述

一个点每过一个单位时间就会向四个方向扩散一个距离，如图。

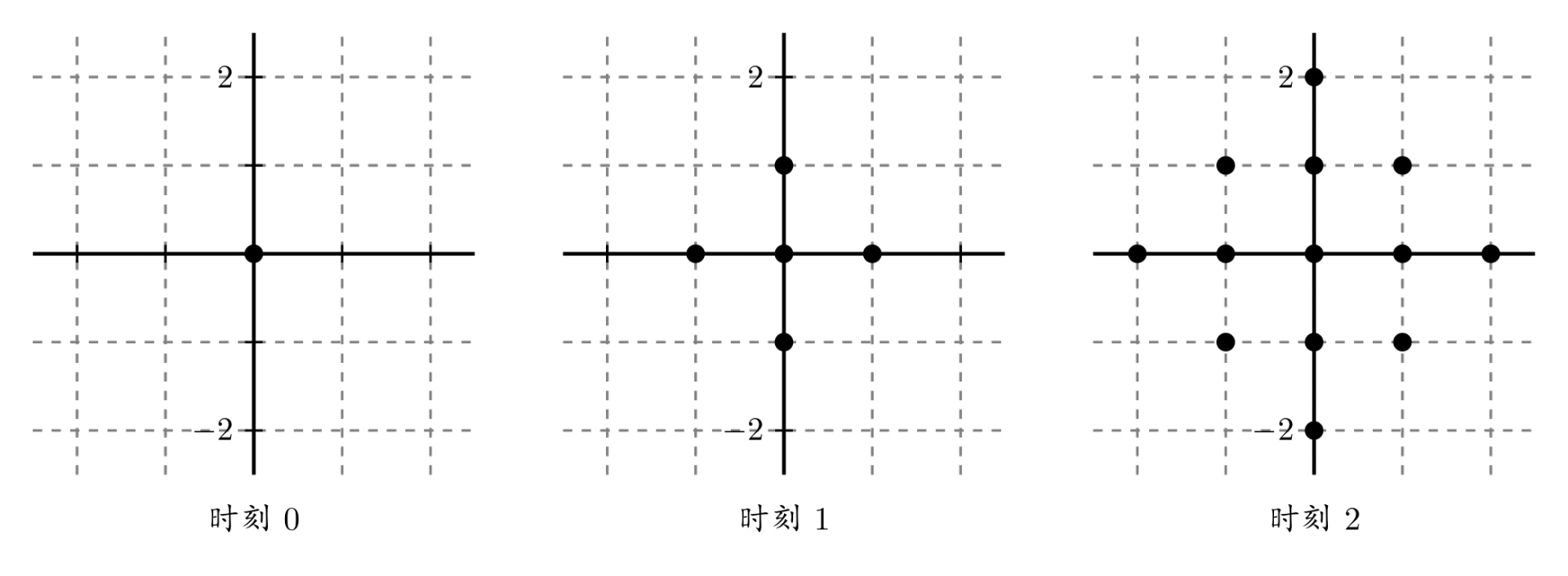
两个点 a a a 、 b b b 连通，记作 e ( a , b ) e(a,b) e(a,b)，当且仅当 a , b a,b a,b 的扩散区域有公共部分。连通块的定义是块内的任意两个点 u , v u,v u,v 都必定存在路径 e ( u , a 0 ) , e ( a 0 , a 1 ) , ⋯   , e ( a k , v ) e(u,a_0),e(a_0,a_1),\cdots,e(a_k,v) e(u,a0),e(a0,a1),⋯,e(ak,v)。给定平面上的 n n n 个点，问最早什么时刻它们形成一个连通块。

输入格式

第一行一个数 n n n，以下 n n n 行，每行一个点坐标。

输出格式

一个数，表示最早的时刻所有点形成连通块。

输入输出样例

输入 #1

复制代码 
2
0 0
5 5

输出 #1

复制代码 
5

说明/提示

对于 20 % 20\% 20% 的数据，满足 1 ≤ N ≤ 5 ; 1 ≤ X i , Y i ≤ 50 1 \le N \le 5;1 \le X_i,Y_i \le 50 1≤N≤5;1≤Xi,Yi≤50。

对于 100 % 100\% 100% 的数据，满足 1 ≤ N ≤ 50 1 \le N \le 50 1≤N≤50， 1 ≤ X i , Y i ≤ 1 0 9 1 \le X_i,Y_i \le 10^9 1≤Xi,Yi≤109。

参考答案

预备知识点：

求任意两点之间的距离：
dist ( u , v ) = ∣ x u − x v ∣ + ∣ y u − y v ∣ \text{dist}(u,v)=|x_u-x_v|+|y_u-y_v| dist(u,v)=∣xu−xv∣+∣yu−yv∣

思路：使用二分答案找出最小时间，枚举所有的两个点之间的距离和扩散距离的比较。扩散距离最大为 2 t 2t 2t。

参考答案：

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int MAXN=58;
int n,x[MAXN],y[MAXN],dsu[MAXN];
int find(int u){return dsu[u]==u?u:dsu[u]=find(dsu[u]);}
void unite(int u,int v){dsu[find(u)]=find(v);}
int dist(int u,int v){return abs(x[u]-x[v])+abs(y[u]-y[v]);}
bool check(int ans){
    for(int i=1;i<=n;i++)dsu[i]=i;
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
            if(dist(i,j)<=(ans<<1))//两点之间的距离<=扩散距离，至于为什么是 2ans，是因为两点各自扩散距离（半径）之和
                unite(i,j);//两点是连通的
    //类似村村通的循环，判断是否形成一个连通块
    for(int i=1;i<=n;i++)
        if(find(i)!=find(1))
            return false;
    return true;
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)cin>>x[i]>>y[i];
    int l=0,r=1e9,mid;
    while(l<r)mid=(l+r)>>1,check(mid)?r=mid:l=mid+1;
    cout<<l;
    return 0;
}

5. [BalticOI 2003] 团伙

题目描述

现在有 n n n 个人，他们之间有两种关系：朋友和敌人。我们知道：

  • 一个人的朋友的朋友是朋友
  • 一个人的敌人的敌人是朋友

现在要对这些人进行组团。两个人在一个团体内当且仅当这两个人是朋友。请求出这些人中最多可能有的团体数。

输入格式

第一行输入一个整数 n n n 代表人数。

第二行输入一个整数 m m m 表示接下来要列出 m m m 个关系。

接下来 m m m 行，每行一个字符 o p t opt opt 和两个整数 p , q p,q p,q，分别代表关系（朋友或敌人），有关系的两个人之中的第一个人和第二个人。其中 o p t opt opt 有两种可能：

  • 如果 o p t opt opt 为 F，则表明 p p p 和 q q q 是朋友。
  • 如果 o p t opt opt 为 E，则表明 p p p 和 q q q 是敌人。

输出格式

一行一个整数代表最多的团体数。

输入输出样例

输入 #1

复制代码 
6
4
E 1 4
F 3 5
F 4 6
E 1 2

输出 #1

复制代码 
3

说明/提示

对于 100 % 100\% 100% 的数据， 2 ≤ n ≤ 1000 2 \le n \le 1000 2≤n≤1000， 1 ≤ m ≤ 5000 1 \le m \le 5000 1≤m≤5000， 1 ≤ p , q ≤ n 1 \le p,q \le n 1≤p,q≤n。

参考答案

新知识点：种类并查集

概念：是一种扩展的并查集数据结构，用于处理元素间的多重关系（如朋友和敌人关系），通过将原并查集规模扩大多倍来维护对应关系。

思路：种类并查集将原并查集扩大两倍至多倍规模。以朋友敌人关系为例：前半部分（ 1 1 1 到 n n n）表示朋友集合，后半部分（ n + 1 n+1 n+1 到 2 n 2n 2n）表示敌人集合。这种设计能够将敌对关系转换为朋友关系进行处理，利用"敌人的敌人是朋友"这一性质。

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e3+8;
int n,m,dsu[MAXN<<1];
int find(int u){return dsu[u]==u?u:dsu[u]=find(dsu[u]);}
void unite(int u,int v){dsu[find(u)]=find(v);}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n<<1;i++)dsu[i]=i;//初始化并查集
    for(int i=1,u,v;i<=m;i++){
        char op;
        cin>>op>>u>>v;
        if(op=='F')unite(u,v);
        if(op=='E')unite(v+n,u),unite(u+n,v);
    }
    int ans=0;//统计连通区域个数
    for(int i=1;i<=n;i++)ans+=(dsu[i]==i);
    cout<<ans;
    return 0;
}
相关推荐
南方的狮子先生3 小时前
【逻辑回归】从线性模型到逻辑回归
算法·机器学习·逻辑回归
Wind哥4 小时前
设计模式23种-C++实现
开发语言·c++·windows·设计模式
闻缺陷则喜何志丹4 小时前
【排序】P9127 [USACO23FEB] Equal Sum Subarrays G|普及+
c++·算法·排序·洛谷
傲世（C/C++,Linux）4 小时前
C标准库-时间函数
c语言
moringlightyn4 小时前
c++ 智能指针
开发语言·c++·笔记·c++11·指针·智能指针
Code_Shark4 小时前
AtCoder Beginner Contest 424 题解
数据结构·c++·算法·数学建模·青少年编程
CS创新实验室4 小时前
深入解析快速排序（Quicksort）：从原理到实践
数据结构·算法·排序算法·快速排序
今天又在学代码写BUG口牙4 小时前
MFC应用程序，工作线程学习记录
c++·mfc·1024程序员节
j_xxx404_4 小时前
C++ STL简介：从原理到入门使用指南
开发语言·c++
热门推荐
01BongoCat - 跨平台键盘猫动画工具02GitHub 镜像站点03UV安装并设置国内源04Linux下V2Ray安装配置指南05jdk21下载、安装（Windows、Linux、macOS）06GitLab 零基础入门指南：从安装到项目管理全流程07NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南08Labelme从安装到标注：零基础完整指南09KGG转MP3工具|非KGM文件|解密音频10安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）