牛客小白月赛126

星轨初途2026-01-02 9:14

文章目录

个人主页：星轨初途

个人专栏：C语言，数据结构，C++学习（竞赛类） 算法及编程题分享

前言

嗨(✪ω✪)！我们又见面啦！在本专栏我将分享我在牛客比赛解题思路

今天是元旦，也2026的第一天，祝大家新年快乐，元旦快乐呀！

题目涉及算法类型

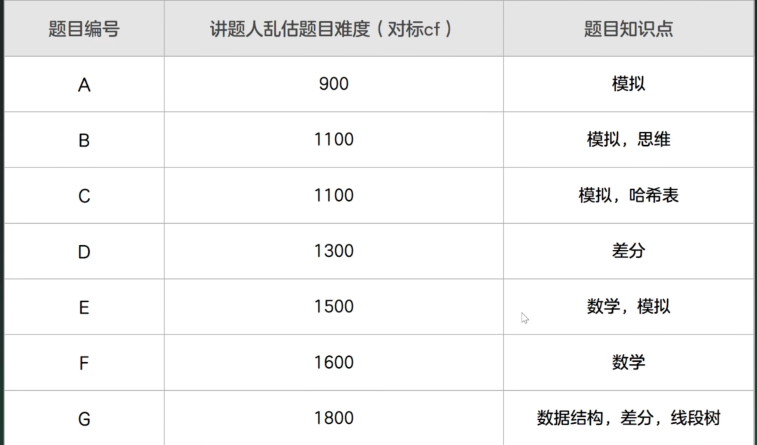
A、小红打舞萌

题目

思路

先比较数字大小，若相等，看是否有"+"

因为我们无法确定输入是否含有字符"+"，所以我们直接用char类型吸收即可，若没有，吸收的为空格（不影响结果）

代码

cpp 复制代码 
#include<iostream>
#include<vector>
using namespace std;
int main()
{
	int t;
	cin >> t;
	while (t--)
	{
		int a, b;
		char a1, b1;
		scanf("%d%c%d%c", &a, &a1, &b, &b1);
		if (a > b)cout << "Yes" << endl;
		else if (a < b)cout << "No" << endl;
		else
		{
			if (a1 == '+')
			{
				if(b1=='+')cout << "No" << endl;
				else cout << "Yes" << endl;

			}
			else
				cout << "No" << endl;
		}
	}
	return 0;
}

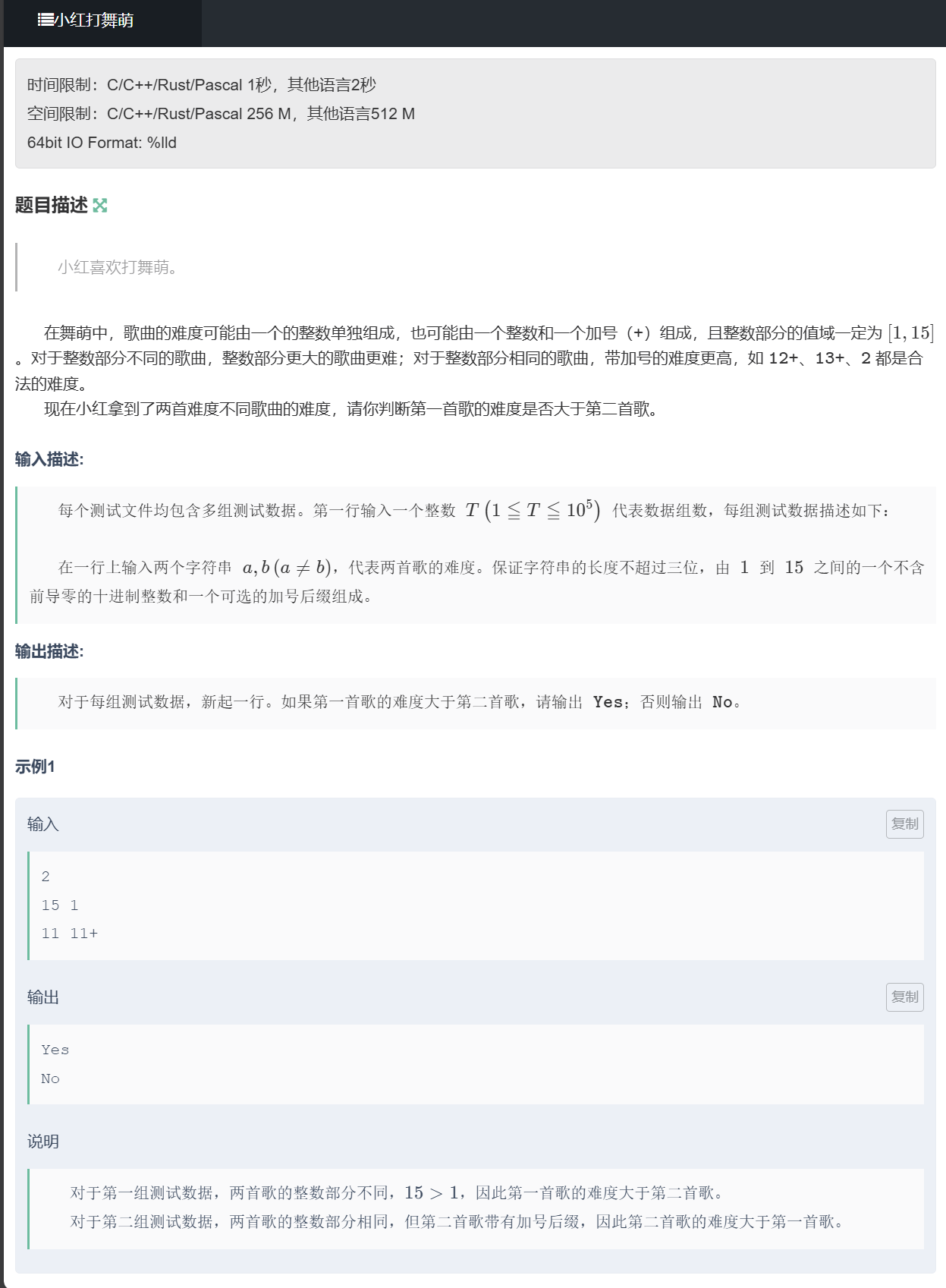
B、小红写谱

题目

思路

  1. 位移量规则

    相邻按键（x,y）的位移为 min(|x-y|, 8-|x-y|)；若x=y，位移直接为0，即相同按键相邻不会增加位移难度。

  2. 相同按键的优化处理

    重排时将相同按键连续放置，这部分的相邻位移均为0，不会影响总位移难度。

  3. 重复次数的无关性

    只需统计"出现过的不同按键"即可------重复次数不影响不同按键的紧凑排列方式，因此不影响最小位移难度的计算。

  4. 位移难度的范围

    题目中的位移难度不包含首尾按键的环形位移，仅计算序列内相邻按键的位移和。

  5. 最优排列的关键

    统计环形键盘上的"最大连续空缺长度"，将其作为首尾按键的衔接间隔，即可确定不同按键的紧凑排列方式，从而得到最小位移难度。

    可以在"最优排列的关键"后补充公式推导 部分，解释7 - mx的由来：

  6. 核心公式推导

    环形键盘总长度为8，我们统计出"未出现按键的最大连续空缺长度"为mx，则出现过的不同按键所占据的连续区间长度 为 8 - mx（环形总长度 - 最大空缺长度）。

    对于连续排列的L个不同按键，其相邻位移之和为 L - 1（例如3个连续按键"1、2、3"，位移和为1+1=2=3-1）。

    将"不同按键的连续区间长度"代入得：位移和 = (8 - mx) - 1 = 7 - mx，这就是最小位移难度的计算公式。

代码

cpp 复制代码 
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void solve()
{
    int n;
    cin >> n;
    vector<int> nums(10); // 标记1-8号按键是否出现,下标0-7对应按键1-8
    for (int i = 1; i <= n; i++) 
    {
        int num;
        cin >> num;
        nums[num - 1] = 1; // 出现过的按键标记为1，重复按键不影响结果
    }
    int mx = 0, cnt = 0;
    // 遍历16次(8*2)，处理环形结构，避免首尾空缺判断
    for (int i = 0; i < 16; i++)
    {
        if (!nums[i % 8]) cnt++; // 当前按键未出现，连续空缺+1
        else cnt = 0;            // 出现按键，重置空缺计数
        mx = max(mx, cnt);       // 更新最大连续空缺长度
    }
    cout << 7 - mx << endl; // 核心公式：求最小位移难度
}
int main() 
{
    ios::sync_with_stdio(0), cin.tie(0); // 加速输入输出
    int m;
    cin >> m;
    while (m--) solve(); // 多组测试用例
    return 0;
}

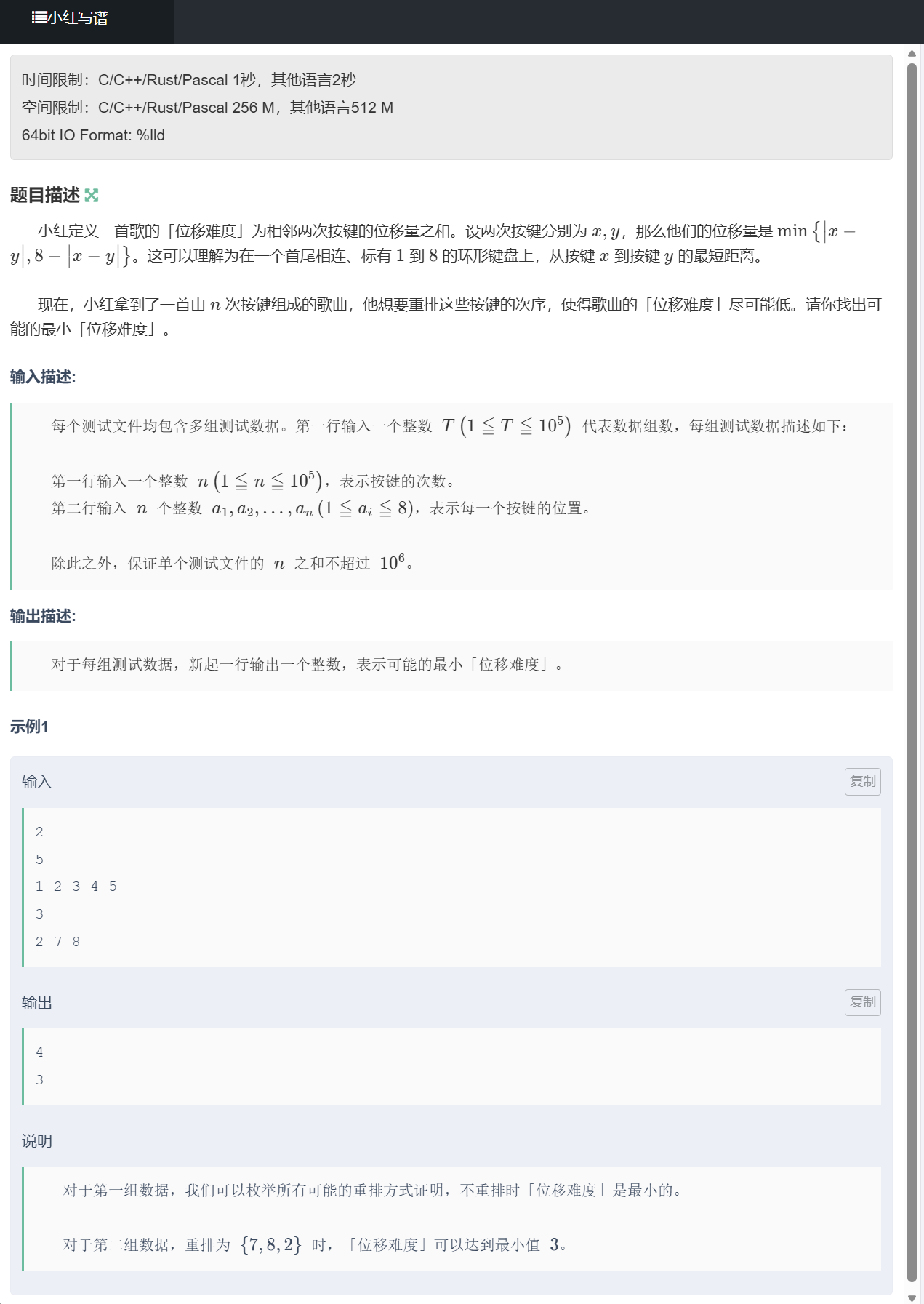
C、小红出勤

题目

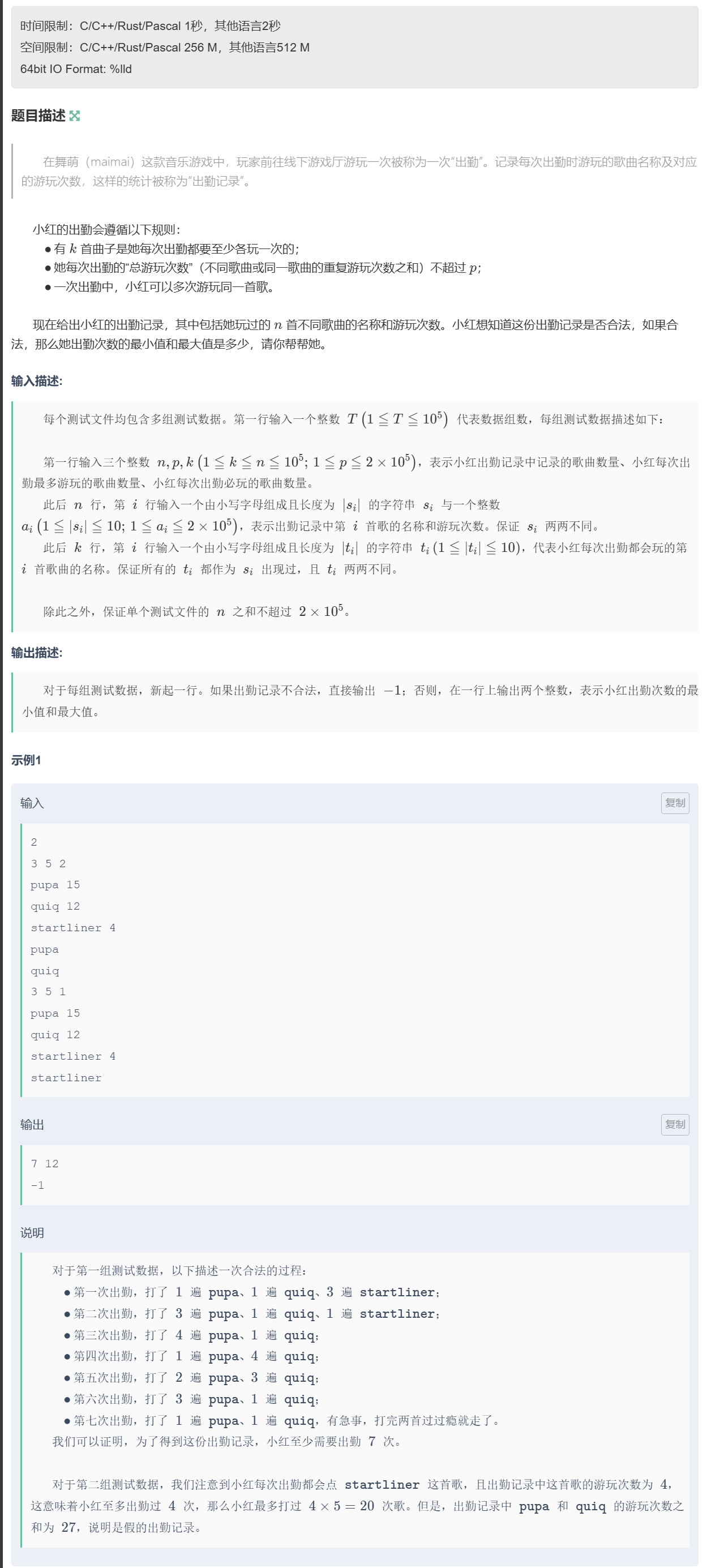
思路

我们可以从题目中推断出游玩测试的范围，最小值为总游玩次数除以每次出勤的最大游玩次数向上取整的结果 （即 ((总游玩次数 + 每次最大游玩次数 - 1) // 每次最大游玩次数)，保证总游玩次数不超过每次出勤的次数限制），最大值为每次出勤必玩歌曲的游玩次数中的最小值 （因为每次出勤必须玩每首必玩歌曲至少1次，出勤次数不能超过任意一首必玩歌曲的游玩次数）。

只有在这个范围内即合理，否则不合理

代码

cpp 复制代码 
#include<iostream>
#include<vector>
#include<unordered_map>
using namespace std;

int main()
{
    int t;
    cin >> t;
    while(t--) // 多组测试用例
    {
        int a, b, c;
        cin >> a >> b >> c; // a:歌曲总数 b:单次最多游玩数 c:必玩歌曲数
        unordered_map<string, int> mp; // 映射：歌曲名 -> 游玩次数
        int num = 0; // 所有歌曲的总游玩次数
        for(int i = 0; i < a; i++)
        {
            string t; int x;
            cin >> t >> x;
            mp[t] = x;
            num += x;
        }
        vector<int> arr;
        for(int i = 0; i < c; i++) // 存入必玩歌曲的游玩次数
        {
            string t; cin >> t;
            arr.push_back(mp[t]);
        }
        if(c > b) // 必玩歌曲数超单次上限，无解
        {
            cout << -1 << endl;
            continue;
        }
        int max1 = 100000;
        for(auto x : arr) max1 = min(max1, x); // 最大出勤次数：必玩歌曲次数最小值
        int min1 = (num + b - 1) / b; // 最小出勤次数：总次数/b 向上取整
        if(min1 > max1) cout << -1 << endl; // 最小需求超最大可能，无解
        else cout << min1 << " " << max1 << endl;
    }
    return 0;
}

D、小红越级（easy）

题目

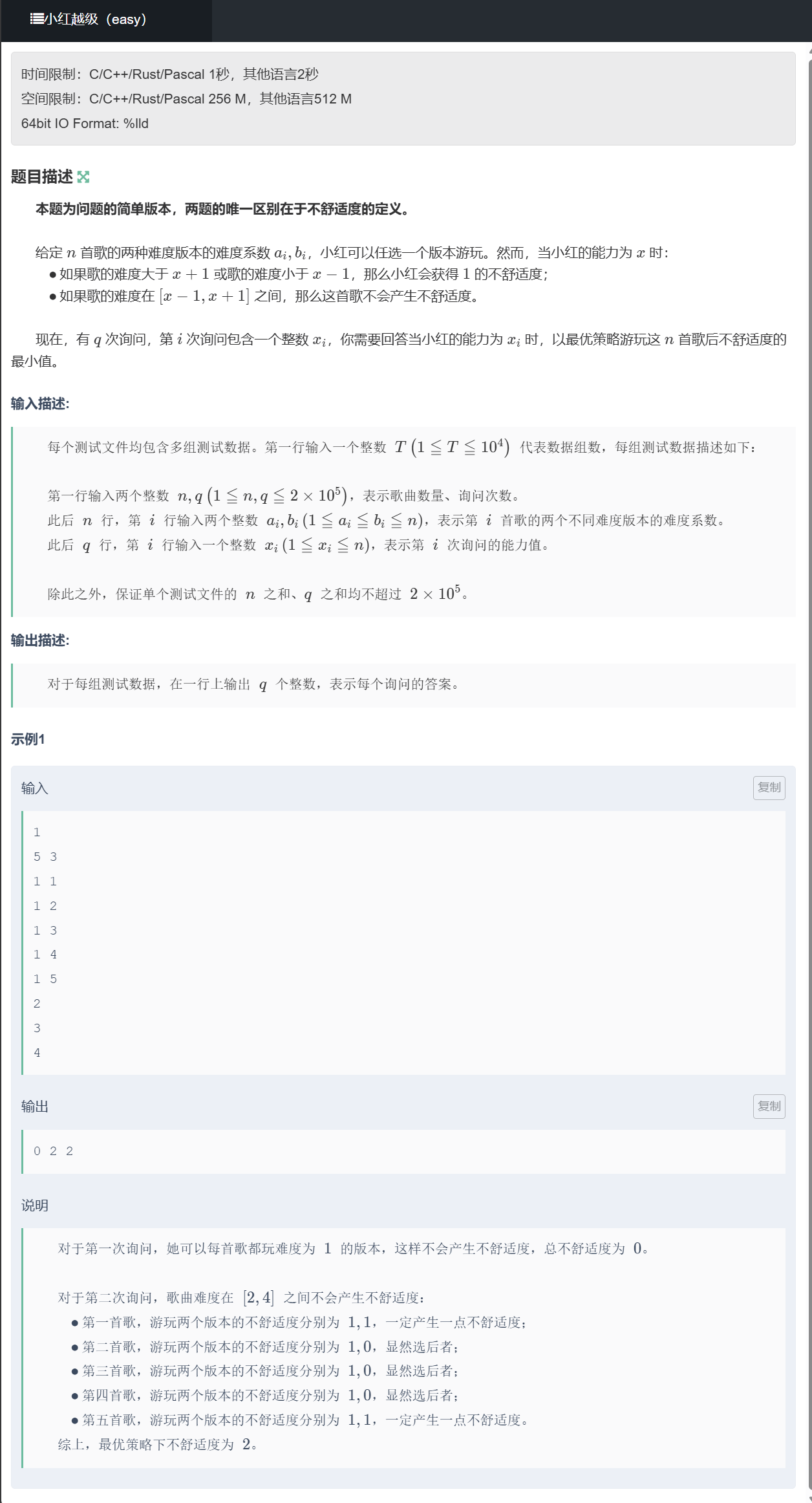
思路

我们由题目可得

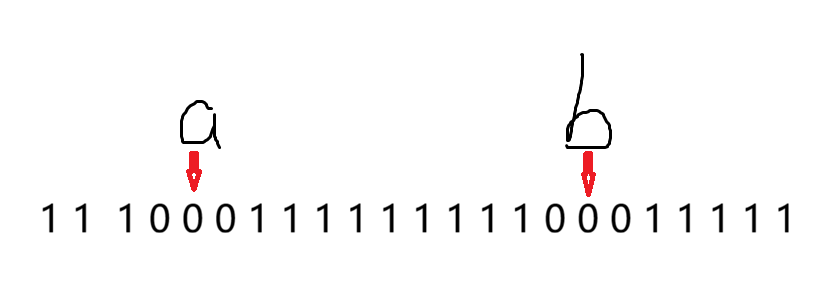
每一首歌都为这种，1为不舒适，0为舒适，每一首歌累加即可，明显的差分问题

代码

cpp 复制代码 
#include<iostream>
#include<vector>
using namespace std;
const int N = 2e5 + 10; // 数据范围上限

int main()
{
	int t;
	cin >> t;
	while (t--) // 多组测试用例
	{
		int n, q;
		cin >> n >> q; // n:歌曲数；q:查询次数
		vector<int>arr(N, 0); // 差分数组：标记"产生不舒适度"的x区间
		
		for (int i = 0; i < n; i++) // 处理每首歌的两个版本a、b
		{
			int a, b; cin >> a >> b; // 歌曲的两个难度版本（a<=b）
			
			// 情况1：x < a-1 → x的舒适区间不包含a/b，标记区间[1, a-1]
			if (a - 2 >= 1) {
				arr[1]++;
				arr[a - 1]--;
			}
			
			// 情况2：x > b+1 → x的舒适区间不包含a/b，标记区间[b+2, n]
			if (b + 2 <= n) {
				arr[b + 2]++;
				arr[n + 1]--;
			}
			
			// 情况3：a+2 ≤x ≤b-2 → x的舒适区间不包含a/b，标记中间区间
			if (a + 2 <= b - 2) {
				arr[a + 2]++;
				arr[b - 1]--;
			}
		}
		
		// 前缀和：计算每个x对应的"最小不舒适度"（即两首版本都不舒适的歌曲数）
		vector<int>crr(N, 0);
		for (int i = 1; i <= n; i++) {
			crr[i] = crr[i - 1] + arr[i];
		}
		
		// 处理查询
		vector<int>brr(q, 0);
		for (int i = 0; i < q; i++) {
			cin >> brr[i]; // 读入查询的能力值x
		}
		// 输出每个查询对应的最小不舒适度
		for (auto i : brr) {
			cout << crr[i] << " ";
		}
		cout << '\n';
	}
	return 0;
}

G、小红越级（hard）

我们这里直接紧接着看最后一题

题目

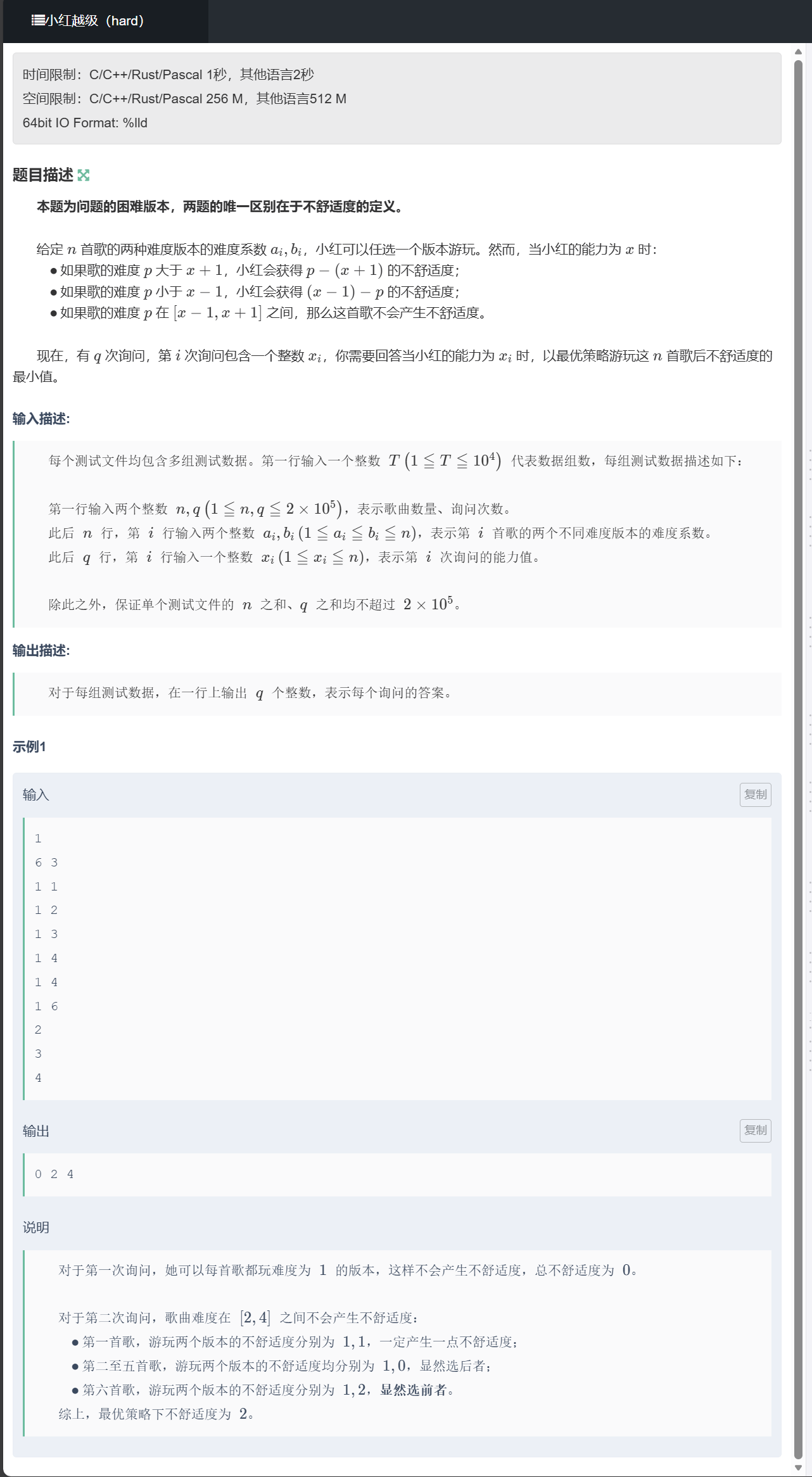
思路

由题目得，与上一题相比，就是把不舒适值改变了，如图

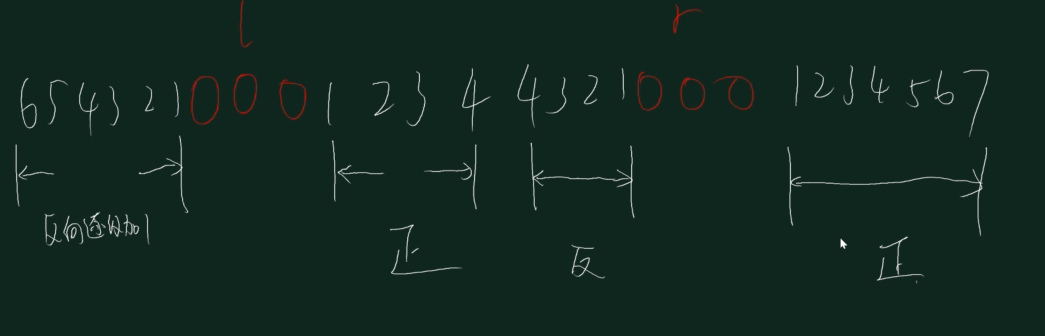
我们还用差分来做

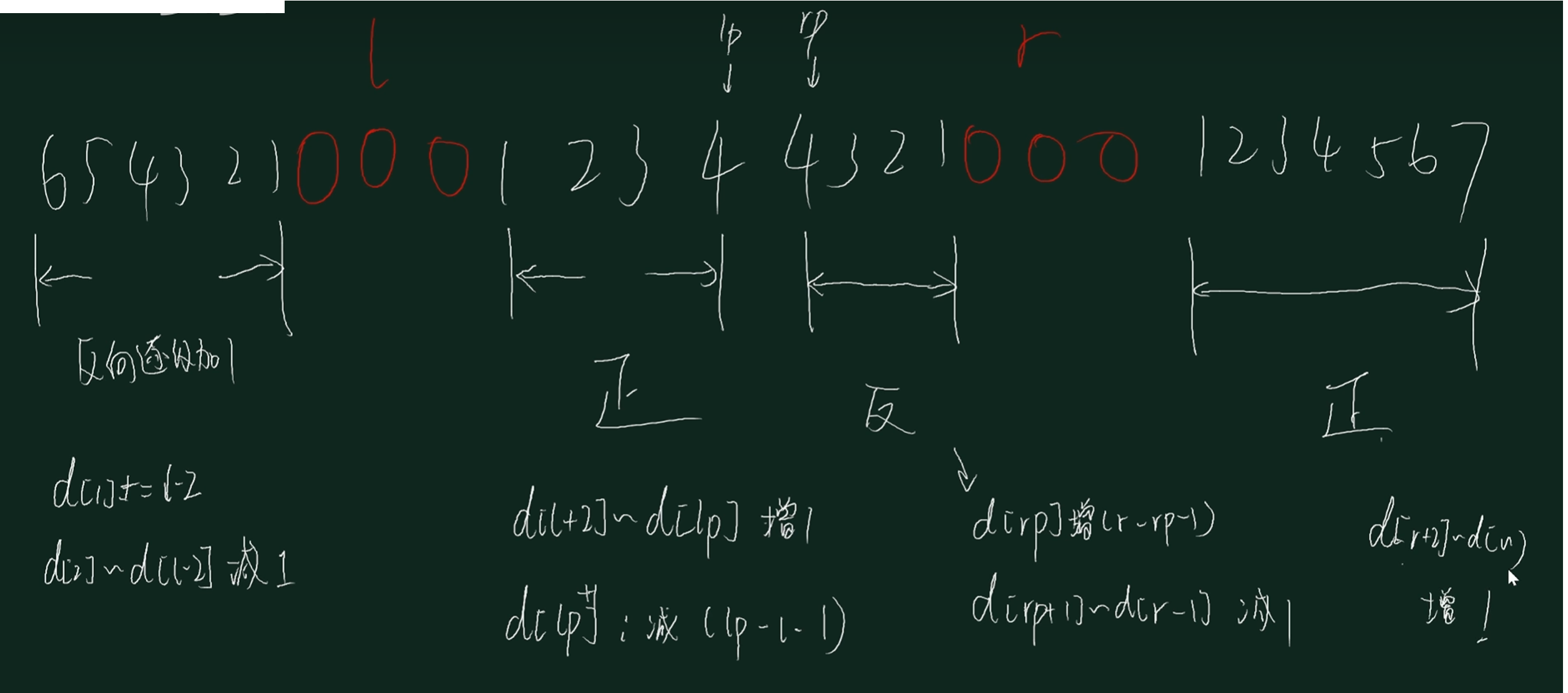
我们发现对于差分数组又出现了比如d[r+2]到d[n]都加一的情况，这时我们可以直接再弄一个差分数组来进行，相当于差分的差分

代码

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
int d[200015];  // 记录每个能力值x的不舒适度基础贡献
int dd[200015]; // 差分数组，维护d的区间增量
int a[200015];  // 前缀和数组，存每个x的最终最小不舒适度

void solve()
{
    int n,q;
    cin>>n>>q;
    // 多组测试，重置数组
    for(int i=1;i<=n;i++) { d[i]=0; dd[i]=0; }

    for(int i=1;i<=n;i++)
    {
        int l,r;
        cin>>l>>r; // 当前歌曲的两个难度版本（l<=r）
        
        // 处理x < l-1的区间：选l的不舒适度贡献，差分维护
        if(l-1>1) {
            d[1] += (l-2); // x=1时的基础贡献
            dd[2]--;       // 差分区间起始标记
            dd[l]++;       // 差分区间结束标记
        }

        // 处理x > r+1的区间：选r的不舒适度贡献，差分维护
        dd[r+2]++;

        // 处理l+1 < x < r-1的中间区间：分两段选l/r更优，差分维护
        if(l < r-2) {
            int lp = (l+r)/2;  // 中间分界点：左段选l，右段选r
            int rp = lp + 1;
            // 左段（l+2到lp）：选l的贡献，差分标记
            dd[l+2]++;
            dd[lp+1]--;
            d[lp+1] -= (lp - l - 1); // 左段基础贡献调整
            // 右段（rp到r-1）：选r的贡献，基础贡献调整
            d[rp] += (r - rp - 1);
            // 右段差分标记
            dd[rp+1]--;
            dd[r]++;
        }
    }

    // 累计差分，更新d的实际贡献
    int plus=0;
    for(int i=1;i<=n;i++) {
        plus += dd[i];
        d[i] += plus;
    }

    // 前缀和计算每个x的最终不舒适度
    for(int i=1;i<=n;i++) {
        a[i] = a[i-1] + d[i];
    }

    // 处理查询，输出对应x的答案
    while(q--) {
        int x; cin>>x;
        cout<<a[x]<<" ";
    }
    cout<<endl;
}

signed main()
{
    int T;
    cin>>T;
    while(T--) solve(); // 多组测试用例
    return 0;
}

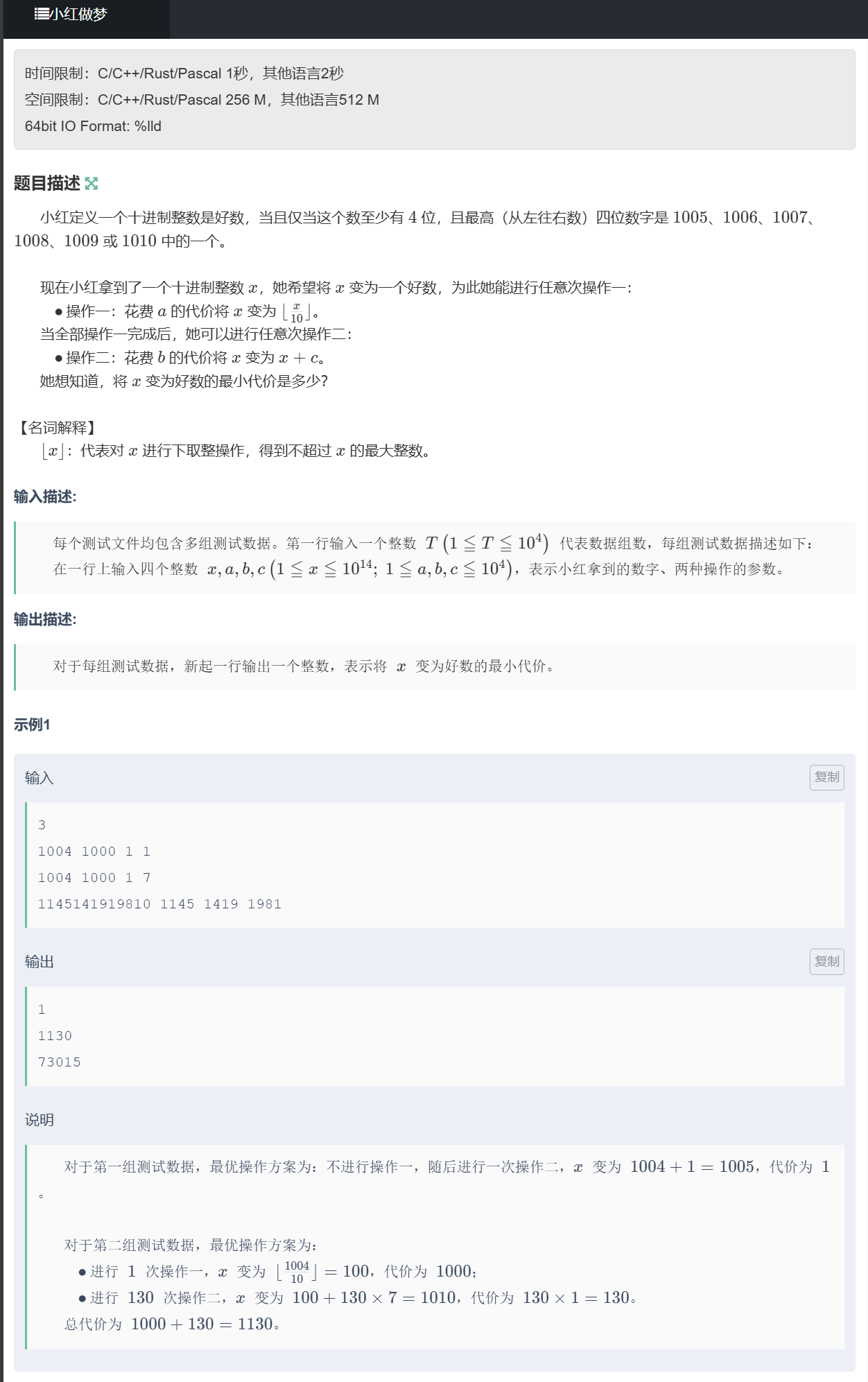
E、小红做梦

题目

思路

题目规定只能「先砍位、后加数」，无后效性。我们枚举所有可能的砍位情况（从砍0位到把x砍成0），对每一个砍位后的数字，利用「好数的固定区间规律」快速计算把它变成好数所需的最少加数次数；最后对每种情况计算「砍位总代价 + 加数总代价」，取所有情况的最小值就是答案。

因为最大14位数，所以我们最多砍15次就行啦

代码

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
#define int long long
// 计算数字 x 通过加 c 变为"好数"所需的最少加法次数
int get_min_add_count(int x, int c) {
    // 好数的起始区间：4位数是[1005, 1010]，5位数是[10050, 10109]，以此类推
    int l = 1005, r = 1010;

    // 我们不断扩大位数（4位, 5位... 直到18位，因为x最大10^16）
    for (int i = 0; i <= 15; ++i) {
        // 如果当前数x已经在这个区间里了，不需要加法
        if (x >= l && x <= r) {
            return 0;
        }

        // 如果x还没达到这个区间的下界，尝试加c补齐
        if (x < l) {
            int k = (l - x + c - 1) / c; // k为达到left_bound至少需要加多少个c（向上取整）
            if (x + k * c <= r) {
                return k; // 补齐后，判断它是否还在这个区间的上界内
            }
        }

        // 更新l、r
        if (i < 15) {
            l *= 10;
            r = r * 10 + 9;
        }
    }
    return 1e18; // 如果实在找不到，返回一个极大值
}

void solve() 
{
    int x, a, b, c;
    cin >> x >> a >> b >> c;
    int ans = 4e18;
    int cut_count = 0;
    // 枚举"砍掉"多少位
    // 注意：即使current_x变成0也可以继续计算，因为可以通过加c变大
    while (1)
    {
        // 计算当前"砍"的代价 + "加"的代价
        int add_k = get_min_add_count(x, c);
        int current_cost = cut_count * a + add_k * b;
        ans = min(ans, current_cost);
        if (x == 0) break;
        x /= 10;        // 砍掉最后一位
        cut_count++;
    }
    cout << ans << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    cin >> t;
    while (t--) 
    {
        solve();
    }
    return 0;
}

代码中对应步骤：

  1. 枚举砍位情况 ：通过while (1)循环，每次执行x /= 10实现"砍最后一位"，用cut_count记录砍位次数，直到x == 0终止枚举；
  2. 算最少加数次数 ：借助get_min_add_count函数，枚举4位、5位等不同位数的好数区间（如4位[1005,1010]、5位[10050,10109]），用向上取整公式计算进入区间的最少加数次数；
  3. 求最小总代价 ：对每种砍位情况，计算cut_count * a + 加数次数 * b，用ans维护所有情况的最小代价。

F、小红开机厅

题目

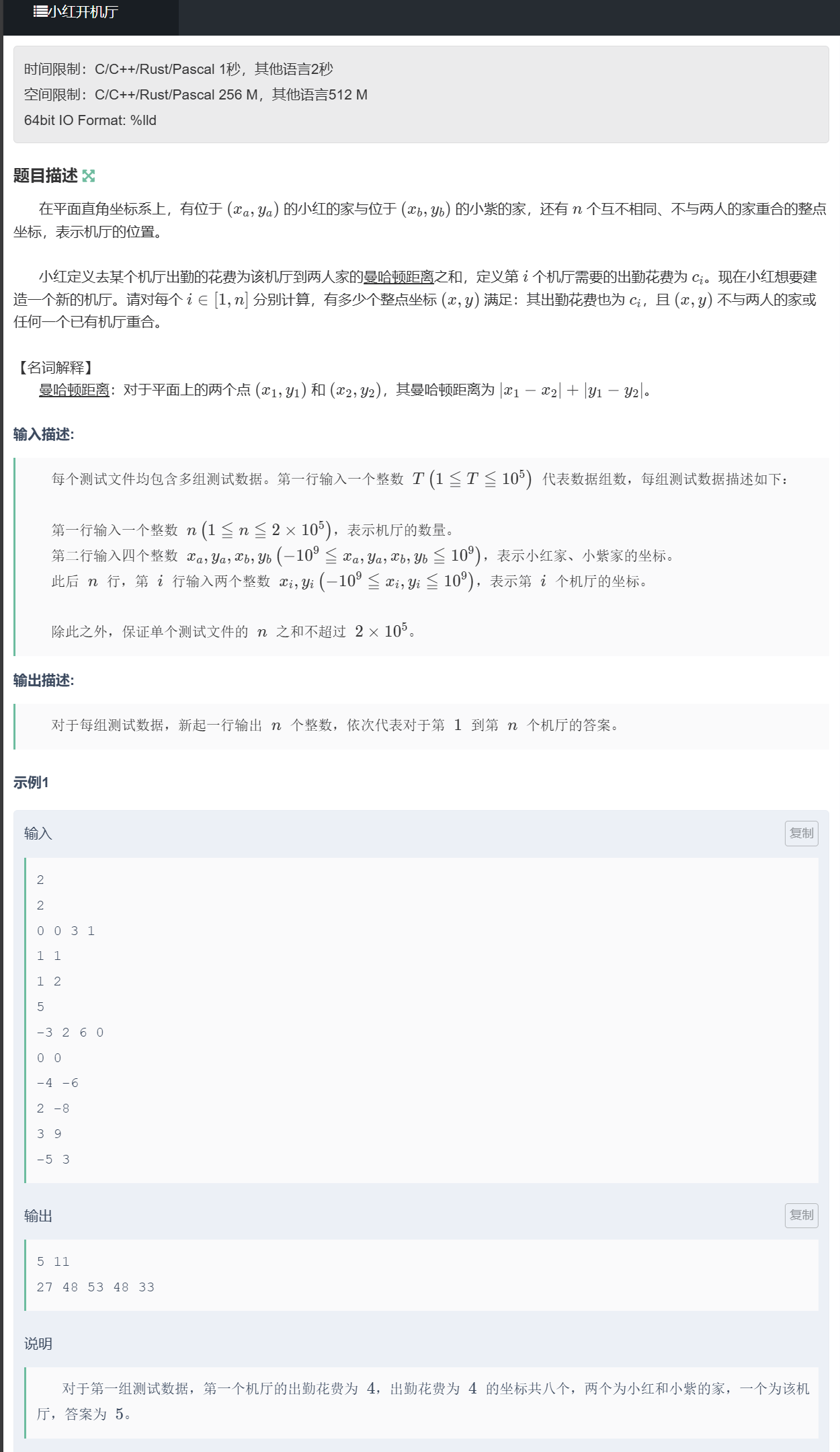
思路

我们通过题目可以分为两种情况

  • 1、机厅在两个家所围成的矩形内

    如图，矩形内所以点到两个家曼哈顿距离之和相等

    这种情况的等距点为边长相乘就是所有符合的机厅

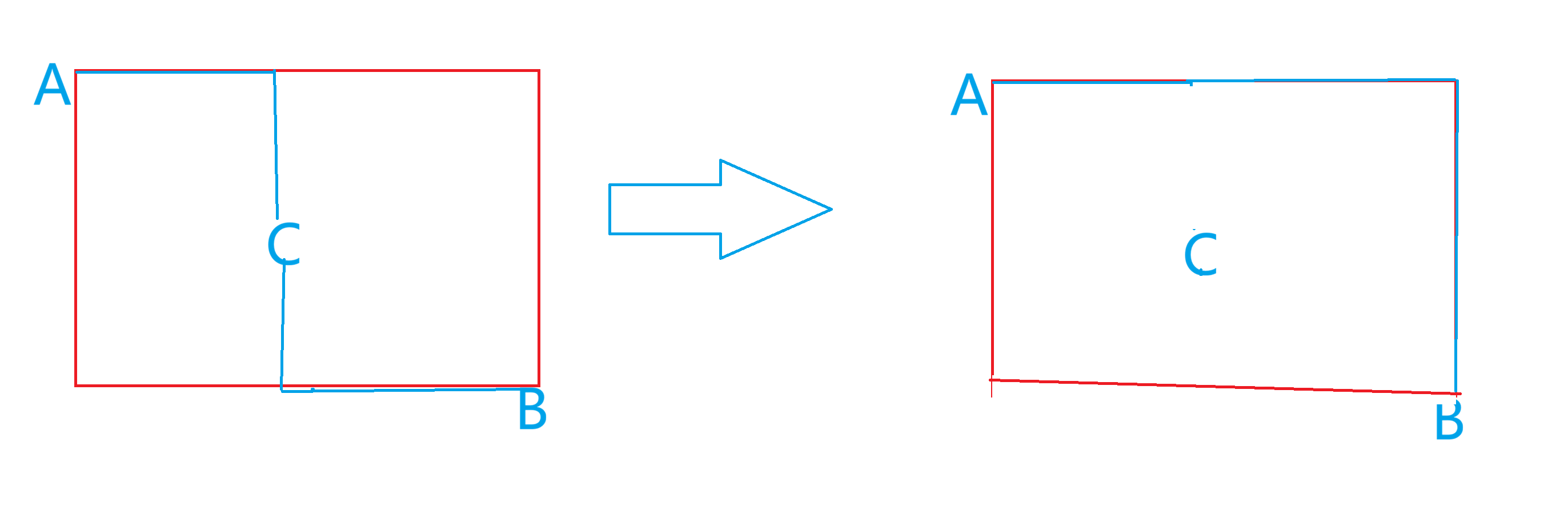
  • 2、机厅在两个家所围成的矩形外

    当点在矩形外时，等距点共有2倍该点至矩形两端点曼哈顿距离

    证明过程：

其中后三种原理

代码

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
int dis[200005];
int n;
void solve() 
{
    unordered_map<int, int> mp;
    cin >> n;
    int xa, ya, xb, yb;
    cin >> xa >> ya >> xb >> yb;
    int X = abs(xa - xb), Y = abs(ya - yb);
    int L = abs(xa - xb) + abs(ya - yb); // 两家之间的曼哈顿距离
    // 记录两家是否重合，若重合，在 K=L 时只占据 1 个位置
    int home_count = (xa == xb && ya == yb) ? 1 : 2;

    for (int i = 0; i < n; ++i) 
    {
        int xi, yi;
        cin >> xi >> yi;
        // 当前机厅到两家的距离之和
        dis[i] = abs(xi - xa) + abs(yi - ya) + abs(xi - xb) + abs(yi - yb);
        mp[dis[i]]++; // 记录该距离出现了多少次
    }

    for (int i = 0; i < n; ++i) 
    {
        int K = dis[i];
        int ans = 0;
        if (K == L) 
        { // 情况 A: 点在矩形内
            ans = (X + 1) * (Y + 1) - home_count;
        } else 
        { // 情况 B: 点在矩形外
            ans = 2 * K;
        }
        ans -= mp[K]; // 排除所有在该距离上的已有机厅
        cout << ans << " ";
    }
    cout << endl;
}

signed main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int t;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

结束语

本文到这里就结束啦！感谢大家的支持，我会持续分享哒！祝大家元旦快乐，新年快乐呀！感谢大家的支持啦！ヾ(◍°∇°◍)ﾉﾞ

相关推荐
leoufung2 小时前
动态规划DP 自我提问模板
算法·动态规划
fqbqrr2 小时前
2601,链式调用
c++
爱编程的小吴2 小时前
【力扣练习题】热题100道【哈希】560. 和为 K 的子数组
算法·leetcode·哈希算法
じ☆冷颜〃2 小时前
基于多数据结构融合的密码学性能增强框架
数据结构·经验分享·笔记·python·密码学
无所事事的海绵宝宝2 小时前
python基础
开发语言·python
Swift社区2 小时前
LeetCode 463 - 岛屿的周长
算法·leetcode·职场和发展
皮卡蛋炒饭.2 小时前
宽搜bfs与深搜dfs
算法·宽度优先
yuuki2332332 小时前
【C++】掌握list：C++链表容器的核心奥秘
c++·后端·链表·list
Coder_Boy_2 小时前
基于SpringAI的智能AIOps项目：部署相关容器化部署管理技术图解版
人工智能·spring boot·算法·贪心算法·aiops
热门推荐
01GitHub 镜像站点02Linux下V2Ray安装配置指南03jdk21下载、安装（Windows、Linux、macOS）04Claude Code Skills 实用使用手册05手把手教你通过Gemini3 pro 学生认证，白用一年，手慢无！06UV安装并设置国内源072025 最新教程：注册并切换到美区 Apple ID08从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击09【踩坑笔记】50系显卡适配的 PyTorch 安装10祝大家 2026 年新年快乐，代码无 bug，需求一次过