深度学习——Logistic回归中的梯度下降法

4.5 梯度下降法

损失函数是衡量单一训练样例的效果，成本函数用于衡量w和b的效果，在全部训练集上衡量。下面我们讨论如何使用梯度下降法（the gradient descent algorithm）去训练或者学习训练集上的参数w和b。

下面是熟悉的logistic回归算法，第二行是成本函数，定义为平均值。即1/m的损失函数之和。损失函数可以衡量算法的效果。每一个训练样例，都输出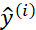，把它和基本真值标签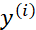进行比较，等号右边是完整的公式。

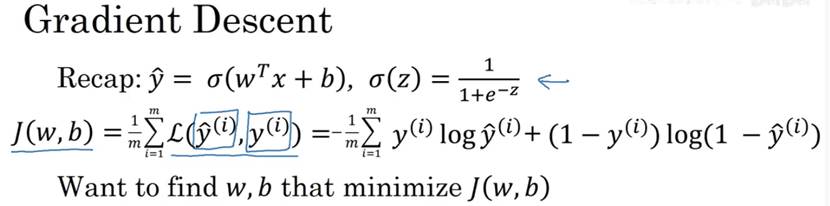
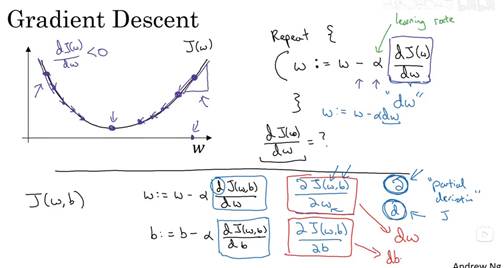
成本函数衡量了参数w和b在训练集（training set）上的效果，要学习到合适的参数w和b，即为使得成本函数尽可能小的w和b，下面是梯度算法介绍。横轴表示参数w和b，实际上，w可以是更高维的，为了方便绘图，w和b都是一个实数。成本函数是在水平轴w和b上的曲面，曲面的高度代表J(w,b)在某一点的值，我们需要找到w和b使得对应的成本函数最小，可以看到成本函数J(w,b)是一个凸函数，像一个碗。为了找到更好的w和b，我们要做的就是用某初始化的w和b（在图中表示为小红点），对于logistic回归来说，几乎任意初始化都是有效的，通常是0。梯度下降法就是从初始的点开始，朝着最抖得下坡方向走一步，在梯度下降一步后或许在那里停下，这是梯度下降的一次迭代，两次迭代或许会抵达那里。这张图片阐述了梯度下降法。

让我们来看一些函数，你希望得到最小化的J(w)，函数可能如下图，为了方便，先忽略b，用一维曲线代替多维，梯度下降法的步骤是：重复执行以下的更新操作，我们更新w的值，用:=来表示更新w。在算法收敛前，重复这样去做。α 表示学习率，学习率可以控制每一次迭代或者梯度下降法中的步长。之后会讨论如何选择α。

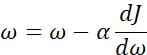
现在w在初始值位置（右侧最高点），对应成本函数J(w)在曲线上的一点，导数的定义是曲线在这一点的斜率，这里导数是正的，新的w值等于w减去学习率乘以导数，因此w接着向左走一步。算法使得w渐渐减小。反之，如果w在左侧最高点，此时导数是负的，w值等于w减去学习率乘以导数，w就会渐渐增大。无论w在哪里，梯度下降法会朝着全局最小值方向移动。

当前J(w)的梯度下降法，只有参数w，在logistic回归算法中，成本函数是一个含有w和b的函数，此时，梯度下降执行以下两个式子更新w和b。在编写代码时，dJ/dω 用dω 表示，dJ/db 用db表示。

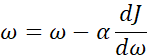
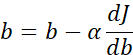
另外，想要明确一下在微积分的符号约定中，dJ/dω 表示为αJ/αω ，当J有两个以上的变量时，使用α 来代表偏导数符号。使用α 还是d取决于函数的变量个数。

4.6 计算图

在这里举一个比logistic回归更简单的神经网络的例子。J是a,b,c的函数：

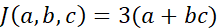
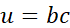
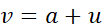
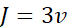
有三个步骤，计算u=bc ，计算v=a+u ，计算J=3v 。可以画成如下流程图，举个例子，对a,b,c 赋值为5，3，2，此时J=33。可以看到这样一个从左到右的流程可以计算出 J。

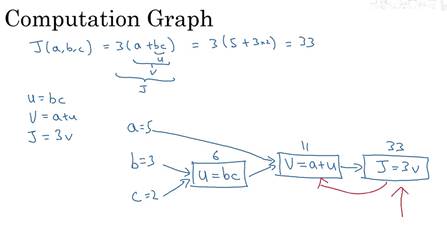
下图为整理后的计算图，通过反向传播算法计算导数 ，实际上核心就是链式传播法则，这里吴恩达老师的视频讲的比较基础。

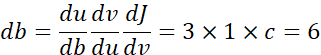
4.7 logistic回归中的梯度下降法

回顾一下logistic回归中的损失函数，现在只考虑单个样本，关于该样本的损失函数定义如下，a 是logistic回归的输出，y是真值标签值（ground truth label），写在写出该样本的偏导数流程图，假设样本只有两个特征x1和x2，为了计算z，我们需要输入参数w1、w2和b。然后，计算。最后计算。

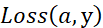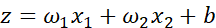
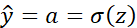
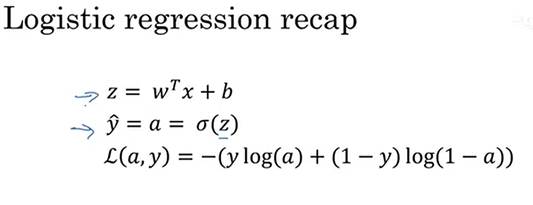
在logistic回归中，我们要做的是，变换参数w和b的值，来最小化损失函数，在前面我们已经通过前向传播步骤，在单个样本上计算损失函数。现在让我们讨论如何反向传播计算偏导数。下面是计算图。

如果想要计算损失函数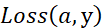的导数，首先要向前一步，计算损失函数关于a 的导数，在代码中，使用da 来表示这个变量，现在进一步计算dz ，损失函数关于dz的导数。最后一步，计算关于w1、w2和b的导数

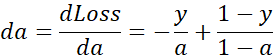
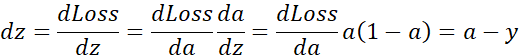
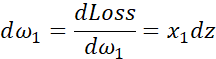
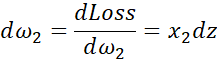
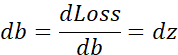
最后，更新w和b：

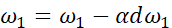
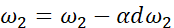
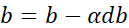
4.9 m个样本的梯度下降

之前我们讲解了在单个训练样本下实现逻辑回归的梯度下降，现在我们需要在m个训练样本上实现梯度下降。回顾一下代价函数的定义，对于代价函数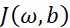，关心的是平均值。

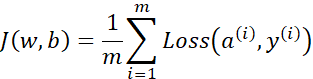
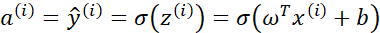
上一小节我们学习了只有一个训练样本的时候如何计算导数，我们可以得到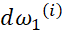、、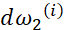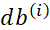，但只是用一个训练样本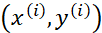，总代价函数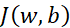对于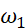的偏导数，也是对于单个样本的损失对 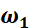求偏导求和再求平均值。

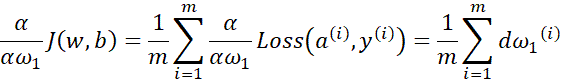
初始化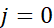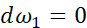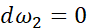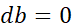，，，；计算每个训练样本的导数，然后把它们相加，假设只有两个特征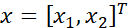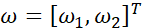，，那么对于m个训练样本，:

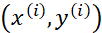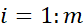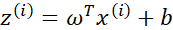
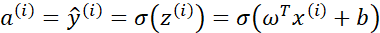
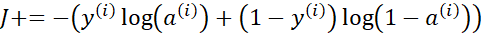
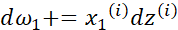
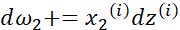
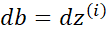
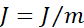
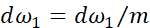
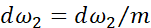
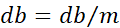
这样就求得了代价函数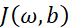对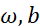的偏导。下面的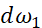、、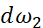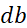没有上标，它们是在整个训练集中的总和。接下来实现更新的步骤。

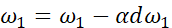
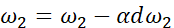
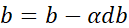
用这种方法实现逻辑回归有两个问题，首先需要写两重循环，第一个for循环是用在m个样本上循环的，第二个for循环是计算这里所有的特征，在这里只有两个特征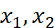，所以只需要写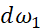、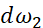，但是如果有n个特征，就是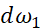、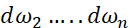，用一个for循环计算这n个特征。这会降低算法的运算效率。在深度学习领域，数据集很大，可以使用矢量化来避免代码中的for循环。