💡 Mini-Batch 梯度下降是现代深度学习中最常用的优化方法。它结合了批量梯度下降的稳定性和随机梯度下降的速度优势。
✅ 一、背景知识:三种梯度下降对比
| 方法 | 样本使用方式 | 优点 | 缺点 |
|---|---|---|---|
| Batch GD | 使用全部样本 | 收敛路径平滑,计算精确 | 内存需求大,速度慢 |
| Stochastic GD | 每次用一个样本 | 内存小,更新快 | 路径震荡剧烈,收敛不稳定 |
| Mini-Batch GD | 每次用一小批样本(如 64) | 平衡速度与稳定性 | 需要选择合适的 batch size |
🔍 核心思想 :
在每一轮迭代中,将训练集分成若干个"mini-batch",依次对每个 mini-batch 计算梯度并更新参数。
✅ 二、Mini-Batch 的实现流程
2.1 步骤分解
- 洗牌(Shuffle):打乱训练数据顺序,防止模型学到数据顺序;
- 分割(Split) :将洗牌后的数据按
mini_batch_size划分为多个子集; - 遍历训练:对每个 mini-batch 执行前向传播 → 反向传播 → 参数更新。
2.2 代码实现详解
def random_mini_batches(X, Y, mini_batch_size=64, seed=0):
np.random.seed(seed)
m = X.shape[1] # 样本数量
mini_batches = []
# 第一步:洗牌
permutation = list(np.random.permutation(m)) # 生成随机索引序列
shuffled_X = X[:, permutation] # 按索引重排 X
shuffled_Y = Y[:, permutation].reshape((1, m)) # 重排 Y 并保持形状
# 第二步:分割
num_complete_minibatches = math.floor(m / mini_batch_size) # 完整批次数
for k in range(0, num_complete_minibatches):
mini_batch_X = shuffled_X[:, k*mini_batch_size:(k+1)*mini_batch_size]
mini_batch_Y = shuffled_Y[:, k*mini_batch_size:(k+1)*mini_batch_size]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# 处理最后一个不完整的 mini-batch
if m % mini_batch_size != 0:
mini_batch_X = shuffled_X[:, num_complete_minibatches*mini_batch_size:]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches*mini_batch_size:]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches✅ 关键点:
permutation确保每次洗牌不同;shuffled_X[:, permutation]实现列重排;- 最后一个 batch 可能小于
mini_batch_size,需单独处理。
2.3 示例输出
X_assess, Y_assess, mini_batch_size = random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess, Y_assess, mini_batch_size)
print("第一个mini_batch_X的维度: " + str(mini_batches[0][0].shape))
print("第二个mini_batch_X的维度: " + str(mini_batches[1][0].shape))
print("第三个mini_batch_X的维度: " + str(mini_batches[2][0].shape))
print("第一个mini_batch_Y的维度: " + str(mini_batches[0][1].shape))
print("第二个mini_batch_Y的维度: " + str(mini_batches[1][1].shape))
print("第三个mini_batch_Y的维度: " + str(mini_batches[2][1].shape))输出示例:
第一个mini_batch_X的维度: (12288, 64)
第二个mini_batch_X的维度: (12288, 64)
第三个mini_batch_X的维度: (12288, 64)
...✅ 说明:每个 mini-batch 包含 64 个样本,特征维度为 12288(如 CIFAR-10 图像展平后)。
✅ 三、图像解析
图1:Mini-Batch 分割示意
- 将总样本
分成多个大小为 64 的 mini-batch;
- 最后一个可能不足 64 个;
- 每个 mini-batch 是独立的训练单元。
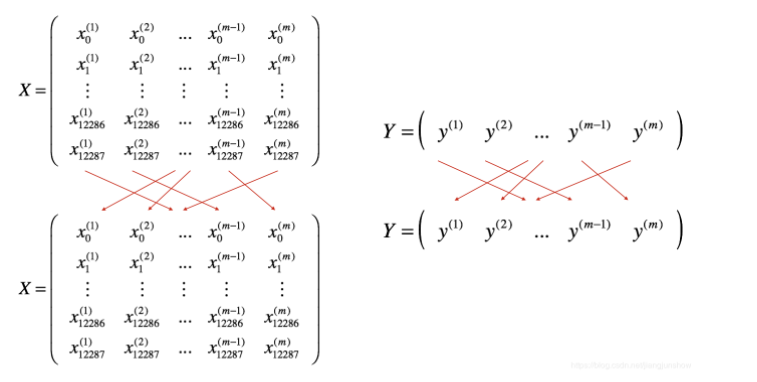
图2:洗牌前后对比

- 上图:原始顺序;
- 下图:随机洗牌后;
- 目的是打破数据相关性,避免模型过拟合顺序模式。
图3:SGD vs Mini-Batch GD 路径对比
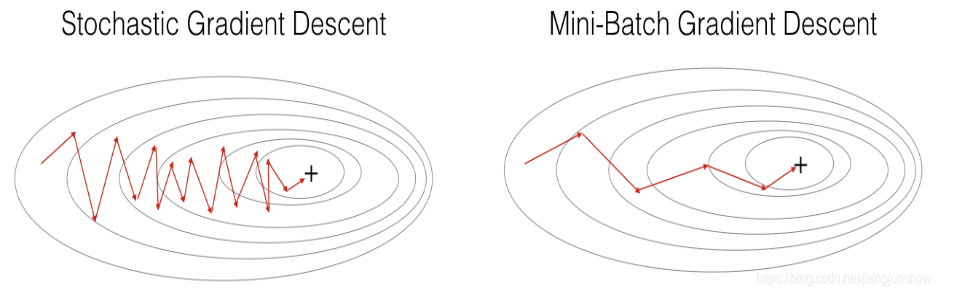
- 左图(SGD):路径跳跃剧烈,噪声大;
- 右图(Mini-Batch GD):路径更平滑,收敛更快且稳定。
✅ 结论:Mini-Batch 在稳定性与效率之间取得最佳平衡。
图4:SGD vs Batch GD 路径对比
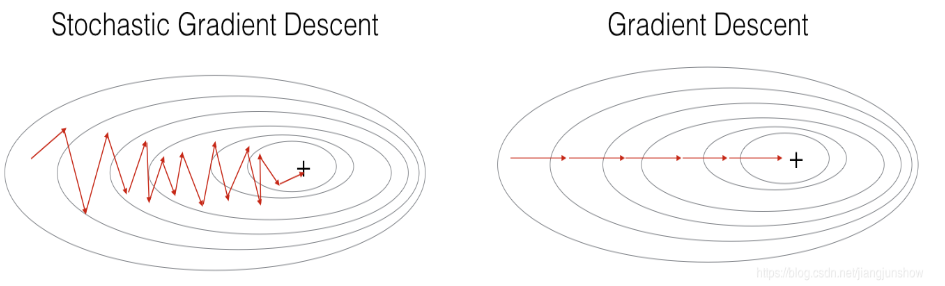
- 左图(SGD):波动大,但能逃出局部极小值;
- 右图(Batch GD):直线前进,但计算成本高。
✅ Mini-Batch 是两者的折衷方案。
✅ 四、Mini-Batch 的完整训练流程
def model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=10000, mini_batch_size=64, print_cost=False):
m = X.shape[1]
parameters = initialize_parameters(layers_dims)
costs = []
for i in range(num_iterations):
# 创建 mini-batches
mini_batches = random_mini_batches(X, Y, mini_batch_size, seed=i)
for mini_batch_X, mini_batch_Y in mini_batches:
# 前向传播
a, caches = forward_propagation(mini_batch_X, parameters)
# 计算损失
cost = compute_cost(a, mini_batch_Y)
# 反向传播
grads = backward_propagation(a, caches, parameters)
# 更新参数
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
if print_cost and i % 1000 == 0:
cost = compute_cost(forward_propagation(X, parameters)[0], Y)
costs.append(cost)
print("Cost after iteration {}: {}".format(i, cost))
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters✅ 特点:
- 每次更新基于一个小批量;
- 减少了内存占用;
- 提升了训练速度;
- 收敛更平稳。
✅ 五、Mini-Batch Size 的选择建议
| Batch Size | 特点 | 适用场景 |
|---|---|---|
| 1 | SGD | 小数据集,快速实验 |
| 32~64 | 推荐范围 | 绝大多数任务 |
| 128~256 | 更稳定 | GPU 显存充足时 |
| 过大(>1024) | 类似 Batch GD | 数据量极大时 |
💡 经验法则:
- 如果显存允许,优先选 64 或 128;
- 小于 32 会增加方差;
- 大于 256 可能导致收敛变慢。
✅ 六、总结:为什么 Mini-Batch 是主流?
| 优势 | 解释 |
|---|---|
| 速度快 | 不需要等待所有样本处理完即可更新参数 |
| 内存友好 | 每次只加载一部分数据 |
| 收敛稳定 | 比 SGD 更平滑,比 Batch GD 更快 |
| 支持并行计算 | GPU 可同时处理整个 mini-batch |