LLama3架构原理浅浅学学

文章目录

说明
[一 LLama3架构](#一 LLama3架构)
[二 Embedding层](#二 Embedding层)
- [2.1 LLama3架构中的Embedding层](#2.1 LLama3架构中的Embedding层)
- [2.2 LLama3中的独特架构---Embedding权重共享](#2.2 LLama3中的独特架构—Embedding权重共享)
- - [2.2.1 回顾Transformer 中的"双塔"结构](#2.2.1 回顾Transformer 中的“双塔”结构)
  - [2.2.2 Llama 3 的"独木桥"设计------权重共享](#2.2.2 Llama 3 的“独木桥”设计——权重共享)
  - [2.2.3 权值共享的优势](#2.2.3 权值共享的优势)
  - [2.2.4 具体案例演示](#2.2.4 具体案例演示)
  - - [2.2.4.1 第一步：定义计算所需的模拟矩阵](#2.2.4.1 第一步：定义计算所需的模拟矩阵)
    - [2.2.4.2 第二步：Llama 3 的输出层计算（权重共享）](#2.2.4.2 第二步：Llama 3 的输出层计算（权重共享）)
    - [2.2.4.3 第三步：对比标准 Transformer（无权重共享）](#2.2.4.3 第三步：对比标准 Transformer（无权重共享）)
  - [2.2.5 总结与回顾](#2.2.5 总结与回顾)
- [2.3 Pytorch代码实现Embedding层](#2.3 Pytorch代码实现Embedding层)
- [2.5 embedding层语义的产生](#2.5 embedding层语义的产生)
- - [2.5.1 阶段一：混沌初开 ------ 随机初始化](#2.5.1 阶段一：混沌初开 —— 随机初始化)
  - [2.5.2 阶段二：演化学习 ------ 在任务中学习语义](#2.5.2 阶段二：演化学习 —— 在任务中学习语义)
  - [2.5.3 语义的涌现：一个可视化的比喻](#2.5.3 语义的涌现：一个可视化的比喻)
  - [2.5.4 结论](#2.5.4 结论)
[三 RMSNorm均方根归一化](#三 RMSNorm均方根归一化)
- [3.1 Layer Normalization与Batch Normalization](#3.1 Layer Normalization与Batch Normalization)
- [3.2 RMSNorm](#3.2 RMSNorm)
- - [3.2.1 RMSNorm公式说明与特点](#3.2.1 RMSNorm公式说明与特点)
  - [3.2.2 Pytorch代码实现RMSNorm](#3.2.2 Pytorch代码实现RMSNorm)
[3.3 旋转位置编码(RoPE)](#3.3 旋转位置编码(RoPE))
- [3.4 旋转位置编码的具体流程](#3.4 旋转位置编码的具体流程)
- [3.5 RoPE（旋转位置编码）核心内容](#3.5 RoPE（旋转位置编码）核心内容)
- [3.6 旋转位置编码的理解](#3.6 旋转位置编码的理解)
- - [3.6.1 从笛卡尔坐标到极坐标：理解旋转的本质](#3.6.1 从笛卡尔坐标到极坐标：理解旋转的本质)
  - [3.6.2 RoPE如何应用旋转：从二维到高维](#3.6.2 RoPE如何应用旋转：从二维到高维)
  - [3.6.3 极坐标视角下的RoPE公式](#3.6.3 极坐标视角下的RoPE公式)
- [3.7 RoPE代码实现(Pytorch风格)](#3.7 RoPE代码实现(Pytorch风格))
- [3.8 旋转位置编码仅应用Q和K矩阵的理解](#3.8 旋转位置编码仅应用Q和K矩阵的理解)
- - [3.8.1 Q、K矩阵与相对位置编码的关联](#3.8.1 Q、K矩阵与相对位置编码的关联)
  - [3.8.2 RoPE不应用于V矩阵的解释](#3.8.2 RoPE不应用于V矩阵的解释)
  - [3.8.3 位置编码的内推和外推](#3.8.3 位置编码的内推和外推)
[四 LLama中的注意力机制与KV缓存](#四 LLama中的注意力机制与KV缓存)
- [4.1 KV缓存机制的工作原理](#4.1 KV缓存机制的工作原理)
- [4.2 KV重复匹配Q代码案例实现](#4.2 KV重复匹配Q代码案例实现)
- [4.3 LLama注意力机制的实现代码](#4.3 LLama注意力机制的实现代码)
[五 LLama中的FFN with SwiGLU](#五 LLama中的FFN with SwiGLU)
- [5.1 FFN with SwiGLU](#5.1 FFN with SwiGLU)
- [5.2 FFN加入混合专家网络](#5.2 FFN加入混合专家网络)
- - [5.2.1 MOE简介](#5.2.1 MOE简介)
  - [5.2.2 MOE训练和推理过程](#5.2.2 MOE训练和推理过程)
  - [5.2.3 MOE瓶颈问题和辅助损失机制](#5.2.3 MOE瓶颈问题和辅助损失机制)
  - [5.2.4 MoE模型的具体实现](#5.2.4 MoE模型的具体实现)
[六 LLama架构小型完整实现](#六 LLama架构小型完整实现)
- [6.1 数据并行与模型并行](#6.1 数据并行与模型并行)
- [6.2 具体的实现代码](#6.2 具体的实现代码)

说明

文中内容学自网络资料，如有错误之处，请在评论区留言，谢谢！
相关部分内容最终著作权归原作者所有，文章内容仅供学习和交流使用。

一 LLama3架构

LLama3（Large Language Model Meta AI）整体结构：LLaMA 7B模型采用典型的Transformer架构变体，包含嵌入层、注意力机制和前馈网络等核心组件，具体是decode-only transformer。

模块组成：

嵌入层(Embeddings)：将输入的离散token转换为连续向量表示。
RMS Norm：替代传统Layer Norm的归一化方法，只计算方差不计算均值。
自注意力机制：采用分组多查询注意力(Grouped Multi-Query Attention)机制。
前馈网络：使用SwiGLU激活函数的Feed Forward结构。
位置编码：采用旋转位置编码(Rotary Positional Encodings)。
注意力机制：分组多查询注意力，通过分组降低计算复杂度，共享部分key-value投影，保留多个查询头(Q)保持表达能力。
- 旋转位置编码：将位置信息融入注意力计算，相比绝对位置编码具有更好的长度外推性，通过旋转矩阵实现位置感知。
前馈网络：SwiGLU激活，结合Swish和GLU的优点 S w i G L U ( x ) = x σ ( β x ) ⊗ ( W x + b ) SwiGLU(x)=x\sigma(\beta x) \otimes (Wx+b) SwiGLU(x)=xσ(βx)⊗(Wx+b)，相比ReLU能更好地处理负值输入。

二 Embedding层

2.1 LLama3架构中的Embedding层

在LLM中，Embedding层大小的影响参数为num_embeddings和embedding_dim
- num_embeddings：词汇表大小或类别数（如10万）。
- embedding_dim：每个token映射的向量维度（如512或4096）。
Embedding层是占用参数量的，中文场景： v o c a b s i z e × d m o d e l vocab_size \times d_model vocabsize×dmodel（如10万×4096≈4亿参数），如果是小型模型时，如d_model设置为512维时，可以显著减少参数量。
Embedding是具有动态特性的，通过权重矩阵实现语义理解。相较于Word2Vec等静态编码，现代Embedding层通过训练迭代的损失函数动态调整参数，使其根据任务需求和训练过程中的上下文环境调整语义表示。
嵌入层的灵活应用，任务适应性：
- 情感分析任务：侧重编码情感特征
- 知识图谱任务：侧重编码实体关系
- 通用语言模型：编码基础语义特征
实现原理：通过可训练的权重矩阵实现动态调整，权重随损失函数优化而更新。
嵌入层的输入与输出
- 输入格式： ( b a t c h s i z e , s e q l e n ) (batch_size, seq_len) (batchsize,seqlen)的整数张量
- 输出格式： ( b a t c h s i z e , s e q l e n , d m o d e l ) (batch_size,seq_len,d_model) (batchsize,seqlen,dmodel)的浮点张量。

2.2 LLama3中的独特架构---Embedding权重共享

2.2.1 回顾Transformer 中的"双塔"结构

标准 Transformer（比如原始的论文或 BERT）中，处理输入和输出的是两个完全独立的、毫无关联的矩阵。

Embedding 层 (输入层)
- 任务：将离散的 Token ID（比如 "猫" 这个词在词典里是第 528 个词）转换成一个密集的、连续的向量（比如一个 4096 维的向量）。计算机无法直接理解文字，但能很好地进行向量运算。这个向量承载了这个词的"语义信息"。
- 参数矩阵 ：我们称之为 W_embedding。它的形状是 [vocab_size, d_model] 。
  - vocab_size：词典大小，比如 128,256。
  - d_model：模型维度，比如 Llama 3 中的 4096。
- 运算：当输入一个 Token ID i 时，Embedding 层做的就是去 W_embedding 矩阵中，取出第 i 行向量，作为这个词的初始表示。
输出层 (LM Head, Language Model Head)
- 任务：在 Transformer 主体（多层 Attention 和 FFN）处理完所有输入信息后，最后一个位置的输出向量（维度为 d_model）需要被转换回对词典中每一个词的预测概率。模型要预测下一个最可能的词是什么，所以它需要计算出每个词成为下一个词的"得分"。
- 参数矩阵 ：W_output。它的形状是 [d_model, vocab_size]。
- 运算：将最后一个隐藏状态向量 H（维度 [d_model]）与 W_output 矩阵相乘，得到一个维度为 [vocab_size] 的 logits 向量，再经过 Softmax 就变成了概率分布。

标准结构的特点 ：W_embedding 和 W_output 是两个完全独立的矩阵。它们的参数数量加起来是 vocab_size * d_model + d_model * vocab_size = 2 * vocab_size * d_model。这是一个巨大的参数开销！

2.2.2 Llama 3 的"独木桥"设计------权重共享

现在，Llama 3 的工程师们提出了一个非常大胆且聪明的想法：**我们真的需要两座独立的桥吗？一座桥（Embedding）负责从"词的世界"走到"向量世界"，另一座桥负责从"向量世界"走回"词的世界"。这两座桥是不是可以建成同一座，只是方向相反？**这就是权重共享的核心思想。
在 Llama 3 中，我们只保留一个矩阵，通常就是 Embedding 层的矩阵 W_embedding。它的形状依然是 [vocab_size, d_model] 。那么，输出层怎么办呢？输出层直接使用 W_embedding 的转置矩阵 。
- W_embedding 的形状是 [vocab_size, d_model]。它的转置 W_embedding.T 的形状就是 [d_model, vocab_size] 。所以，在 Llama 3 中：W_output = W_embedding.T

2.2.3 权值共享的优势

你可能会问，这看起来像个简单的数学技巧，为什么说它非常独特和重要呢？原因有三点：

极致的参数效率 最直接的好处。我们省掉了一个巨大的参数矩阵。
- 节省的参数量 ：vocab_size * d_model。
- 具体数字 ：以 Llama 3 8B 模型为例，vocab_size 约为 128K，d_model 为 4096。
- 节省的参数量 ≈ 128,000 * 4096 ≈ 5.24 亿个参数！这几乎相当于一个完整的 BERT-Base 模型的参数量了！在模型训练成本高昂的今天，这种节省是革命性的。

优雅的"语义对偶性" 这是更深层次、更哲学层面的原因。它让整个模型的设计变得非常和谐。

Embedding 的本质：是把一个词（符号）映射到高维空间中的一个点（向量）。这个过程是在构建一个"语义坐标系"。
Output 的本质：是根据模型计算出的语义向量，去这个"语义坐标系"里寻找最匹配的那个词（符号）。

如果使用两个独立的矩阵，就相当于：

Embedding 用一套坐标系（比如，直角坐标系）来定位词语。
Output 用另一套完全不同的坐标系（比如，极坐标系）来寻找词语。

这显然是不协调的。模型需要花额外的精力去学习如何在这两套"话语体系"之间进行转换。

而权重共享则保证了："编码"过程和"解码"过程使用的是同一套"语义坐标系"。

这创造了一种完美的对称性：

正向过程 ：Token ID -> 通过 W_embedding -> 语义向量
反向过程 ：语义向量 -> 通过 W_embedding.T -> Token ID 的得分

W_embedding.T 在数学上是 W_embedding 的逆运算（在特定条件下）。这意味着，用于"编码"的变换，其"逆变换"被直接用于"解码"。这强制要求模型构建一个自洽、统一的语义空间。一个好的"编码器"天然就应该是一个好的"解码器"，反之亦然。

良好的正则化效应 在机器学习中，约束往往能带来更好的泛化能力，防止过拟合。
- 权重共享就是一种非常强的约束。它强迫模型只用一个矩阵来完成两个不同的任务。这使得这个矩阵必须学习到更鲁棒、更本质的词义表示，而不能在两个独立的矩阵里分别"钻空子"或"死记硬背"。这就像让一个学生同时学习"中译英"和"英译中"，而不是让两个学生分别只学一个方向。前者往往对语言的理解会更深刻、更透彻。

2.2.4 具体案例演示

为了方便计算和画图，我们把模型尺寸缩小到极致：

词典大小 (vocab_size) : 4 词典是：["我", "爱", "猫", "。"]，对应的 ID 分别是 0, 1, 2, 3。
模型维度 (d_model): 3

场景设定：假设我们的模型收到了输入 "我爱"，现在需要预测下一个词。经过 Transformer 主体（多层 Attention 和 FFN）的计算后，最后一个词 "爱" 对应的隐藏状态向量 H 已经生成。

现在，我们的任务就是把这个 H 向量，通过输出层（LM Head），转换成对词典中每个词的预测得分。

2.2.4.1 第一步：定义计算所需的模拟矩阵

Embedding 矩阵 (W_embedding) ：模型唯一存储的词向量矩阵。它的形状是 [vocab_size, d_model]，也就是 [4, 3]。

bash 复制代码

      d_model(0)  d_model(1)  d_model(2)
      ↓           ↓           ↓
      --------------------------------
我(0) |  1.0        0.2        -0.5
爱(1) | -0.3        0.8         0.1
猫(2) |  0.4        -0.6        0.9
。(3) | -0.7        0.5        -0.2

可视化矩阵图 W_embedding (形状 4x3):

bash 复制代码

      +-----+-----+-----+
      | 1.0 | 0.2 | -0.5|  <-- "我" 的向量
      +-----+-----+-----+
      | -0.3| 0.8 | 0.1 |  <-- "爱" 的向量
      +-----+-----+-----+
      | 0.4 | -0.6| 0.9 |  <-- "猫" 的向量
      +-----+-----+-----+
      | -0.7| 0.5 | -0.2|  <-- "。" 的向量
      +-----+-----+-----+

最后一个隐藏状态向量 (H) ：Transformer 主体处理完 "我爱" 之后，为 "爱" 这个位置生成的上下文感知向量。它的形状是 [d_model]，也就是 [3]。假设 H = [0.5, -0.1, 0.6] 可视化向量 H (形状 3x1):
bash 复制代码
```
      +-----+
      | 0.5 |
      +-----+
      |-0.1 |
      +-----+
      | 0.6 |
      +-----+
```

2.2.4.2 第二步：Llama 3 的输出层计算（权重共享）

在 Llama 3 中，输出层的矩阵 W_output 不是独立学习 的，它直接使用 W_embedding 的转置。

生成输出矩阵 W_output ：W_output = W_embedding.T (转置)

W_embedding 的形状是 [4, 3]。W_output 的形状就是 [3, 4]。可视化矩阵图 W_output (形状 3x4):

bash 复制代码

          我(0)   爱(1)   猫(2)   。(3)
          ↓       ↓       ↓       ↓
      +-------+-------+-------+-------+
      |  1.0  | -0.3  |  0.4  | -0.7  |  <-- 来自 W_embedding 的第 0 列
      +-------+-------+-------+-------+
      |  0.2  |  0.8  | -0.6  |  0.5  |  <-- 来自 W_embedding 的第 1 列
      +-------+-------+-------+-------+
      | -0.5  |  0.1  |  0.9  | -0.2  |  <-- 来自 W_embedding 的第 2 列
      +-------+-------+-------+-------+

W_output 的第一列 [1.0, 0.2, -0.5] 正好是 W_embedding 的第一行（"我"的向量）。W_output 的第二列 [-0.3, 0.8, 0.1] 正好是 W_embedding 的第二行（"爱"的向量），以此类推。

执行矩阵乘法 ：目标是计算 Logits = H.T @ W_output。
- H.T 的形状: [1, 3]
- W_output 的形状: [3, 4]
- Logits 的形状: [1, 4] 这个 [1, 4] 的向量，就代表了词典中 4 个词各自的得分。

计算过程： Logits 向量的每一个元素，都是 H 向量与 W_output 对应列的点积。

logit_我 (预测"我"的得分): H 点积 W_output 的第 1 列
= (0.5 * 1.0) + (-0.1 * 0.2) + (0.6 * -0.5)
= 0.5 - 0.02 - 0.3
= 0.18
logit_爱 (预测"爱"的得分): H 点积 W_output 的第 2 列
= (0.5 * -0.3) + (-0.1 * 0.8) + (0.6 * 0.1)
= -0.15 - 0.08 + 0.06
= -0.17
logit_猫 (预测"猫"的得分): H 点积 W_output 的第 3 列
= (0.5 * 0.4) + (-0.1 * -0.6) + (0.6 * 0.9)
= 0.2 + 0.06 + 0.54
= 0.80
logit_。 (预测"。"的得分): H 点积 W_output 的第 4 列
= (0.5 * -0.7) + (-0.1 * 0.5) + (0.6 * -0.2)
= -0.35 - 0.05 - 0.12
= -0.52

得到最终结果 ：Logits 向量是 [0.18, -0.17, 0.80, -0.52]。这个向量还没有归一化，但我们可以直接看出，0.80 是最大的值 ，它对应的是词典中的 "猫" (ID=2)。所以，模型预测下一个词是 "猫"。如果再经过 Softmax 函数，这个向量会变成概率分布，比如 [0.28, 0.19, 0.45, 0.08]，其中 "猫" 的概率最高。

2.2.4.3 第三步：对比标准 Transformer（无权重共享）

如果用标准 Transformer 的方法，W_output 是一个独立的 [3, 4] 矩阵，里面的参数是随机初始化然后独立学习的。比如它可能是这样：
bash 复制代码
```
      +-------+-------+-------+-------+
      |  0.9  |  0.1  | -0.4  |  0.3  |
      +-------+-------+-------+-------+
      | -0.2  |  0.7  |  0.5  | -0.8  |
      +-------+-------+-------+-------+
      |  0.6  | -0.3  |  0.2  |  0.1  |
      +-------+-------+-------+-------+
```
- 这个矩阵的列向量 [0.9, -0.2, 0.6] 和 W_embedding 中任何一行都没有关系。模型需要额外学习如何将隐藏状态 H 映射到这个新的、独立的"词义空间"中。

2.2.5 总结与回顾

特性	标准 Transformer	Llama 3 (权重共享)
Embedding 矩阵	`W_e` 形状 `[vocab, d_model]`	`W_e` 形状 `[vocab, d_model]`
Output 矩阵	`W_o` 形状 `[d_model, vocab]` (独立)	`W_o` = `W_e.T` 形状 `[d_model, vocab]`
参数量	`2 * vocab * d_model`	`vocab * d_model`
核心优势	灵活性高	1. 参数高效 2. 语义对偶 3. 正则化

所以，当你看到 Llama 3 的输出层直接使用 Embedding 层的转置时，不要仅仅把它看作一个节省参数的技巧。它背后蕴含了一种对语言模型本质的深刻理解："词"与"向量"之间的转换，应该遵循同一套内在的、对称的语义规则。
这个设计现在已经成为了现代大语言模型（如 GPT 系列、PaLM 等）的标准配置，足见其成功和重要性。

2.3 Pytorch代码实现Embedding层

在PyTorch中，nn.Embedding层是用于处理离散数据（如单词或类别）的关键组件，特别常见于自然语言处理（NLP）和推荐系统等任务。它的主要功能是将输入的整数索引映射到连续的高维向量空间中，即将索引转化为嵌入向量。
python 复制代码
```
torch.nn.Embedding(num_embeddings, embedding_dim)
```
num_embeddings：嵌入表的大小，即词汇表的大小或类别数。它定义了有多少个不同的
"离散输入"可以映射到嵌入向量。
embedding_dim：每个离散输入（类别、单词等）将被映射到的连续向量的维度大小。
nn.Embedding的输入通常是整数（类别索引或词汇索引），它会根据输入的索引从一个大小(num_embeddings，embedding_dim)的查找表中检索出相应的嵌入向量。

简单案例体验

python 复制代码

import torch
import torch.nn as nn
# 定义embedding层
embedding = nn.Embedding(10, 3) #(num_embedding, embedding_dim)
# 输入索引
input_indices = torch.tensor([[1,2,3],[4,5,6]])
# 获取嵌入向量
output = embedding(input_indices)
print(embedding.weight)
print(output)

完整案例

python 复制代码

import torch
import torch.nn as nn
from collections import Counter

# 1. 准备语料库和创建词汇表
corpus = [
    "我 爱 猫",
    "猫 爱 我",
    "我 爱 狗",
    "狗 爱 猫",
    "猫 和 狗 是 朋友"
]

# 2. 创建词汇表
def build_vocab(corpus):
    # 统计词频
    word_counts = Counter()
    for sentence in corpus:
        words = sentence.split()
        word_counts.update(words)
    
    # 创建词汇表，按词频排序
    vocab = sorted(word_counts.items(), key=lambda x: x[1], reverse=True)
    
    # 添加特殊token
    # [word for word, count in vocab]列表推导式：遍历旧的 vocab 列表中的每一个元组 (word, count)，并只取出其中的 word 部分，然后组成一个新的列表。
    vocab = ['<PAD>', '<UNK>'] + [word for word, count in vocab]
    
    # 创建词到索引的映射
    word2idx = {word: idx for idx, word in enumerate(vocab)}
    idx2word = {idx: word for word, idx in word2idx.items()}
    return word2idx, idx2word

# 构建词汇表
word2idx, idx2word = build_vocab(corpus)

print("词汇表:")
for word, idx in word2idx.items():
    print(f"'{word}': {idx}")

print(f"\n词汇表大小: {len(word2idx)}")

# 3. 创建分词和索引化函数
def tokenize_and_index(text, word2idx):
    # 分词（简单按空格分割）
    words = text.split()
    # 转换为索引，未知词用<UNK>的索引
    indices = [word2idx.get(word, word2idx['<UNK>']) for word in words]
    return words, indices

# 4. 创建embedding层
embedding_dim = 50  # 使用更大的维度以获得更好的表示
embedding = nn.Embedding(len(word2idx), embedding_dim)

# 5. 处理真实文本
text = "我 爱 猫"
words, indices = tokenize_and_index(text, word2idx)

print(f"\n原始文本: '{text}'")
print(f"分词结果: {words}")
print(f"索引序列: {indices}")

# 转换为tensor
input_indices = torch.tensor([indices])

# 6. 获取embedding 本质为索引操作
output = embedding(input_indices)

print(f"\n输入索引形状: {input_indices.shape}")
print(f"输出embedding形状: {output.shape}")
print(f"输出embedding:\n{output}")

# 7. 查看每个词的具体向量
print("\n每个词的embedding向量:")
for i, word in enumerate(words):
    idx = indices[i]
    vector = embedding.weight[idx].detach().numpy()  # 获取词向量
    print(f"'{word}' (索引 {idx}): {vector[:5]}...")  # 只显示前5维

# 8. 处理多个句子
print("\n" + "="*50)
print("处理多个句子:")

sentences = ["我 爱 猫", "狗 爱 猫", "我 爱 未知词"]

all_indices = []
for sentence in sentences:
    words, indices = tokenize_and_index(sentence, word2idx)
    all_indices.append(indices)
    print(f"'{sentence}' -> {indices}")

# 转换为tensor并获取embedding
batch_indices = torch.tensor(all_indices)
batch_embeddings = embedding(batch_indices)

print(f"\n批量输入形状: {batch_indices.shape}")
print(f"批量输出形状: {batch_embeddings.shape}")

# 9. 计算词之间的相似度（可选） 这里演示计算方法 并无语义信息
# Embedding 向量的语义不是凭空产生的，而是在模型训练过程中，通过一个明确的任务（比如预测下一个词）被"逼迫"学习出来的。
def cosine_similarity(vec1, vec2):
    return torch.cosine_similarity(vec1, vec2, dim=0)

# 获取"我"和"猫"的向量
vec_me = embedding.weight[word2idx['我']]
vec_cat = embedding.weight[word2idx['猫']]
vec_dog = embedding.weight[word2idx['狗']]

print("\n词向量相似度:")
print(f"'我' 和 '猫' 的相似度: {cosine_similarity(vec_me, vec_cat):.4f}")
print(f"'我' 和 '狗' 的相似度: {cosine_similarity(vec_me, vec_dog):.4f}")
print(f"'猫' 和 '狗' 的相似度: {cosine_similarity(vec_cat, vec_dog):.4f}")

bash 复制代码

词汇表:
'<PAD>': 0
'<UNK>': 1
'爱': 2
'猫': 3
'我': 4
'狗': 5
'和': 6
'是': 7
'朋友': 8

词汇表大小: 9

原始文本: '我 爱 猫'
分词结果: ['我', '爱', '猫']
索引序列: [4, 2, 3]

输入索引形状: torch.Size([1, 3])
输出embedding形状: torch.Size([1, 3, 50])
输出embedding:
tensor([[[ 0.0150,  0.9199, -0.8063,  2.0132,  1.0257,  0.0376,  1.5074,
           0.1043, -0.1475, -0.9671, -0.1785,  1.4232, -1.1741,  0.0455,
           1.0734,  0.9916,  1.6958,  1.8884,  1.6577, -1.8457,  0.9332,
           2.2417, -0.5347,  1.4940,  0.9481,  0.6790, -1.8907, -2.0385,
           1.2264,  1.4855, -0.9506, -1.8371,  0.5655, -0.7643, -2.2646,
          -0.9432, -0.2479, -0.6809,  0.1499,  0.6726,  1.1182,  0.8831,
          -1.1536, -0.5136,  1.0629,  1.4173,  0.2109,  1.3292, -0.3266,
          -1.2734],
         [-1.2650,  0.3248, -1.1844,  0.0145,  0.4337, -2.6102, -0.1422,
          -0.1459,  0.4806, -0.1249, -0.9275, -0.3461, -0.3240, -0.9346,
           0.1373, -0.7633, -0.9869, -0.0907,  0.6864, -0.6091, -0.2252,
           0.1744, -0.5908,  1.5640,  0.4244,  1.0076,  2.0054, -0.2510,
           1.1107,  1.2374,  2.0730,  1.6342,  0.3457,  1.4659,  0.8319,
           0.4997,  1.2795, -0.6787,  0.0092, -0.1781,  0.6557, -0.4838,
          -0.7453, -0.5039, -0.0731, -0.8341,  0.5762,  0.5880, -0.7406,
           0.4669],
         [ 0.8240,  1.4085,  1.5154,  1.3351, -1.4219, -0.4674, -0.2720,
           0.4946, -0.3442, -0.4052,  0.7006, -1.1547, -2.1735,  0.9123,
           2.0569, -0.3022, -0.1364,  0.7195, -1.7760,  1.1321, -0.3809,
          -0.2071,  0.2377, -0.7597,  0.3046, -2.8979,  0.7263, -1.1419,
          -0.3352, -0.4719,  0.4337, -0.7829,  1.1989, -0.3139, -0.5337,
           1.2797,  1.7404,  0.8573,  1.6534, -1.3974, -0.8708, -0.7966,
           0.5250, -1.2430,  1.2439,  0.2599,  0.3104,  1.3406, -0.2097,
          -0.9290]]], grad_fn=<EmbeddingBackward0>)

每个词的embedding向量:
'我' (索引 4): [ 0.01500247  0.9199133  -0.8062882   2.0131807   1.0256754 ]...
'爱' (索引 2): [-1.2649922   0.32480013 -1.1843623   0.01449967  0.4337464 ]...
'猫' (索引 3): [ 0.82400215  1.4084941   1.5154138   1.3351161  -1.4219291 ]...

==================================================
处理多个句子:
'我 爱 猫' -> [4, 2, 3]
'狗 爱 猫' -> [5, 2, 3]
'我 爱 未知词' -> [4, 2, 1]

批量输入形状: torch.Size([3, 3])
批量输出形状: torch.Size([3, 3, 50])

词向量相似度:
'我' 和 '猫' 的相似度: -0.0050
'我' 和 '狗' 的相似度: 0.1211
'猫' 和 '狗' 的相似度: 0.0716

2.5 embedding层语义的产生

embedding向量化token不是要考虑语义吗？这里embedding矩阵参数直接随机初始化，然后查询使用，在模型训练中不是不合适吗？

简单来说：Embedding 向量的语义不是凭空产生的，而是在模型训练过程中，通过一个明确的任务（比如预测下一个词）被"逼迫"学习出来的。根据embedding是否具有语义，可以分解成两个阶段："混沌初开" 和 "演化学习"。

2.5.1 阶段一：混沌初开 ------ 随机初始化

在刚刚创建 nn.Embedding 层时，它的权重矩阵确实是随机初始化的。
python 复制代码
```
embedding = nn.Embedding(len(word2idx), embedding_dim)
```

此时：

"猫" 的向量可能是 [0.12, -0.45, 0.78, ...]
"狗" 的向量可能是 [-0.33, 0.91, 0.05, ...]
"爱" 的向量可能是 [0.67, -0.22, 0.44, ...]

这些向量之间没有任何语义关系。"猫"和"狗"的向量在空间中的距离，和"猫"与"汽车"的距离一样，都是随机的。它们只是一堆无意义的数字。

2.5.2 阶段二：演化学习 ------ 在任务中学习语义

真正的魔法发生在模型训练 的过程中。让我们以一个最典型的任务：预测下一个词 为例，看看语义是如何"涌现"的。

设定目标 模型的目标是：给它一句话的前半部分，让它预测后半部分最可能出现的词。
- 输入: "我爱"
- 正确答案: "猫" (假设我们的语料库里这句话的结尾是"猫")

模型的第一次"瞎猜" 模型取出 "我" 和 "爱" 的随机向量。将这两个随机向量送入 Transformer 的后续层（Attention, FFN）。最后，输出层会计算出词典里所有词的概率。由于输入是随机的，输出也基本是瞎猜。它可能会预测下一个词是 "。" (概率 30%)，"狗" (概率 25%)，"猫" (概率 10%)...

计算损失并"惩罚"
- 模型猜 "猫" 的概率只有 10%，但正确答案就是 "猫"。
- 损失函数会计算出一个很大的"错误分数"。模型猜得越离谱，这个分数就越高。

反向传播 这是整个过程中最关键的一步。这个巨大的"错误分数"会像一股电流，从后往前 ，流经模型的每一个部分，包括：Transformer 的所有层。......以及最开始的 Embedding 层！
- 反向传播算法会计算出，为了让下次预测更准确，每一个参数（包括 Embedding 矩阵中的每一个数字）应该朝哪个方向微调，才能让"错误分数"降低一点点。

更新参数 ------ 语义的"塑形" 模型根据反向传播计算出的方向，微调所有参数。现在，聚焦于 Embedding 层：
- "猫" 的向量：因为模型这次没猜中它，所以它的向量会被调整。调整的方向是，如果下次再遇到类似的上下文（比如 "我爱"），它能让模型更容易输出 "猫"。
- "爱" 的向量：因为它作为输入的一部分，导致了预测错误，所以它的向量也会被微调。新的向量需要更好地承载"喜欢"这种语义，以便和"猫"、"狗"等名词建立更强的联系。
- "狗" 的向量：它可能也被调整了。也许因为 "我爱" 这个上下文，模型也提高了对 "狗" 的预测（虽然没猜对），所以 "狗" 的向量可能会被稍微拉向 "爱" 的向量。

2.5.3 语义的涌现：一个可视化的比喻

想象一个巨大的、空旷的房间（高维空间）。

初始状态：你把词典里所有的词（"猫", "狗", "爱", "跑", "汽车"...）都随机扔到房间的各个位置。它们的位置毫无规律。
训练过程 ：你（训练器）不断地给模型下达指令：
- "我看到 '猫' 和 '喵' 经常一起出现，让它们靠近一点！"
- "我看到 '狗' 和 '汪' 经常一起出现，也让它们靠近一点！"
- "我看到 '猫' 和 '狗' 都经常出现在 '宠物' 旁边，让它们三个都靠近一点！"
- "我看到 '汽车' 和 '跑' 的关系，和 '猫' 和 '跑' 的关系不一样，让 '汽车' 离 '跑' 远一点！"
最终状态 ：经过数百万次这样的指令后，房间里的词不再是随机分布了。
- "猫"、"狗"、"宠物" 会聚集在房间的**"宠物区"**。
- "汽车"、"卡车"、"轮子" 会聚集在**"交通工具区"**。
- "爱"、"喜欢"、"讨厌" 会聚集在**"情感区"**。

此时，每个词在房间里的坐标（也它的 Embedding 向量），就天然地包含了它的语义信息！ 相似的词坐标相近，相关的词在空间中存在某种关系。

2.5.4 结论

问题：

embedding向量化token不是要考虑语义吗？这里embedding矩阵参数直接随机初始化，然后查询使用，在模型训练中不是不合适吗？
回答是：不仅合适，而且是必须的。

随机初始化是起点，它给了模型一个"白板"去自由创作，而不是被人类的先验知识所束缚。
训练过程 是画笔，它通过海量的数据和明确的任务，在这张白板上绘制出了精妙绝伦的"语义地图"。
Embedding 的语义，不是被"赋予"的，而是被"学习"出来的。这正是深度学习的魅力所在！

三 RMSNorm均方根归一化

3.1 Layer Normalization与Batch Normalization

Layer Normalization是Transformer中的关键归一化技术。与Batch Normalization（批归一化）不同，Layer Normalization不是对一个批次（batch）中的样本进行归一化，而是独立地对每个样本中的所有特征进行归一化（对单一词向量、单一时间点的所有embedding维度进行归一化）。具体来说，对于每个样本，Layer Normalization会在特定层的所有激活上计算均值和方差，然后用这些统计量来归一化该样本的激活值。
LN和BN的差别：
- Batch Norm：在batch维度统计特定神经元节点的输出分布（跨样本统计）
- Layer Norm：在层维度统计同一样本下所有神经元节点的输出分布（同一样本内统计）
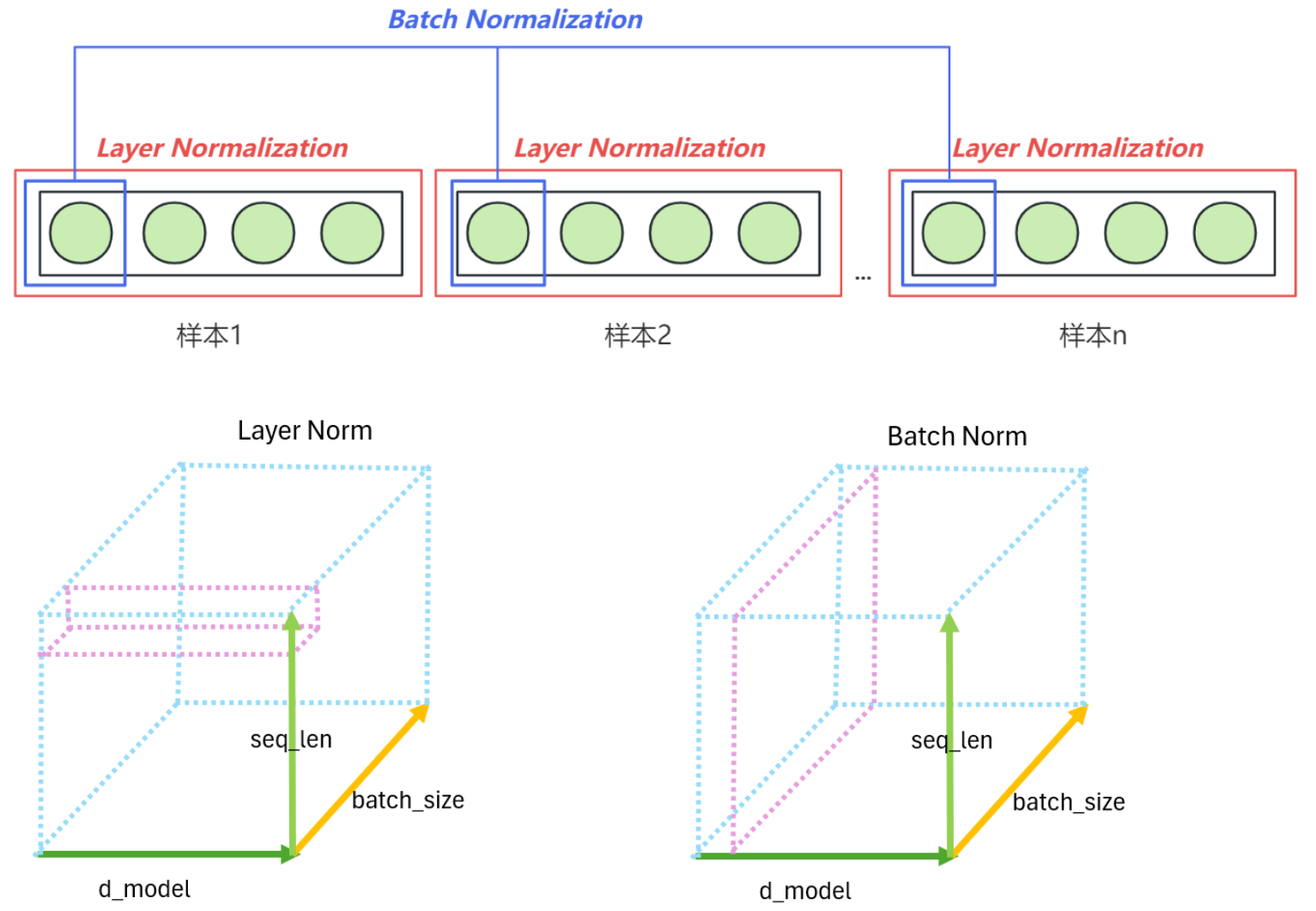
计算方式:
- Batch Norm：纵向计算每个词向量矩阵的第一列均值和方差（如三个词向量矩阵的第一列组成统计面）
- Layer Norm：横向计算每个词向量矩阵的第一行均值和方差（如三个词向量矩阵的第一行组成统计面）
将词向量矩阵视为三维结构时，Batch Norm沿样本轴切片，Layer Norm沿特征轴切片
实际计算时虽然图示只显示单行/列，但操作对象是完整的特征矩阵。
Layer Norm在NLP中应用的优势:
- 处理变长句子时无需考虑batch内其他样本长度差异
- 适用于小batch size场景（当内存受限或需要加速训练时）
- 适配序列元素的逐项处理模式（如自回归生成场景）
- 在Transformer深层结构中有效防止梯度爆炸/消失

3.2 RMSNorm

LayerNorm会对输入特征的均值和方差进行计算，然后用这些统计量对每个特征进行归一化。RMSNorm(Root Mean Square Normalization)只计算输入特征的均方根（RMS，Root Mean Square)，而不考虑均值。因此，RMSNorm去掉了均值的计算，直接利用每个特征的均方根进行归一化，计算量更小。
与传统 LayerNorm 的对比

归一化方法	计算内容	计算复杂度	是否有偏移参数 β \beta β
LayerNorm	均值 + 方差	较高	有（ γ , β \gamma, \beta γ,β）
RMSNorm	仅均方根（RMS）	较低	仅 γ \gamma γ

RMSNorm 省去了计算均值的步骤，减少了约 15% 的计算量，同时在大规模语言模型（如 LLaMA 系列）中，实验证明其性能与 LayerNorm 相当，甚至训练更加稳定。
Llama 3 架构中使用的 RMSNorm（Root Mean Square Layer Normalization）公式如下：
RMSNorm ( x ) = x 1 n ∑ i = 1 n x i 2 + ϵ ⋅ γ \text{RMSNorm}(x) = \frac{x}{\sqrt{\frac{1}{n}\sum_{i=1}^{n} x_i^2 + \epsilon}} \cdot \gamma RMSNorm(x)=n1∑i=1nxi2+ϵ x⋅γ

其中：
- x x x是输入向量（或张量）；
- n n n是输入向量的维度（即特征数量）；
- ϵ \epsilon ϵ是一个极小常数（如 $10^{-6})），用于防止除以零；
- γ \gamma γ是可学习的缩放参数（weight），与输入向量同维度，用于对归一化后的结果进行自适应缩放。

3.2.1 RMSNorm公式说明与特点

均方根计算 ：
RMS ( x ) = 1 n ∑ i = 1 n x i 2 \text{RMS}(x) = \sqrt{\frac{1}{n}\sum_{i=1}^{n} x_i^2} RMS(x)=n1i=1∑nxi2
RMSNorm 仅计算输入向量元素的均方根，不计算均值，因此比传统的 LayerNorm 更高效。
归一化 ：
x ^ = x RMS ( x ) + ϵ \hat{x} = \frac{x}{\text{RMS}(x) + \epsilon} x^=RMS(x)+ϵx
将输入向量除以其均方根，使输入向量的 L2 范数稳定在 n \sqrt{n} n 左右，有助于提升训练稳定性。
可学习缩放 ：
y = x ^ ⋅ γ y = \hat{x} \cdot \gamma y=x^⋅γ
最后乘以可学习的缩放参数 γ \gamma γ，使模型能够自适应调整不同特征维度的重要性。

3.2.2 Pytorch代码实现RMSNorm

Llama 3 架构中使用的 RMSNorm（Root Mean Square Layer Normalization）公式如下：
RMSNorm ( x ) = x 1 n ∑ i = 1 n x i 2 + ϵ ⋅ γ \text{RMSNorm}(x) = \frac{x}{\sqrt{\frac{1}{n}\sum_{i=1}^{n} x_i^2 + \epsilon}} \cdot \gamma RMSNorm(x)=n1∑i=1nxi2+ϵ x⋅γ

python 复制代码

import torch
import torch.nn as nn
class RMSNorm(nn.Module):
    # dim：归一化的维度大小
    # eps：防止除零的非常小的数值
    def __init__(self, dim: int, eps: float = 1e-6):
        super().__init__()
        self.eps = eps
        # 初始化可学习参数weight，初始值为全1，形状(dim,)
        self.weight = nn.Parameter(torch.ones(dim))

    # 定义内部方法_nrom, 用于对输入x进行归一化
    def _norm(self, x):
        # x.pow(2).mean(-1, keepdim=True) x平方后，对最后一个维度求均值，并保持维度不变
        # x: [batch_size, seq_len, dim] -> [batch_size, seq_len, 1]
        # torch.rsqrt(x) = 1/sqrt(x)
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)
    # 定义前向传播操作   
    def forward(self, x):
        # x: [batch_size, seq_len, dim] 为保证精度，先转化为浮点数进行计算，最后再转化为原类型
        norm = self._norm(x.float()).type_as(x)
        return self.weight * norm

batch_sizes =3
seq_len = 4
dim = 5
exp = torch.rand(batch_sizes, seq_len, dim)
rms_norm_layer = RMSNorm(dim=dim)
exp_rmsNorm = rms_norm_layer.forward(exp)
print(exp_rmsNorm)

3.3 旋转位置编码(RoPE)

在LLaMA(Large Language Model Meta AI)中，使用旋转位置编码(Rotary Positional Embedding)引入位置信息。顾名思义，旋转位置编码就是通过旋转矩阵将位置信息嵌入到序列中。
旋转位置编码(RoPE)的核心思想是将位置编码嵌入到每个输入的特征维度中，不像传统的绝对位置编码那样为每个位置生成单独的向量。具体而言，RoPE将输入特征通过一个与位置相关的旋转特征，在不同位置上通过旋转不同角度来表达位置信息。

3.4 旋转位置编码的具体流程

旋转位置编码的具体流程如下：

x 1 x_1 x1和 x 2 x_2 x2是token的原始编码值。
θ1 (theta1) 是一个常数，为每两维度的编码设置，将 [ θ 1 , θ 2 ... θ d / 2 ] [θ₁,θ₂...θ_{d/2}] [θ1,θ2...θd/2]这个序列总称为"频率"。
m 是 position（位置），表示当前 token 在序列中的位置。
通过 m * θ 计算角度，并将 x 1 x_1 x1和 x 2 x_2 x2按照这个角度进行旋转，得到新的编码 x 1 ′ x^{'}{1} x1′ 和 x 2 ′ x^{'}{2} x2′。

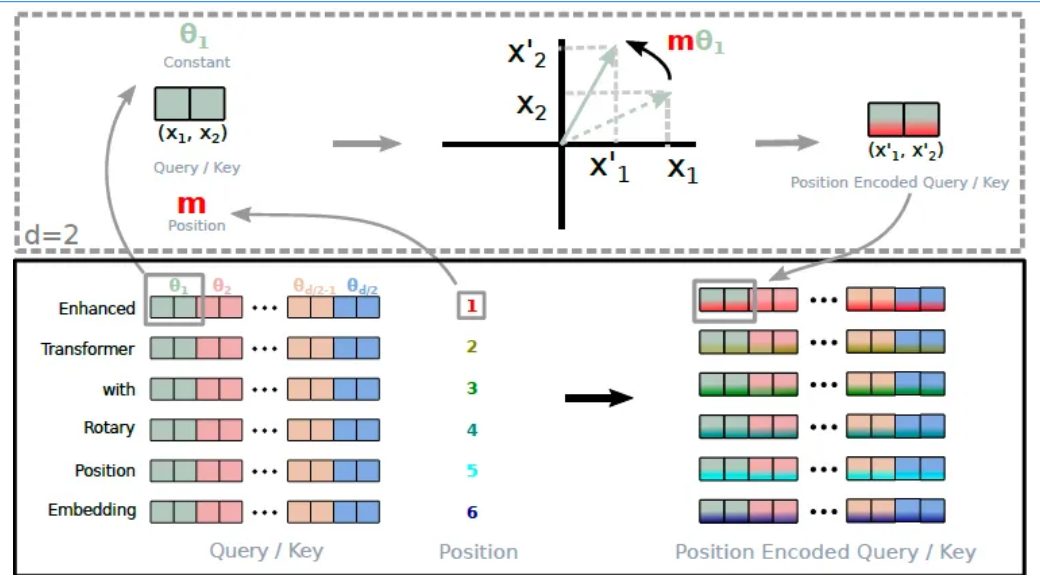
核心原理： 这个过程的核心是通过旋转操作引入位置相关的信息，这种方法可以使得模型对相对位置更加敏感，同时保持旋转不变性。

3.5 RoPE（旋转位置编码）核心内容

嵌入位置信息：通过使用旋转矩阵，RoPE能够在同一特征空间中嵌入位置信息，并且这种旋转变换可以是连续的，使得模型可以处理不同长度的序列输入，而不依赖于绝对位置编码的长度限制。
特征维度的分组旋转：RoPE会将输入特征维度两两分组，并将每对特征维度进行角度旋转，旋转角度根据序列中的相对位置来调整。随着序列位置的变化，每个特征都会以不同的旋转角度进行变化，从而实现位置的编码。
优点
- 相对位置感知：RoPE自然具备相对位置感知能力（因为它具有一定的循环性），因此模型可以更好地处理较长序列中的相对位置信息。
- 长度灵活性：相比于绝对位置编码，RoPE可以更加灵活地处理不同长度的序列，而不会受到编码长度的限制。
- 平滑的位置信息传递：通过旋转变换的方式嵌入位置信息，使得位置信息在整个特征空间中平滑地传递，避免了绝对位置编码的离散性。

3.6 旋转位置编码的理解

简单来说，RoPE的核心思想就是利用极坐标中的旋转来表示序列中的位置信息。
旋转位置编码本质上是一种在高维空间中进行的、基于极坐标思想的几何变换。它将词的语义信息（向量的模和初始方向）与位置信息（旋转的角度）优雅地解耦并融合在一起。通过在不同频率的二维平面上进行不同速度的旋转，RoPE为模型提供了一种既能捕捉相对位置、又具备良好外推能力的强大位置表示方法。

3.6.1 从笛卡尔坐标到极坐标：理解旋转的本质

首先，我们回顾一下二维平面中的点。一个点可以用两种方式表示：

笛卡尔坐标 ：(x, y)
极坐标 ：(r, θ)，其中 r 是点到原点的距离，θ 是点与x轴正方向的夹角。
一个从 (x, y) 到 (x', y') 的旋转，可以看作是保持其极径 r 不变，只改变其极角 θ 的过程。

根据三角函数，这个旋转可以用一个旋转矩阵来表示：

bash 复制代码

[x'] = [cos(Δθ)  -sin(Δθ)] [x]
[y']   [sin(Δθ)   cos(Δθ)] [y]

其中 Δθ 是旋转的角度。这就是RoPE中"旋转"一词的数学来源。

3.6.2 RoPE如何应用旋转：从二维到高维

RoPE的巧妙之处在于，它将这个二维的旋转思想扩展到了高维空间。

分组处理 ：假设一个词向量的维度是 d（例如4096），RoPE并不会一次性旋转整个向量。而是将维度两两分组，形成 d/2 个二维平面。例如，维度 (0, 1) 组成一个二维平面，(2, 3) 组成另一个，以此类推。
为每个平面分配不同的"频率" ：RoPE为每一个二维平面分配一个固定的旋转"基准频率"，我们称之为 θ_i（其中 i 是平面的索引）。这个频率是预先计算好的，通常使用一个公式（如 θ_i = 10000^(-2i/d)）来生成，使得不同平面的频率呈指数级变化。
根据位置 m 计算旋转角度 ：对于一个在序列中位置为 m 的词，它在第 i 个二维平面上的旋转角度 Δθ 被定义为 m * θ_i。
- 这意味着：位置 m 越大 ，旋转的角度就越大。不同的平面 i ，因为基准频率 θ_i 不同，所以旋转的速度也不同。低频平面（i 小）旋转得慢，高频平面（i 大）旋转得快。

3.6.3 极坐标视角下的RoPE公式

假设有一个词向量，取其中的一对 (x₁, x₂)，它们对应第 i 个二维平面。

原始状态 (m=0) ：
- 在位置 m=0 时，旋转角度 m * θ_i = 0。所以向量不旋转，保持原样 (x₁, x₂)。我们可以把它看作是极坐标 (r, θ₀)，其中 r = sqrt(x₁² + x₂²)，θ₀ 是它的初始角度。
移动到位置 m ：
- 现在，这个词移动到了位置 m。RoPE要求我们将 (x₁, x₂) 这个向量旋转 m * θ_i 的角度。从极坐标角度看，这相当于保持极径 r 不变，将极角从 θ₀ 变为 θ₀ + m * θ_i。
计算新坐标 (x'₁, x'₂) ：RoPE的公式（使用旋转矩阵）是：
bash x'₁ = x₁ * cos(m * θ_i) - x₂ * sin(m * θ_i) x'₂ = x₁ * sin(m * θ_i) + x₂ * cos(m * θ_i)
- 这正是将笛卡尔坐标 (x₁, x₂) 旋转 m * θ_i 角度后得到的新笛卡尔坐标 (x'₁, x'₂)。

3.7 RoPE代码实现(Pytorch风格)

python 复制代码

import torch
import torch.nn as nn

def precompute_pos_cis(dim: int, max_position: int, theta: float = 10000.0):
    """
    预计算所有位置的旋转位置编码。

    该函数利用欧拉公式 e^(i*x) = cos(x) + i*sin(x) 来高效地生成旋转矩阵。
    它将旋转操作表示为复平面上的单位向量，其角度由位置和频率决定。

    Args:
        dim (int): 词嵌入的维度。例如，对于4096维的嵌入，dim=4096。
                   注意：这个维度必须是偶数，因为它是成对处理的。
        max_position (int): 模型能够处理的最大序列长度。例如，2048或4096。
        theta (float): 一个超参数，用于控制频率的缩放。通常设置为10000.0。
                       这个值越大，低频部分的频率就越低，使得位置变化对低维特征的影响更平滑。
    Returns:
        torch.Tensor: 一个形状为 (max_position, dim // 2) 的复数张量。
                      每一行代表一个位置 `m` 的旋转编码。
                      每一行是一个复数向量，其中每个复数代表一个二维平面上的旋转。
    """

    # 步骤 1: 计算每个维度对的基准频率 (θ_i)
    # ---------------------------------------------------------
    # RoPE 的核心思想是为每一对维度 (x1, x2) 分配一个不同的旋转频率。
    # 这个频率序列 [θ_0, θ_1, ..., θ_{dim/2 - 1}] 是根据公式计算的：
    # θ_i = 1 / (10000^(2i / dim))
    # 这里的代码通过 torch.arange(0, dim, 2) 来获取索引 [0, 2, 4, ...]，然后除以 dim 来实现 2i/dim 的效果。
    # `[: (dim // 2)]` 确保我们只取 dim/2 个频率值。
    # `float()` 将整数张量转换为浮点数张量以便进行指数运算。 特征维度越大，频率越小
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    # `freqs` 的形状是 (dim // 2,)，它包含了所有维度对的基准频率。

    # 步骤 2: 生成所有位置索引 (m)
    # ---------------------------------------------------------
    # 创建一个从 0 到 max_position - 1 的整数张量，代表序列中的每一个位置。
    # `device=freqs.device` 确保位置张量和频率张量在同一个计算设备上（CPU或GPU）。
    m = torch.arange(max_position, device=freqs.device)
    # `m` 的形状是 (max_position,)

    # 步骤 3: 计算每个位置在每个频率下的旋转角度 (m * θ_i)
    # ---------------------------------------------------------
    # 使用 `torch.outer` 计算 `m` 和 `freqs` 的外积。
    # 这会生成一个矩阵，其中元素 [i, j] 的值是 m[i] * freqs[j]。
    # 这个矩阵的每一行 `i` 代表了位置 `m[i]` 在所有 `dim/2` 个维度对上的旋转角度。
    # `freqs` 的形状 (max_position, dim // 2)
    freqs = torch.outer(m, freqs).float()

    # 步骤 4: 使用极坐标形式创建复数旋转向量
    # ---------------------------------------------------------
    # 这是 RoPE 实现中最巧妙的一步。
    # 我们不直接计算 cos(m*θ_i) 和 sin(m*θ_i)，而是使用 `torch.polar` 来创建复数。
    # `torch.polar(abs, angle)` 会创建一个复数，其模长为 `abs`，辐角（角度）为 `angle`。
    # `torch.ones_like(freqs)`：将所有复数的模长设置为 1。因为旋转变换不改变向量的长度。
    # `freqs`：将上一步计算出的角度矩阵作为复数的辐角。
    # 根据欧拉公式，`polar(1, angle)` 等价于 `cos(angle) + i * sin(angle)`。
    # 这个复数完美地代表了在二维平面上的一个旋转操作。
    pos_cis = torch.polar(torch.ones_like(freqs), freqs)
    # `pos_cis` 的形状是 (max_position, dim // 2)，是一个复数张量。

    return pos_cis

特征维度越大，频率越小

python 复制代码

# 频率与维度的关系图
import numpy as np
import matplotlib.pyplot as plt

# Parameters
theta = 10000.0
dim = 128  # Example dimension size

# Calculate freqs as per the formula
freqs = 1.0 / (theta ** (np.arange(0, dim, 2)[: (dim // 2)] / dim))

# Plotting the freqs
plt.figure(figsize=(8, 6))
plt.plot(freqs, marker='o', linestyle='-', color='b', label='Freqs vs Dimension')
plt.title("Change in freqs with increasing dimension")
plt.xlabel("Dimension")
plt.ylabel("Freqs") 
plt.grid(True)
plt.legend()
plt.show()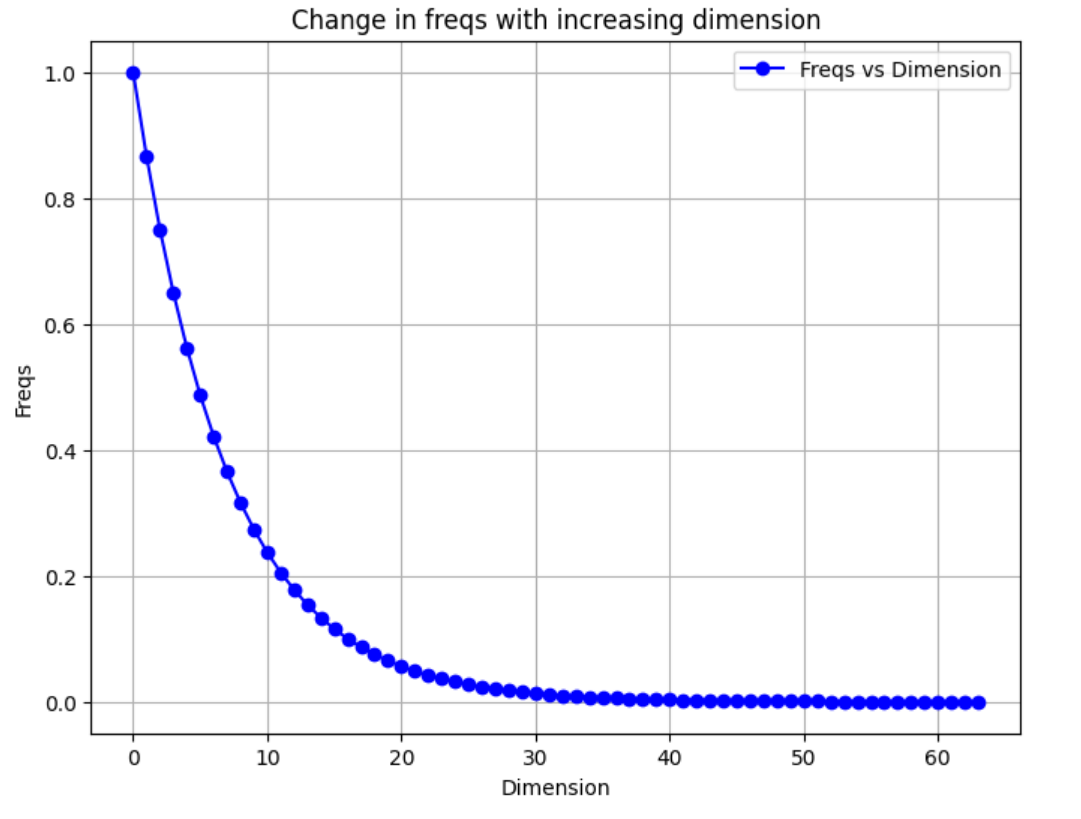

完整代码

python 复制代码

import torch
import torch.nn as nn

def precompute_pos_cis(dim: int, max_position: int, theta: float = 10000.0):
    """
    预计算所有位置的旋转位置编码。

    该函数利用欧拉公式 e^(i*x) = cos(x) + i*sin(x) 来高效地生成旋转矩阵。
    它将旋转操作表示为复平面上的单位向量，其角度由位置和频率决定。

    Args:
        dim (int): 词嵌入的维度。例如，对于4096维的嵌入，dim=4096。
                   注意：这个维度必须是偶数，因为它是成对处理的。
        max_position (int): 模型能够处理的最大序列长度。例如，2048或4096。
        theta (float): 一个超参数，用于控制频率的缩放。通常设置为10000.0。

    Returns:
        torch.Tensor: 一个形状为 (max_position, dim // 2) 的复数张量。
                      每一行代表一个位置 `m` 的旋转编码。
    """
    # 步骤 1: 计算每个维度对的基准频率 (θ_i)
    # 公式: θ_i = 1 / (10000^(2i / dim))
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))

    # 步骤 2: 生成所有位置索引 (m)
    m = torch.arange(max_position, device=freqs.device)

    # 步骤 3: 计算每个位置在每个频率下的旋转角度 (m * θ_i)
    freqs = torch.outer(m, freqs).float()

    # 步骤 4: 使用极坐标形式创建复数旋转向量
    # polar(abs, angle) 等价于 abs * (cos(angle) + i * sin(angle))
    # 这里 abs=1, 所以就是 cos(angle) + i * sin(angle)，即单位圆上的旋转
    pos_cis = torch.polar(torch.ones_like(freqs), freqs)

    return pos_cis

# 将频率用于q k矩阵
def apply_rotary_emb(xq, xk, pos_cis):
    """
    应用旋转位置编码到查询矩阵和键矩阵
    
    Args:
        xq: 查询矩阵，形状为 [batch_size, seq_len, num_heads, head_dim]
        xk: 键矩阵，形状为 [batch_size, seq_len, num_heads, head_dim]
        pos_cis: 预计算的旋转位置编码，形状为 [max_seq_len, head_dim//2] 的复数张量
    
    Returns:
        xq_out: 应用旋转位置编码后的查询矩阵
        xk_out: 应用旋转位置编码后的键矩阵
    """
    
    def unite_shape(pos_cis, x):
        """
        调整pos_cis的形状以匹配输入张量x的广播要求
        
        Args:
            pos_cis: 旋转位置编码，形状为 [seq_len, head_dim//2]
            x: 目标张量，形状为 [batch_size, seq_len, num_heads, head_dim//2]
        
        Returns:
            调整形状后的pos_cis，可以与x进行广播运算
        """
        ndim = x.ndim  # 获取x的维度数，通常为4
        assert 0 <= 1 < ndim  # 确保第1维（序列长度维度）存在
        assert pos_cis.shape == (x.shape[1], x.shape[-1])  # 确保pos_cis形状匹配
        
        # 创建新的形状：只在序列长度维度和最后一维保持原始大小，其他维度设为1
        # 这样可以通过广播机制应用到所有批次和注意力头
        shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
        return pos_cis.view(*shape)

    # 步骤1: 将实数张量转换为复数张量
    # 将xq的最后一维从head_dim重塑为(head_dim//2, 2)，然后转换为复数
    # 例如：[batch, seq_len, num_heads, head_dim] -> [batch, seq_len, num_heads, head_dim//2]
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    
    # 步骤2: 调整pos_cis的形状以匹配xq_的广播要求
    # pos_cis形状从 [seq_len, head_dim//2] 调整为 [1, seq_len, 1, head_dim//2]
    pos_cis = unite_shape(pos_cis, xq_)
    
    # 步骤3: 应用旋转位置编码
    # 通过复数乘法实现旋转：xq_out = xq_ * pos_cis
    # 这相当于对每个二维平面进行旋转变换
    xq_out = torch.view_as_real(xq_ * pos_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * pos_cis).flatten(3)
    
    # 步骤4: 恢复原始数据类型并返回
    # flatten(3)将复数的实部和虚部重新展平，恢复为原始的head_dim维度
    return xq_out.type_as(xq), xk_out.type_as(xk)

# 使用示例
if __name__ == "__main__":
    # 模拟参数
    batch_size = 2
    seq_len = 512
    num_heads = 8
    head_dim = 64  # 必须是偶数
    
    # 创建模拟的查询和键矩阵
    xq = torch.randn(batch_size, seq_len, num_heads, head_dim)
    xk = torch.randn(batch_size, seq_len, num_heads, head_dim)
    
    # 【修改部分】使用precompute_pos_cis函数正确生成旋转位置编码
    # 注意：这里的dim应该是head_dim，而不是整个模型的维度
    # max_position应该大于或等于实际序列长度seq_len
    pos_cis = precompute_pos_cis(dim=head_dim, max_position=seq_len)
    
    # 从预计算的pos_cis中截取当前序列长度所需的部分
    # pos_cis的形状是 [seq_len, head_dim//2]
    current_pos_cis = pos_cis[:seq_len]
    
    # 应用旋转位置编码
    xq_rotated, xk_rotated = apply_rotary_emb(xq, xk, current_pos_cis)
    
    print(f"原始查询矩阵形状: {xq.shape}")
    print(f"旋转后查询矩阵形状: {xq_rotated.shape}")
    print(f"原始键矩阵形状: {xk.shape}")
    print(f"旋转后键矩阵形状: {xk_rotated.shape}")
    
    # 验证旋转是否改变了向量的模长（旋转不应该改变模长）
    original_norm = torch.norm(xq, dim=-1)
    rotated_norm = torch.norm(xq_rotated, dim=-1)
    print(f"原始向量模长: {original_norm[0, 0, 0]:.4f}")
    print(f"旋转后向量模长: {rotated_norm[0, 0, 0]:.4f}")
    print(f"模长差异: {torch.abs(original_norm - rotated_norm).max():.10f}")

bash 复制代码

原始查询矩阵形状: torch.Size([2, 512, 8, 64])
旋转后查询矩阵形状: torch.Size([2, 512, 8, 64])
原始键矩阵形状: torch.Size([2, 512, 8, 64])
旋转后键矩阵形状: torch.Size([2, 512, 8, 64])
原始向量模长: 8.7612
旋转后向量模长: 8.7612
模长差异: 0.0000014305

3.8 旋转位置编码仅应用Q和K矩阵的理解

旋转位置编码仅应用Q(Query)和K(Key)矩阵，而不应用于V(Value)矩阵。这与自注意力机制的工作原理以及相对位置信息的处理方式有关。

3.8.1 Q、K矩阵与相对位置编码的关联

在自注意力机制中，注意力权重通过计算Query和Key的点积来获得，具体公式为
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Q ：查询矩阵， K ：键矩阵， V ：值矩阵 Attention(Q,K,V)= softmax(\frac{QK^T}{ \sqrt{d_k} })V \\ Q：查询矩阵，K：键矩阵，V：值矩阵 Attention(Q,K,V)=softmax(dk QKT)VQ：查询矩阵，K：键矩阵，V：值矩阵

通过计算，Query和Key的点积决定了每个位置之间的相对相关性。如果希望通过位置编码让模型意识到输入序列中元素的相对位置，那么只需要将旋转位置应用于Q和K，因为它们参与了点击计算，并直接影响注意力得分。
RoPE为QK计算引入相对位置感知：RoPE的旋转操作对Q和K矩阵的特征进行旋转变换，这会改变它们的内积结果，从而为模型注入了相对位置信息。这样，RoPE能够在QK点积时，隐含地捕捉到输入序列中元素之间的相对位置关系。

3.8.2 RoPE不应用于V矩阵的解释

V矩阵知识根据计算出的注意力权重进行加权，没有必要引入位置信息。如果对V矩阵应用ROPE，反而会破坏其携带的原始特征信息。
注意力机制的重点在于位置之间的相对关系，RoPE正是通过对Q和K矩阵进行旋转，将相对位置信息引入点积结果中。由于V矩阵不参与计算相似性，使用RoPE对其进行变换没有实际意义。
注意力机制的计算量主要集中在QK点积和注意力权重的计算上。如果对V矩阵也应用RoPE，只会增加额外的计算复杂度和参数量，且不会特升模型性能。因此，RoPE只应用于Q和K，有助于保持计算效率。

3.8.3 位置编码的内推和外推

内推定义：当测试序列长度≤训练时最大序列长度（如128个token）时，模型使用已见过的位置编码进行推理。
外推定义：当测试序列长度＞训练时最大序列长度时，模型需要推断未见过的长序列位置编码。
训练策略：
- 外推评估：使用比训练集更长的测试序列评估模型表现。
- 能力提升：通过外推测试迫使模型增强长序列处理能力，类似"让学习者解答未学过的题目"。

四 LLama中的注意力机制与KV缓存

KV缓存（Key-Value Cache）是Transformer模型在执行自回归生成任务（如文本生成）时的一项关键加速技术，尤其在处理长序列时效果显著。该机制通过避免重复计算，大幅提升了推理效率。
KV缓存主要应用于解码器架构，是GPT系列等自回归模型的核心优化之一。在自回归生成过程中，模型会逐个生成序列中的token。以文本生成为例，每一步模型都会基于已生成的全部历史tokens，来预测下一个新token。
如果没有KV缓存，模型在每一步都需要重新计算所有历史token与新token之间的自注意力（self-attention），这包含了大量冗余计算。而KV缓存机制正是为了解决这一问题。
在Transformer的每一层中，注意力机制会基于输入生成查询（Query）、键（Key）和值(Value）。计算公式如下：
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)= softmax(\frac{QK^T}{ \sqrt{d_k} })V \\ Attention(Q,K,V)=softmax(dk QKT)V
Query：代表当前的token信息，它用于寻找与其他tokens相关的内容。
Key和Value分别代表历史tokens的信息，它们在每个生成步骤中被重新计算。这会导致计算量成倍增加。如果，生成100个token，每一步都会重新计算前面99个token和当前token的注意力，这种操作十分耗时。
KV缓存的核心思想是避免重复计算注意力层(self-attention)中的键（Key）和值（Value）。KV缓存通过将生成过程中每个token的Key和Value保存在缓存中，只在第一次生成时计算一次Key和Value，在生成后续token时，模型只需重新计算新token的Query，直接使用缓存中的Key和Value，避免对历史tokens的重复计算。

KV缓存的优点

提高生成速度：由于避免对已生成token的重复计算，KV缓存机制可显著减少生产时间。
节省计算资源：缓存Key和Value后，每一步仅需计算当前token和Query，而Key和Value从缓存获取，大幅减少计算量。
降低复杂度：使用缓存后，生成过程中注意力机制的复杂度从 O ( n 2 ) O(n^2) O(n2)降低到 O ( n ) O(n) O(n)， n n n为序列长度，对于长序列生成任务，加速效果显著。

4.1 KV缓存机制的工作原理

KV缓存机制的详细工作原理：

初始化：
- 当生成开始时，模型计算输入序列的Key和Value，并将这些计算结果缓存起来，保存在内存中。每个注意力层都会有一对Key-Value缓存。
- 这些缓存的Key和Value会存储到KV缓存中，并作为后续生成步骤中的参考。
生成过程中：
- 当生成下一个token时，模型不需要重新计算前面已经生成的token的Key和Value。它会直接使用之前缓存的key和Value。
- 只需要计算当前token的Query，并将它与已经缓存的Key进行点积计算，得出注意力分数。
- 这些注意力分数会结合缓存的Value来计算当前token的输出。
更新缓存：
- 对于每一个生成步骤，模型还会将当前生成的token的Key和Value加入缓存，确保缓存中的Key和Value始终保持更新，包含所有已经生成的tokens。
- 缓存的大小会逐渐增加，最终会包含所有生成序列的Key和Value。
加速效果：
- 由于每个生成步骤只需要计算当前token的Query，而不需要重新计算整个序列的Key和Value，这大大减少计算量。
- 随着序列长度增加，缓存的使用能够显著减少时间复杂度，使生成过程更快。

更加详细的过程参看LLama 3分组查询注意力与KV缓存机制

4.2 KV重复匹配Q代码案例实现

这通常用于Transformer模型中，当key/value头的数量需要与query头数量匹配时使用。

python 复制代码

'''
接收一个4维张量 x 和重复次数 n_rep
如果 n_rep 为1，直接返回原张量
否则，通过添加新维度、扩展和重塑操作，在第3维（key/value头维度）上进行重复
最终将 n_kv_heads 扩展为 n_kv_heads * n_rep
'''
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """torch.repeat_interleave(x, dim=2, repeats=n_rep)"""
    bs, slen, n_kv_heads, head_dim = x.shape
    if n_rep == 1:
        return x
    return (
        x[:, :, :, None, :]
        .expand(bs, slen, n_kv_heads, n_rep, head_dim)
        .reshape(bs, slen, n_kv_heads * n_rep, head_dim)
    )

python 复制代码

import torch  # 导入PyTorch库，用于张量操作

def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """
    重复 Key/Value 头以匹配 Query 头的数量。
    
    这个函数主要用于多组查询注意力（Multi-Query Attention 或 Grouped-Query Attention）。
    在这种架构下，Key和Value的"头"数量（n_kv_heads）通常少于Query的"头"数量（n_heads）。
    为了让每个Query头都能与对应的Key/Value头进行计算，我们需要将Key/Value张量复制若干次。
    
    Args:
        x (torch.Tensor): 输入的张量，形状为 [batch_size, sequence_length, n_kv_heads, head_dim]。
                          - batch_size: 一批处理多少个序列
                          - sequence_length: 序列的长度（例如，一个句子有多少个token）
                          - n_kv_heads: Key/Value头的数量
                          - head_dim: 每个头内部的维度（向量长度）
        n_rep (int): 重复的次数。通常 n_rep = n_heads / n_kv_heads。
    
    Returns:
        torch.Tensor: 重复后的张量，形状变为 [batch_size, sequence_length, n_kv_heads * n_rep, head_dim]。
                      这个新形状确保了Key/Value头的总数与Query头数量匹配。
    """
    # 1. 解构输入张量的形状，获取每个维度的大小，方便后续使用。
    bs, slen, n_kv_heads, head_dim = x.shape
    #    bs      -> batch size (批大小)
    #    slen    -> sequence length (序列长度)
    #    n_kv_heads -> number of key/value heads (K/V头数量)
    #    head_dim -> dimension of each head (每个头的维度)

    # 2. 优化：如果重复次数为1，说明K/V头和Q头数量已经匹配，无需任何操作，直接返回原张量。
    if n_rep == 1:
        return x

    # 3. 核心操作：通过三步实现高效的维度复制。
    #    目标：将第3维 (n_kv_heads) 的每个元素，沿着该维度复制 n_rep 次。
    
    # 步骤 A: 增加一个新维度
    # 原始形状: [bs, slen, n_kv_heads, head_dim]
    # x[:, :, :, None, :] 会在第3维和第4维之间插入一个大小为1的新维度。
    # [:, :, :, None, :] 的含义是：保留所有维度，但在第3维（索引为3）的位置增加一个维度。
    # 新形状: [bs, slen, n_kv_heads, 1, head_dim]
    # 这个新维度是我们用来"填充"副本的地方。
    expanded_x = x[:, :, :, None, :]

    # 步骤 B: 扩展新维度
    # .expand() 方法会将大小为1的维度"拉伸"到指定的大小，这不会实际复制数据，只是创建了一个新的"视图"，非常高效。
    # 我们将新创建的第4维从1扩展到 n_rep。
    # 扩展后形状: [bs, slen, n_kv_heads, n_rep, head_dim]
    # 此时，可以想象成，原来的每个K/V头都变成了 n_rep 个"并排"的头。
    tiled_x = expanded_x.expand(bs, slen, n_kv_heads, n_rep, head_dim)

    # 步骤 C: 重塑张量
    # .reshape() 会改变张量的视图，将维度合并。
    # 我们将第3维 (n_kv_heads) 和第4维 (n_rep) 合并成一个维度。
    # 合并后的大小为 n_kv_heads * n_rep。
    # 最终形状: [bs, slen, n_kv_heads * n_rep, head_dim]
    # 这样，我们就成功地将K/V头的数量扩展到了与Q头匹配的数量。
    final_x = tiled_x.reshape(bs, slen, n_kv_heads * n_rep, head_dim)
    
    return final_x

# --- 举个例子来帮助理解 ---

# 假设我们有一个批大小为2，序列长度为5的输入
# 原始模型有 2 个 K/V 头，但 6 个 Q 头
# 所以我们需要将 K/V 头重复 6 / 2 = 3 次
batch_size = 2
seq_len = 5
n_kv_heads = 2
n_q_heads = 6
head_dim = 8  # 每个头是8维向量

# 创建一个模拟的 K/V 张量
kv_tensor = torch.randn(batch_size, seq_len, n_kv_heads, head_dim)
print(f"原始 K/V 张量形状: {kv_tensor.shape}") # 应该输出: torch.Size([2, 5, 2, 8])

# 计算需要重复的次数
n_rep = n_q_heads // n_kv_heads # 6 // 2 = 3

# 调用函数
repeated_kv_tensor = repeat_kv(kv_tensor, n_rep)

print(f"重复后的 K/V 张量形状: {repeated_kv_tensor.shape}") # 应该输出: torch.Size([2, 5, 6, 8])

# 验证一下：第0个K/V头的内容是否被复制了3次？
# 原始的第0个头
original_head_0 = kv_tensor[0, 0, 0, :]
# 重复后的第0, 1, 2个头
repeated_head_0 = repeated_kv_tensor[0, 0, 0, :]
repeated_head_1 = repeated_kv_tensor[0, 0, 1, :]
repeated_head_2 = repeated_kv_tensor[0, 0, 2, :]

# 使用 torch.allclose 检查内容相同
print(f"第0个头被正确复制到第0个新头: {torch.allclose(original_head_0, repeated_head_0)}") # True
print(f"第0个头被正确复制到第1个新头: {torch.allclose(original_head_0, repeated_head_1)}") # True
print(f"第0个头被正确复制到第2个新头: {torch.allclose(original_head_0, repeated_head_2)}") # True

KV缓存有助于提高生成速度、节约计算资源，降低注意力机制的复杂度。

4.3 LLama注意力机制的实现代码

LMConfig配置文件

python 复制代码

from transformers import PretrainedConfig
from typing import List


class LMConfig(PretrainedConfig):
    model_type = "MateConv_LlaMA"

    def __init__(
            self,
            dim: int = 512,
            n_layers: int = 8,
            n_heads: int = 16,
            n_kv_heads: int = 8,
            vocab_size: int = 6400,
            hidden_dim: int = None,
            multiple_of: int = 64,
            norm_eps: float = 1e-5,
            max_seq_len: int = 512,
            dropout: float = 0.0,
            flash_attn: bool = True,
            use_moe: bool = False,
            num_experts_per_tok=2,
            n_routed_experts=4,
            n_shared_experts: bool = True,
            scoring_func='softmax',
            aux_loss_alpha=0.01,
            seq_aux=True,
            norm_topk_prob=True,
            **kwargs,
    ):
        self.dim = dim
        self.n_layers = n_layers
        self.n_heads = n_heads
        self.n_kv_heads = n_kv_heads
        self.vocab_size = vocab_size
        self.hidden_dim = hidden_dim
        self.multiple_of = multiple_of
        self.norm_eps = norm_eps
        self.max_seq_len = max_seq_len
        self.dropout = dropout
        self.flash_attn = flash_attn
        self.use_moe = use_moe
        self.num_experts_per_tok = num_experts_per_tok  # 每个token选择的专家数量
        self.n_routed_experts = n_routed_experts  # 总的专家数量
        self.n_shared_experts = n_shared_experts  # 共享专家
        self.scoring_func = scoring_func  # 评分函数，默认为softmax
        self.aux_loss_alpha = aux_loss_alpha  # 辅助损失的alpha参数
        self.seq_aux = seq_aux  # 是否在序列级别上计算辅助损失
        self.norm_topk_prob = norm_topk_prob  # 是否标准化top-k概率
        super().__init__(**kwargs)

LLama注意力层代码案例（大佬，请狠狠研究，菜鸟请暂时放弃）

python 复制代码

class Attention(nn.Module):
    def __init__(self, args: LMConfig):
        super().__init__()

        # 先确定n_kv_heads的值，如果设置了单独的n_kv_heads，就执行多头共享机制
        # 如果没设置kv_heads，就意味着全部的头都要执行kv缓存，此时n_kv_heads = n_heads
        self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads

        # 检验，n_heads能否被n_kv_heads除尽
        assert args.n_heads % self.n_kv_heads == 0

        # 设置头数、kv缓存头数和重复次数
        self.n_local_heads = args.n_heads
        self.n_local_kv_heads = self.n_kv_heads
        self.n_rep = self.n_local_heads // self.n_local_kv_heads

        # 设置每个头上的特征维度
        self.head_dim = args.dim // args.n_heads

        # 设置权重层，当 x 的结构为 (seq_len, d_model)时
        # 常规的Q、K、V矩阵的结构应该与 X 一致，也是 (seq_len, d_model)
        # 因此常规的 w 应该是 (d_model,d_model)结构
        # 在多头注意力中，w 应该是 (d_model, d_model/n_heads)
        # 在具有kv缓存的情况下，我们是对所有头上的注意力并行计算
        # 因此Q的权重应该是(d_model, d_model)
        # K和V的权重应该是(d_model, d_model/n_heads * n_kv_heads)
        self.wq = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False)
        self.wk = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False)
        self.wv = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False)

        # 输出层上的O的权重不受影响，是(d_model, d_model)
        self.wo = nn.Linear(args.n_heads * self.head_dim, args.dim, bias=False)

        # 设置kv缓存初始值
        self.k_cache, self.v_cache = None, None

        # 设置注意力和残差连接上的dropout层和dropout比例
        self.attn_dropout = nn.Dropout(args.dropout)
        self.resid_dropout = nn.Dropout(args.dropout)
        self.dropout = args.dropout

        # flash attention
        # print("WARNING: using slow attention. Flash Attention requires PyTorch >= 2.0")
        self.flash = hasattr(torch.nn.functional, 'scaled_dot_product_attention') and args.flash_attn

        # 设置decoder专用前瞻掩码
        # 注意，前瞻掩码是用于QK.T矩阵的
        mask = torch.full((1, 1, args.max_seq_len, args.max_seq_len), float("-inf"))
        mask = torch.triu(mask, diagonal=1)

        # buffer用于保存神经网络中除了权重之外、需要被保存的静态数据们
        # 比如掩码矩阵、比如位置编码中的频率等等编码表
        # "mask"我们指定的buffer名称，我们可以通过self.mask来调出掩码矩阵
        self.register_buffer("mask", mask, persistent=False)

    # 设置旋转位置编码中的频率计算
    def _precompute_pos_cis(self, dim: int, max_position = 10000, theta: float = 10000.0):
        freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
        m = torch.arange(max_position, device=freqs.device)
        freqs = torch.outer(m, freqs).float()
        pos_cis = torch.polar(torch.ones_like(freqs), freqs)
        return pos_cis
    
    def forward(self, x: torch.Tensor, kv_cache=False):

        # 作为注意力机制，被输入的x就是原始数据x
        # 结构为 (bs, seq_len, d_model)
        bsz, seqlen, _ = x.shape

        # 无论是否执行KV缓存，Q的求解是不变的
        xq = self.wq(x)

        # 如果是训练模式下，K和V照常求解
        if self.train():
            # 将x输入线性层、转换为初始的K和V
            # 但是只需要n_kv_heads个头的部分
            xk, xv = self.wk(x), self.wv(x)

        # 如果是推理模式，且kv_cache设置是打开的
        # 那要判断现在是否是初次预测
        if kv_cache and self.eval():
            # kv缓存是否还是None？已经存在了吗？
            if all(cache is not None for cache in (self.k_cache, self.v_cache)):
                # 如果不是None，说明不是初次预测了，此时需要的是缓存更新
                xk_new_token = self.wk(x[:,-1,:]).unsqueeze(1)
                xv_new_token = self.wv(x[:,-1,:]).unsqueeze(1)
                xk = torch.cat((self.k_cache, xk_new_token), dim=1)
                xv = torch.cat((self.v_cache, xv_new_token), dim=1)
            else:
                # 如果k和v缓存中有一个为None，说明是初次预测
                xk, xv = self.wk(x), self.wv(x)
            #生成xk和xv后，把结果保存到缓存中
            self.k_cache, self.v_cache = xk, xv

        # 为了更省内存，我们要将数据结构重新整理后适应位置编码的结构
        # 可以将该流程命名为"多头旋转位置编码"
        xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
        xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
        xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)

        # 在Q和K上执行旋转位置编码
        pos_cis = self._precompute_pos_cis(self.head_dim, seqlen)
        xq, xk = apply_rotary_emb(xq, xk, pos_cis)

        # 将k矩阵和v矩阵进行重复
        xk = repeat_kv(xk, self.n_rep)  # (bs, seqlen, n_local_heads, head_dim)
        xv = repeat_kv(xv, self.n_rep)  # (bs, seqlen, n_local_heads, head_dim)

        # 矩阵乘法计算注意力分数时，要将n_heads作为第二维度
        # 因为实际要进行乘法的应该时 (seqlen, head_dim) 这样的二维表
        # transpose交换维度，结构变为(bs, n_local_heads, seqlen, head_dim)
        xq = xq.transpose(1, 2)
        xk = xk.transpose(1, 2)
        xv = xv.transpose(1, 2)

        # 如果使用flash attention的话
        # 就调用nn.functional下面的点乘注意力计算方法
        if self.flash and seqlen != 1:
            output = torch.nn.functional.scaled_dot_product_attention(xq, xk, xv
                                                                      , attn_mask=None #这里是padding掩码
                                                                      , dropout_p=self.dropout if self.training else 0.0
                                                                      , is_causal=True #这里是自动化的前瞻掩码
                                                                     )
        else:
            # 不使用flash attention，就自己计算
            # 这里的transpose是对最后两个维度的转置
            scores = torch.matmul(xq, xk.transpose(2, 3)) / math.sqrt(self.head_dim)
            
            # 在注意力分数上放上掩码
            # 如果有kv缓存的话，现在我们的kv矩阵可能会比掩码矩阵要大了
            # 获取缓存的长度
            cache_len = self.k_cache.shape[1] if self.k_cache is not None else 0
            total_len = cache_len + 1  # 当前总长度，等于历史缓存长度 + 当前序列长度

            # 检查是否需要扩展掩码矩阵
            if total_len > self.mask.shape[-1]:
                # 动态生成新的掩码，大小为 (seq_len + cache_len, seq_len + cache_len)
                new_mask = torch.full((1, 1, total_len, total_len), float("-inf")).to(x.device)
                new_mask = torch.triu(new_mask, diagonal=1)  # 生成前瞻掩码
                self.mask = new_mask  # 更新掩码矩阵
            
            scores = scores + self.mask[:, :, :seqlen, :seqlen]
                
            # 对最后一个维度求解softmax
            scores = F.softmax(scores.float(), dim=-1).type_as(xq)
            scores = self.attn_dropout(scores)
            output = torch.matmul(scores, xv)  # (bs, n_local_heads, seqlen, head_dim)

        # 最后再将结构转回来，并且将n_heads中的所有信息合并
        # contiguous() 用于确保张量在内存中的存储是连续的
        # 特别是在经过某些操作（如 transpose）后，这对后续的 view() 等操作至关重要，以避免错误
        output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)

        # 注意力机制的输出
        output = self.wo(output)
        output = self.resid_dropout(output)
        return output

模型验证

python 复制代码

import torch
import torch.nn as nn

# 假定的配置类
class LMConfig_:
    def __init__(self, n_heads=8, n_kv_heads=2, dim=512, max_seq_len=10000, dropout=0.1, flash_attn=False):
        self.n_heads = n_heads  # 注意力头的数量
        self.n_kv_heads = n_kv_heads  # KV共享头的数量
        self.dim = dim  # 模型的维度
        self.max_seq_len = max_seq_len  # 最大序列长度
        self.dropout = dropout  # dropout比例
        self.flash_attn = flash_attn  # 是否使用flash attention

# Attention类的测试实例化
args_ = LMConfig_()

# 重复kv
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """torch.repeat_interleave(x, dim=2, repeats=n_rep)"""
    bs, slen, n_kv_heads, head_dim = x.shape
    if n_rep == 1:
        return x
    return (
        x[:, :, :, None, :]
        .expand(bs, slen, n_kv_heads, n_rep, head_dim)
        .reshape(bs, slen, n_kv_heads * n_rep, head_dim)
    )

#将频率用于q、k矩阵
def apply_rotary_emb(xq, xk, pos_cis):
    def unite_shape(pos_cis, x):
        ndim = x.ndim
        assert 0 <= 1 < ndim
        assert pos_cis.shape == (x.shape[1], x.shape[-1])
        shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
        return pos_cis.view(*shape)

    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    pos_cis = unite_shape(pos_cis, xq_)
    xq_out = torch.view_as_real(xq_ * pos_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * pos_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

python 复制代码

# 创建假设输入
x = torch.randn(2, 10, 512)  # (batch_size=2, seq_len=10, dim=512)
pos_cis = precompute_pos_cis(dim=64, max_position = 10, theta=10000)

# 创建Attention实例
attention = Attention(args_)

# 前向传播
output = attention(x,kv_cache=True)
output.shape

五 LLama中的FFN with SwiGLU

5.1 FFN with SwiGLU

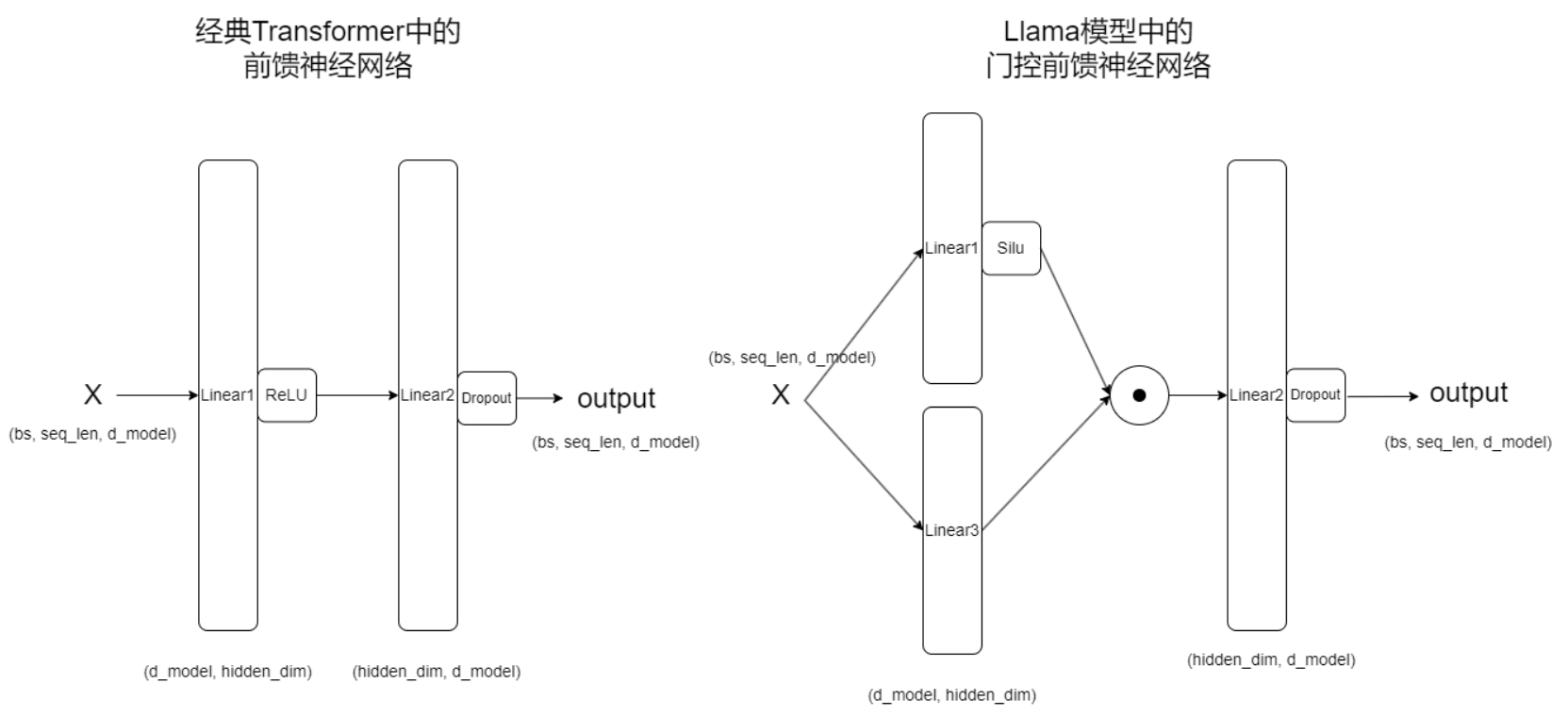
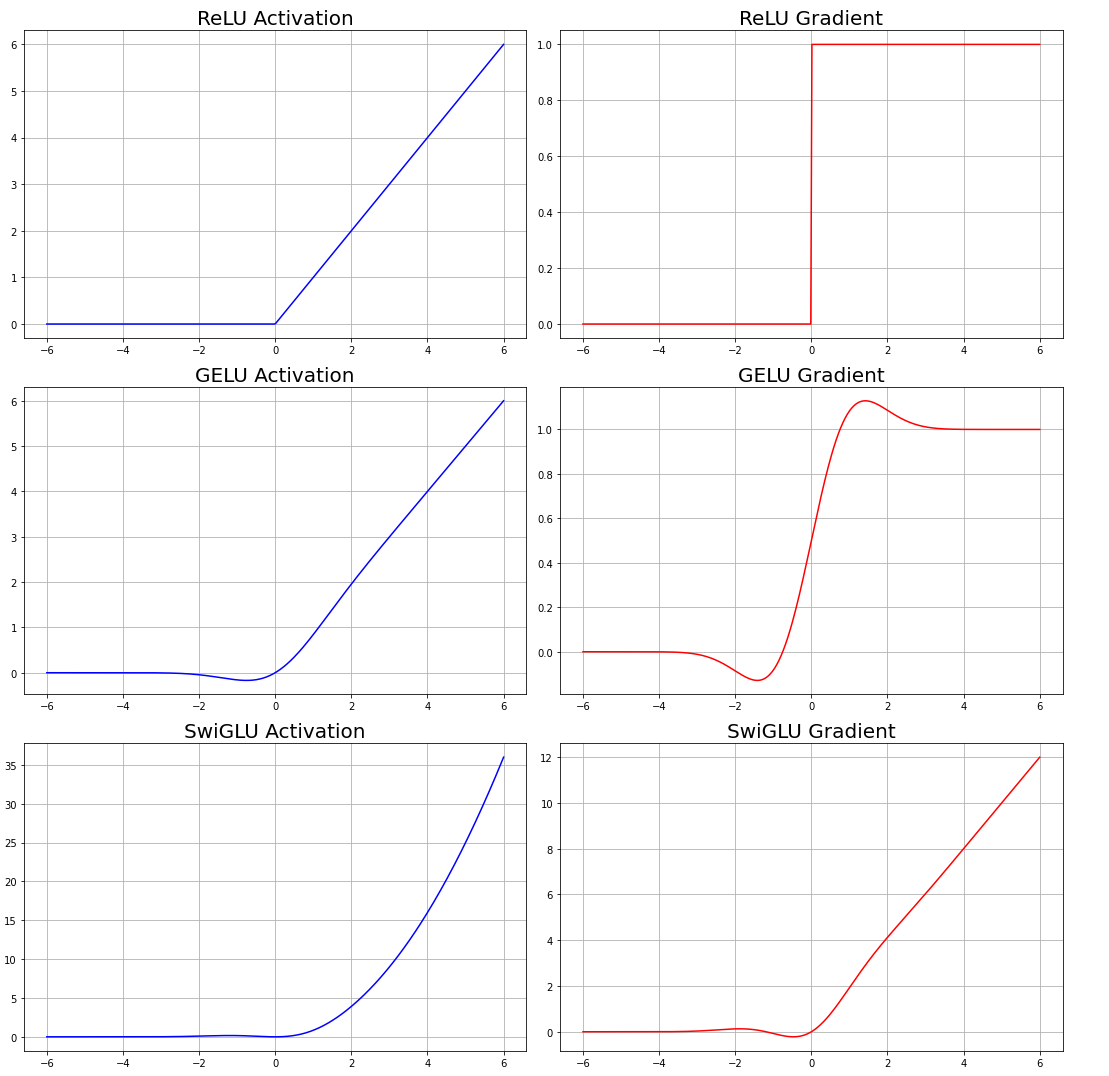
典型前馈网络 ： Output = Linear2 ( Activation ( Linear1 ( x ) ) ) \text{Output} = \text{Linear2}(\text{Activation}(\text{Linear1}(x))) Output=Linear2(Activation(Linear1(x)))

它通过一个线性层（Linear1），一个非线性激活函数（如ReLU或GELU），然后通过另一个线性层（Linear2）。

llama中的前馈神经网络
Output = Linear2 ( Activation ( Linear1 ( x ) ) ⊙ Linear3 ( x ) ) \text{Output} = \text{Linear2} \left( \textcolor{red}{\text{Activation}}\left( \textcolor{green}{\text{Linear1}}(x) \right) \odot \textcolor{gold}{\text{Linear3}}(x) \right) Output=Linear2(Activation(Linear1(x))⊙Linear3(x))

它通过两个线性层（Linear1和Linear3），从Linear1输出的结果经过silu激活函数后，与Linear3输出的结果进行逐元素乘法，然后通过另一个线性层（Linear2）。

SwiGLU（Switch-Gated Linear Unit）门控线性单元激活函数：SwiGLU 是一种新型的激活函数。SwiGLU 的设计核心是基于门控机制（gating mechanism），它通过引入两个线性路径的输出，并结合逐元素乘法，实现了对信息的动态控制。它被应用在 Transformer 的前馈网络（FFN）层中，用于增强网络的非线性表达能力和训练效率。

SwiGLU 激活函数：
SwiGLU ( x ) = GELU ( W 1 a ⋅ x ) ⊙ W 1 b ⋅ x \text{SwiGLU}(x) = \textcolor{red}{\text{GELU}}\left( \textcolor{green}{W_1^a} \cdot x \right) \odot \textcolor{gold}{W_1^b} \cdot x SwiGLU(x)=GELU(W1a⋅x)⊙W1b⋅x

W 1 a W_1^a W1a 和 W 1 b W_1^b W1b 是线性变换（全连接层）。
⊙ \odot ⊙ 表示 逐元素乘法（element-wise multiplication）。
GELU（Gaussian Error Linear Unit）是一个非线性激活函数，它与ReLU激活函数类似，但它比 ReLU 更平滑，适用于深度模型。

特性	ReLU	GELU	SwiGLU with GELU
表达能力	线性激活，易丢失负值信息	平滑激活，但无门控机制	动态门控，表达能力最强
梯度流动	负值梯度为 0，可能导致死神经元	平滑梯度流动	更平滑的梯度流动，训练更稳定
训练效率	计算简单，但可能不稳定	计算稍复杂，但效果更好	高效计算，适合大规模模型

门控机制通过逐元素乘法和动态调控，使模型能够高效选择性地传递信息，避免了简单线性流程中的冗余计算和信息丢失问题。相比于传统的线性层，门控机制不仅提高了计算效率，还增强了模型的非线性表达能力和训练稳定性，使其在 NLP 和计算机视觉等复杂任务中表现更加优异。

在实际实现LLaMA架构的时候，LLaMA官方使用了SILU激活函数。SiLU(Sigmoid-Weighted Linear Unit)是一种平滑的非线性激活函数，具有较好的梯度流动特性，常用于深度神经网络的激活层中。
SiLU ( x ) = x ⋅ σ ( x ) = x ⋅ 1 1 + e − x \text{SiLU}(x) = x \cdot \sigma(x) = x \cdot \frac{1}{1 + e^{-x}} SiLU(x)=x⋅σ(x)=x⋅1+e−x1
SiLU 的导数（梯度） ：
d d x SiLU ( x ) = σ ( x ) + x ⋅ σ ( x ) ⋅ ( 1 − σ ( x ) ) \frac{d}{dx} \text{SiLU}(x) = \sigma(x) + x \cdot \sigma(x) \cdot (1 - \sigma(x)) dxdSiLU(x)=σ(x)+x⋅σ(x)⋅(1−σ(x))

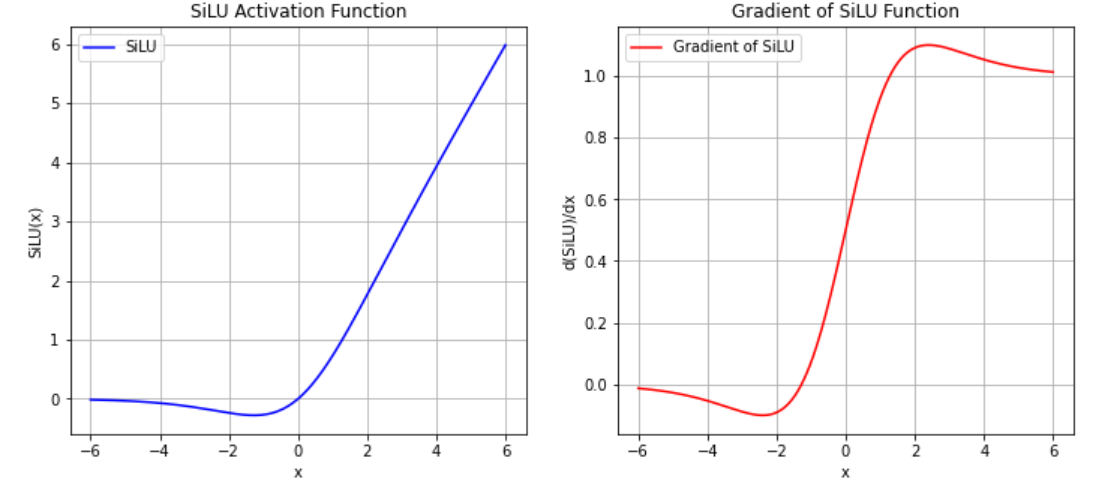
特性	ReLU	GELU	SiLU
平滑性	不平滑	平滑	平滑
负值处理	输出 0	有负值输出	更加平滑的负值输出
梯度流动	负值区域无梯度	平滑梯度流动	全范围平滑梯度流动
表达能力	适中	强	强，且自适应线性/非线性
计算复杂度	低	较高	适中

在LLaMA的前馈神经网络中实现的实际上是

SwiGLU with Silu
Output = Linear2 ( Silu ( Linear1 ( x ) ) ⊙ Linear3 ( x ) ) \text{Output} = \text{Linear2} \left( \textcolor{red}{\text{Silu}}\left( \textcolor{green}{\text{Linear1}}(x) \right) \odot \textcolor{gold}{\text{Linear3}}(x) \right) Output=Linear2(Silu(Linear1(x))⊙Linear3(x))

python 复制代码

class FeedForward(nn.Module):
    def __init__(self, dim: int, hidden_dim: int, multiple_of: int, dropout: float):
        super().__init__()
        if hidden_dim is None:
        		# Step 1: 设置初始值，通常为输入维度的 4 倍
            hidden_dim = 4 * dim
            # Step 2: 缩减到 2/3 的大小
            hidden_dim = int(2 * hidden_dim / 3)
            # Step 3: 对齐 multiple_of
            hidden_dim = multiple_of * ((hidden_dim + multiple_of - 1) // multiple_of)
        self.w1 = nn.Linear(dim, hidden_dim, bias=False)
        self.w2 = nn.Linear(hidden_dim, dim, bias=False)
        self.w3 = nn.Linear(dim, hidden_dim, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.dropout(self.w2(F.silu(self.w1(x)) * self.w3(x)))

5.2 FFN加入混合专家网络

5.2.1 MOE简介

门控机制通过一个线性层的输出控制另一个线性层的信息传递，从而筛选关键信息。在SwiGLU激活函数中，这一过程表现为：
SwiGLU ( x ) = GELU ( W 1 a ⋅ x ) ⊙ W 1 b ⋅ x \text{SwiGLU}(x) = \textcolor{red}{\text{GELU}}\left( \textcolor{green}{W_1^a} \cdot x \right) \odot \textcolor{gold}{W_1^b} \cdot x SwiGLU(x)=GELU(W1a⋅x)⊙W1b⋅x
其中，绿色路径负责信息传递，金色路径作为门控单元压缩数据通路。
基于这一机制，混合专家模型（Mixture of Experts, MOE）通过引入多个并行门控单元扩展了单一门控的局限性。
MOE架构包含多个专家网络和动态路由机制，能够根据输入特征选择性地激活不同专家组合。这种设计使模型能够同时处理多类重要信息，类似于卷积神经网络的多卷积核机制或注意力机制的多头结构。混合专家模型的核心优势在于其参数高效性和动态计算能力。
MoE 在每次前向传播时只激活部分专家模型，从而实现参数高效和计算高效。

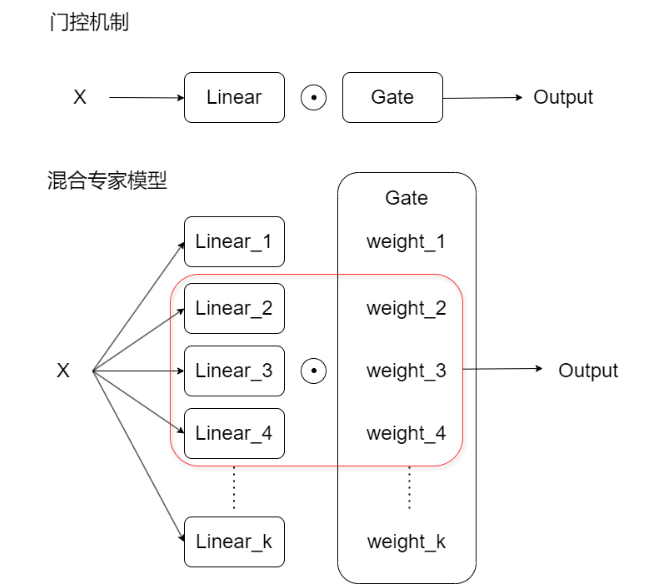
路由器是多个门构成的结构，用于控制信息的流程。动态路由策略是一种在深度学习模型中使用的技术，其核心思想是：根据输入数据的特征动态地选择路径或专家模型来处理信息。与传统模型固定的前向传播路径不同，动态路由策略在每次前向传播时，根据输入的情况选择最合适的子网络、路径或专家来处理数据。这大幅提升了模型的灵活性、计算效率和泛化能力。
MoE 的核心公式：
Output = ∑ i = 1 N G i ( x ) ⋅ E i ( x ) \text{Output} = \sum_{i=1}^N G_i(x) \cdot E_i(x) Output=i=1∑NGi(x)⋅Ei(x)
E i ( x ) E_i(x) Ei(x) ：第 i i i 个专家模型的输出。
G i ( x ) G_i(x) Gi(x)：由路由器（Gate）计算得到的权重，决定哪些专家应该被激活、每个专家被激活的程度有多大。
N：专家模型的总数。通常来说，我们不会采用全部的专家的结果，而是采用权重最大的top-k个专家的结果，因此在实际计算时，N往往会被k所替代。
主要组件：

专家模型（Experts）：多个全连接层或其他子模型，每个专家处理输入的不同部分或模式。
路由器（Router/Gate）：为每个输入选择合适的专家（可以是一个或多个），并为每个被选中的专家分配权重。
Sparse Activation ：每次计算时，只激活少数几个专家，大幅减少计算开销。在实际计算中，路由器（Gate）不会为所有专家分配非零权重，而是选择Top-k 个权重最高的专家激活。未被激活的专家（即 Top-k 之外的专家）的输出将不会参与计算，它们的权重 G i ( x ) G_i(x) Gi(x)会是0。

MOE作为很好的输出模型，可以用于代替Transformer中的前馈网络（FFN）层。优势在于提高模型的表达能力，增强泛化能力，虽然参数量高，但计算时只激活部分参数，计算量低，有助于更有效的计算资源利用。

MOE取代FFN层后，在训练时，模型需要不断调整所有专家的参数，并保证路由器能够学会为不同输入选择合适的专家。因此，训练过程比推理要复杂得多，需要更多的计算资源和优化。

5.2.2 MOE训练和推理过程

MOE训练流程

输入数据准备 ：输入数据通过模型的编码层或其他层，产生隐状态 (hidden states)，作为路由器和专家模型的输入。
路由器（Gate）计算权重 ：路由器根据输入数据，计算每个专家的激活权重 。使用 softmax 或其他激活函数计算每个专家的得分（G_i(x)），然后通过 top-k 筛选出权重最大的专家。
选择 Top-k 专家 ：使用 torch.topk() 函数，选择 top-k 个得分最高的专家。只有这 k 个专家参与向前传播的计算，其他专家的输出会被忽略（权重为 0）。
专家计算输出 ：被选中的 Top-k 专家根据输入数据计算它们的输出。路由器的权重用于对这些输出进行加权求和。
损失计算与辅助损失（Auxiliary Loss） ：除了常规损失（如交叉熵），还引入辅助损失，确保所有专家都能被均衡使用，避免某些专家"过度使用"或"闲置"。
反向传播与参数更新 ：使用反向传播更新所有专家的参数，以及路由器的参数。即使某些专家在当前 batch 中未被激活，它们的参数也可能因为累积梯度而被更新。

注意，在一次前向传播中，未被激活的专家不会参与计算，因此它们的梯度也不会直接更新。但是，模型通常会在多个 batch 或不同输入中均衡地激活不同的专家，因此所有专家的参数会在整个训练过程中得到更新。

在混合专家模型 (MoE) 中，由于其稀疏激活机制，专家的选择并非针对于整个批次的整体输出，而是针对每个 token（或时间步）进行选择和计算的。这也是一个专家的激活频率是基于每个 token 或每个时间步来统计的原因。

在引入 MoE 后，模型会为每个 token 或每个时间步单独计算路由器输出，从而决定该 token 应该使用哪些专家。这意味着：

每个 token 或每个位置的计算会激活不同的专家。
每个专家在同一批次的不同 token 上可能会被多次激活。

因此，在 MoE 中，专家的选择是基于每个 token 进行的，而不是基于整个序列或批次。

MoE推理流程

输入数据通过路由器 ：输入数据经过路由器，路由器根据当前输入，计算每个专家的得分（G_i(x)）。
激活 Top-k 专家：路由器选择 Top-k 个得分最高的专家，并忽略其他专家。
Top-k 专家输出计算 ：只有这 Top-k 个专家参与计算，其他专家的输出为 0，减少了计算开销。
加权求和得到最终输出：路由器对这 Top-k 个专家的输出进行加权求和，得到模型的最终输出。

阶段	训练	推理
激活专家数	Top-k 专家参与计算，但所有专家更新参数	只激活 Top-k 专家，其他专家不计算
反向传播	需要反向传播和梯度计算	不需要梯度计算
内存占用	高（需要存储所有专家的参数和梯度）	低（只需要存储部分专家的输出）
计算量	高（所有专家的梯度都可能被更新）	低（只计算部分专家的输出）
负载均衡	需要负载均衡，避免专家使用不均	不需要，因为只需一次前向传播
跨设备通信	需要频繁的跨设备通信	通信需求较低

5.2.3 MOE瓶颈问题和辅助损失机制

少数专家成为"瓶颈 "是混合专家模型 (MoE) 中常见的问题之一。在 MoE 中，路由器（Gate）会为每个输入选择一部分专家（如 Top-k 个）来处理当前任务。然而，由于数据分布不均或路由器的偏向性、以及训练的偶然性，实际中可能会出现以下几种情况：

专家的偏向性：由于路由器的训练偏差，某些专家会被频繁激活，而其他专家几乎从不被使用。
激活不均衡：一些专家会承载大部分计算负担，而其他专家却"闲置"，无法获得足够的训练机会。
参数更新不充分：未被激活的专家参数得不到更新，导致这些专家无法在模型训练中发挥作用。

这样的情况被称为"专家瓶颈"，这可能导致------

负载不均衡：瓶颈专家承载过多的计算负担，而其他专家闲置，导致模型整体计算资源未能高效利用。
训练效果下降 ：频繁被激活的专家过度训练，可能出现过拟合，而其他专家则由于长期未被激活导致参数更新不足，导致模型的泛化能力下降。
模型退化：随着训练的进行，未被激活的专家无法学习到有用的特征，进而降低整个模型的表现。

为了解决专家瓶颈 问题，通常引入一种称为辅助损失（Auxiliary Loss）的机制，用来均衡专家的使用频率 ，确保所有专家都能在训练中获得足够的激活机会。这种辅助损失会被叠加在神经网络的主要损失（如交叉熵损失、MSE 等）上，它在训练过程中与主要损失一起影响模型的反向传播和参数更新。这种设计确保模型在优化主要任务的同时，也能够实现一些额外的目标，比如均衡专家的使用频率、提升模型的泛化能力。当存在辅助损失时，总损失的计算公式为：
Total Loss = Main Loss + α ⋅ Auxiliary Loss \text{Total Loss} = \text{Main Loss} + \alpha \cdot \text{Auxiliary Loss} Total Loss=Main Loss+α⋅Auxiliary Loss

其中 α \alpha α是用来控制平衡的超参数。

在 MoE 模型中，常见的 MoE 辅助损失函数如下：

负载平衡损失 (Load Balancing Loss) ：促进不同专家的负载更加平衡，避免过度依赖某个专家。一种常见的形式是使用专家的选择频率与分配的均衡性来构造。通常，目标是让每个专家的选择概率与理想的均匀分布更接近。
aux_loss = ∑ i = 1 N f i log ⁡ ( f i ) \text{aux\loss} = \sum{i=1}^{N} f_i \log(f_i) aux_loss=i=1∑Nfilog(fi)

其中 f i f_i fi 是第 i i i 个专家被选择的频率。
基于熵的损失 (Entropy-based Loss) ：通过增加专家选择的熵，鼓励模型选择更多的专家来参与计算，从而减少某些专家的过载。
aux_loss = − ∑ i = 1 N P i log ⁡ ( P i ) \text{aux\loss} = - \sum{i=1}^{N} P_i \log(P_i) aux_loss=−i=1∑NPilog(Pi)

其中 P i P_i Pi 是分配给第 i i i 个专家的概率。熵越高，说明分配越均匀。
KL 散度损失 (KL Divergence Loss) ：将实际的专家选择分布与理想的均匀分布进行比较。
aux_loss = KL ( P ∣ ∣ U ) \text{aux\_loss} = \text{KL}(P || U) aux_loss=KL(P∣∣U)

其中 $P$ 是模型计算出的专家分配概率分布， U U U 是理想的均匀分布。通过最小化 KL 散度，确保专家选择接近均匀分布，避免某些专家被过度使用。
专家负载正则化 (Expert Load Regularization) ：控制每个专家的负载，使得负载接近于模型的理想目标负载，比如让每个专家处理相同数量的样本。
aux_loss = ∑ i = 1 N ( load i − target_load ) 2 \text{aux\loss} = \sum{i=1}^{N} (\text{load}_i - \text{target\_load})^2 aux_loss=i=1∑N(loadi−target_load)2

其中 load i \text{load}_i loadi 是第 i i i 个专家的实际负载， target_load \text{target\_load} target_load 是理想的负载。

实际使用的损失函数
aux_loss = α × ∑ i = 1 N routed_experts ( P i ⋅ f i ) \text{aux\loss} = \alpha \times \sum{i=1}^{N_{\text{routed\_experts}}} (P_i \cdot f_i) aux_loss=α×i=1∑Nrouted_experts(Pi⋅fi)
N routed_experts N_{\text{routed\_experts}} Nrouted_experts 是专家的数量。
P i P_i Pi 是所有专家的平均权重。
f i f_i fi 是专家的平均使用率。
最后的辅助损失是所有专家的分配概率和使用频率乘积的加权求和，用参数 α \alpha α 来缩放损失。

5.2.4 MoE模型的具体实现

python 复制代码

import torch
import torch.nn as nn
import torch.nn.functional as F
import math

class MoEGate(nn.Module):
    def __init__(self, config: LMConfig):
        """
        初始化 MoEGate 类，用于混合专家模型中的门控机制。

        参数：
        - config: LMConfig 对象，包含模型的配置信息，如专家数量、得分函数、辅助损失等。
        """
        super().__init__()
        self.config = config  # 保存配置信息
        self.top_k = config.num_experts_per_tok  # 每次选择的 top-k 个专家数量
        self.n_routed_experts = config.n_routed_experts  # 总的专家数量

        self.scoring_func = config.scoring_func  # 路由器使用的得分函数（如 softmax）
        self.alpha = config.aux_loss_alpha  # 辅助损失的系数
        self.seq_aux = config.seq_aux  # 是否启用基于序列的辅助损失

        self.norm_topk_prob = config.norm_topk_prob  # 是否对 top-k 权重进行归一化
        # 每个专家被给与的权重的维度
        self.gating_dim = config.dim  # 输入维度
        # 路由器的权重矩阵：用于计算每个专家的得分
        self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))
        self.reset_parameters()  # 初始化权重参数

    def reset_parameters(self) -> None:
        """
        使用 Kaiming 初始化方法对权重矩阵进行初始化，确保模型在深层网络中有较好的梯度流动。
        """
        import torch.nn.init as init
        init.kaiming_uniform_(self.weight, a=math.sqrt(5))  # Kaiming 初始化

    def forward(self, hidden_states):
        """
        前向传播：根据输入的隐状态（hidden_states）计算专家的得分，选择 top-k 个专家，
        并在训练时计算辅助损失。

        参数：
        - hidden_states: Tensor，形状为 (batch_size, seq_len, hidden_dim) 的输入张量。

        返回：
        - topk_idx: 被选中的 top-k 个专家的索引。
        - topk_weight: 这些专家对应的权重。
        - aux_loss: 在训练模式下返回的辅助损失（否则为 None）。
        """
        # 获取 batch 大小、序列长度和隐藏维度
        bsz, seq_len, h = hidden_states.shape

        # 将输入重塑为二维张量 (batch_size * seq_len, hidden_dim)
        hidden_states = hidden_states.view(-1, h)

        # 使用线性层计算每个专家的得分，token-level (n_routed_experts, gating_dim) -> (batch_size * seq_len, n_routed_experts)
        logits = F.linear(hidden_states, self.weight, None)

        # 根据配置，使用 softmax 对得分进行归一化处理
        if self.scoring_func == 'softmax':
            scores = logits.softmax(dim=-1)  # 按照最后一维计算 softmax
        else:
            raise NotImplementedError(f'insupportable scoring function for MoE gating: {self.scoring_func}')

        # 获取 top-k 专家的权重和对应的索引
        topk_weight, topk_idx = torch.topk(scores, k=self.top_k, dim=-1, sorted=False)

        # 如果启用归一化，则对 top-k 权重进行归一化处理
        if self.top_k > 1 and self.norm_topk_prob:
            # 避免除以 0，添加小数项 1e-20
            denominator = topk_weight.sum(dim=-1, keepdim=True) + 1e-20
            topk_weight = topk_weight / denominator

        # 如果在训练模式下且辅助损失系数 alpha > 0，则计算辅助损失
        if self.training and self.alpha > 0.0:
            scores_for_aux = scores  # 获取所有专家的得分用于辅助损失计算
            aux_topk = self.top_k  # 辅助损失中使用的 top-k 专家数量
            # 将 top-k 专家的索引重塑为 (batch_size, top_k * seq_len)
            topk_idx_for_aux_loss = topk_idx.view(bsz, -1)

            if self.seq_aux:
                # 如果启用了序列级别的辅助损失
                scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1)

                # 初始化交叉熵损失的张量
                ce = torch.zeros(bsz, self.n_routed_experts, device=hidden_states.device)

                # 按照每个序列来计算，计算每个序列所对应的所有专家权重
                ce.scatter_add_(
                    1, topk_idx_for_aux_loss,
                    torch.ones(bsz, seq_len * aux_topk, device=hidden_states.device)
                ).div_(seq_len * aux_topk / self.n_routed_experts)

                # 计算序列级别的辅助损失
                aux_loss = (ce * scores_for_seq_aux.mean(dim=1)).sum(dim=1).mean() * self.alpha
            else:
                # 如果没有启用序列级别的辅助损失
                # 使用 one-hot 编码标记被选中的专家
                mask_ce = F.one_hot(topk_idx_for_aux_loss.view(-1), num_classes=self.n_routed_experts)
                ce = mask_ce.float().mean(0)  # 计算每个专家的平均使用率

                Pi = scores_for_aux.mean(0)  # 所有专家的平均分配概率
                fi = ce * self.n_routed_experts  # 专家使用频率
                aux_loss = (Pi * fi).sum() * self.alpha  # 计算辅助损失
        else:
            aux_loss = None  # 如果不在训练模式或 alpha=0，则不计算辅助损失

        # 返回 top-k 专家的索引、对应权重和辅助损失
        return topk_idx, topk_weight, aux_loss

python 复制代码

import torch
import torch.nn as nn

class MOEFeedForward(nn.Module):
    def __init__(self, config: LMConfig):
        """
        初始化 MOEFeedForward 类。
        
        参数：
        - config: 包含模型配置的 LMConfig 对象，包括专家数量、维度、隐藏层维度和 dropout 参数。
        """
        super().__init__()
        self.config = config
        
        # 创建多个专家网络的列表 (ModuleList)，每个专家是一个 FeedForward 层
        self.experts = nn.ModuleList([
            FeedForward(
                dim=config.dim,
                hidden_dim=config.hidden_dim,
                multiple_of=config.multiple_of,
                dropout=config.dropout,
            )
            for _ in range(config.n_routed_experts)  # n_routed_experts：总专家数量
        ])

        # 创建门控 (Gate) 对象，用于选择哪些专家参与计算
        self.gate = MoEGate(config)

        # 如果配置指定了共享专家，则代表允许MoE与FeedForward并联
        if config.n_shared_experts is not None:
            self.shared_experts = FeedForward(
                dim=config.dim,
                hidden_dim=config.hidden_dim,
                multiple_of=config.multiple_of,
                dropout=config.dropout,
            )

    def forward(self, x):
        """
        前向传播逻辑。

        参数：
        - x: 输入张量，形状为 (batch_size, seq_len, hidden_dim)。

        返回：
        - y: 输出张量，经过专家网络和共享专家（如果存在）的计算。
        """
        identity = x  # 保存原始输入（用于后续的残差连接）
        orig_shape = x.shape  # 保存原始输入的形状信息
        bsz, seq_len, _ = x.shape  # 获取批次大小、序列长度和隐藏层维度

        # 使用门控机制选择参与计算的专家
        topk_idx, topk_weight, aux_loss = self.gate(x)  # topk_idx: 选中的专家索引，topk_weight: 选中的专家权重

        # 将输入数据重塑为 (batch_size * seq_len, hidden_dim)
        x = x.view(-1, x.shape[-1])  
        flat_topk_idx = topk_idx.view(-1)  # 将专家索引展平成一维

        if self.training:
            # 训练模式下，重复输入数据以适应专家数量
            x = x.repeat_interleave(self.config.num_experts_per_tok, dim=0)

            # 创建用于存储专家输出的张量
            y = torch.empty_like(x, dtype=torch.float16)

            # 遍历每个专家，将符合条件的 token 输入到对应专家中
            for i, expert in enumerate(self.experts):
                y[flat_topk_idx == i] = expert(x[flat_topk_idx == i])  # 仅处理属于该专家的 token

            # 计算每个 token 的加权输出
            y = (y.view(*topk_weight.shape, -1) * topk_weight.unsqueeze(-1)).sum(dim=1)
            y = y.view(*orig_shape)  # 恢复为原始输入的形状
        else:
            # 推理模式下，只选择最优专家
            y = self.moe_infer(x, flat_topk_idx, topk_weight.view(-1, 1)).view(*orig_shape)

        # 如果有共享专家，将共享专家的输出与 y 相加（残差连接）
        if self.config.n_shared_experts is not None:
            y = y + self.shared_experts(identity)

        return y

    @torch.no_grad()
    def moe_infer(self, x, flat_expert_indices, flat_expert_weights):
        """
        推理模式下的专家计算逻辑。

        参数：
        - x: 输入张量，形状为 (batch_size * seq_len, hidden_dim)。
        - flat_expert_indices: 展平后的专家索引，用于指示哪些 token 属于哪些专家。
        - flat_expert_weights: 展平后的专家权重，用于加权专家的输出。

        返回：
        - expert_cache: 经过专家计算后的输出张量。
        """
        # 创建一个与输入形状相同的张量，用于存储专家输出
        expert_cache = torch.zeros_like(x)

        # 对专家索引进行排序，以便批量处理属于同一专家的 token
        idxs = flat_expert_indices.argsort()

        # 计算每个专家需要处理的 token 数量，并累积求和以找到每个专家的范围
        tokens_per_expert = flat_expert_indices.bincount().cpu().numpy().cumsum(0)

        # 将排序后的索引映射回 token 的原始位置
        token_idxs = idxs // self.config.num_experts_per_tok

        # 遍历每个专家，处理属于该专家的 token
        for i, end_idx in enumerate(tokens_per_expert):
            # 获取每个专家的 token 范围
            start_idx = 0 if i == 0 else tokens_per_expert[i - 1]

            # 如果该专家没有处理任何 token，则跳过
            if start_idx == end_idx:
                continue

            # 获取该专家对象
            expert = self.experts[i]

            # 获取属于该专家的 token 索引和对应的 token
            exp_token_idx = token_idxs[start_idx:end_idx]
            expert_tokens = x[exp_token_idx]

            # 通过专家计算 token 的输出
            expert_out = expert(expert_tokens)

            # 使用专家的权重对输出进行加权
            expert_out.mul_(flat_expert_weights[idxs[start_idx:end_idx]])

            # 将加权后的输出累加到 expert_cache 中
            expert_cache.scatter_add_(0, exp_token_idx.view(-1, 1).repeat(1, x.shape[-1]), expert_out)

        return expert_cache

六 LLama架构小型完整实现

6.1 数据并行与模型并行

数据并行与模型并行的认识
- 数据并行：适用于将相同的模型副本应用于不同的数据切片上。如，有多块 GPU，数据并行会将输入数据批次切分成多个小批次，每个 GPU 上都运行相同的模型副本，同时处理不同的数据子集。这意每个设备都计算部分的梯度，然后将所有设备上的梯度汇总，从而对模型进行全局更新。
- 模型并行：适用于大的模型，模型并行通过将模型的不同部分分布在不同设备上来解决单个单个设备内存不足的限制。模型的不同层或不同的部分会在不同的 GPU 上进行前向和反向传播计算。通常，模型并行用于特别大的神经网络架构，如 Transformer 或 GPT 模型。

1. 架构中与并行相关的关键
- 模型定义 ：在设计模型时，需要确保支持并行化。模型的每一层都需要使用标准的 PyTorch 模块（例如 torch.nn.ModuleList）来定义，这样可以确保模型在多设备上运行时保持一致性。特别是每一层的输入和输出维度必须匹配，以便于在数据并行或模型并行时正确地传播数据和梯度。代码中通过 TransformerBlock 和 torch.nn.ModuleList 模块化模型结构，这种设计便于并行扩展。
- 支持并行化：确保模型的架构可以支持数据并行（Data Parallelism）和模型并行（Model Parallelism）。在定义时要保持各层输入输出尺寸的一致性，便于 DeepSpeed 进行分布式处理。
1. 与 DeepSpeed 和 Hugging Face 的结合
- 使用 Hugging Face 和 DeepSpeed 的配置文件 ：在与 Hugging Face 生态系统兼容时，通常需要使用或继承 Hugging Face 的 PreTrainedModel 类，并确保模型定义与配置文件（config 文件）相匹配。配置文件中需要定义诸如模型的层数、嵌入维度、注意力头数等超参数，确保 Hugging Face 的 Trainer 工具能够正确加载和使用模型。同时，DeepSpeed 允许你通过简化模型并行和梯度计算来进行高效的分布式训练，因此在配置文件中还需要与 DeepSpeed 兼容的设置，例如启用 zero_optim 或 activation checkpointing。
- 分布式数据并行（DDP） ：DeepSpeed 和 Hugging Face 的分布式训练依赖于 PyTorch 的 DistributedDataParallel（DDP）。DDP 通过在多个 GPU 上并行处理数据来加速训练。因此，模型的定义需要支持在多机或多 GPU 环境中运行，并且模型的前向和后向传播需要能够同时在多个设备上进行。还需要结合 PyTorch 的 torch.distributed.init_process_group() 来初始化分布式进程，确保训练过程中的同步。
1. 权重初始化与保存
  在分布式训练中，模型的保存和加载方式略有不同，特别是当使用 DeepSpeed 时，模型的检查点（checkpoint）保存和恢复需要使用其专用 API。如，DeepSpeed 提供 deepspeed.save_checkpoint 和 deepspeed.load_checkpoint 函数，以确保模型参数和优化器状态在分布式环境下正确存储和恢复。在初始化权重时使用特定的初始化策略，如对 wo.weight 和 w3.weight 的正态分布初始化，有助于保证模型的训练收敛性。

6.2 具体的实现代码

配置文件内容

python 复制代码

from transformers import PretrainedConfig
from typing import List


class LMConfig(PretrainedConfig):
    model_type = "MateConv_LlaMA"

    def __init__(
            self,
            dim: int = 512,
            n_layers: int = 8,
            n_heads: int = 16,
            n_kv_heads: int = 8,
            vocab_size: int = 6400,
            hidden_dim: int = None,
            multiple_of: int = 64,
            norm_eps: float = 1e-5,
            max_seq_len: int = 512,
            dropout: float = 0.0,
            flash_attn: bool = True,
            use_moe: bool = False,
            num_experts_per_tok=2,
            n_routed_experts=4,
            n_shared_experts: bool = True,
            scoring_func='softmax',
            aux_loss_alpha=0.01,
            seq_aux=True,
            norm_topk_prob=True,
            **kwargs,
    ):
        self.dim = dim
        self.n_layers = n_layers
        self.n_heads = n_heads
        self.n_kv_heads = n_kv_heads
        self.vocab_size = vocab_size
        self.hidden_dim = hidden_dim
        self.multiple_of = multiple_of
        self.norm_eps = norm_eps
        self.max_seq_len = max_seq_len
        self.dropout = dropout
        self.flash_attn = flash_attn
        self.use_moe = use_moe
        self.num_experts_per_tok = num_experts_per_tok  # 每个token选择的专家数量
        self.n_routed_experts = n_routed_experts  # 总的专家数量
        self.n_shared_experts = n_shared_experts  # 共享专家
        self.scoring_func = scoring_func  # 评分函数，默认为softmax
        self.aux_loss_alpha = aux_loss_alpha  # 辅助损失的alpha参数
        self.seq_aux = seq_aux  # 是否在序列级别上计算辅助损失
        self.norm_topk_prob = norm_topk_prob  # 是否标准化top-k概率
        super().__init__(**kwargs)

python 复制代码

class TransformerBlock(nn.Module):
    def __init__(self, layer_id: int, args: LMConfig):
        """
        TransformerBlock 是 Transformer 模型的基础构件，包含自注意力机制、前馈网络，并根据配置使用 Mixture of Experts (MoE) 或常规前馈网络。

        参数：
        - layer_id: 当前层的编号，用于标识层。
        - args: LMConfig 配置类，包含模型的超参数配置，如注意力头数、维度等。
        """
        super().__init__()
        self.n_heads = args.n_heads  # 注意力头的数量
        self.dim = args.dim  # 总的模型维度
        self.head_dim = args.dim // args.n_heads  # 每个注意力头的维度
        self.attention = Attention(args)  # 自注意力机制模块

        self.layer_id = layer_id  # 当前层的编号
        self.attention_norm = RMSNorm(args.dim, eps=args.norm_eps)  # 注意力层前的 RMS 归一化
        self.ffn_norm = RMSNorm(args.dim, eps=args.norm_eps)  # 前馈网络层前的 RMS 归一化

        # 根据配置判断是否使用 Mixture of Experts (MoE) 作为前馈网络
        if args.use_moe:
            self.feed_forward = MOEFeedForward(args)  # 使用 Mixture of Experts (MoE) 前馈网络
        else:
            self.feed_forward = FeedForward(  # 使用常规的前馈网络
                dim=args.dim,  # 模型的总维度
                hidden_dim=args.hidden_dim,  # 前馈网络隐藏层的维度
                multiple_of=args.multiple_of,  # 隐藏层维度应为该数的倍数
                dropout=args.dropout,  # dropout 概率，用于正则化
            )

    def forward(self, x, pos_cis, kv_cache=False):
        """
        TransformerBlock 的前向传播函数。

        参数：
        - x: 输入张量。
        - pos_cis: 位置嵌入或旋转嵌入，用于加入位置信息。
        - kv_cache: 是否使用键值缓存（用于加速推理时）。

        返回：
        - out: Transformer Block 的输出张量。
        """
        # 输入经过注意力归一化后通过自注意力层，并叠加输入
        h = x + self.attention(self.attention_norm(x), pos_cis, kv_cache)
        # 注意力层输出经过前馈网络归一化后通过前馈网络，并叠加输出
        out = h + self.feed_forward(self.ffn_norm(h))
        return out  # 返回最终输出

python 复制代码

class Transformer(PreTrainedModel):
    config_class = LMConfig  # 定义模型使用的配置类
    last_loss: Optional[torch.Tensor]  # 用于记录最后计算的损失值

    def __init__(self, params: LMConfig = None):
        """
        Transformer 是一个基于 Transformer 架构的语言模型，继承自 PreTrainedModel。

        参数：
        - params: 配置对象 LMConfig，包含模型的超参数配置。
        """
        super().__init__(params)
        if not params:
            params = LMConfig()  # 如果没有提供配置，则使用默认配置
        self.params = params  # 保存模型参数配置
        self.vocab_size = params.vocab_size  # 词汇表大小
        self.n_layers = params.n_layers  # Transformer 的层数

        self.tok_embeddings = nn.Embedding(params.vocab_size, params.dim)  # 词嵌入层
        self.dropout = nn.Dropout(params.dropout)  # Dropout 层用于正则化
        self.layers = torch.nn.ModuleList()  # TransformerBlock 的容器
        for layer_id in range(self.n_layers):
            self.layers.append(TransformerBlock(layer_id, params))  # 逐层添加 TransformerBlock
        self.norm = RMSNorm(params.dim, eps=params.norm_eps)  # 最后的 RMS 正则化
        self.output = nn.Linear(params.dim, params.vocab_size, bias=False)  # 输出层，线性映射到词汇表大小
        self.tok_embeddings.weight = self.output.weight  # 共享词嵌入层和输出层的权重
        pos_cis = precompute_pos_cis(self.params.dim // self.params.n_heads, self.params.max_seq_len)
        self.register_buffer("pos_cis", pos_cis, persistent=False)  # 注册位置嵌入（或旋转嵌入），不参与训练

        self.apply(self._init_weights)  # 初始化模型权重

        # 特殊初始化部分参数权重
        for pn, p in self.named_parameters():
            if pn.endswith('w3.weight') or pn.endswith('wo.weight'):
                torch.nn.init.normal_(p, mean=0.0, std=0.02 / math.sqrt(2 * params.n_layers))

        self.last_loss = None  # 初始化最后的损失为 None
        self.OUT = CausalLMOutputWithPast()  # 初始化输出类
        self._no_split_modules = [name for name, _ in self.named_modules()]  # 保存不拆分的模块名称

    def _init_weights(self, module):
        """
        初始化模块权重。
        - 对线性层使用正态分布初始化权重，均值为 0，标准差为 0.02。
        - 对词嵌入层也使用正态分布初始化权重，均值为 0，标准差为 0.02。
        """
        if isinstance(module, nn.Linear):
            torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)
            if module.bias is not None:
                torch.nn.init.zeros_(module.bias)  # 如果存在偏置，将偏置初始化为 0
        elif isinstance(module, nn.Embedding):
            torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)

    def forward(self, tokens: Optional[torch.Tensor] = None, targets: Optional[torch.Tensor] = None,
                kv_cache=False, **keyargs):
        """
        Transformer 的前向传播函数。

        参数：
        - tokens: 输入的 token 张量，表示输入的词序列。
        - targets: 目标张量，用于计算交叉熵损失。
        - kv_cache: 是否使用键值缓存（用于加速推理）。
        - keyargs: 其他可选参数，如 'input_ids' 和 'attention_mask'。

        返回：
        - 输出的 logits 和 loss（如果有目标）。
        """
        current_idx = 0  # 当前索引初始化为 0
        if 'input_ids' in keyargs:
            tokens = keyargs['input_ids']  # 从关键字参数中提取 'input_ids'
        if 'attention_mask' in keyargs:
            targets = keyargs['attention_mask']  # 从关键字参数中提取 'attention_mask'
        if 'current_idx' in keyargs:
            current_idx = int(keyargs['current_idx'])  # 更新当前索引

        _bsz, seqlen = tokens.shape  # 获取输入 tokens 的 batch 大小和序列长度
        h = self.tok_embeddings(tokens)  # 将输入 tokens 通过词嵌入层进行嵌入
        h = self.dropout(h)  # 通过 dropout 进行正则化
        pos_cis = self.pos_cis[current_idx:current_idx + seqlen]  # 获取当前位置的旋转嵌入

        # 逐层通过 TransformerBlock
        for idx, layer in enumerate(self.layers):
            h = layer(h, pos_cis, kv_cache)  # 调用每个 TransformerBlock 的前向传播

        h = self.norm(h)  # 最后的 RMS 正则化处理

        if targets is not None:
            logits = self.output(h)  # 通过线性输出层生成 logits
            # 计算交叉熵损失，忽略 index 为 0 的位置，reduction 为 'none'，即不自动求平均
            self.last_loss = F.cross_entropy(logits.view(-1, logits.size(-1)), targets.view(-1),
                                             ignore_index=0, reduction='none')
        else:
            logits = self.output(h[:, [-1], :])  # 如果没有目标，只返回最后一个时间步的 logits
            self.last_loss = None  # 没有损失

        self.OUT.__setitem__('logits', logits)  # 设置输出的 logits
        self.OUT.__setitem__('last_loss', self.last_loss)  # 设置最后的 loss
        return self.OUT  # 返回输出对象

    @torch.inference_mode()
    def generate(self, idx, eos, max_new_tokens, temperature=0.7, top_k=8, stream=True, rp=1., kv_cache=True):
        """
        推理模式下的文本生成函数。

        参数：
        - idx: 输入的 tokens。
        - eos: 结束标志符号，当生成到 eos 时停止生成。
        - max_new_tokens: 最大生成的新 token 数量。
        - temperature: 控制生成的随机性，温度越高，生成越多样化。
        - top_k: 限制 top-k 采样，控制只选择概率最高的 k 个 token。
        - stream: 是否进行流式输出。
        - rp: 重复惩罚系数，控制重复 token 的惩罚。
        - kv_cache: 是否使用键值缓存来加速推理。

        返回：
        - 生成的 tokens（可能是流式返回）。
        """
        index = idx.shape[1]  # 获取输入 token 序列的长度
        init_inference = True  # 初始化推理标志
        while idx.shape[1] < max_new_tokens - 1:  # 当生成的 tokens 长度小于最大 tokens 数时继续生成
            if init_inference or not kv_cache:
                inference_res, init_inference = self(idx, kv_cache=kv_cache), False  # 第一次推理，或不使用缓存
            else:
                inference_res = self(idx[:, -1:], kv_cache=kv_cache, current_idx=idx.shape[1] - 1)  # 仅使用最后一个 token 推理

            logits = inference_res.logits  # 获取推理结果的 logits
            logits = logits[:, -1, :]  # 只选择最后一个 token 的 logits

            # 对生成的 token 进行重复惩罚
            for token in set(idx.tolist()[0]):
                logits[:, token] /= rp  # 对每个重复的 token 施加惩罚

            if temperature == 0.0:  # 如果温度为 0，使用贪心算法选择下一个 token
                _, idx_next = torch.topk(logits, k=1, dim=-1)
            else:
                logits = logits / temperature  # 根据温度调整 logits
                if top_k is not None:
                    v, _ = torch.topk(logits, min(top_k, logits.size(-1)))  # 使用 top-k 采样
                    logits[logits < v[:, [-1]]] = -float('Inf')  # 排除 top-k 之外的 logits

                probs = F.softmax(logits, dim=-1)  # 计算概率分布
                idx_next = torch.multinomial(probs, num_samples=1, generator=None)  # 根据概率进行采样

            if idx_next == eos:  # 如果生成了 eos token，停止生成
                break

            idx = torch.cat((idx, idx_next), dim=1)  # 将生成的 token 拼接到输入序列中
            if stream:  # 如果启用了流式输出
                yield idx[:, index:]  # 输出当前生成的 tokens

        if not stream:  # 如果未启用流式输出
            yield idx[:, index:]  # 返回生成的完整序列