**问题：**非齐次方程求解还要加上齐次方程的解是为了说明什么？Ax=0和AX=B，求的等式右边的向量都不同不多此一举吗？
答：非齐次方程的解加上对应的齐次方程的解，绝非多此一举，而是理解整个解集结构的关键。下面我通过一个表格和进一步的解释来帮您理清这里的逻辑。
| 对比维度 | 齐次方程组 Ax=0 | 非齐次方程组 Ax=b |
|---|---|---|
| 解的几何意义 | 解构成一个经过原点的向量空间（平面、直线等）。 | 解构成一个不经过原点 的平面/直线，是齐次解空间的平移。 |
| 解的结构 | 通解 = 基础解系的线性组合：xh=k1ξ1+...+kn−rξn−r | 通解 = 一个特解 + 齐次通解：x=xp+xh |
| 角色与功能 | 描述了系统固有的、由矩阵 A本身决定的所有可能的"运动"或"变化"方向（自由度）。 | 特解 xp是"锚点"，指明了平移的位置。齐次解 xh描述了围绕这个锚点所有可能的位置。 |
深入理解解的结构
这个"特解+齐次通解"的结构（x=xp+xh）揭示了两个方程解集之间的深刻联系。
-
平移关系 ：非齐次方程 Ax=b的任意一个解 ，都与齐次方程 Ax=0的某一个解 相差一个固定的向量（即特解 xp）。从几何上看，这意味着非齐次方程的所有解点，都是由齐次方程的解空间整体"平移"特解 xp这个向量后得到的。
-
"差值是齐次解"：如果 xp1和 xp2都是 Ax=b的解（特解），那么它们的差 xp1−xp2一定是 Ax=0的解。这从代数上证明了非齐次方程的解集确实是齐次解集的一个平移。
为什么这不是多此一举？
您觉得"求的等式右边的向量都不同"，似乎是两个问题，但关键在于：我们关心的是 Ax=b全部的解。
-
特解 xp的作用 ：它只回答了"有没有解 "以及"一个具体的解是什么"这个问题。它把解集在空间中的位置确定了下来。
-
齐次通解 xh的作用 ：它回答了"如果有解，到底有多少个解 "以及"所有这些解长什么样子"的问题。它描述了以特解为"锚点"，解可以在哪些方向上自由变化。齐次方程基础解系的向量，就指明了这些自由度的方向。
所以，将两者相加 x=xp+xh，是为了完整地、毫无遗漏地描述非齐次方程组 Ax=b在有无穷多解时的整个解集。缺少任何一部分，得到的都不是通解。
一个简单的比喻
您可以这样想象：
-
齐次方程的解 Ax=0 ：像一个无限大、且一定经过你家客厅原点的平面。这个平面的倾斜度由矩阵 A决定。
-
非齐次方程的解 Ax=b ：像另一个无限大、但与上面那个平面平行 的平面。它不经过原点（因为b向量≠0向量）。
-
特解 xp ：就像是从原点指向这个新平面上的任意一点的箭头。
-
通解结构：新平面（非齐次解）上的任何一点，都可以通过先走到老平面（齐次解）上的某一点，再沿着特解的箭头方向移动到达。反之亦然。x=xp+xh正是这个路径的数学表达。
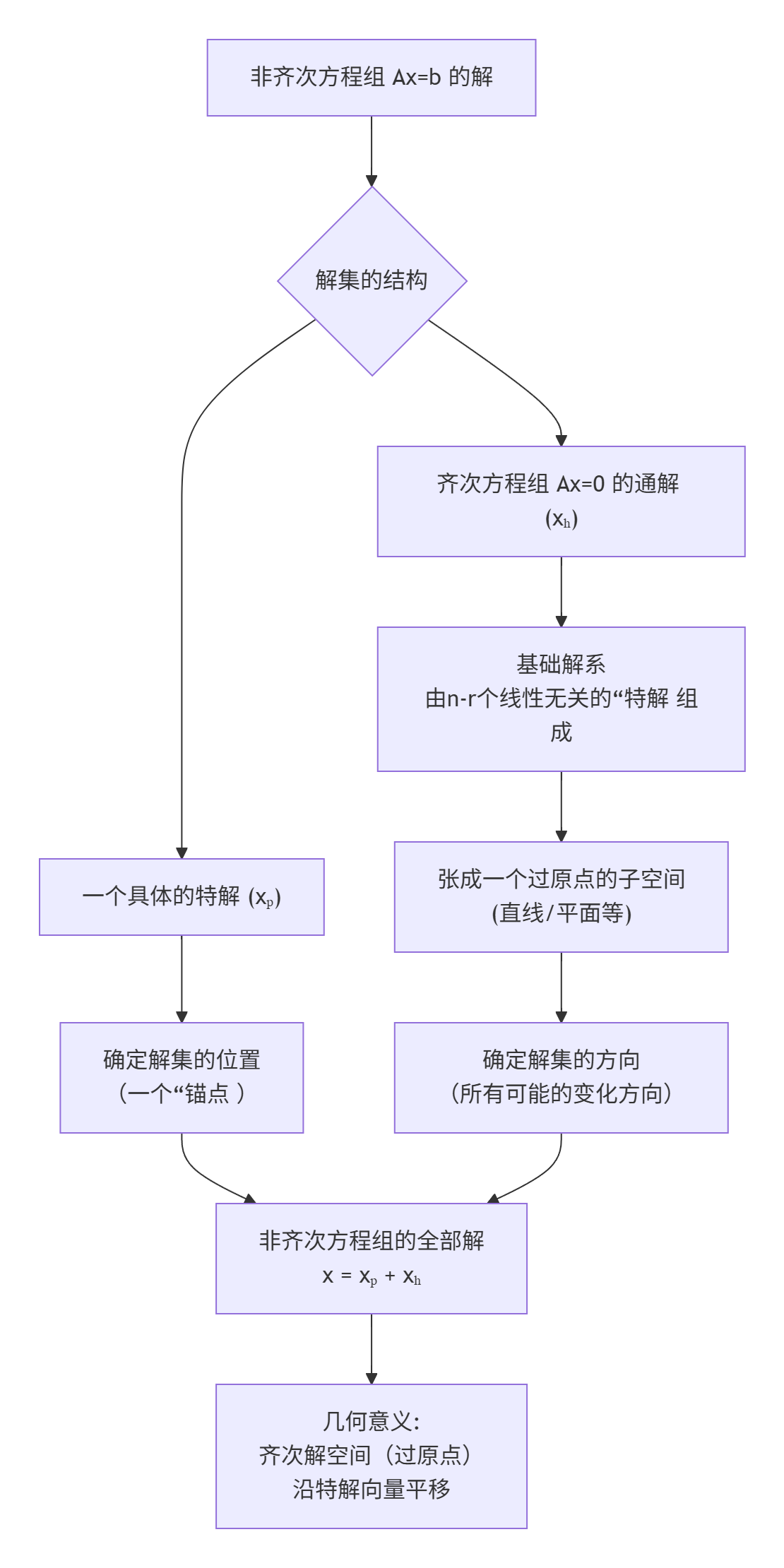图1-解集的结构
**再次尝试理解：**我是否能理解为齐次解构成一个二维平面，而特解提供了一个垂直于二维平面的向量，使得在平面内的向量和特解叠加可以映射到新的平面上去，而这些点的集合就构成了非齐次方程组的解空间？
答：你对线性方程组解的空间结构的理解方向是正确的，特别是关于"平移"的核心思想。不过，你描述中的一个小细节------"特解是一个垂直于二维平面的向量 "------这通常不是一个普遍成立的情况。让我用一个表格来梳理一下齐次和非齐次方程组解空间的核心关系，这能帮助我们更清晰地看到它们的异同。
| 对比维度 | 齐次方程组 Ax=0的解空间 | 非齐次方程组 Ax=b(b=0) 的解空间 |
|---|---|---|
| 几何结构 | 子空间（过原点，例如二维平面） | 仿射空间（不过原点，例如一个平行的平面） |
| 与原点关系 | 必过原点 | 不过原点（除非特解是零向量，但此时方程是齐次的） |
| 构成方式 | 基础解系的线性组合张成的空间 | 一个特解 (锚点) + 齐次解空间 (方向) |
| 空间关系 | - | 与非齐次解空间平行 ，是其平移的结果 |
🔍 理解"平移"的关键
现在我们来深入探讨一下"平移"这个概念，这有助于澄清你关于"垂直"的猜想。
-
"平移"的真正含义：特解 xp的作用，就像一个"搬运工"。它不是去改变齐次解空间（那个二维平面）本身的形状或方向，而是把它整体"搬"到一个新的位置。这个新位置就是由特解决定的。齐次解空间里的每一个点（向量），加上这个特解，就得到了非齐次方程组的一个解。所有这些新点构成的集合，就是一个与原平面平行、但不再经过原点的平面 。从代数上看，如果 v是齐次方程的任意解（即 Av=0），那么 xp+v一定是非齐次方程的解（即 A(xp+v)=b+0=b）。
-
为何通常不"垂直" ：特解向量 xp本身一般并不垂直于 齐次解空间（那个二维平面）。你可以这样想象：齐次解空间是一个过原点的平面，特解是空间中的一个点（从原点指向这个点的向量就是特解向量）。这个点决定了新平面的位置，但连接原点和新点的这条线（特解向量），其方向是任意的，并不一定要求是原平面的法线方向。特解的本质是提供一个"偏移"或"起点"，而不是一个"垂直"的方向。使得两个平面平行的关键，在于它们的内在"方向"完全由齐次方程的解（即矩阵A的零空间）决定 。
🧠 深入理解：为何特解不唯一，但解集唯一
你可能会有另一个疑问：如果特解是确定位置的"锚点"，但特解本身又不唯一（对于有无穷多解的非齐次方程组，我们可以找到无数个特解），这是否矛盾呢？
并不矛盾。关键在于：无论你选择哪一个特解作为"锚点"，最终得到的整个解集都是完全相同的。
我们可以这样理解：
-
假设 xp1和 xp2都是方程组 Ax=b的解（即两个不同的特解）。
-
根据解的性质，它们的差 xp1−xp2必然是对应齐次方程组 Ax=0的一个解。
-
这意味着，以 xp1为锚点的解集，和以 xp2为锚点，再将整个齐次解空间平移一个向量 (xp1−xp2)后得到的解集，是完全重合的。
所以，虽然特解可以任意选择，但它只是我们用来描述整个解集的一个便捷的"起点"或"代表"，解集本身是唯一确定的。
💎 最终总结与例子
1. 特解向量唯一确定了这个解集合在空间中的位置 。无论你选择哪一个特解作为"锚点"，最终得到的整个解集都是完全相同的 。（虽然特解可以任意选择，但它只是我们用来描述整个解集的一个便捷的"起点"或"代表"，解集本身是唯一确定的。）
2. 通解公式 x=xp+k1ξ1+k2ξ2+...的几何意义。即基础解系的线性组合上所有点与特解向量的叠加构成整个解集合"。
3. 齐次方程的解构成一个过原点的二维平面（或其他维度的子空间）。特解的作用不是提供一个垂直于该平面的向量，而是提供一个平移量，将这个平面整体"移动"到一个新的位置，从而形成一个与原平面平行但不过原点的新的"平面"（仿射空间）。这个移动后的空间，就是非齐次方程组的解空间。
这就好比在地图上，齐次解空间是所有以市政府为起点的道路网（过原点），而非齐次方程有解时，相当于告诉你一个具体的地址（特解）。整个道路网按照这个地址平移过去，就得到了目标地点周围的所有道路（非齐次解空间）。道路的走向（空间的方向）没变，只是位置移动了。