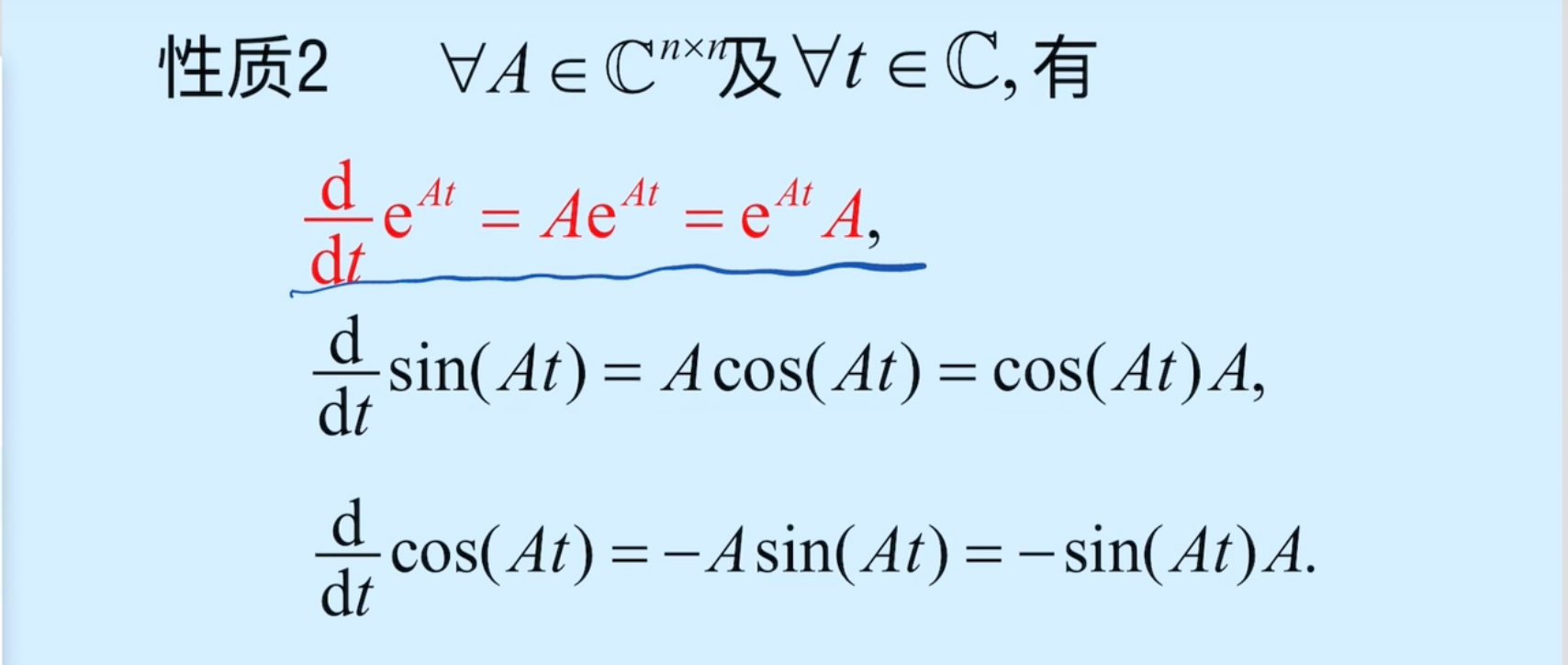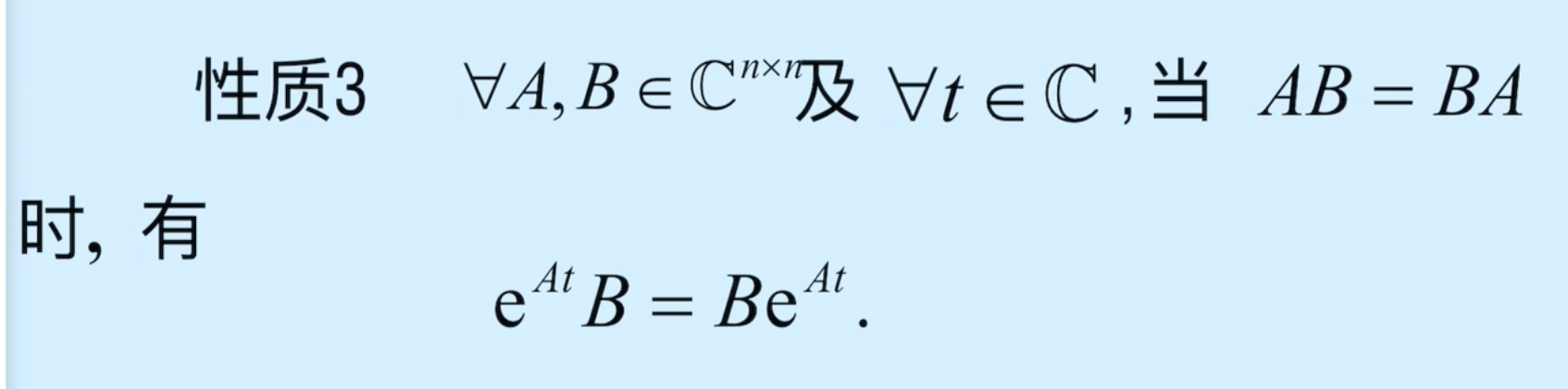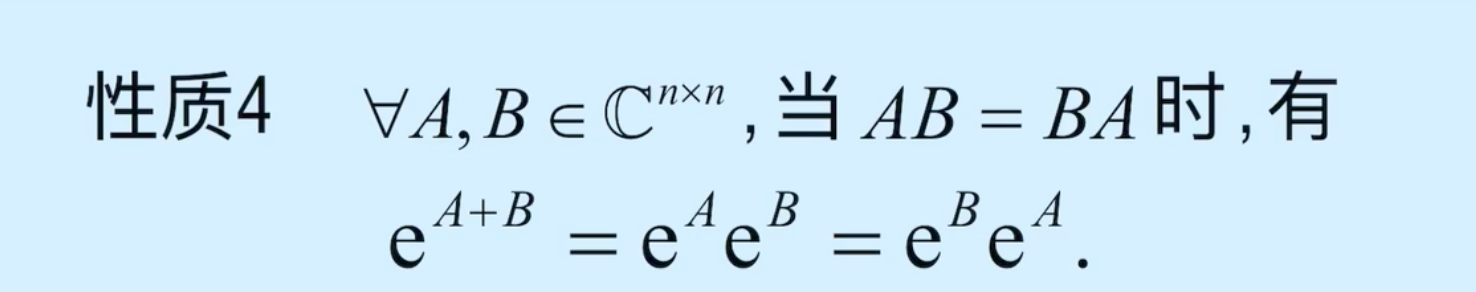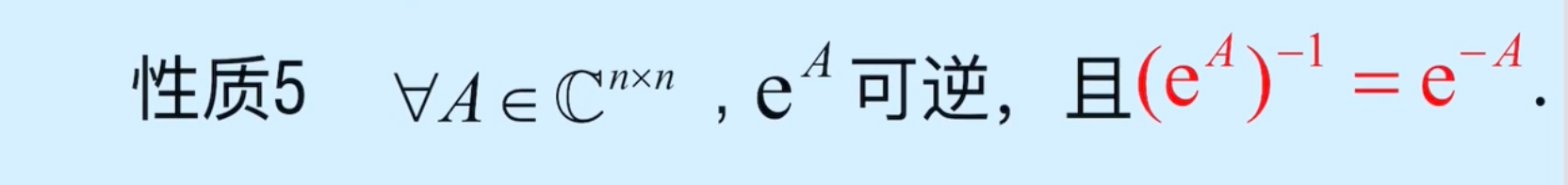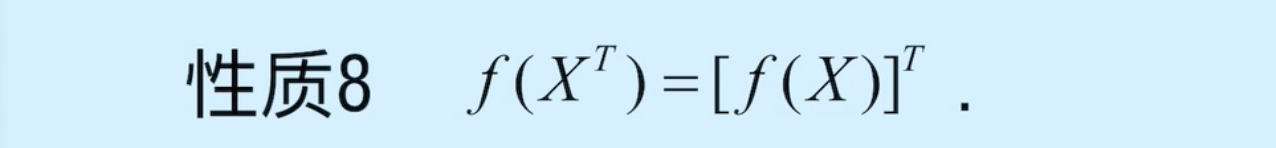矩阵分析 方阵幂级数与方阵函数
一、方阵幂级数
1、方阵幂级数概念
设 { c k } \{c_k\} {ck} 是复数列, ∀ X ∈ C n × n \forall X \in \mathbb{C}^{n \times n} ∀X∈Cn×n,称
∑ k = 0 ∞ c k X k = c 0 E + c 1 X + c 2 X 2 + ⋯ + c k X k + ⋯ \sum_{k=0}^{\infty} c_k X^k = c_0 E + c_1 X + c_2 X^2 + \cdots + c_k X^k + \cdots k=0∑∞ckXk=c0E+c1X+c2X2+⋯+ckXk+⋯
为方阵 X X X 的幂级数, c k c_k ck 称为第 k k k 项的系数。

2、方阵幂级数收敛概念
若当 X = A X=A X=A 时方阵级数
∑ k = 0 ∞ c k X k = c 0 E + c 1 X + c 2 X 2 + ⋯ + c k X k + ⋯ \sum_{k=0}^{\infty} c_k X^k = c_0 E + c_1 X + c_2 X^2 + \cdots + c_k X^k + \cdots k=0∑∞ckXk=c0E+c1X+c2X2+⋯+ckXk+⋯
收敛(或绝对收敛),其和记为 f ( A ) f(A) f(A),则称 ∑ k = 0 ∞ X k \sum_{k=0}^{\infty}X^k ∑k=0∞Xk 在点 A A A 处收敛(或绝对收敛)。

3、方阵幂级数收敛判定
设幂级数 ∑ k = 0 ∞ c k z k \sum_{k=0}^{\infty}c_kz^k ∑k=0∞ckzk 的收敛半径为 R R R, X ∈ C n × n X \in \mathbb{C}^{n \times n} X∈Cn×n 的谱半径为 ρ ( X ) \rho(X) ρ(X),则
- 当 ρ ( X ) < R \rho(X)<R ρ(X)<R 时,方阵幂级数绝对收敛
- 当 ρ ( X ) < R \rho(X)<R ρ(X)<R 时,方阵幂级数发散
收敛半径 R R R 的求解:
R = lim k → ∞ ∣ c k + 1 c k ∣ R=\lim_{k \to \infty}|\frac{c_{k+1}}{c_k}| R=k→∞lim∣ckck+1∣
推论三项这里实际上是利用的谱半径是方阵范数的下确界来推导出来的
例题:



这道题目本质上和上面的题目是一样的,令 B = E − A B=E-A B=E−A,就可以得到 ∥ B ∥ < 1 \|B\|<1 ∥B∥<1,那么 ρ ( B ) < 1 \rho(B) < 1 ρ(B)<1,所以幂级数收敛
并且可以按上面的步骤证明和函数为 A − 1 A^{-1} A−1


二、方阵函数
1、几个常用的方阵函数
通过麦克劳林展开式定义方阵函数:


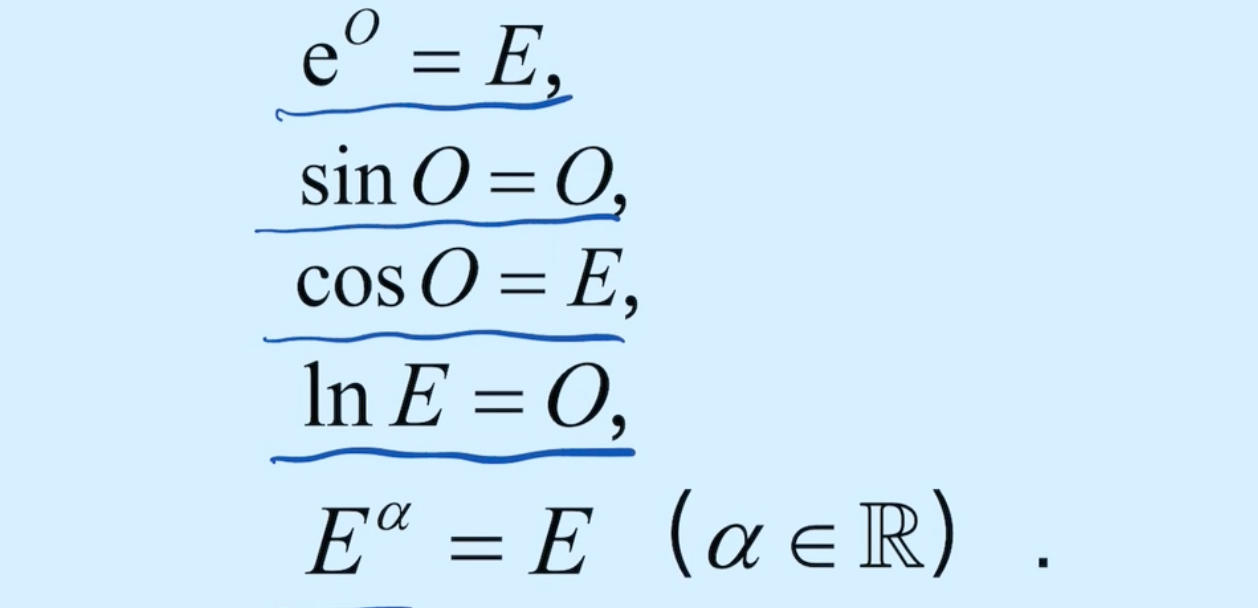
2、常见方阵函数的性质