在计算机视觉的世界里,我们经常讨论颜色、形状和边缘。但有一个维度,它比颜色更细腻,比形状更宏观,那就是------纹理(Texture)。
当你闭上眼摸一块丝绸和一块磨砂石,你能瞬间分辨出差异。但在数字图像里,这种"粗糙"与"平滑"的触感该如何量化?今天,我们就来聊聊纹理分析领域的大山:灰度共生矩阵(Gray-Level Co-occurrence Matrix,简称 GLCM)。
一、 为什么直方图"失灵"了?
在进入 GLCM 之前,我们先看一个直观的问题。
假设有两张图片:一张是整齐的棋盘格,另一张是完全随机的噪点图。如果计算它们的灰度直方图,你会发现它们可能完全一样。
- 直方图只关心:图像里有多少个 128 灰度级的像素?
- 直方图不关心:这些 128 的像素是在一起排队,还是乱七八糟地散落着?
直方图丢失了空间信息。 而 GLCM 的出现,就是为了把这种被丢掉的"空间排列规律"找回来。
二、 GLCM 的核心逻辑:数数像素的"社交圈"
GLCM 的核心思想非常朴素:它不再看单个像素,而是看"像素对"。
它会统计在图像中,相隔一定距离、沿一定方向的两个像素,它们的灰度值共同出现的频率。
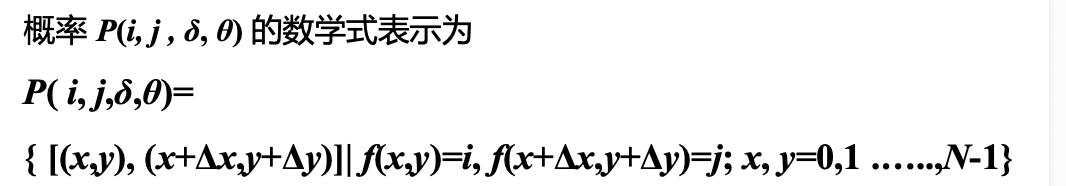
1. 三个关键参数(决定了你怎么"数")
- 距离 (δ\deltaδ):你想看多远的邻居?通常选 1 个像素。
- 角度 (θ\thetaθ):你想看哪个方向的邻居?标准动作通常是:0°(水平)、45°(右上)、90°(垂直)、135°(左上)。
- 灰度级 (LLL) :如果原始图像是 256 级,矩阵会达到 256×256256 \times 256256×256,太大了。通常我们会先将图像压缩到 8 级或 16 级。
2. 手把手演示计算过程
假设有一个 4x4 的微型图像,灰度只有 0-3:
0 1 0 1
1 0 1 0
2 2 3 3
2 2 3 3我们算 方向=0°(水平向右),距离=1 的 GLCM:
- 看 (0, 1) 这个组合:第一行出现了两次,第二行两次。总共 4 次。
- 看 (1, 0) 这个组合:第一行出现了一次,第二行一次。总共 2 次。
- 看 (2, 2) 和 (3, 3):在下面两行各出现了 2 次。
- 最终,你会填满一个 4x4 的 GLCM 矩阵。矩阵中数值越高的地方,代表这种灰度组合在空间上越密集。
三、 从矩阵到特征:著名的 Haralick 特征
GLCM 矩阵本身还是太庞大了(比如 16×1616 \times 1616×16)。为了让计算机更方便处理,1973 年,科学家 Haralick 建议从这个矩阵里再提取出几个数值。这就是我们常说的"二次统计"。
以下是最常用的四个"性格指标":
1. 对比度 (Contrast) ------ 纹理深不深?
它衡量矩阵中偏离对角线的程度。
- 如果相邻像素差值很大,对比度就高。
- 视觉效果:图像纹理沟壑深、边界清晰。
2. 能量 (Energy / ASM) ------ 纹理规不规整?
它是矩阵元素的平方和。
- 如果图像纹理非常整齐、周期性极强,GLCM 矩阵中只有少数几个地方数值极高,能量就大。
- 视觉效果:像整齐的编织物。
3. 熵 (Entropy) ------ 画面乱不乱?
它代表信息的随机性。
- 如果像素排列杂乱无章,GLCM 矩阵里的数值分布就会非常分散。
- 视觉效果:复杂的噪点、乱石堆。
4. 均匀性 (Homogeneity / 自相关) ------ 画面纯不纯?
衡量局部灰度变化的剧烈程度。
- 如果图像大面积平坦,像素对基本都落在对角线上。
- 视觉效果:平滑的皮肤、干净的天空。
四、 实战建议:如何用好 GLCM?
在实际项目(如医学影像分析、遥感地貌识别)中,单靠一个方向的 GLCM 是不够的。
- 旋转不变性 :通常我们会计算 0°、45°、90°、135° 四个方向的特征值,然后取它们的平均值作为该图像的最终特征。这样,即便旋转了图片,特征依然稳定。
- 尺度敏感性 :如果你想识别大块的纹理,尝试增大距离 δ\deltaδ。
- 计算加速:一定要做灰度压缩(例如降到 16 级),否则计算量会呈指数级上升,且容易产生稀疏矩阵,导致统计学意义失效。
五、 总结:GLCM 的现代价值
虽然现在的深度学习(CNN)可以自动提取特征,但 GLCM 依然没有过时。
在一些小样本数据、需要高解释性的医疗辅助诊断、或者算力受限的工业检测设备中,GLCM 凭借其计算速度快、物理意义明确的优势,依然是算法工程师武器库里的必备良药。
一句话总结 GLCM: 它不是在看颜色,而是在看像素之间如何"成群结队"地排布,从而把玄学的"触感"变成了科学的"概率"。
如果你对图像处理感兴趣,欢迎关注我的系列博文,下一期我们将聊聊 LBP(局部二值模式)是如何在人脸识别中大放异彩的!