单元函数矩阵微积分和多元向量值的导数
一、单元函数矩阵的微分
1、单元函数矩阵
以变量 t t t 的函数 a i j ( t ) a_{ij}(t) aij(t) 为元素的矩阵
A ( t ) = [ a i j ( t ) ] m × n = [ a 11 ( t ) a 12 ( t ) ⋯ a 1 n ( t ) a 21 ( t ) a 22 ( t ) ⋯ a 2 n ( t ) ⋮ ⋮ ⋮ a m 1 ( t ) a m 2 ( t ) ⋯ a m n ( t ) ] A(t) = [a_{ij}(t)]{m \times n} = \begin{bmatrix} a{11}(t) & a_{12}(t) & \cdots & a_{1n}(t) \\ a_{21}(t) & a_{22}(t) & \cdots & a_{2n}(t) \\ \vdots & \vdots & & \vdots \\ a_{m1}(t) & a_{m2}(t) & \cdots & a_{mn}(t) \end{bmatrix} A(t)=[aij(t)]m×n= a11(t)a21(t)⋮am1(t)a12(t)a22(t)⋮am2(t)⋯⋯⋯a1n(t)a2n(t)⋮amn(t)
称为单元函数矩阵。
2、求导
设 A ( t ) = [ a i j ( t ) ] m × n ( t ∈ C ) A(t) = [a_{ij}(t)]{m \times n} (t \in \mathbb{C}) A(t)=[aij(t)]m×n(t∈C),若 ∀ i = 1 , 2 , ⋯ , m , j = 1 , 2 , ⋯ , n , a i j ( t ) \forall i = 1,2,\cdots,m,j=1,2,\cdots,n,a{ij}(t) ∀i=1,2,⋯,m,j=1,2,⋯,n,aij(t) 都可导,则称 A ( t ) A(t) A(t) 可导,并且规定 A ( t ) A(t) A(t) 对变量 t t t 的导数为:
d A ( t ) d t = [ a i j ′ ( t ) ] m × n = [ a 11 ′ ( t ) a 12 ′ ( t ) ⋯ a 1 n ′ ( t ) a 21 ′ ( t ) a 22 ′ ( t ) ⋯ a 2 n ′ ( t ) ⋮ ⋮ ⋮ a m 1 ′ ( t ) a m 2 ′ ( t ) ⋯ a m n ′ ( t ) ] . \frac{\mathrm{d}A(t)}{\mathrm{d}t} = \left[ a'{ij}(t) \right]{m \times n} = \begin{bmatrix} a'{11}(t) & a'{12}(t) & \cdots & a'{1n}(t) \\ a'{21}(t) & a'{22}(t) & \cdots & a'{2n}(t) \\ \vdots & \vdots & & \vdots \\ a'{m1}(t) & a'{m2}(t) & \cdots & a'_{mn}(t) \end{bmatrix}. dtdA(t)=[aij′(t)]m×n= a11′(t)a21′(t)⋮am1′(t)a12′(t)a22′(t)⋮am2′(t)⋯⋯⋯a1n′(t)a2n′(t)⋮amn′(t) .
对 A ( t ) A(t) A(t) 求导,就是对 A ( t ) A(t) A(t) 的每个元素求导。
任何数字矩阵的导数均为零矩阵
3、 单元函数矩阵求导运算的性质
- 线性性: d d t [ α A ( t ) + β B ( t ) ] = α d A ( t ) d t + β d B ( t ) d t ; \frac{\mathrm{d}}{\mathrm{d}t} \left[ \alpha A(t) + \beta B(t) \right] = \alpha \frac{\mathrm{d}A(t)}{\mathrm{d}t} + \beta \frac{\mathrm{d}B(t)}{\mathrm{d}t}; dtd[αA(t)+βB(t)]=αdtdA(t)+βdtdB(t);
- 乘积的导数(顺序不能交换): d d t [ A ( t ) B ( t ) ] = d A ( t ) d t B ( t ) + A ( t ) d B ( t ) d t ; \frac{\mathrm{d}}{\mathrm{d}t} \left[ A(t) B(t) \right] = \frac{\mathrm{d}A(t)}{\mathrm{d}t} B(t) + A(t) \frac{\mathrm{d}B(t)}{\mathrm{d}t}; dtd[A(t)B(t)]=dtdA(t)B(t)+A(t)dtdB(t);
- 复合函数的矩阵的导数: d d t A ( f ( t ) ) = d A ( u ) d u d f ( t ) d t ( u = f ( t ) ) ; \frac{\mathrm{d}}{\mathrm{d}t} A(f(t)) = \frac{\mathrm{d}A(u)}{\mathrm{d}u} \frac{\mathrm{d}f(t)}{\mathrm{d}t} \quad (u = f(t)); dtdA(f(t))=dudA(u)dtdf(t)(u=f(t));
- 逆矩阵的导数(只是用于推导,真正求出逆矩阵后就可以直接对他求导就好了): d A − 1 ( t ) d t = − A − 1 ( t ) d A ( t ) d t A − 1 ( t ) ; \frac{\mathrm{d}A^{-1}(t)}{\mathrm{d}t} = -A^{-1}(t) \frac{\mathrm{d}A(t)}{\mathrm{d}t} A^{-1}(t); dtdA−1(t)=−A−1(t)dtdA(t)A−1(t);
- 转置的导数: d A T ( t ) d t = ( d A ( t ) d t ) T . \frac{\mathrm{d}A^T(t)}{\mathrm{d}t} = \left( \frac{\mathrm{d}A(t)}{\mathrm{d}t} \right)^T. dtdAT(t)=(dtdA(t))T.
二、单元函数矩阵的积分
1、定义
设 A ( t ) = [ a i j ( t ) ] m × n ( t ∈ R ) A(t)=\begin{bmatrix}a_{ij}(t) \end{bmatrix}{m\times n}(t \in \mathbb{R}) A(t)=[aij(t)]m×n(t∈R),若 ∀ i = 1 , 2 , ⋯ , m , j = 1 , 2 , ⋯ , n , a i j ( t ) \forall i = 1,2,\cdots,m,j=1,2,\cdots,n,a{ij}(t) ∀i=1,2,⋯,m,j=1,2,⋯,n,aij(t) 在 [ a , b ] [a,b] [a,b] 上都可积,则称 A ( t ) A(t) A(t) 在 [ a . b ] [a.b] [a.b] 上可积,并且规定 A ( t ) A(t) A(t) 在 [ a , b ] [a,b] [a,b] 上的定积分为:
∫ a b A ( t ) d t = [ ∫ a b a i j ( t ) d t ] m × n ; \int_{a}^{b} A(t) \mathrm{d}t = \left[ \int_{a}^{b} a_{ij}(t) \mathrm{d}t \right]_{m \times n} ; ∫abA(t)dt=[∫abaij(t)dt]m×n;
类似地,不定积分为:
∫ a b A ( t ) d t = [ ∫ a b a i j ( t ) d t ] m × n . \int_{a}^{b} A(t) \mathrm{d}t = \left[ \int_{a}^{b} a_{ij}(t) \mathrm{d}t \right]_{m \times n} . ∫abA(t)dt=[∫abaij(t)dt]m×n.
简单地说,对 A ( t ) A(t) A(t) 求积分,就是对 A ( t ) A(t) A(t) 的每个元素求积分。
2、单元函数矩阵的积分元算的性质

3、单元向量值函数的微分与积分
单元向量值函数是单元函数矩阵的特殊情况,就是只有一行的单元函数矩阵。
f ( t ) = ( f 1 ( t ) , f 2 ( t ) , ⋯ , f m ( t ) ) T f(t)=\begin{pmatrix}f_1(t), f_2(t),\cdots,f_m(t)\end{pmatrix}^T f(t)=(f1(t),f2(t),⋯,fm(t))T
关于 t t t 求导数和积分,就是将其各个坐标函数关于 t t t 求导数和积分:
f ′ ( t ) = ( f 1 ′ ( t ) , f 2 ′ ( t ) , ⋯ , f m ′ ( t ) ) T , f'(t) = (f'1(t), f'2(t), \cdots, f'm(t))^T , f′(t)=(f1′(t),f2′(t),⋯,fm′(t))T,
∫ a b f ( t ) d t = ( ∫ a b f 1 ( t ) d t , ∫ a b f 2 ( t ) d t , ⋯ , ∫ a b f m ( t ) d t ) T . \int{a}^{b} f(t)\mathrm{d}t = \left( \int{a}^{b} f_1(t)\mathrm{d}t, \int{a}^{b} f_2(t)\mathrm{d}t, \cdots, \int_{a}^{b} f_m(t)\mathrm{d}t \right)^T . ∫abf(t)dt=(∫abf1(t)dt,∫abf2(t)dt,⋯,∫abfm(t)dt)T.
三、多元向量值函数的导数
1、n元m维向量值函数
n元m维向量值函数中, n n n 元就是值输入的是一组包含 n n n 个变量的向量
x = ( x 1 , x 2 , ⋯ , x n ) x= (x_1,x_2,\cdots,x_n) x=(x1,x2,⋯,xn)
m维指的是输出向量也是 m m m 维空间
y = ( y 1 , y 2 , ⋯ , y m ) y=(y_1,y_2,\cdots,y_m) y=(y1,y2,⋯,ym)
f ( x ) = ( f 1 ( x ) f 2 ( x ) ⋮ f m ( x ) ) f(x) = \begin{pmatrix} f_1(x) \\ f_2(x) \\ \vdots \\ f_m(x) \end{pmatrix} f(x)= f1(x)f2(x)⋮fm(x)

2、多元向量值函数的导数

d f d x ( x ) = f ′ ( x ) = [ ∂ f 1 ∂ x 1 ( x ) ∂ f 1 ∂ x 2 ( x ) ⋯ ∂ f 1 ∂ x n ( x ) ∂ f 2 ∂ x 1 ( x ) ∂ f 2 ∂ x 2 ( x ) ⋯ ∂ f 2 ∂ x n ( x ) ⋮ ⋮ ⋮ ∂ f m ∂ x 1 ( x ) ∂ f m ∂ x 2 ( x ) ⋯ ∂ f m ∂ x n ( x ) ] . \frac{\mathrm{d}f}{\mathrm{d}x}(x) = f'(x) = \begin{bmatrix} \frac{\partial f_1}{\partial x_1}(x) & \frac{\partial f_1}{\partial x_2}(x) & \cdots & \frac{\partial f_1}{\partial x_n}(x) \\ \frac{\partial f_2}{\partial x_1}(x) & \frac{\partial f_2}{\partial x_2}(x) & \cdots & \frac{\partial f_2}{\partial x_n}(x) \\ \vdots & \vdots & & \vdots \\ \frac{\partial f_m}{\partial x_1}(x) & \frac{\partial f_m}{\partial x_2}(x) & \cdots & \frac{\partial f_m}{\partial x_n}(x) \end{bmatrix} . dxdf(x)=f′(x)= ∂x1∂f1(x)∂x1∂f2(x)⋮∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)⋮∂x2∂fm(x)⋯⋯⋯∂xn∂f1(x)∂xn∂f2(x)⋮∂xn∂fm(x) .
通常称上面 m × n m \times n m×n 矩阵为 f ( x ) f(x) f(x) 在点 x x x 处的雅各比 (Jacobi) 矩阵
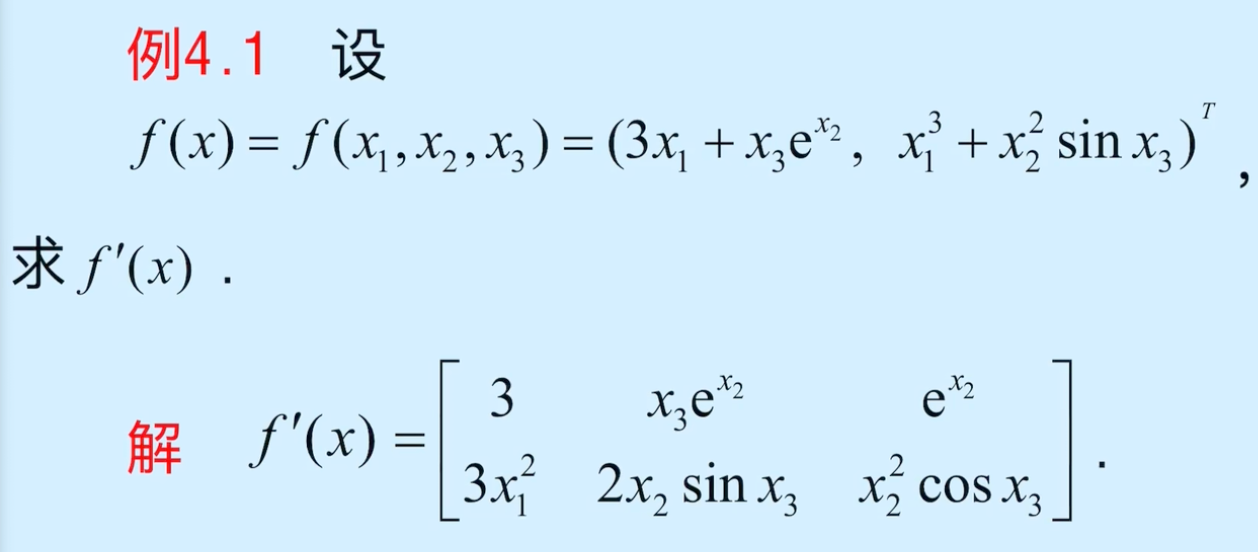
3、多元数值函数的导数与二阶导数
当 m = 1 m=1 m=1 时, f ( x ) = f ( x − 1 , x 2 , ⋯ , x n ) f(x)=f(x-1,x_2,\cdots,x_n) f(x)=f(x−1,x2,⋯,xn) 就是通常的 n n n 元值函数
它在点 x = ( x 1 , x 2 , ⋯ , x n ) T x=(x_1,x_2,\cdots,x_n)^T x=(x1,x2,⋯,xn)T 处的导数为 n n n 维向量
f ′ ( x ) = ( ∂ f ∂ x 1 ( x ) , ∂ f ∂ x 2 ( x ) , ⋯ , ∂ f ∂ x n ( x ) ) . f'(x) = \left( \frac{\partial f}{\partial x_1}(x), \frac{\partial f}{\partial x_2}(x), \cdots, \frac{\partial f}{\partial x_n}(x) \right). f′(x)=(∂x1∂f(x),∂x2∂f(x),⋯,∂xn∂f(x)).
这就是 f ( x ) = f ( x 1 , x 2 , ⋯ , x n ) f(x) = f(x_1,x_2,\cdots,x_n) f(x)=f(x1,x2,⋯,xn) 在点 x = ( x 1 , x 2 , ⋯ , x n ) T x=(x_1,x_2,\cdots,x_n)^T x=(x1,x2,⋯,xn)T 处的梯度向量。
如果 n n n 元 n n n 维向量值函数
f ′ ( x ) = ( ∂ f ∂ x 1 ( x ) , ∂ f ∂ x 2 ( x ) , ⋯ , ∂ f ∂ x n ( x ) ) . f'(x) = \left( \frac{\partial f}{\partial x_1}(x), \frac{\partial f}{\partial x_2}(x), \cdots, \frac{\partial f}{\partial x_n}(x) \right). f′(x)=(∂x1∂f(x),∂x2∂f(x),⋯,∂xn∂f(x)).
在 x 0 ∈ Ω x_0 \in \Omega x0∈Ω 处可导,则称 f ′ ′ ( x 0 ) f^{''}(x_0) f′′(x0) 为 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处的二阶导数。
f ′ ′ ( x 0 ) = d f ′ d x ( x 0 ) = [ f x 1 x 1 ′ ′ ( x 0 ) f x 1 x 2 ′ ′ ( x 0 ) ⋯ f x 1 x n ′ ′ ( x 0 ) f x 2 x 1 ′ ′ ( x 0 ) f x 2 x 2 ′ ′ ( x 0 ) ⋯ f x 2 x n ′ ′ ( x 0 ) ⋮ ⋮ ⋮ f x n x 1 ′ ′ ( x 0 ) f x n x 2 ′ ′ ( x 0 ) ⋯ f x n x n ′ ′ ( x 0 ) ] 记为 = H f''(x_0) = \frac{\mathrm{d}f'}{\mathrm{d}x}(x_0) = \begin{bmatrix} f''{x_1 x_1}(x_0) & f''{x_1 x_2}(x_0) & \cdots & f''{x_1 x_n}(x_0) \\ f''{x_2 x_1}(x_0) & f''{x_2 x_2}(x_0) & \cdots & f''{x_2 x_n}(x_0) \\ \vdots & \vdots & & \vdots \\ f''{x_n x_1}(x_0) & f''{x_n x_2}(x_0) & \cdots & f''_{x_n x_n}(x_0) \end{bmatrix} \text{记为} = H f′′(x0)=dxdf′(x0)= fx1x1′′(x0)fx2x1′′(x0)⋮fxnx1′′(x0)fx1x2′′(x0)fx2x2′′(x0)⋮fxnx2′′(x0)⋯⋯⋯fx1xn′′(x0)fx2xn′′(x0)⋮fxnxn′′(x0) 记为=H
上面的n阶方阵 H H H 通常称为 n n n 元数值函数 f f f 在 x 0 ∈ Ω x_0 \in \Omega x0∈Ω 处的黑塞(Hesse)矩阵。当各个二阶偏导数连续时,黑塞矩阵时对称矩阵。