📢本篇文章是博主强化学习(RL)领域学习时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在👉强化学习专栏:
【启发式算法】(12)---《狼群算法(Wolf Pack Algorithm, WPA)算法详细介绍》
狼群算法(Wolf Pack Algorithm, WPA)算法详细介绍
目录
[4.1 符号体系](#4.1 符号体系)
[4.2 三大智能行为](#4.2 三大智能行为)
[4.3 强者生存机制(Population Renewal)](#4.3 强者生存机制(Population Renewal))
[[Python] WPA算法实现](#[Python] WPA算法实现)
[[Notice] 注意事项](#[Notice] 注意事项)
1.算法绪论
随着仿真、金融、能源、航天等领域对优化模型精度要求的不断提高,决策变量维度迅速膨胀,传统梯度类方法面临"维数灾难"与"局部陷阱"双重瓶颈。近二十年来,群体智能(Swarm Intelligence)以无梯度、高并行、鲁棒性强等优势异军突起,其中粒子群(PSO)、蚁群(ACO)、人工鱼群(AFSA)等算法已被广泛引用,但在 100 维以上的多峰问题中仍易出现早熟收敛。
2013 年,吴虎胜等受狼群捕食行为启发,在《系统工程与电子技术》提出狼群算法(Wolf Pack Algorithm, WPA)。该算法通过抽象"游走---召唤---围攻"三层协作机制,并引入"胜者为王"的头狼更新规则与"强者生存"的种群淘汰策略,在 15 座国际通用测试函数、最高 200 维场景下取得显著优于 PSO、AFSA、GA 的综合表现,为高维复杂优化提供了新的可行范式。
2.算法理解
想象你是一只狼。
冬天到了,雪原上食物稀缺,你和同伴必须合作找到那只肥美的鹿。你们不会一拥而上,而是分工明确:
-
几只"探狼"先出去闻味道,谁闻到最浓的血腥味,谁就"嗷呜"一声。
-
头狼收到信号,立刻"嚎叫"召集"猛狼"狂奔过来。
-
大家围成一圈,步步逼近,最终一起把鹿放倒。
-
分肉时,谁功劳大谁先吃,弱狼可能饿肚子------但整个族群越来越强。
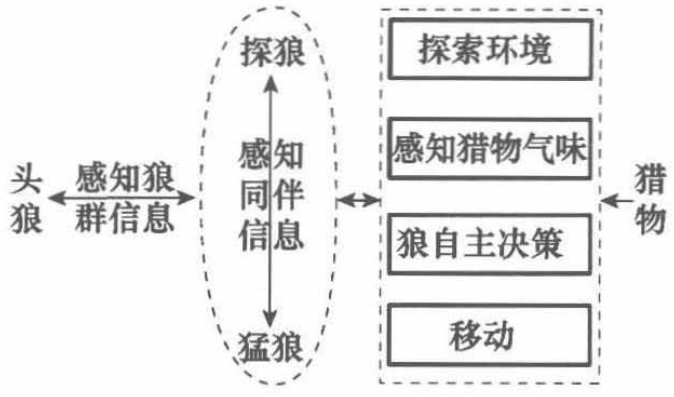
把这套"狼群战术"写成数学,就是 2013 年吴虎胜等人在《系统工程与电子技术》提出的 狼群算法(Wolf Pack Algorithm, WPA)。
3.算法流程
WPA算法分简单可以分5 步走
初始化 → 探狼游走 → 猛狼奔袭 → 合围攻击 → 强者生存(淘汰弱狼)

| 生物角色 | 对应解空间里的"个体" | 数学意义 | 功能描述 |
|---|---|---|---|
| 头狼 | 当前最优解 | 全局最优候选 | 保存当前最佳决策向量,引导群体搜索方向 |
| 探狼 | 除头狼外最好的 S_num 匹狼 | 局部搜索,防止漏掉好解 | 在解空间边缘执行精细探测,负责"广域勘探" |
| 猛狼 | 被头狼召唤的其余狼 | 快速向优解区域聚集 | 响应头狼召唤,执行"区域开采" |
| 猎物分配 | 目标函数 f(x) | 越"香"→函数值越大(假设求 max) | 按贡献度优先分配资源,弱狼被淘汰以维持种群多样性 |

4.数学模型
4.1 符号体系
-
搜索空间 Ω ⊂ ℝᴰ,第 i 匹狼状态 xᵢ = (xᵢ¹,...,xᵢᴰ)
-
目标函数(最大化)(x)→ ℝ,称为"气味浓度"
-
种群规模 N,最大迭代 k_max
-
步长因子 S、距离判定因子 ω、更新比例因子 β
4.2 三大智能行为
-
游走行为(Scouting)
探狼集合大小 S_num ∈ [N/(α+1), N/α]。每匹探狼在 h 个方向试探:
xᵢᵈᵖ = xᵢᵈ + sin(2πp/h) · step_r , p=1,...,h若任一方向气味浓度高于头狼,则立即替换头狼并转入召唤阶段;否则继续游走直至达到最大游走次数 T_max。
-
召唤行为(Summoning)
头狼通过"嚎叫"广播位置 g;猛狼以较大步长 step_b 奔袭:
xᵢ(k+1) = xᵢ(k) + step_b · (g(k) − xᵢ(k)) / ‖g(k) − xᵢ(k)‖₂奔袭途中若发现更优解,即行"夺权"。当与头狼距离小于阈值 d_near 时转入围攻。
阈值估算:
d_near = (1/Dω) · Σ_{d=1}^{D}(max_d − min_d) -
围攻行为(Beleaguering)
将头狼位置视为猎物质心,实施多向压缩:
xᵢ(k+1) = xᵢ(k) + λ · step_c · (g(k) − xᵢ(k))λ∼U(−1,1) 保证各向同性搜索。若新位置气味提升则接受,否则保持原状态。
4.3 强者生存机制(Population Renewal)
每代淘汰适应度最差的 R = uniform[N/(2β), N/β] 匹狼,并随机生成等量新个体,以维持多样性并防止早熟。
5.收敛性分析
引理 1 WPA 种群序列 {Q_k} 为有限齐次马尔可夫链。
引理 2 该链不可约、非周期且正常返,故为遍历链。
引理 3 若进化算法满足"任意状态可达"且"种群单调不劣化",则以概率 1 收敛至全局最优。
定理 WPA 满足上述两条件,因此具有概率 1 全局收敛性。
论文用马尔可夫链 证明:
狼群状态序列是"有限、齐次、遍历"的,而且单调不劣化 ,所以 WPA 以概率 1 收敛到全局最优。
(非数学专业读者可直接记结论:它理论上不会"集体犯傻"。)
6.实验亮点
实验测试集设计:
覆盖 2--200 维、单峰/多峰、可分/不可分共 15 个经典函数,例如 Sphere、Rastrigin、Ackley、Quadric 等。
对比算法与评价指标:
-
PSO(标准版)、AFSA、GA( Sheffield 工具箱)
-
指标:最优值、最差值、均值、标准差、成功率(|f*−f_opt|/|f_opt|<1e−3)、平均耗时
-
独立运行 100 次,种群规模统一 50,最大迭代 2000
| 函数特色 | 例子 | 维度 | PSO | GA | FSA | WPA |
|---|---|---|---|---|---|---|
| 低维单峰 | Matyas | 2 | ✅ | ✅ | ✅ | ✅ |
| 30 维单峰 | Sphere | 30 | 偶尔失效 | 失效 | 失效 | 100% 成功率 |
| 200 维多峰 | Ackley | 200 | 误差 2.0+ | 误差 18+ | 误差 20+ | 误差 ≈ 0 |
| 耗时 | 中等 | 慢 | 最慢 | 比 PSO 还快一丢丢 |
结论:
维数越高、峰越多,WPA 越香!
-
单次迭代时间复杂度 O(N·D·h),其中 h 为探狼试探方向数。
-
实验平台:Windows XP、2 GB 内存、MATLAB R2008a。
-
在 30 维 Sphere 函数上,WPA 平均耗时 0.75 s,低于 GA(26.7 s)与 AFSA(67.0 s),与 PSO(2.54 s)相比亦有优势
[Python] WPA算法实现
python
"""《WPA算法》
时间:2024.10.29
作者:不去幼儿园
"""
import numpy as np
def WPA(f, N=50, D=10, k_max=500, alpha=4, beta=6, S=1000, w=500):
# 1. 初始化
X = np.random.uniform(low, high, (N, D))
Y = np.array([f(x) for x in X])
g = X[np.argmax(Y)].copy() # 头狼
for k in range(k_max):
# 2. 探狼游走
S_num = np.random.randint(N//(alpha+1), N//alpha)
for i in np.argsort(-Y)[:S_num]:
for _ in range(T_max):
directions = random_directions()
x_try = X[i] + step_r * directions
y_try = f(x_try)
if y_try > Y[i]:
X[i], Y[i] = x_try, y_try
if y_try > f(g): g = x_try.copy()
break
# 3. 猛狼奔袭 + 4. 围攻
M_num = N - S_num - 1
for i in np.argsort(-Y)[S_num+1:]:
while distance(X[i], g) > d_near:
X[i] += step_b * (g - X[i]) / distance(X[i], g)
Y[i] = f(X[i])
if Y[i] > f(g): g = X[i].copy()
# 围攻
x_att = X[i] + step_c * (2*np.random.rand(D)-1)
if f(x_att) > Y[i]:
X[i], Y[i] = x_att, f(x_att)
# 5. 强者生存
R = np.random.randint(N//(2*beta), N//beta)
worst = np.argsort(Y)[:R]
X[worst] = np.random.uniform(low, high, (R, D))
Y[worst] = [f(x) for x in X[worst]]
return g, f(g)7.超参数(实战经验)
-
距离判定因子 ω
控制"奔袭→围攻"切换。实验表明 ω∈[200,1000] 时算法稳定;ω>1200 导致切换过迟,精细搜索不足,成功率下降。
-
步长因子 S
决定搜索粒度。S∈[200,1200] 可在收敛精度与迭代次数之间取得平衡;S>1400 步长过小,探索效率降低。
值得注意的是,α 与 β 在限定区间内随机取值即可,对性能不敏感,显著降低了调参难度。
| 参数 | 作用 | 推荐范围 | 过大后果 | 过小后果 |
|---|---|---|---|---|
| 距离判定因子 ω | 控制猛狼何时转围攻 | 200--1000 | 很难合围,迭代暴涨 | 合围太早,粗粗糙糙 |
| 步长因子 S | 控制精细程度 | 200--1200 | 步长太小,跑不动 | 步长大,漏最优 |
WPA 的隐藏优点:α、β 在区间内随机取即可,对最终成绩不敏感,手残党友好。
[Notice] 注意事项
什么时候用 WPA?
-
目标函数维数高(>50 维)。
-
landscape 崎岖,大量局部极值。
-
传统 PSO/GA 容易早熟,成功率低。
-
你愿意牺牲一点点代码复杂度,换取更高的成功率。
bash
# 环境配置
Python 3.11.5
torch 2.1.0
torchvision 0.16.0
gym 0.26.28.局限性
现存局限:
-
算子较多,工程实现相对复杂
-
理论分析目前仍局限于概率收敛,缺乏有限时间收敛速率估计
-
对于超高维(>1000 维)或动态优化问题,需进一步与分布式、并行计算框架结合
9.总结
狼群算法通过"游走---召唤---围攻"三层协作以及"胜者为王、强者生存"的演化机制,在全局勘探与局部开采之间实现了动态平衡。理论分析与大量实验共同表明,WPA 对高维、多峰复杂函数具有显著的求解精度、成功率和鲁棒性优势
狼群算法 ="探狼到处闻 + 猛狼听嚎冲 + 合围精细搜 + 弱狼被淘汰"。
把狼的生存智慧翻译成代码,就能在 200 维山峰里找到最低的那块洼地!
参考文献
1\] 吴虎胜, 张凤鸣, 吴庐山. 一种新的群体智能算法------狼群算法\[J\]. 系统工程与电子技术, 2013, 35(11): 2430-2438. \[2\] Kennedy J, Eberhart R. Particle swarm optimization\[C\]//IEEE International Conference on Neural Networks. 1995: 1942-1948. \[3\] Li X L, Shao Z J, Qian J X. An optimizing method based on autonomous animats: fish swarm algorithm\[J\]. 系统工程理论与实践, 2002, 22(11): 32-38. \[4\] Srinivas M, Patnaik L M. Genetic algorithms: a survey\[J\]. Computer, 1994, 27(6): 17-26. > 更多**启发式算法** 文章,请前往:[【启发式算法】专栏](https://blog.csdn.net/qq_51399582/category_12782813.html "【启发式算法】专栏") *** ** * ** *** > 博客都是给自己看的笔记,如有误导深表抱歉。文章若有不当和不正确之处,还望理解与指出。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请联系博主删除。如有错误、疑问和侵权,欢迎评论留言联系作者,或者添加VX:**Rainbook_2,**联系作者。✨