对于刚入门神经网络的同学来说，"感知机" 是绕不开的基础 ------ 它是最早的神经网络模型，也是后续复杂神经网络（如多层感知机、深度学习）的 "最小单元"。今天我们从感知机的核心定义出发，拆解其模型结构、数学原理、激活函数，再通过 "苹果香蕉分类""数值计算例题" 两个实战案例，帮你彻底搞懂 "感知机如何学习分类规律"，为后续深入学习神经网络打下坚实基础。
一、先明确：感知机是什么？为什么重要？
在学习细节前，我们先建立对感知机的基本认知 ------ 它不是复杂模型，而是 "模拟人类神经元判断逻辑的简单数学工具"，是理解神经网络的关键起点。
1. 感知机的定义：早期的神经网络模型
感知机由美国学者 F.Rosenblatt 于 1957 年提出，是首个具有 "学习能力" 的神经网络模型。它的核心思想是：通过 "监督学习"（利用带标签的训练数据）调整参数，逐步提升对数据模式的分类能力 ------ 简单来说，感知机能 "从数据中学习如何区分不同类别"，而不是依赖人工预设的规则。
比如要区分 "苹果" 和 "香蕉"，我们不需要手动编写 "红色圆形是苹果、黄色弯形是香蕉" 的规则，只需给感知机输入带标签的样本（苹果→标签 1，香蕉→标签 0），它就能自动学习 "颜色""形状" 这两个特征的重要性，最终实现分类。
2. 感知机的地位：神经网络的 "基石"
感知机的价值不仅在于它能解决简单分类问题，更在于它奠定了后续复杂神经网络的基础：
- 后续的 "多层感知机"（MLP）就是将多个感知机按 "层" 排列，解决感知机无法处理的 "非线性问题"；
- 深度学习中的卷积神经网络（CNN）、循环神经网络（RNN），其基本单元的设计思路仍延续了感知机 "输入→加权求和→激活输出" 的逻辑。
可以说，理解感知机，就掌握了神经网络的 "最小运行单元"，后续学习复杂模型会更轻松。
二、感知机的模型结构：4 个核心组件与 "输入→输出" 流程
感知机的结构非常直观，本质是 "模拟生物神经元的信号处理逻辑"，由 4 个核心组件构成，完整流程可概括为 "输入→加权求和→激活→输出"。
1. 4 个核心组件（对应生物神经元功能）
感知机的每个组件都有明确的功能，对应生物神经元的 "树突→突触→细胞体→轴突"：
- 输入（Input） ：用
x₁, x₂, ..., xₙ表示，对应生物神经元的 "树突"，负责接收外部信号（如区分苹果香蕉时的 "颜色""形状" 特征）。每个输入都代表一个 "特征"，比如x₁是颜色，x₂是形状。 - 权重（Weight） ：用
w₁, w₂, ..., wₙ表示，对应生物神经元的 "突触"，代表 "每个输入特征的重要程度"。权重越大，该特征对最终输出的影响越强；权重为正表示 "该特征促进分类结果"（如 "红色" 对 "苹果" 分类是正向贡献），为负表示 "抑制分类结果"（如 "黄色" 对 "苹果" 分类是负向贡献）。 - 偏置（Bias） ：用
b表示，也叫 "偏移量"，是感知机的 "全局调整项"。它的作用是 "调整加权求和的基准"------ 比如即使所有输入特征的加权和为 0，偏置也能决定输出是 "激活" 还是 "抑制"，避免模型过度依赖输入特征。 - 激活函数（Activation Function） ：用
a(·)表示，对应生物神经元的 "细胞体"，负责将 "加权求和结果" 转换为 "最终输出"。它的核心作用是 "引入非线性"（或 "阈值判断"），决定感知机是否 "激活"------ 比如当加权求和结果超过某个阈值时，输出 1（激活），否则输出 0（抑制）。
2. "输入→输出" 的完整流程（数学表达）
感知机的信号处理流程可拆解为两步数学运算，最终得到输出结果y：
步骤 1：加权求和（组合函数）
首先计算 "输入特征 × 对应权重" 的总和，再加上偏置b，得到 "净输入"v（也叫 "线性组合结果"），公式为：v = w₁x₁ + w₂x₂ + ... + wₙxₙ + b或用向量表示（更简洁）：v = w·x + b（其中w是权重向量，x是输入向量，w·x表示两者的点积）。
这一步对应生物神经元 "整合树突接收的多个信号" 的过程，v就是整合后的 "总信号强度"。
步骤 2：激活函数（阈值判断）
将净输入v代入 "激活函数"a(·)，得到感知机的最终输出y，公式为：y = a(v)。
激活函数的作用是 "将连续的净输入v转换为离散的输出"（比如 0 或 1），实现 "分类判断"。常见的激活函数有 "阶跃函数""ReLU 函数" 等，后续会详细讲解。
3. 直观案例：用符号理解感知机流程
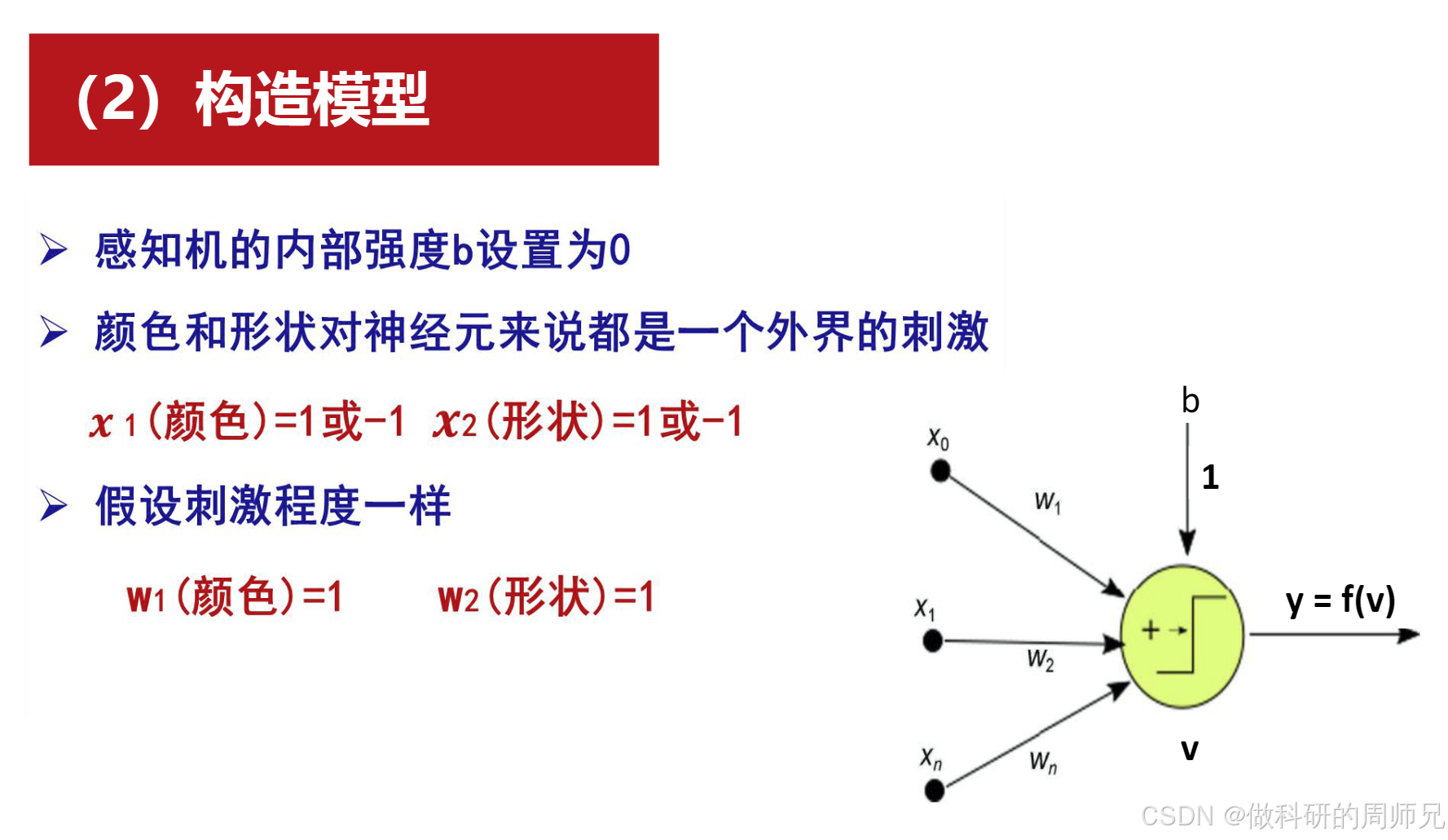
以 "苹果香蕉分类" 为例，假设输入特征是 "颜色（x₁）" 和 "形状（x₂）"，权重w₁=1（颜色重要）、w₂=1（形状重要），偏置b=0，激活函数是 "阶跃函数"（v≥0输出 1，v<0输出 0）：
- 若输入是苹果（x₁=1，x₂=1）：加权求和
v = 1×1 + 1×1 + 0 = 2，激活函数输出y=a(2)=1（判断为苹果）； - 若输入是香蕉（x₁=-1，x₂=-1）：加权求和
v = 1×(-1) + 1×(-1) + 0 = -2，激活函数输出y=a(-2)=0（判断为香蕉）。
整个流程完全模拟了 "根据特征判断类别" 的逻辑，且参数（w、b）可通过学习调整，非常灵活。
图片来源于网络，仅供学习参考
三、感知机的核心：激活函数的作用与常见类型
激活函数是感知机的 "决策核心"------ 没有激活函数，感知机的输出就是 "线性组合结果v"，只能处理 "线性可分" 问题；有了激活函数，感知机才能实现 "阈值判断"，完成分类任务。
1. 激活函数的核心作用
激活函数主要有两个作用，缺一不可：
- 阈值判断 ：将连续的净输入
v（可能是任意实数）转换为离散的输出（如 0 或 1），对应生物神经元 "达到阈值则激活，否则不激活" 的逻辑； - 引入非线性：虽然单个感知机的激活函数可能是 "分段线性" 的（如阶跃函数），但多个感知机组合时，激活函数能让整体模型处理 "非线性问题"（如用曲线区分两类样本）。
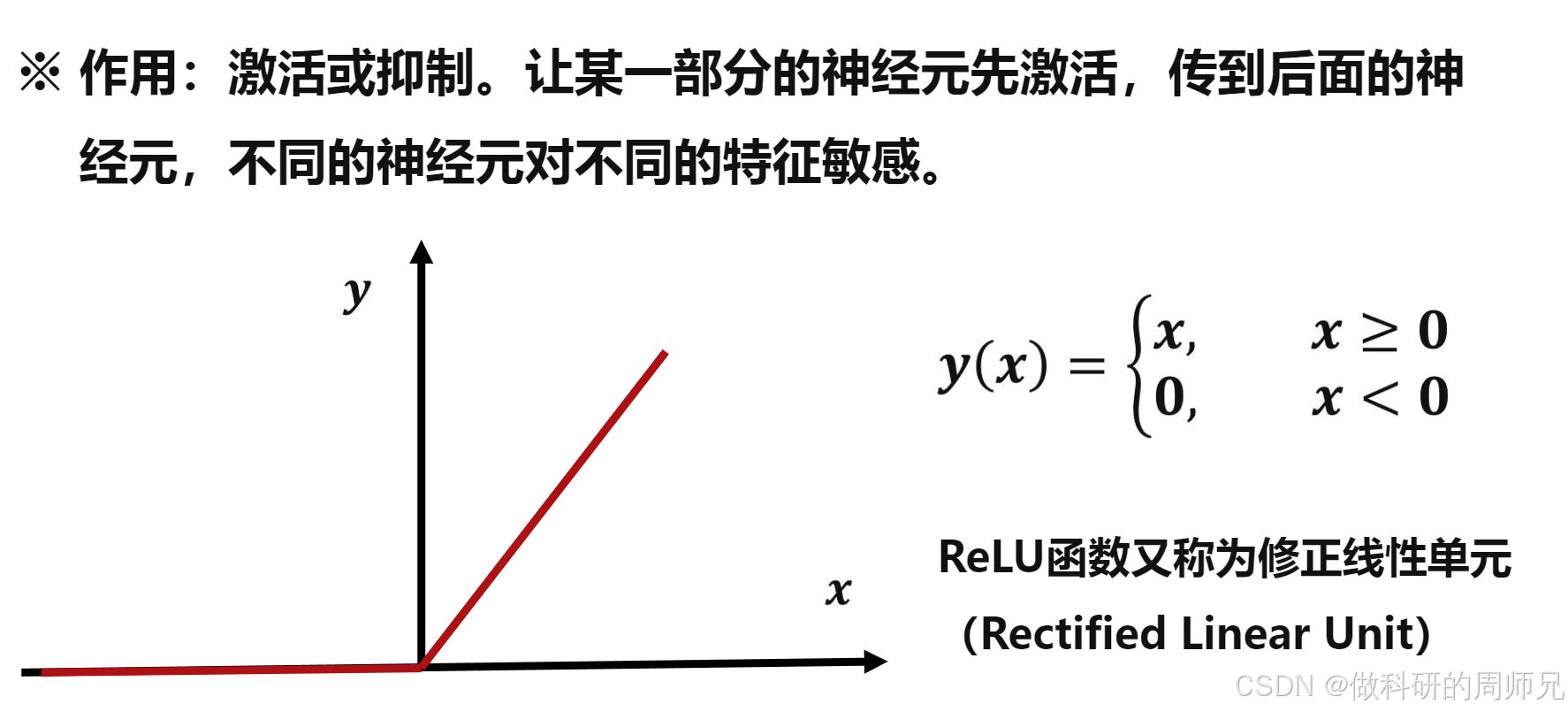图片来源于网络，仅供学习参考
3. 例题实战：用 ReLU 函数计算感知机输出
通过一道具体例题，掌握感知机的计算过程，理解每个参数的作用：
例题条件：
- 感知机参数：权重
w=(1.0, -0.75, 0.25)（3 个权重，对应 3 个输入特征），偏置b=-1； - 输入特征：
x=(-0.8, 0.2, -0.4)（3 个输入，与权重一一对应）； - 组合函数：sum 函数（即加权求和）；
- 激活函数：ReLU 函数。
图片来源于网络，仅供学习参考
计算步骤：
-
计算净输入
v（加权求和 + 偏置） ：v = w₁x₁ + w₂x₂ + w₃x₃ + b代入数值：v = (1.0×-0.8) + (-0.75×0.2) + (0.25×-0.4) + (-1)分步计算：= -0.8 - 0.15 - 0.1 - 1 = -2.05。 -
代入 ReLU 函数计算输出
y：因v=-2.05 < 0，根据 ReLU 函数定义，y=0。
图片来源于网络，仅供学习参考
结果分析：
该感知机最终输出 0，说明输入特征的 "总信号强度" 未达到激活阈值（ReLU 函数的阈值是 0），因此处于 "抑制" 状态。若想让输出变为正数值，可调整参数（如增大权重w₁，或减小偏置b的绝对值）。
四、感知机的学习过程：如何通过数据调整参数？
感知机的核心优势是 "能通过监督学习调整参数（w 和 b）"，而不是依赖人工预设 ------ 这就是它 "学习能力" 的来源。学习的目标是 "让感知机的预测输出y尽可能接近真实标签y_true"。
1. 学习的核心逻辑：误差驱动的参数更新
感知机的学习过程可概括为 "预测→计算误差→调整参数→重复"，核心是 "根据预测误差调整权重和偏置"，具体逻辑如下：
- 初始化参数 ：随机初始化权重
w（如小的随机数）和偏置b（通常初始化为 0）； - 输入训练样本 ：每次输入一个带标签的训练样本（
x，y_true），其中y_true是真实类别（如 1 = 苹果，0 = 香蕉）； - 前向计算预测输出 ：根据当前参数计算净输入
v和预测输出y（y=a(v)）； - 计算误差 ：误差
e = y_true - y（真实标签与预测输出的差值），e越大，说明当前参数越差； - 调整参数 ：根据误差
e和学习率η（控制每次参数调整的幅度，通常取 0.01~0.1），更新权重w和偏置b，更新公式为：- 权重更新：
w_i = w_i + η × e × x_i（对每个权重w_i）； - 偏置更新：
b = b + η × e；
- 权重更新：
- 迭代优化：重复步骤 2~5，直到所有训练样本的预测误差小于预设阈值，或迭代次数达到上限 ------ 此时感知机的参数已优化完成，能准确预测新样本。
2. 参数更新公式的直观理解
为什么这样的更新公式能减少误差？我们用 "苹果香蕉分类" 的案例解释：
- 假设某样本是苹果（
y_true=1），但感知机预测为 0（y=0），误差e=1-0=1； - 若输入特征
x₁=1（颜色为红色，对苹果是正向特征），则权重更新为w₁ = w₁ + η×1×1------w₁增大，下次遇到红色特征时，净输入v会更大，更易激活输出 1（正确预测）； - 偏置更新为
b = b + η×1------b增大，也会提升净输入v，帮助正确激活。
反之，若样本是香蕉（y_true=0），预测为 1（y=1），误差e=-1，则权重和偏置会相应减小，避免下次误判。
五、感知机的实战案例：区分苹果和香蕉
通过 "苹果香蕉分类" 的完整案例，将感知机的模型结构、激活函数、学习过程串联起来，直观感受感知机如何解决实际分类问题。
图片来源于网络，仅供学习参考
1. 步骤 1：定义问题与特征标签
首先明确分类任务的 "特征" 和 "标签"，将现实问题转化为数学数据：
- 分类目标：区分苹果（正类）和香蕉（负类）；
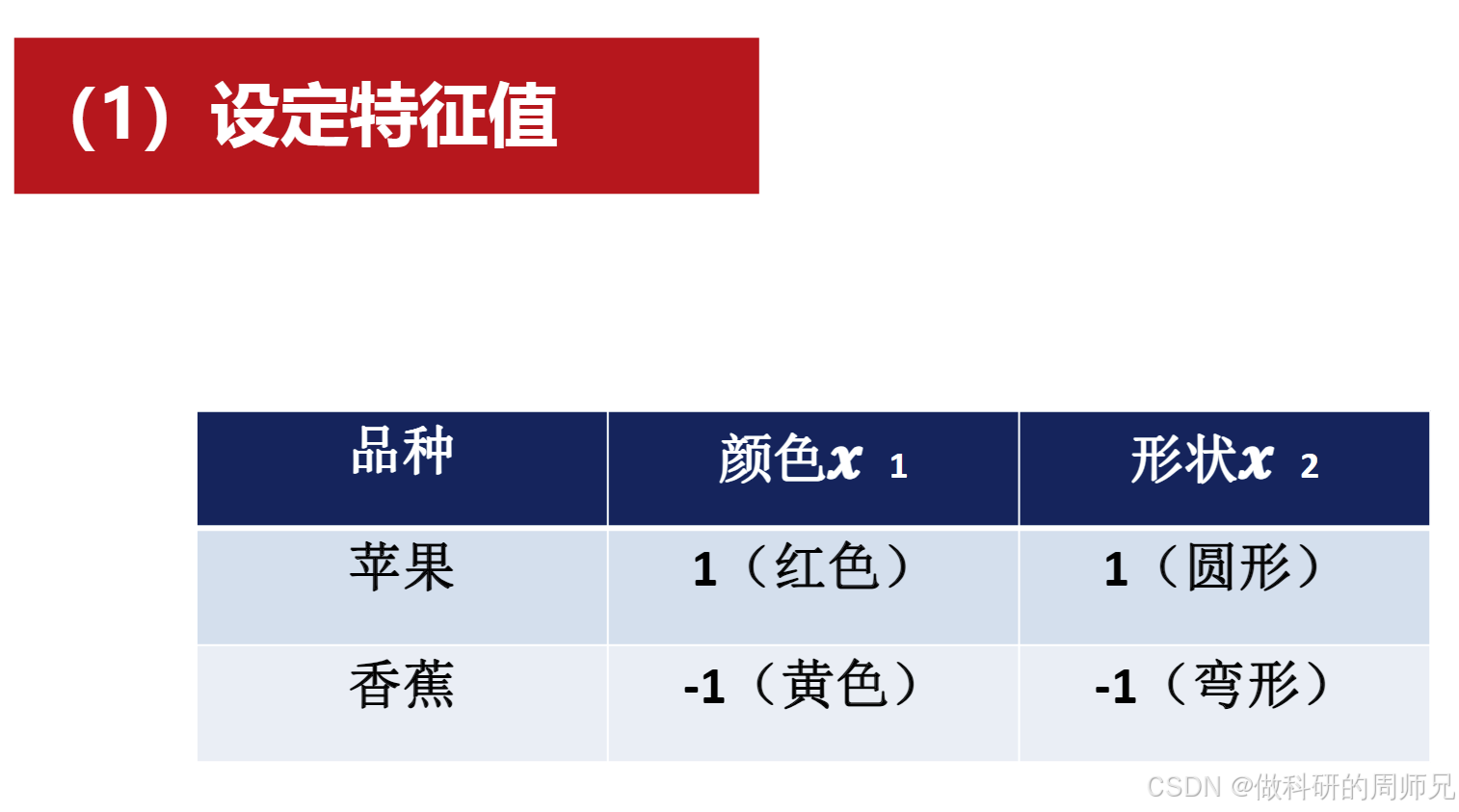
- 特征选择 ：选择 "颜色（x₁）" 和 "形状（x₂）" 两个关键特征，并用数值表示：
- 颜色：红色（苹果）=1，黄色（香蕉）=-1；
- 形状：圆形（苹果）=1，弯形（香蕉）=-1；
- 标签：苹果 = 1，香蕉 = 0；
- 训练样本 ：共 2 个样本，分别是：
- 苹果：
(x₁=1, x₂=1)，y_true=1； - 香蕉：
(x₁=-1, x₂=-1)，y_true=0。
- 苹果：
图片来源于网络，仅供学习参考
2. 步骤 2：初始化感知机参数
- 权重：因 "颜色" 和 "形状" 对分类的重要性相同，初始化为
w₁=1，w₂=1； - 偏置：初始化为
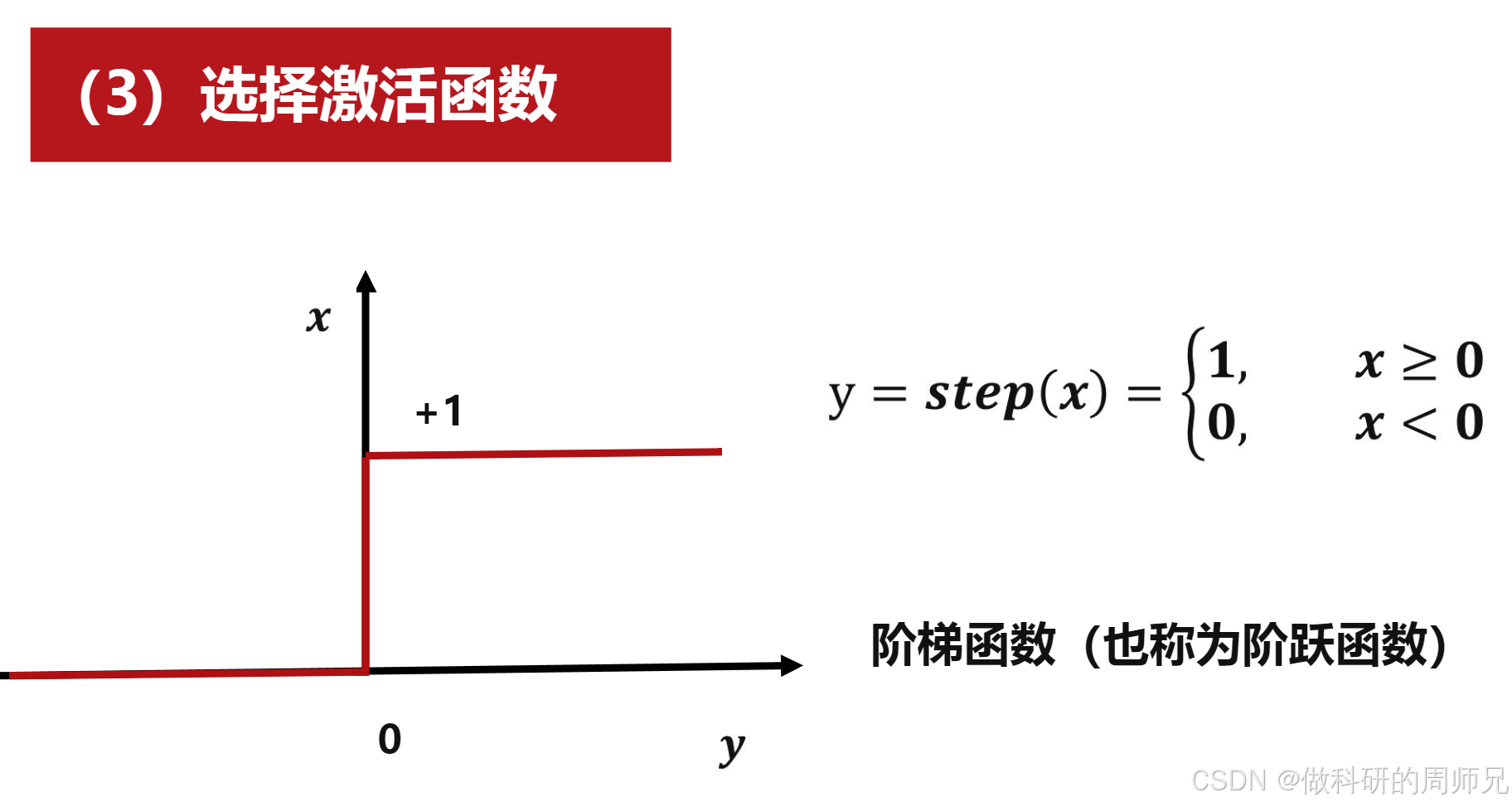
b=0； - 激活函数：选择阶跃函数（
v≥0输出 1，v<0输出 0），适合二分类； - 学习率：
η=0.1（较小的学习率，保证参数稳定更新）。
图片来源于网络，仅供学习参考
图片来源于网络，仅供学习参考
3. 步骤 3：第一次迭代（输入苹果样本）
- 输入样本 ：
x=(1,1)，y_true=1； - 计算净输入
v：v = 1×1 + 1×1 + 0 = 2； - 激活输出
y：因v=2≥0，阶跃函数输出y=1； - 计算误差 ：
e = 1 - 1 = 0（预测正确，无需调整参数）。
图片来源于网络，仅供学习参考
4. 步骤 4：第二次迭代（输入香蕉样本）
- 输入样本 ：
x=(-1,-1)，y_true=0； - 计算净输入
v：v = 1×(-1) + 1×(-1) + 0 = -2； - 激活输出
y：因v=-2<0，阶跃函数输出y=0； - 计算误差 ：
e = 0 - 0 = 0（预测正确，无需调整参数）。
5. 结果：感知机成功区分苹果和香蕉
经过 2 次迭代，感知机对两个训练样本的预测均正确，误差为 0，参数（w₁=1，w₂=1，b=0）已满足分类需求：
- 对任意苹果样本（
x₁=1，x₂=1），v=2≥0，输出 1（正确）； - 对任意香蕉样本（
x₁=-1，x₂=-1），v=-2<0，输出 0（正确）。
图片来源于网络，仅供学习参考
6. 关键思考：参数修改会影响分类结果吗？
若将权重改为w₁=2，w₂=1，偏置b=1，重新计算香蕉样本的输出：
- 净输入
v = 2×(-1) + 1×(-1) + 1 = -2 -1 +1 = -2； - 激活输出
y=0（正确），仍能区分香蕉。
若将偏置改为b=3，计算香蕉样本的输出：
- 净输入
v = 1×(-1) + 1×(-1) + 3 = 1； - 激活输出
y=1（错误，将香蕉判为苹果）------ 这说明参数设置不当会导致分类错误，需通过学习调整。
六、感知机的局限性与改进方向
感知机虽然是神经网络的基础，但也有明显的局限性 ------ 这也是后续多层感知机、深度学习出现的原因。
1. 核心局限性：无法处理 "非线性可分" 问题
感知机的最大局限是 "只能处理线性可分的数据"------ 即数据能通过一条直线（2 维）、一个平面（3 维）或一个超平面（高维）完全区分。若数据是 "非线性可分" 的（如用曲线才能区分），感知机永远无法收敛（误差无法降到 0）。
最经典的例子是 "异或（XOR）问题"：
- 异或的输入输出关系是：(0,0)→0，(0,1)→1，(1,0)→1，(1,1)→0；
- 无论如何调整感知机的参数（w 和 b），都无法用一条直线将 "输出 1" 和 "输出 0" 的样本完全分开 ------ 感知机对异或问题无解。
2. 改进方向：从 "单个感知机" 到 "多层感知机"
解决感知机局限性的核心思路是 "增加感知机的层数"，构建 "多层感知机（MLP）"：
- 多层感知机包含 "输入层→隐藏层→输出层"，其中 "隐藏层" 由多个感知机构成；
- 隐藏层的引入让模型能处理 "非线性问题"------ 因为多个 "线性组合 + 激活" 的叠加，整体会形成非线性映射，能拟合曲线形状的决策边界；
- 比如异或问题，用 "输入层（2 个神经元）→隐藏层（2 个神经元）→输出层（1 个神经元）" 的多层感知机，就能轻松解决。
七、入门总结与学习建议
- 核心逻辑回顾：感知机是 "输入→加权求和→激活输出" 的简单模型，通过监督学习调整权重和偏置，实现对线性可分数据的分类，是神经网络的基础单元。
- 关键概念记忆 ：
- 模型结构：输入（特征）、权重（重要性）、偏置（基准调整）、激活函数（阈值判断）；
- 学习过程：误差驱动的参数更新（
w_i = w_i + η×e×x_i，b = b + η×e）； - 局限性：只能处理线性可分问题，无法解决异或等非线性问题。
- 学习建议 ：
- 动手计算：像 "ReLU 函数例题""苹果香蕉分类" 这样的案例，手动代入数值计算，感受参数对输出的影响；
- 代码实践：用 Python 手动实现感知机（后续会提供模板），训练简单的线性可分数据集（如鸢尾花分类的子集），直观观察参数更新过程；
- 关联后续知识：理解感知机的局限性后，再学习多层感知机，就能明白 "隐藏层" 的价值，形成完整的知识链。
对于刚入门的同学，不需要一开始深入感知机的数学证明（如收敛性定理），重点是理解 "模型结构""计算流程" 和 "参数更新逻辑"。后续我们会通过代码实践，带你亲手实现感知机，体验它如何从 "随机参数" 逐步学习到 "正确分类"，进一步加深理解。