moveit使用和机器人模型与状态--正向运动学和逆向运动学分析（四）

经过以上的学习，相信可以对基本的机器人的规划和控制有了一个初级的认识了，接下来我们需要认识一下更多关于机器人模型的事情。

机器人模型和机器人状态

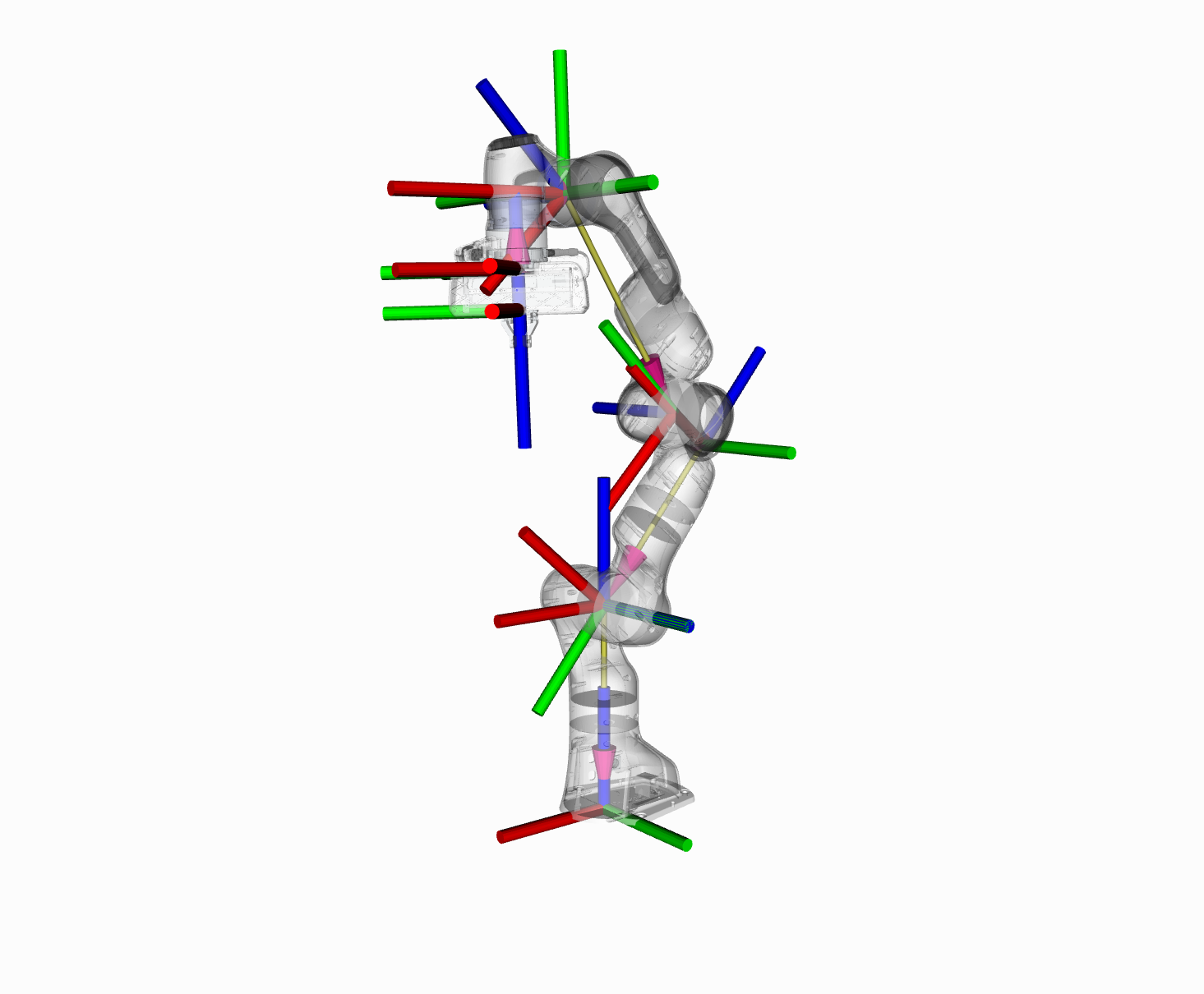
在本节中，我们将引导您了解在 MoveIt 中使用运动学的 C++ API。

RobotModel 和 RobotState 类

RobotModel 和 RobotState 类是核心类，可让您访问机器人的运动学。

RobotModel 类包含所有链接和关节之间的关系，包括从 URDF 加载的关节极限属性。RobotModel 还将机器人的链节和关节划分为 SRDF 中定义的规划组。有关 URDF 和 SRDF 的单独教程可在此处找到：URDF 和 SRDF 教程

RobotState 包含有关机器人在某个时间点的信息，存储关节位置的矢量以及可选的速度和加速度。此信息可用于获取有关机器人的运动学信息，该信息取决于其当前状态，例如末端执行器的雅可比。

RobotState 还包含辅助函数，用于根据末端执行器位置（笛卡尔姿势）设置手臂位置并计算笛卡尔轨迹。

在此示例中，我们将演练将这些类与 Panda 一起使用的过程。

运行测试

Ros 启动启动文件以直接从 moveit_tutorials 运行代码：

roslaunch moveit_tutorials robot_model_and_robot_state_tutorial.launch

预期输出将采用以下形式。由于我们使用的是随机关节值，因此数字将不匹配：

输出情况为

ros.moveit_tutorials: Model frame: /panda_link0
ros.moveit_tutorials: Joint panda_joint1: 0.000000
ros.moveit_tutorials: Joint panda_joint2: 0.000000
ros.moveit_tutorials: Joint panda_joint3: 0.000000
ros.moveit_tutorials: Joint panda_joint4: 0.000000
ros.moveit_tutorials: Joint panda_joint5: 0.000000
ros.moveit_tutorials: Joint panda_joint6: 0.000000
ros.moveit_tutorials: Joint panda_joint7: 0.000000
ros.moveit_tutorials: Current state is not valid
ros.moveit_tutorials: Current state is valid
ros.moveit_tutorials: Translation:
-0.541498
-0.592805
 0.400443

ros.moveit_tutorials: Rotation:
-0.395039  0.600666 -0.695086
 0.299981 -0.630807 -0.715607
-0.868306 -0.491205 0.0690048

ros.moveit_tutorials: Joint panda_joint1: -2.407308
ros.moveit_tutorials: Joint panda_joint2: 1.555370
ros.moveit_tutorials: Joint panda_joint3: -2.102171
ros.moveit_tutorials: Joint panda_joint4: -0.011156
ros.moveit_tutorials: Joint panda_joint5: 1.100545
ros.moveit_tutorials: Joint panda_joint6: 3.230793
ros.moveit_tutorials: Joint panda_joint7: -2.651568
ros.moveit_tutorials: Jacobian:
    0.592805   -0.0500638    -0.036041     0.366761   -0.0334361     0.128712 -4.33681e-18
   -0.541498   -0.0451907    0.0417049    -0.231187    0.0403683   0.00288573  3.46945e-18
           0    -0.799172    0.0772022    -0.247151    0.0818336    0.0511662            0
           0     0.670056    -0.742222     0.349402    -0.748556    -0.344057    -0.695086
           0     -0.74231    -0.669976    -0.367232    -0.662737     0.415389    -0.715607
           1  4.89669e-12    0.0154256     0.862009     0.021077     0.842067    0.0690048

这里的教程我没有怎么看懂，所以我们直接从源码出发来分析这个过程具体发生了什么吧。

#include <ros/ros.h>

// MoveIt
#include <moveit/robot_model_loader/robot_model_loader.h>
#include <moveit/robot_model/robot_model.h>
#include <moveit/robot_state/robot_state.h>

int main(int argc, char** argv)
{
  ros::init(argc, argv, "robot_model_and_robot_state_tutorial");
  ros::AsyncSpinner spinner(1);
  spinner.start();

  robot_model_loader::RobotModelLoader robot_model_loader("robot_description");
  const moveit::core::RobotModelPtr& kinematic_model = robot_model_loader.getModel();
  ROS_INFO("Model frame: %s", kinematic_model->getModelFrame().c_str());

  // Using the :moveit_core:`RobotModel`, we can construct a
  // :moveit_core:`RobotState` that maintains the configuration
  // of the robot. We will set all joints in the state to their
  // default values. We can then get a
  // :moveit_core:`JointModelGroup`, which represents the robot
  // model for a particular group, e.g. the "panda_arm" of the Panda
  // robot.
  moveit::core::RobotStatePtr kinematic_state(new moveit::core::RobotState(kinematic_model));
  kinematic_state->setToDefaultValues();
  const moveit::core::JointModelGroup* joint_model_group = kinematic_model->getJointModelGroup("panda_arm");

  const std::vector<std::string>& joint_names = joint_model_group->getVariableNames();

  // Get Joint Values
  // ^^^^^^^^^^^^^^^^
  // We can retrieve the current set of joint values stored in the state for the Panda arm.
  std::vector<double> joint_values;
  kinematic_state->copyJointGroupPositions(joint_model_group, joint_values);
  for (std::size_t i = 0; i < joint_names.size(); ++i)
  {
    ROS_INFO("Joint %s: %f", joint_names[i].c_str(), joint_values[i]);
  }

  // Joint Limits
  // ^^^^^^^^^^^^
  // setJointGroupPositions() does not enforce joint limits by itself, but a call to enforceBounds() will do it.
  /* Set one joint in the Panda arm outside its joint limit */
  joint_values[0] = 5.57;
  kinematic_state->setJointGroupPositions(joint_model_group, joint_values);

  /* Check whether any joint is outside its joint limits */
  ROS_INFO_STREAM("Current state is " << (kinematic_state->satisfiesBounds() ? "valid" : "not valid"));

  /* Enforce the joint limits for this state and check again*/
  kinematic_state->enforceBounds();
  ROS_INFO_STREAM("Current state is " << (kinematic_state->satisfiesBounds() ? "valid" : "not valid"));

  // Forward Kinematics
  // ^^^^^^^^^^^^^^^^^^
  // Now, we can compute forward kinematics for a set of random joint
  // values. Note that we would like to find the pose of the
  // "panda_link8" which is the most distal link in the
  // "panda_arm" group of the robot.
  kinematic_state->setToRandomPositions(joint_model_group);
  const Eigen::Isometry3d& end_effector_state = kinematic_state->getGlobalLinkTransform("panda_link8");

  /* Print end-effector pose. Remember that this is in the model frame */
  ROS_INFO_STREAM("Translation: \n" << end_effector_state.translation() << "\n");
  ROS_INFO_STREAM("Rotation: \n" << end_effector_state.rotation() << "\n");

  // Inverse Kinematics
  // ^^^^^^^^^^^^^^^^^^
  // We can now solve inverse kinematics (IK) for the Panda robot.
  // To solve IK, we will need the following:
  //
  //  * The desired pose of the end-effector (by default, this is the last link in the "panda_arm" chain):
  //    end_effector_state that we computed in the step above.
  //  * The timeout: 0.1 s
  double timeout = 0.1;
  bool found_ik = kinematic_state->setFromIK(joint_model_group, end_effector_state, timeout);

  // Now, we can print out the IK solution (if found):
  if (found_ik)
  {
    kinematic_state->copyJointGroupPositions(joint_model_group, joint_values);
    for (std::size_t i = 0; i < joint_names.size(); ++i)
    {
      ROS_INFO("Joint %s: %f", joint_names[i].c_str(), joint_values[i]);
    }
  }
  else
  {
    ROS_INFO("Did not find IK solution");
  }

  // Get the Jacobian
  // ^^^^^^^^^^^^^^^^
  // We can also get the Jacobian from the :moveit_core:`RobotState`.
  Eigen::Vector3d reference_point_position(0.0, 0.0, 0.0);
  Eigen::MatrixXd jacobian;
  kinematic_state->getJacobian(joint_model_group,
                               kinematic_state->getLinkModel(joint_model_group->getLinkModelNames().back()),
                               reference_point_position, jacobian);
  ROS_INFO_STREAM("Jacobian: \n" << jacobian << "\n");
  // END_TUTORIAL

  ros::shutdown();
  return 0;
}

这里我已经有点感觉了，如何通过关节和连杆信息来进行运动学的计算，首先link连杆是刚性不见，joint关节式用来连接两个link的，允许相对运动，包括旋转运动和移动关节两种基础形式，模型坐标系一般是不动的那个底座。

2. Model Frame（模型坐标系）

机器人模型的 "根坐标系"，固定在机器人的基座（通常是link0）上，所有其他连杆的位置和姿态都以这个坐标系为基准计算。

例子：panda_link0 的坐标系就是模型坐标系，机械臂所有运动都相对于这个坐标系计算。

3. Robot Model（机器人模型）

机器人的 "蓝图"，包含所有静态信息：

每个关节的类型（旋转 / 移动）、限位（比如旋转关节的角度范围：-2.9 到 2.9 弧度）、名称（panda_joint1到panda_joint7）。

每个连杆的长度、质量、形状，以及连杆之间通过哪个关节连接（比如link1通过joint1连接link0）。

这些信息通常通过 URDF/Xacro 文件定义，ROS 通过robot_description参数加载。

4. Robot State（机器人状态）

机器人的 "当前姿势"，记录所有关节的当前位置（比如每个旋转关节的角度）。

例如：7 关节机械臂的状态就是一个包含 7 个数值的列表 [θ1, θ2, θ3, θ4, θ5, θ6, θ7]，分别对应 7 个关节的当前角度。

有了状态，就能计算出每个连杆（包括末端执行器）的位置和姿态。

过程

初始化

首先加载了模型并初始化状态信息

// 加载机器人模型（从robot_description参数）
robot_model_loader::RobotModelLoader robot_model_loader("robot_description");
const moveit::core::RobotModelPtr& kinematic_model = robot_model_loader.getModel();
// 模型坐标系（比如panda_link0）
ROS_INFO("Model frame: %s", kinematic_model->getModelFrame().c_str());

// 创建机器人状态（基于模型，初始关节值为默认值，比如全0）
moveit::core::RobotStatePtr kinematic_state(new moveit::core::RobotState(kinematic_model));
kinematic_state->setToDefaultValues();  // 关节值设为默认（比如全0）

// 获取关节组（比如"panda_arm"，包含7个关节）
const moveit::core::JointModelGroup* joint_model_group = kinematic_model->getJointModelGroup("panda_arm");

关节限位信息

第二步给定了关键限位检查

// 获取当前关节值（7个关节的角度）
std::vector<double> joint_values;  // 存储7个数值
kinematic_state->copyJointGroupPositions(joint_model_group, joint_values);
// 打印每个关节的名称和当前角度（默认值）
for (std::size_t i = 0; i < joint_names.size(); ++i) {
  ROS_INFO("Joint %s: %f", joint_names[i].c_str(), joint_values[i]);
}

// 故意设置一个关节超出限位（比如joint1的限位是-2.9到2.9，设为5.57）
joint_values[0] = 5.57;  // 第一个关节（joint1）角度
kinematic_state->setJointGroupPositions(joint_model_group, joint_values);

// 检查是否超出限位（此时返回not valid）
ROS_INFO_STREAM("Current state is " << (kinematic_state->satisfiesBounds() ? "valid" : "not valid"));

// 自动修正到限位内（比如5.57→2.9）
kinematic_state->enforceBounds();
// 再次检查（返回valid）
ROS_INFO_STREAM("Current state is " << (kinematic_state->satisfiesBounds() ? "valid" : "not valid"));

每个关节的参数：这里主要关注 "限位"（关节能转动的最大 / 最小角度），模型中已定义，状态会根据限位校验和修正关节值。

FK

第三步，正向运动学，正向的意思就是从关节角度计算末端执行器的位置，也就是输入了当前7个关节的角度（θ1~θ7），计算末端执行器（比如panda_link8）在模型坐标系（link0）中的位置和姿态。

// 给7个关节随机设置一个合法角度（在限位内）
kinematic_state->setToRandomPositions(joint_model_group);

// 计算末端执行器（panda_link8）的位姿
const Eigen::Isometry3d& end_effector_state = kinematic_state->getGlobalLinkTransform("panda_link8");

// 打印结果：平移（x,y,z）和旋转（3x3矩阵）
ROS_INFO_STREAM("Translation: \n" << end_effector_state.translation() << "\n");  // 位置
ROS_INFO_STREAM("Rotation: \n" << end_effector_state.rotation() << "\n");      // 姿态

正运动学应该怎么计算呢？

通过坐标变换链计算：

link0 到 link1：通过 joint1 的角度 θ1 计算 link1 相对于 link0 的位姿。

link1 到 link2：通过 joint2 的角度 θ2 计算 link2 相对于 link1 的位姿，再叠加到 link0 坐标系。

以此类推，直到计算出 link8 相对于 link0 的位姿（末端位姿）。

每一步的变换都用齐次变换矩阵（4x4）表示，最终通过矩阵乘法叠加得到末端位姿。

IK

第四步，逆向运动学------从末端执行器位姿来计算关节角

已知末端执行器（link8）的目标位姿（比如想让末端到达 (x=0.5, y=0, z=0.3) 且旋转姿态为某个值），求 7 个关节的角度（θ1~θ7）。

// 目标位姿：用FK得到的末端位姿作为目标（也可以手动设置）
double timeout = 0.1;  // 求解超时时间（100毫秒）
// 尝试求解IK
bool found_ik = kinematic_state->setFromIK(joint_model_group, end_effector_state, timeout);

// 打印结果
if (found_ik) {
  // 提取求解得到的7个关节角
  kinematic_state->copyJointGroupPositions(joint_model_group, joint_values);
  for (std::size_t i = 0; i < joint_names.size(); ++i) {
    ROS_INFO("Joint %s: %f", joint_names[i].c_str(), joint_values[i]);
  }
} else {
  ROS_INFO("Did not find IK solution");  // 目标位姿太离谱，解不出来
}

IK要比FK复杂，因为7个关节对应6个末端自由度，（x,y,z 平移 + 3 个旋转），是超静定问题（多解或者无解）。代码中一般用数值迭代法（牛顿法）

从一个初始关节角（比如当前角度）出发，计算其对应的末端位姿（用 FK）。

计算与目标位姿的误差（比如位置差、角度差）。

逐步调整关节角，减小误差，直到误差小于阈值或超时。

注意：

所有 7 个关节都会被调整，因为它们共同决定末端位姿。

若目标位姿超出机械臂工作空间（比如太近或太远），则无解。

雅可比矩阵------关节速度与末端速度的关系

什么是雅可比矩阵？一个 6x7 的矩阵（6 行：末端 3 个平移速度 + 3 个旋转速度；7 列：7 个关节的角速度），描述 "关节速度如何影响末端速度"：

末端速度 = 雅可比矩阵 × 关节速度

// 参考点：末端执行器坐标系原点（0,0,0）
Eigen::Vector3d reference_point_position(0.0, 0.0, 0.0);
Eigen::MatrixXd jacobian;  // 存储雅可比矩阵（6x7）

// 计算雅可比矩阵
kinematic_state->getJacobian(joint_model_group,
                             kinematic_state->getLinkModel(joint_model_group->getLinkModelNames().back()),
                             reference_point_position, jacobian);
ROS_INFO_STREAM("Jacobian: \n" << jacobian << "\n");

基于当前关节角（状态）和机器人结构（模型）计算：

每一列对应一个关节：若关节 i 转动 1 弧度 / 秒，末端会产生多大的平移和旋转速度，这列数值就是这个速度的分量。

用途：运动控制（比如让末端按特定速度移动，反推关节需要转多快）、 singularities（奇异点）检测（矩阵行列式为 0 时，末端某些方向动不了）。

这里我们举个例子来说明雅可比矩阵是怎么和模型相互作用的。

实际在moveit中，通过调用API来计算这个J矩阵即可。

总结关键问题

7 个关节都会被考虑吗？会！FK/IK/ 雅可比计算都基于关节组（7 个关节），所有关节的角度共同决定末端位姿。

末端执行器panda_link8是什么？机械臂最末端的连杆（法兰盘），用来安装夹爪等工具，是我们关注的 "操作端点"，FK/IK 都是以它为目标。

模型、状态、关节、连杆的关系？

模型（蓝图）定义了关节和连杆的 "结构"（谁连谁，能转多大）。

状态（姿势）记录了关节的 "当前角度"。

有了结构和角度，就能算连杆（包括末端）的位姿（FK），或反过来算角度（IK）。

到此为止，moveit的基本教程就算是结束了，后续我们会自己做一些项目的开发时还会回顾这些基本知识。同时也附上另外一位博主的相关教程，https://blog.csdn.net/huangjunsheng123/category_10446765.html