Bayes/BO-CNN-LSTM、CNN-LSTM、LSTM三模型多变量回归预测Matlab

基于 MATLAB 的深度学习回归预测项目，集成了多种神经网络模型并进行性能比较。以下是对代码的详细分析：

主要功能

• 多模型回归预测：实现LSTM、CNN-LSTM和贝叶斯优化的CNN-LSTM三种模型
• 自动化超参数优化：使用贝叶斯优化算法自动寻找最佳网络参数
• 综合性能评估：通过多种可视化图表和指标全面评估模型性能

算法步骤

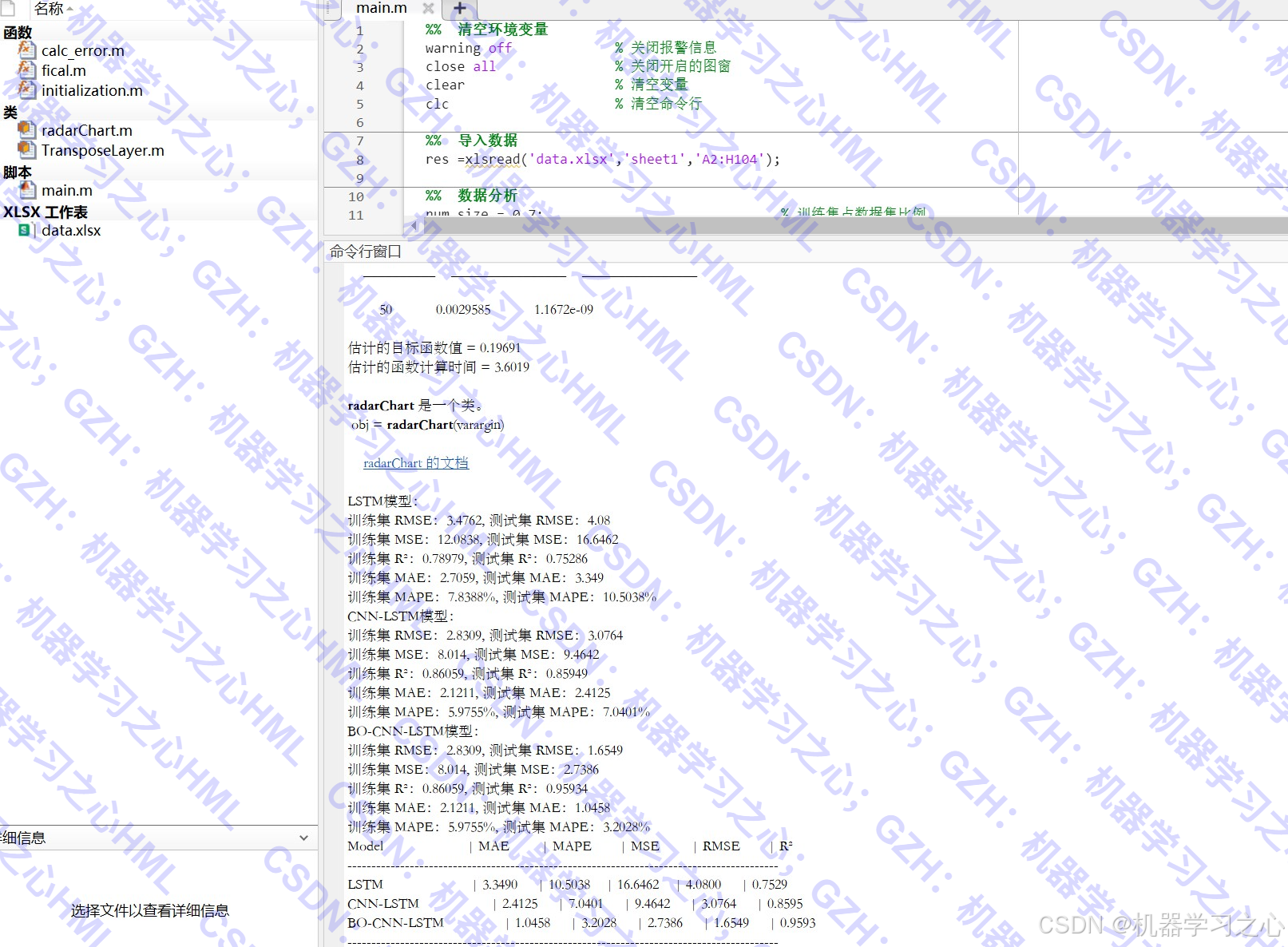
1. 数据预处理

- 数据导入与清洗
- 训练集/测试集划分(70%/30%)
- 数据归一化(mapminmax)
- 数据格式重塑(适应网络输入)

2. 模型构建与训练

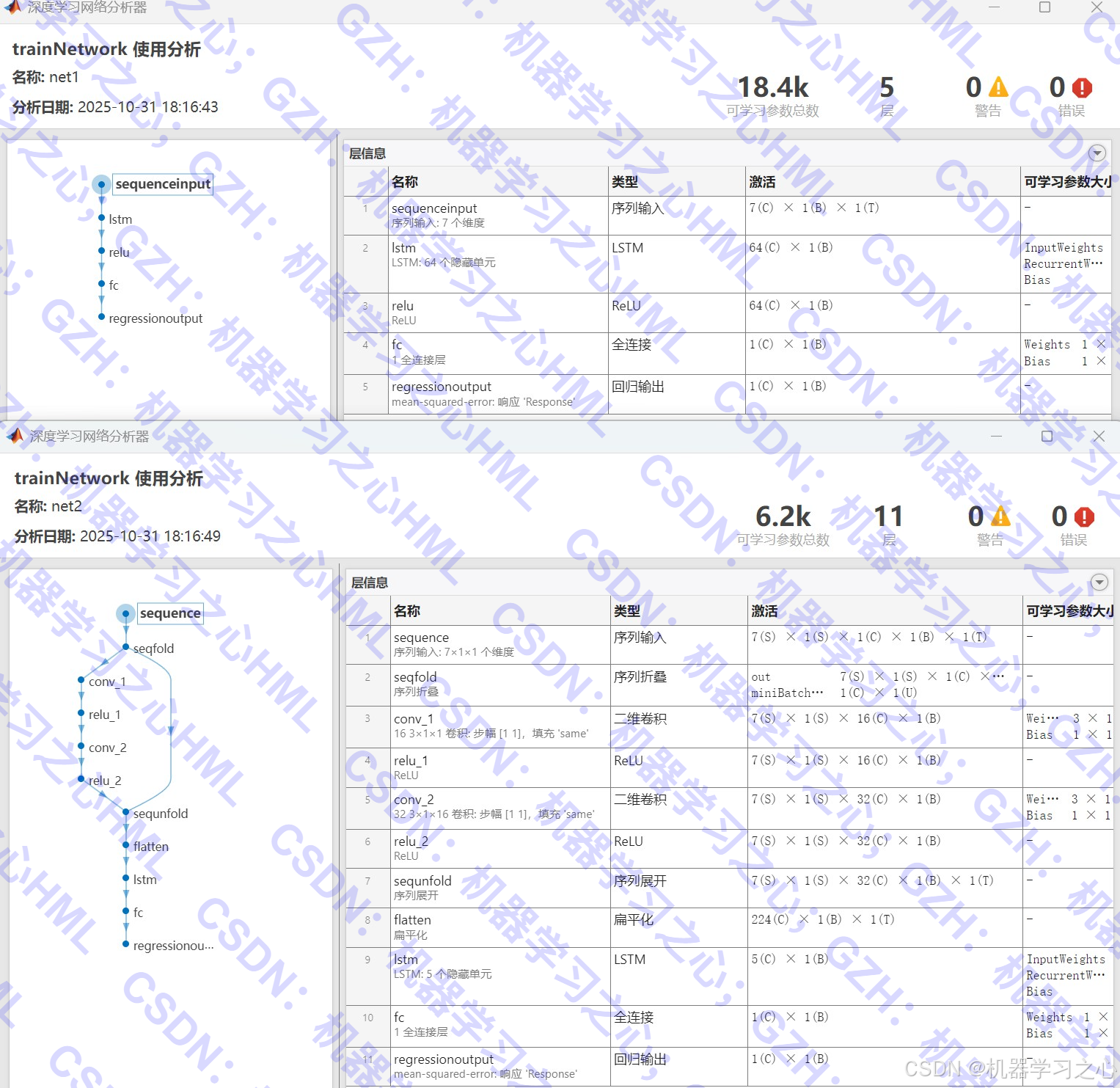
LSTM模型：

• 输入层 → LSTM层(64单元) → ReLU → 全连接层 → 回归层

CNN-LSTM模型：

• 序列折叠 → 2D卷积(16,32个滤波器) → ReLU → 序列反折叠 → LSTM(5单元) → 全连接

BO-CNN-LSTM模型：

• 使用贝叶斯优化确定：隐藏单元数、学习率、L2正则化系数

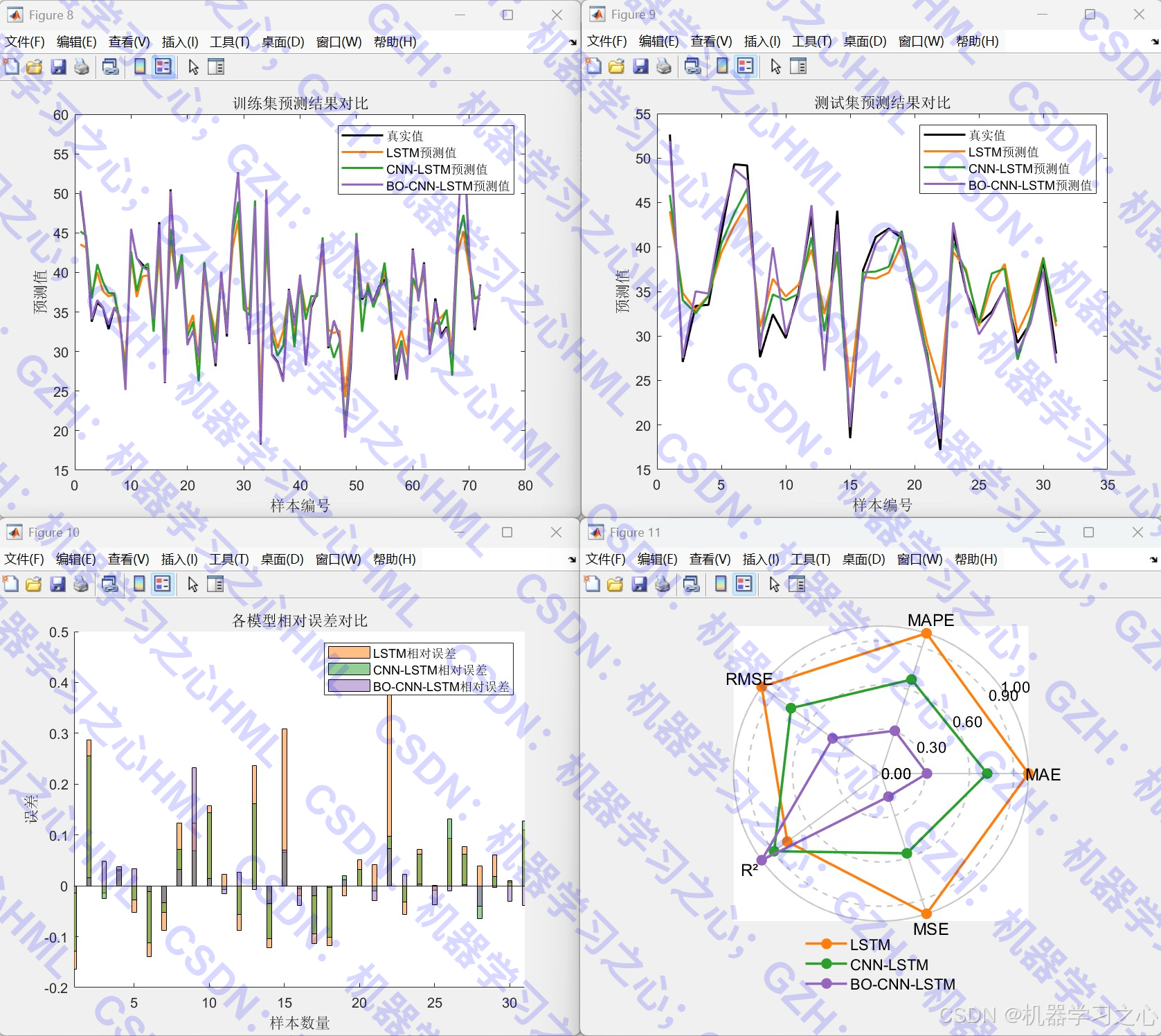
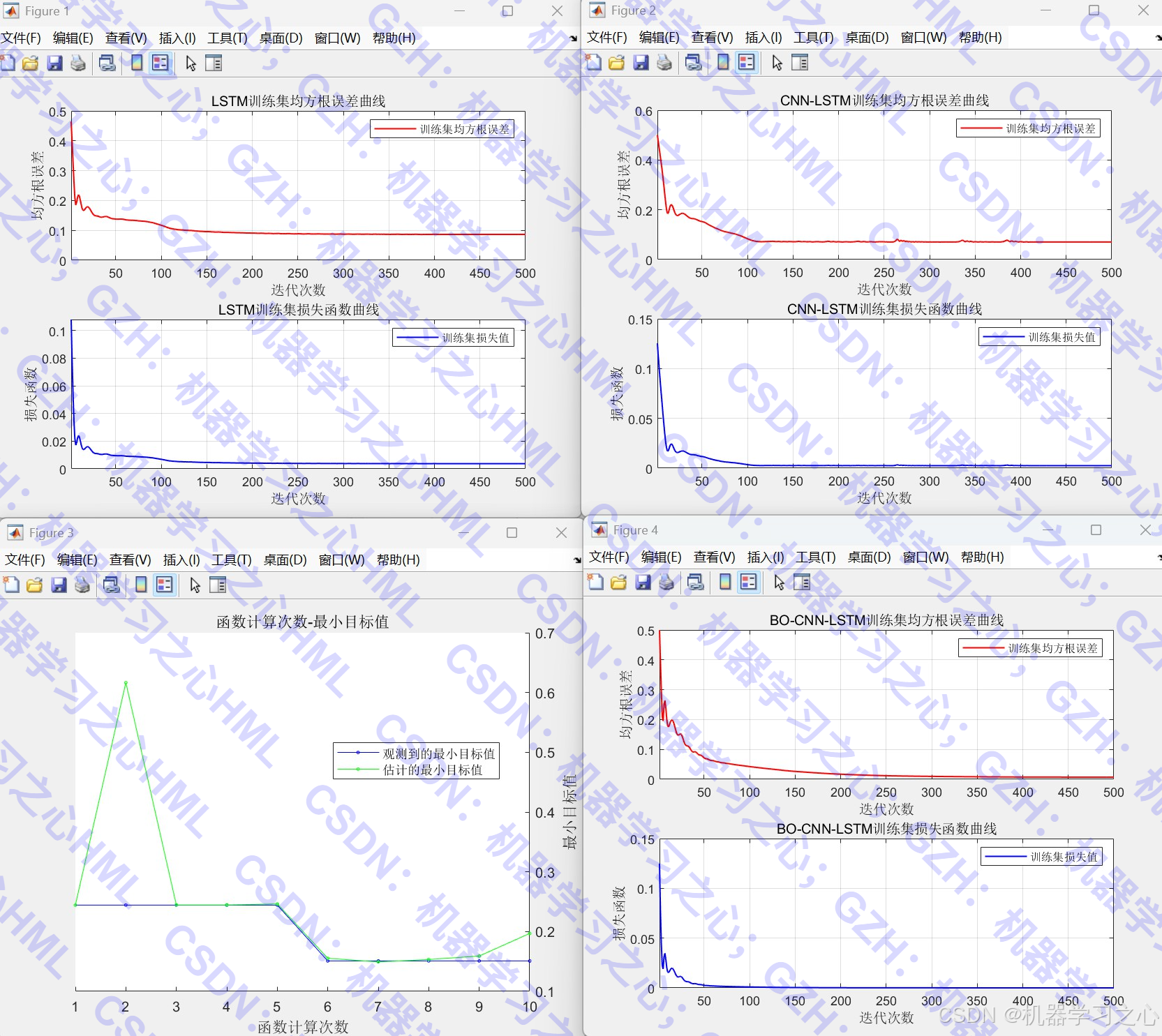
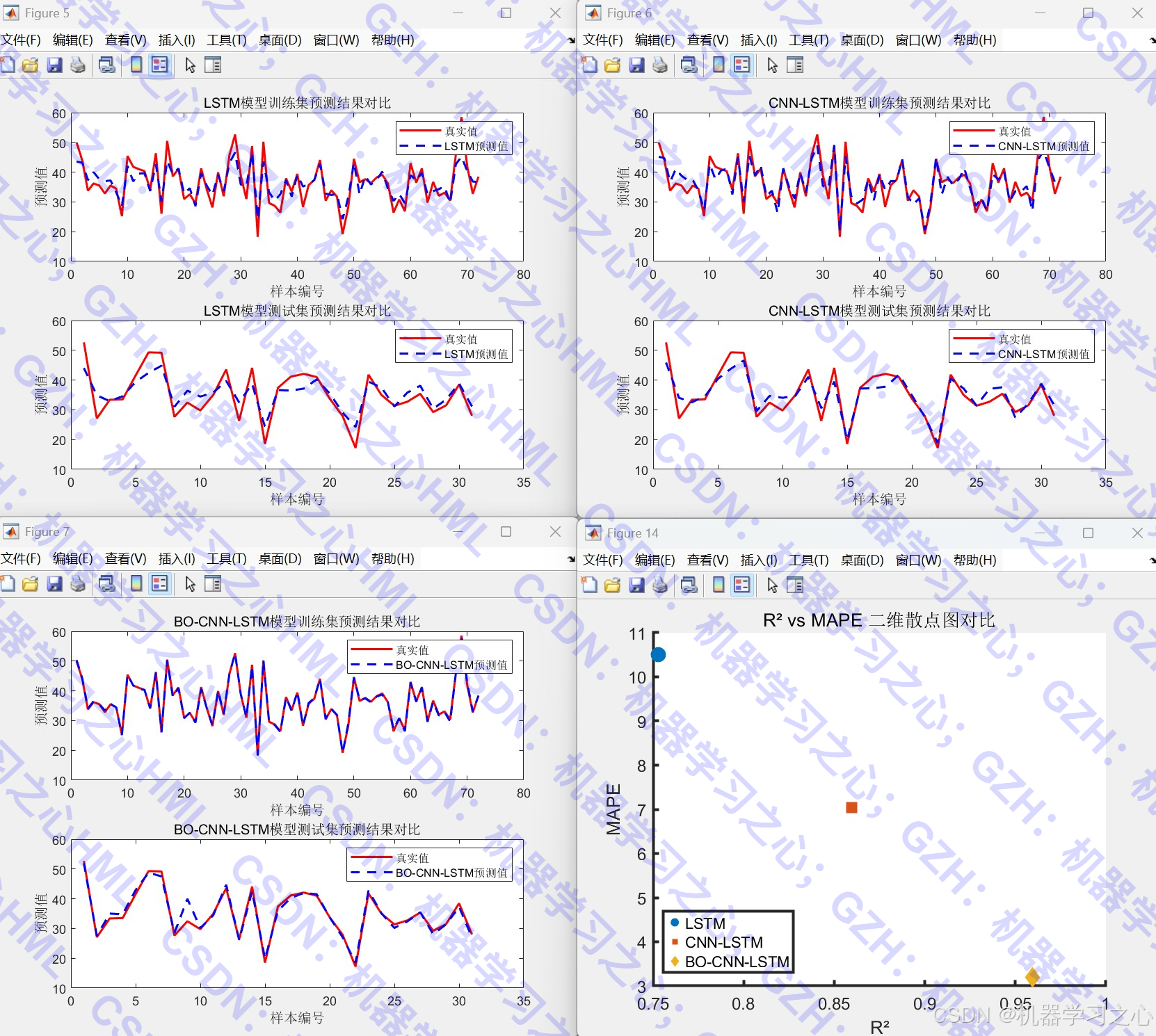
3. 模型评估与可视化

• 损失函数曲线
• 预测结果对比图
• 误差分析图
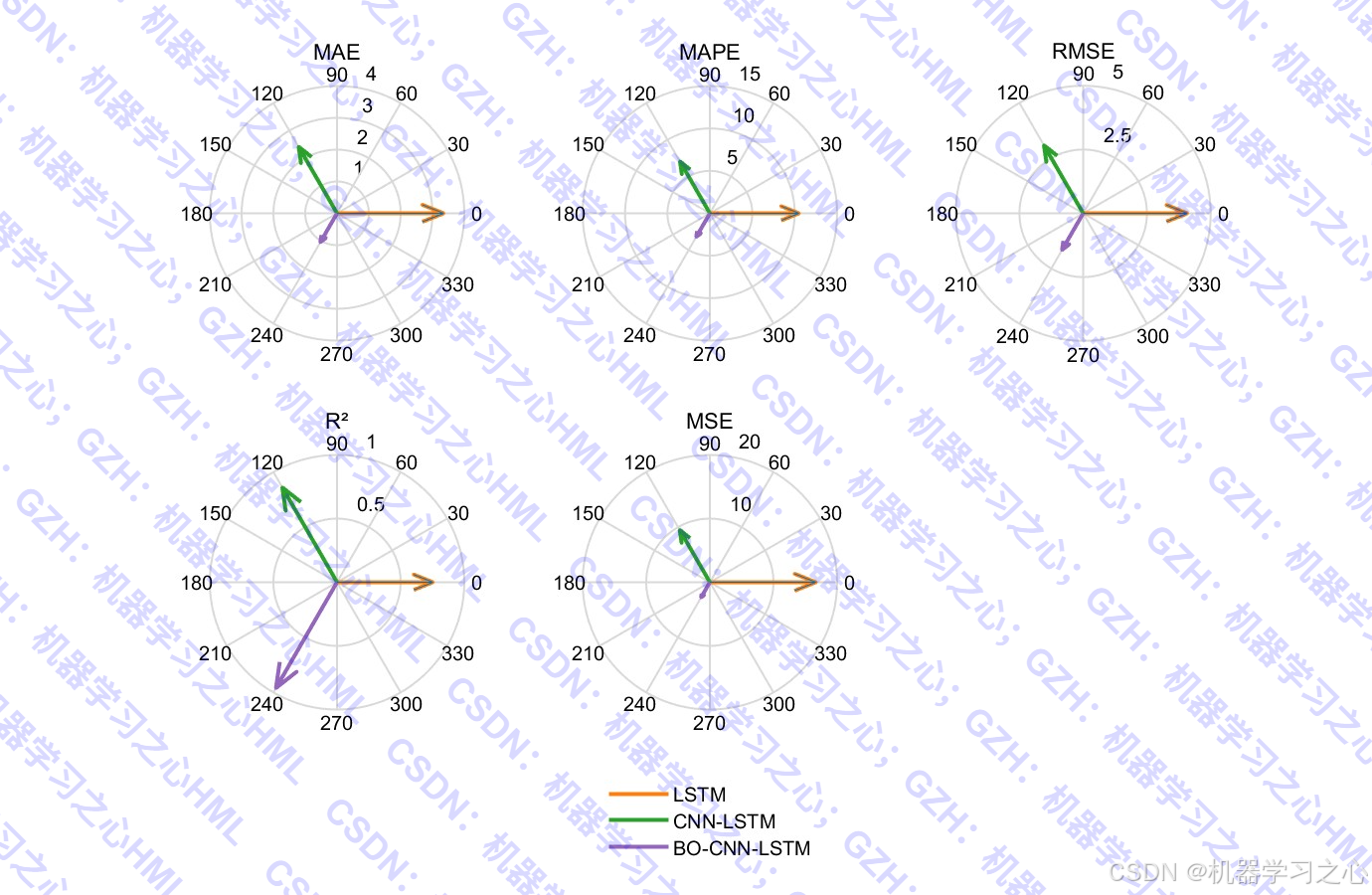
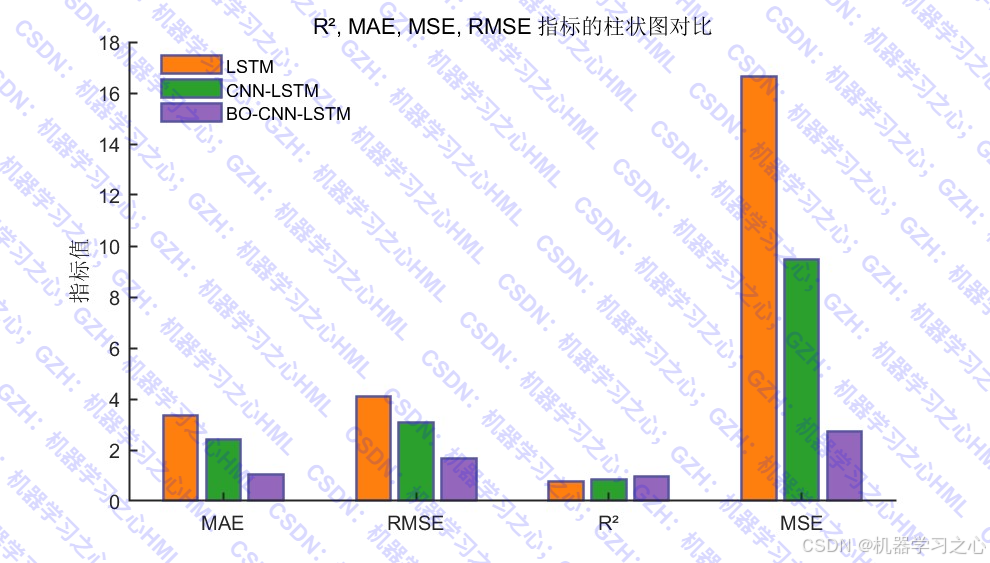
• 多种性能图表(雷达图、罗盘图、柱状图等)

技术路线

数据预处理 → 基准LSTM → CNN-LSTM改进 → 贝叶斯优化调参 → 综合性能对比

核心公式原理

LSTM单元

遗忘门:ft=σ(Wf⋅[ht−1,xt]+bf) 遗忘门: f_t = σ(W_f·[h_{t-1}, x_t] + b_f) 遗忘门:ft=σ(Wf⋅[ht−1,xt]+bf)
输入门:it=σ(Wi⋅[ht−1,xt]+bi) 输入门: i_t = σ(W_i·[h_{t-1}, x_t] + b_i) 输入门:it=σ(Wi⋅[ht−1,xt]+bi)
候选值:C~t=tanh(WC⋅[ht−1,xt]+bC) 候选值: C̃_t = tanh(W_C·[h_{t-1}, x_t] + b_C) 候选值:C~t=tanh(WC⋅[ht−1,xt]+bC)
细胞状态:Ct=ft⊙Ct−1+it⊙C~t 细胞状态: C_t = f_t ⊙ C_{t-1} + i_t ⊙ C̃_t 细胞状态:Ct=ft⊙Ct−1+it⊙C~t
输出门:ot=σ(Wo⋅[ht−1,xt]+bo) 输出门: o_t = σ(W_o·[h_{t-1}, x_t] + b_o) 输出门:ot=σ(Wo⋅[ht−1,xt]+bo)
隐藏状态:ht=ot⊙tanh(Ct) 隐藏状态: h_t = o_t ⊙ tanh(C_t) 隐藏状态:ht=ot⊙tanh(Ct)

卷积操作

Y(i,j)=∑∑X(i+m,j+n)⋅K(m,n)+b Y(i,j) = ∑∑ X(i+m, j+n)·K(m,n) + b Y(i,j)=∑∑X(i+m,j+n)⋅K(m,n)+b

评价指标

• RMSE : 1n∑i=1n(yi−y^i)2\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}n1∑i=1n(yi−y^i)2
• MAE : 1n∑i=1n∣yi−y^i∣\frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y}_i|n1∑i=1n∣yi−y^i∣
• MAPE : 100%n∑i=1n∣yi−y^iyi∣\frac{100\%}{n}\sum_{i=1}^{n}\left|\frac{y_i - \hat{y}_i}{y_i}\right|n100%∑i=1n yiyi−y^i
• R² : 1−∑(yi−y^i)2∑(yi−yˉ)21 - \frac{\sum(y_i - \hat{y}_i)^2}{\sum(y_i - \bar{y})^2}1−∑(yi−yˉ)2∑(yi−y^i)2

参数设定

训练参数

- 最大训练轮次: 500
- 初始学习率: 0.01(LSTM), 3e-3(CNN-LSTM)
- 学习率下降: 400轮后×0.1
- L2正则化: 1e-2(LSTM), 4e-3(CNN-LSTM)
- 优化器: Adam

贝叶斯优化范围

- 隐藏单元数: [10, 50]
- 学习率: [1e-3, 1] (对数变换)
- L2正则化: [1e-10, 1e-2] (对数变换)
- 最大评估次数: 10

运行环境要求

• MATLAB版本: R2020b或更高

应用场景

适用领域

2. 能源负荷: 电力需求预测
3. 工业制造: 设备故障预测、质量预测
4. 气象预报: 温度、降水量预测
5. 交通流量: 道路拥堵预测

数据要求

• 输入特征维度: 7维(可调整)
• 输出维度: 1维(回归问题)

优势特点

• 自动化调参: 减少人工调参工作量
• 模型对比: 提供全面的性能评估
• 可视化丰富: 多种图表直观展示结果
• 模块化设计 : 易于扩展和修改
  
  
  
  
  
  
  

完整代码私信回复Bayes/BO-CNN-LSTM、CNN-LSTM、LSTM三模型多变量回归预测Matlab