TARJAN 是什么
TARJAN 是一种图论算法,可以高效的求出强连通分量等,便于求最长路、DAG 、割点和桥等。
TARJAN 怎么做
DFS 序
在此之前,我们要先学习图的 DFS 序。对于一个图,我们选择一个点为树根,然后做 DFS ,按照访问的次序给每个点标记 DFS 序。因为有些点可能访问不到,所以就要遍历所有点,如果访问的点没有求过 DFS 序,就以他为树根求一次。
伪代码:
cpp
dfs(int now)
{
dfn[i] = ++nowdfn;
for(auto i : pict[now])
{
if(!dfn[i])
{
dfs(i);
}
}
}
for(int i = 1;i <= n;i++) if(!dfn[i]) dfs(i);强连通分量(TARJAN)
对于一个有向图,如果图中所有点两两可达,则这个图称为强连通图。一个图的极大强联通子图称为强连通分量,这里的极大强连通子图意为这个子图无法继续在扩大的同时保持强连通。如图:
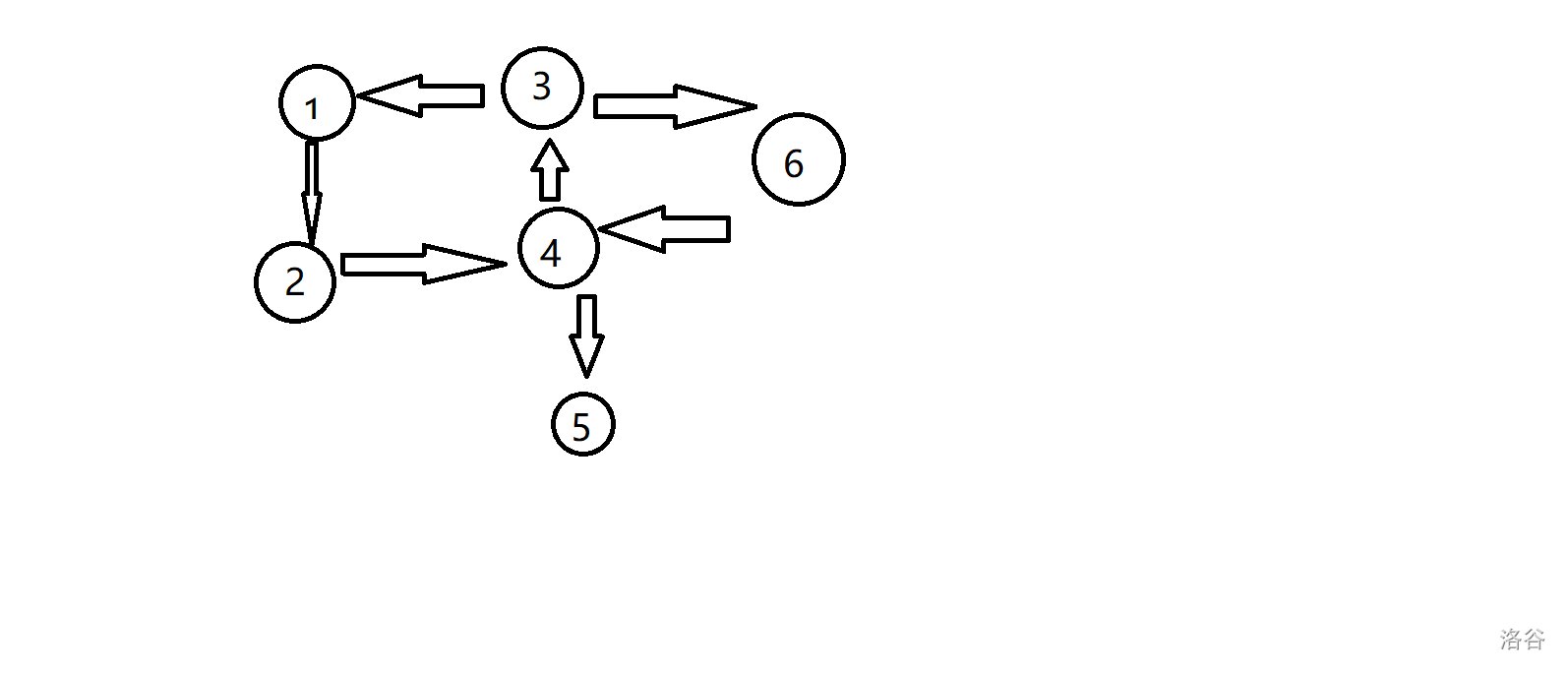
图丑
图中的强连通分量有 { 1 , 2 , 3 , 4 , 6 } \{1,2,3,4,6\} {1,2,3,4,6} 和 { 5 } \{5\} {5} 。虽然 { 1 , 2 , 3 , 4 } \{1,2,3,4\} {1,2,3,4}、 { 3 , 4 , 6 } \{3,4,6\} {3,4,6} 也是强连通子图,但他们都不是极大的,是可以扩展的。
求强连通分量,我们需要一个值 l o w low low ,表示当前点能走到的 DFS 序最小的点的 DFS 序。对此,我们需要把图中的树边、返祖边和横叉边找出来。
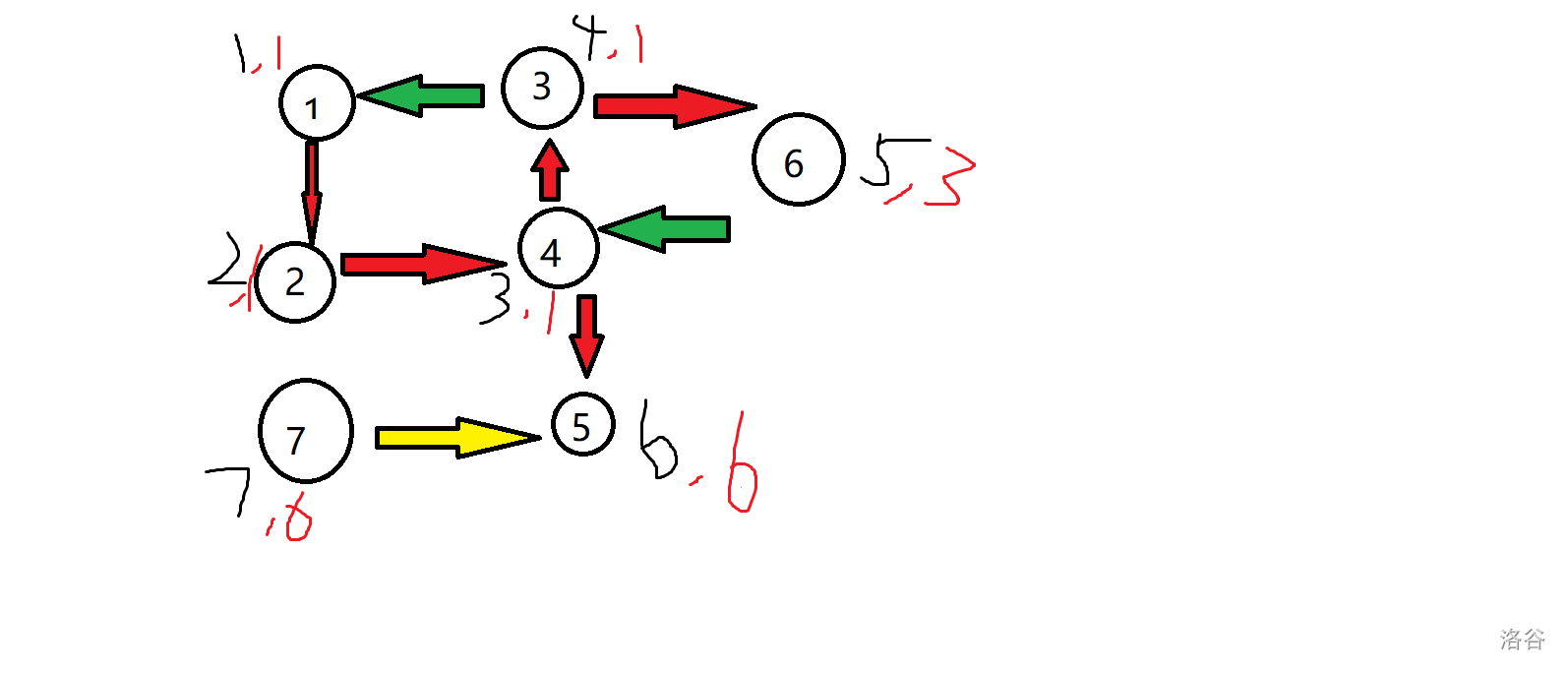
如图,红色的是树边,绿色的是返祖边,黄色的是横叉边。节点外黑色的数是 DFS 序,红色的是 l o w low low 。
可以看出,树边是在 DFS 过程中访问一个未访问过的节点的边。如果在 DFS 过程遇到一条树边,则直接把 l o w n o w = min ( l o w n o w , l o w i ) low_{now}=\min(low_{now},low_i) lownow=min(lownow,lowi) 即可。
对于返祖边,意思就是 DFS 过程中遇到自己的祖先的边。那么这就说明形成了一个环。这时不应该与 l o w i low_i lowi 比较,而应该与 d f n i dfn_i dfni 比较。
对于横叉边,我们知道这是在两棵树之间的边,这时这条边没有意义,直接忽略。
然后我们发现 d f n 1 = l o w 1 dfn_1 = low_1 dfn1=low1 ,说明有一个包含 1 1 1 的强连通分量,很显然我们需要求出有哪些点位于这个强连通分量中。这里我们需要用栈来实现。每访问一个点 n o w now now 就把这个点入栈,点 n o w now now 的儿子访问完后如果 d f n n o w = l o w n o w dfn_{now} = low_{now} dfnnow=lownow 就不断出栈知道把 n o w now now 出栈,然后出栈的所有点处于同一个强连通分量中。
如果发现点 i i i 被访问过,那么边 ( n o w , i ) (now,i) (now,i) 是一条返祖边或横叉边,否则是一条树边。对于返祖边或横叉边,我们只需要看看 i i i 是否在栈中即可。因为如果 i i i 不在栈中,那么它肯定不在 n o w now now 所在的树上。
对于刚才的图实现如下:
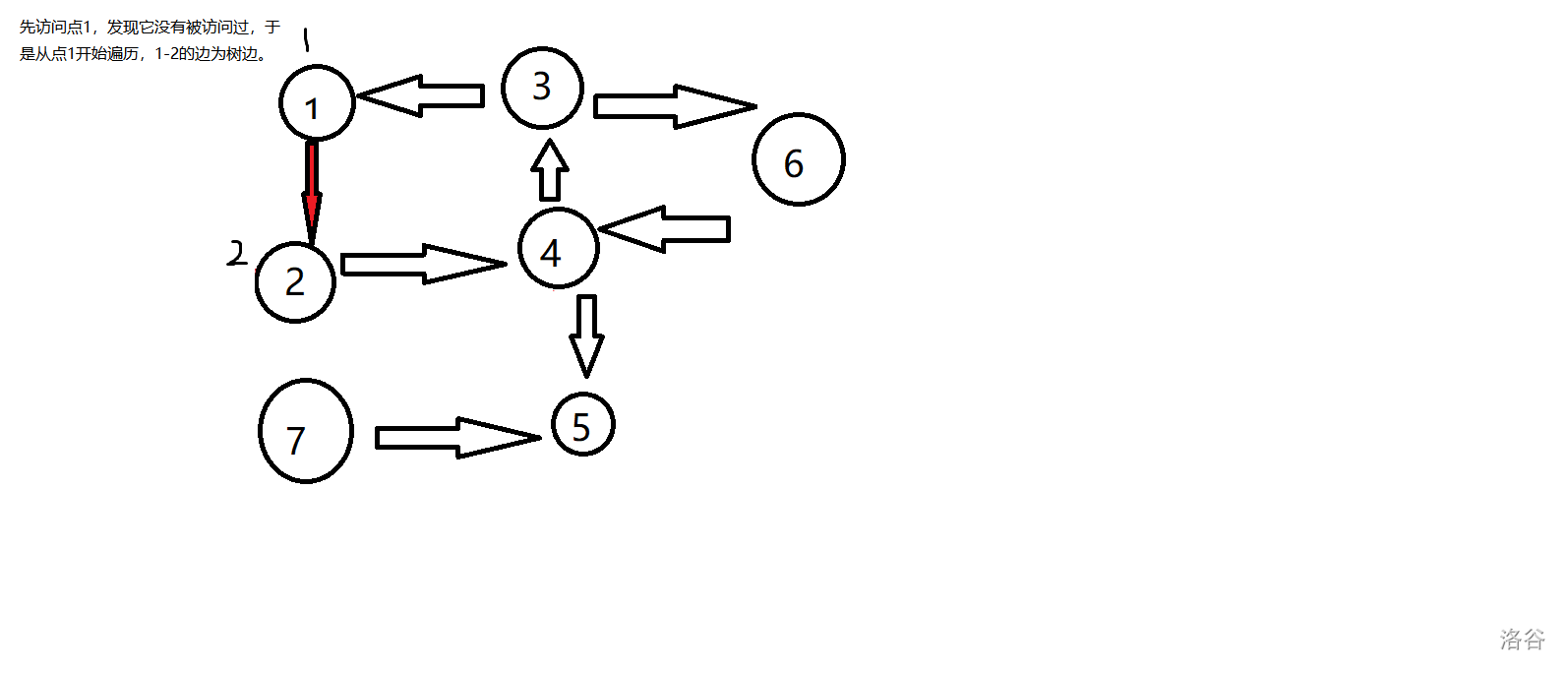
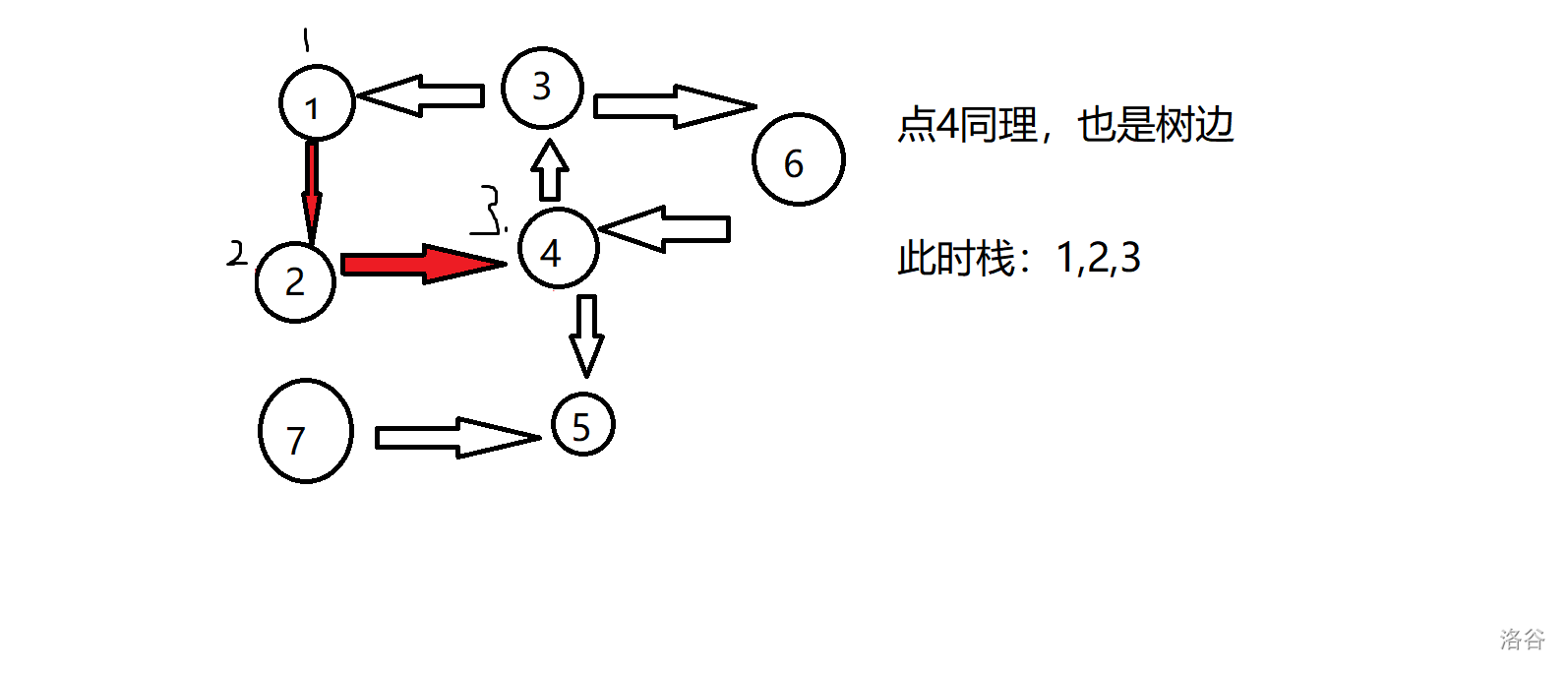
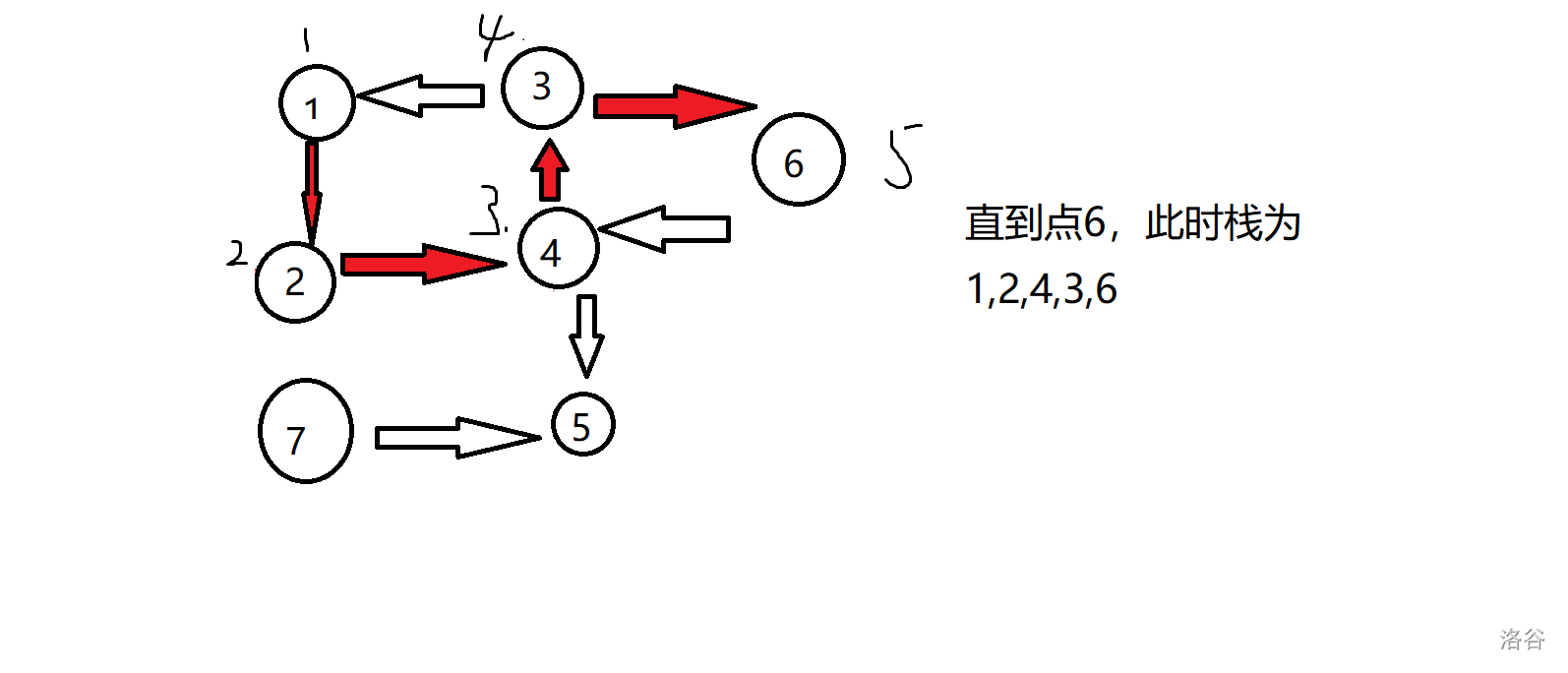
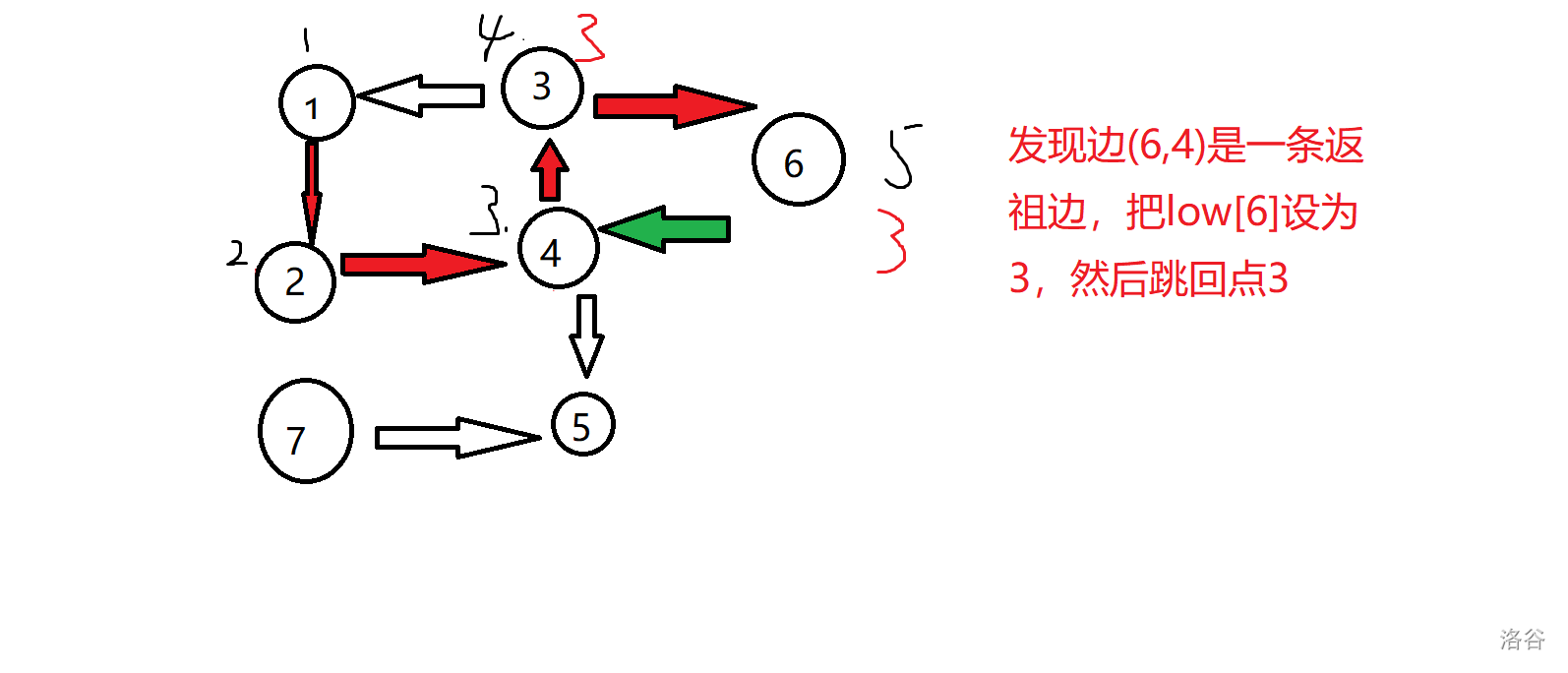
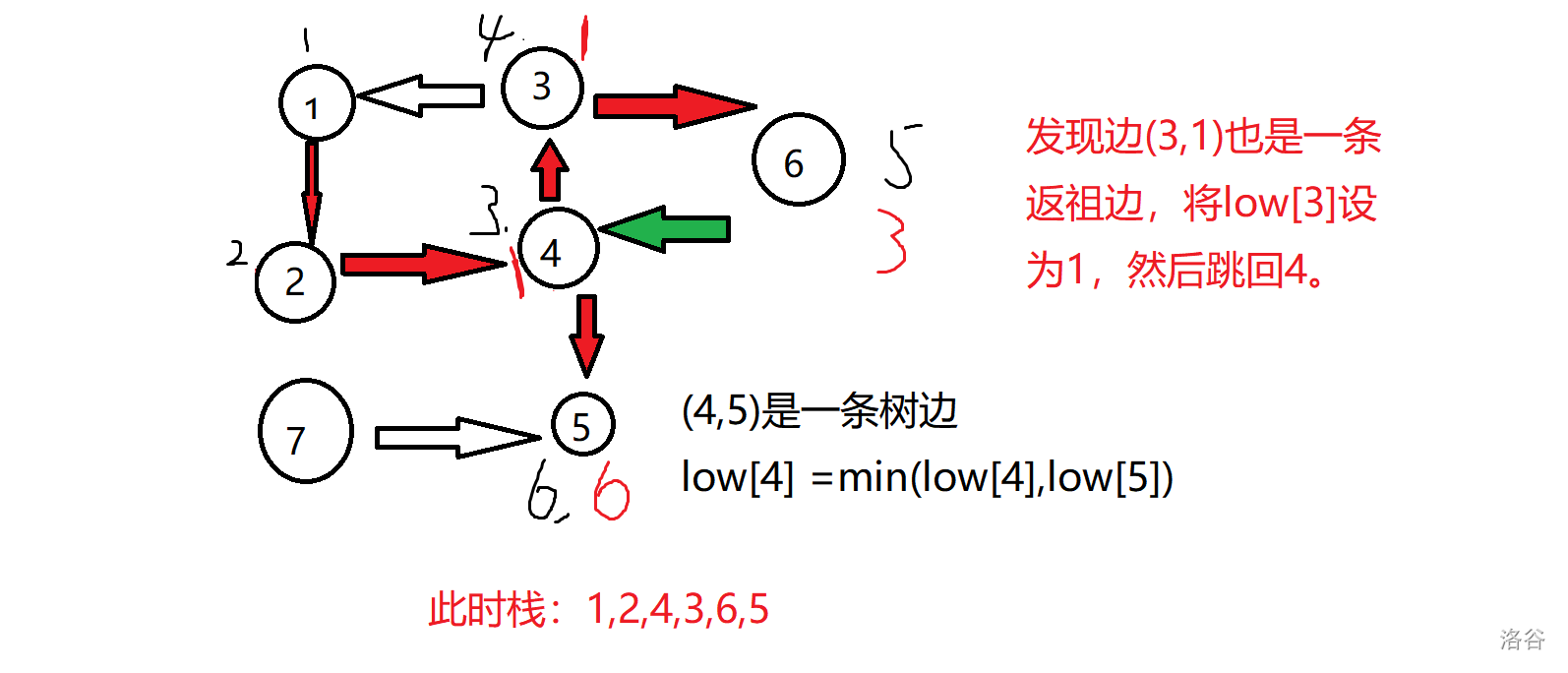
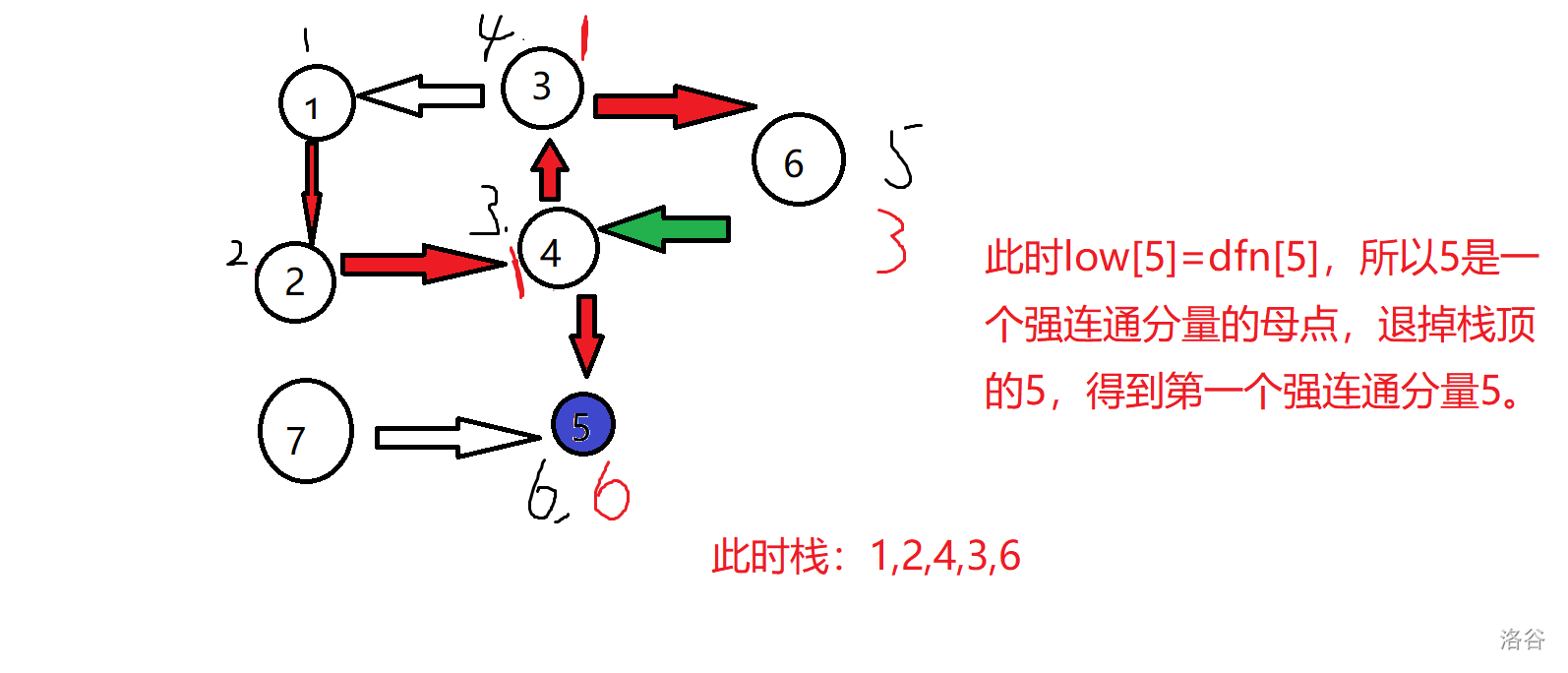
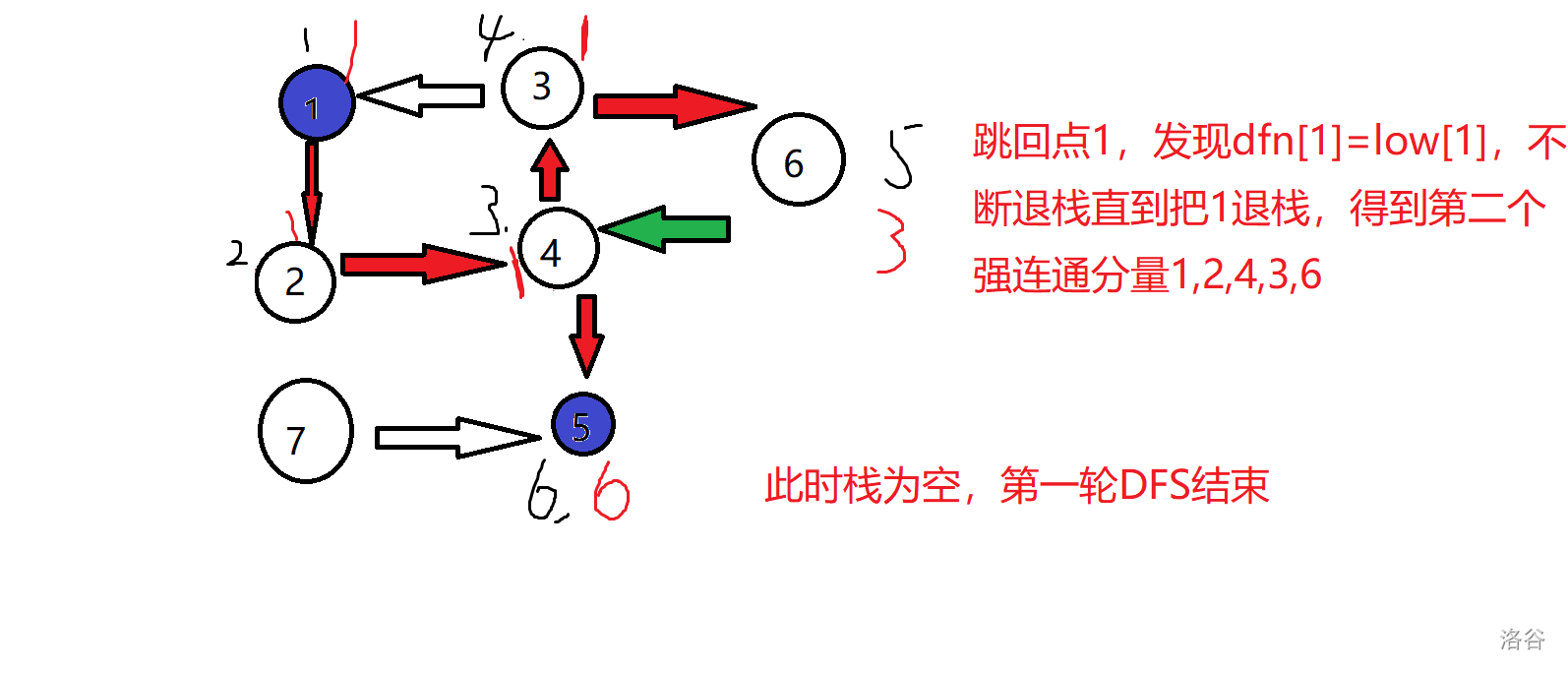
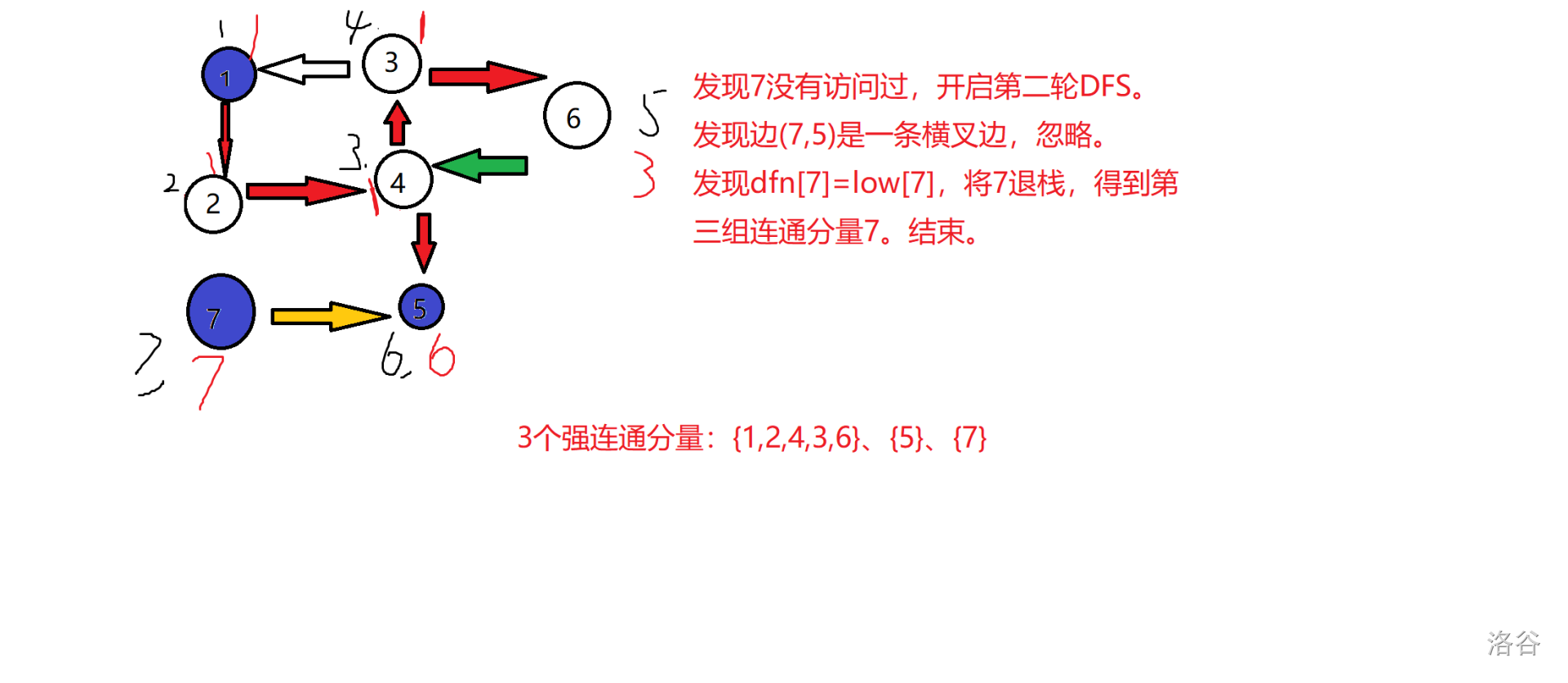
锅:边(3,1)忘记染色了
过程简单明了,如果还不懂就自己把图画一遍。
代码实现如下:
cpp
void tarjan(int now)
{
dfn[now] = low[now] = nowdfn++;
vis.push(now);
visited[now] = 1;
for(auto i : pict[now])
{
if(!dfn[i])
{
tarjan(i);
low[now] = min(low[now],low[i]);
}
else if(visited[i]) low[now] = min(low[now],dfn[i]);
}
if(dfn[now] == low[now])
{
scs++;
while(vis.top() != now)
{
siz[scs]++;
scc[vis.top()] = scs;
visited[vis.top()] = 0;
vis.pop();
}
siz[scs]++;
scc[vis.top()] = scs;
visited[vis.top()] = 0;
vis.pop();
}
return;
}这里记录的 s i z siz siz 为一个强连通分量的节点数, s c c i scc_i scci 表示节点 i i i 所在强连通分量的编号。 v i s i t e d visited visited 表示某个节点是否在栈内, s c s scs scs 表示现在有多少个强连通分量。
缩点
处理最长路等问题时,如果图不是 DAG,就难以求出结果。所以我们可以用缩点的方法来解决问题。把每个强连通分量看做一个节点,就可以把图变成DAG(证明:有向图的环一定是一个连通分量)。
上面的图缩点后会变成这样:
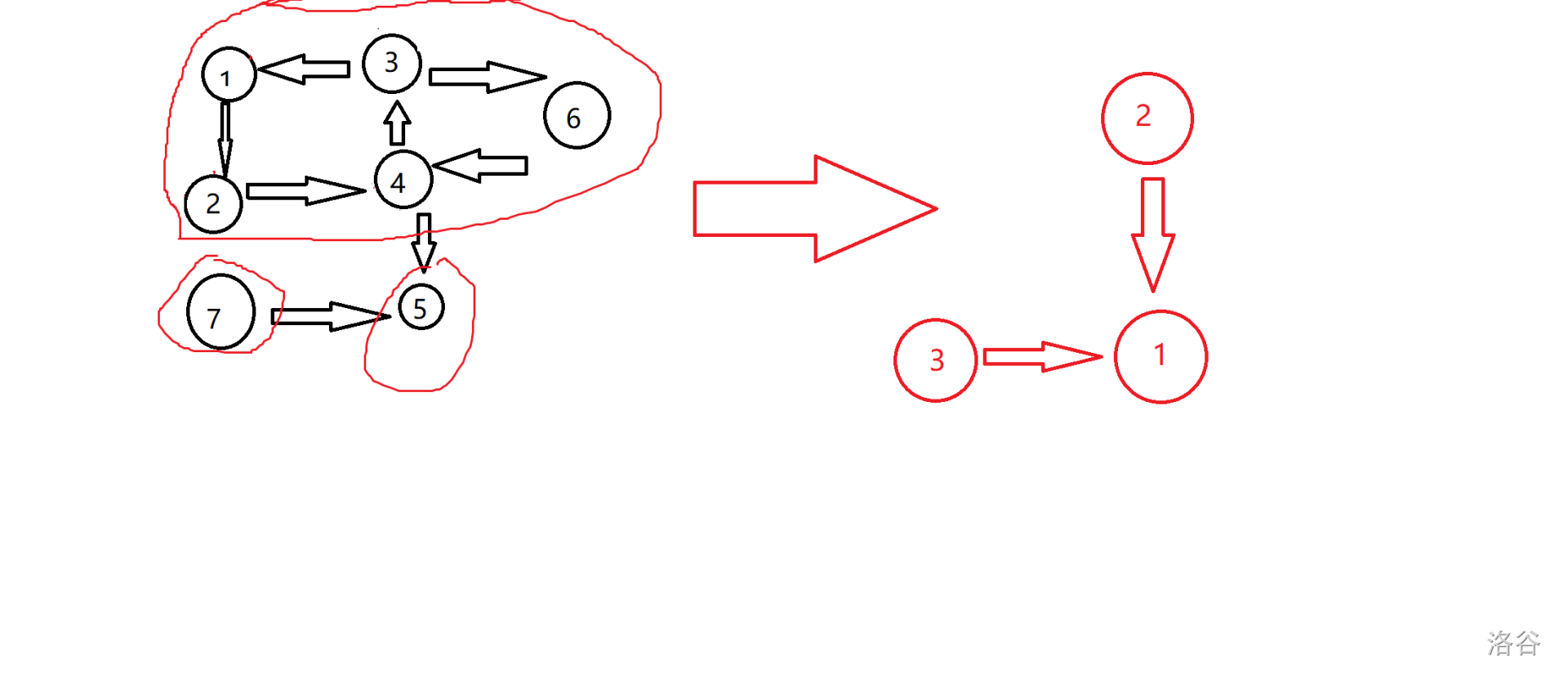
显然,如果一条边连接的两个点在相同的连通分量上时,这条边会被缩掉。反之则不会。比如边 ( 4 , 5 ) (4,5) (4,5) 就没有被缩。
然后注意,如果点有点权,那么新点的点权就是这个连通分量所有点权的和。有边权亦然。
参考代码:
cpp
for(int i = 1;i <= n;i++)
{
for(auto j : pict[i])
{
if(scc[j] != scc[i])
{
dag[scc[i]].push_back(scc[j]);
}
}
}割点和割边
如果删去无向连通图中的一个点或边,图就不再连通,则这个点或边被称为割点、割边(或桥)。例如上图中 4 、 5 4、5 4、5 是割点, ( 4 , 5 ) 、 ( 7 , 5 ) (4,5)、(7,5) (4,5)、(7,5) 是桥。
TARJAN 同样可以很好的判断割点和桥。对于一次 DFS 的根节点,如果有两棵以上的子树(子树之间不连通,没有返祖边),那么它就是割点。
对于非根节点的判断也很简单,对于一条边 ( x , y ) (x,y) (x,y) ,如果 d f n x ≤ l o w y dfn_x \le low_y dfnx≤lowy ,也就是 y y y 不能走到 x x x 的祖先,则 x x x 就是割点。
注意,无向图的 TARJAN 需要额外记录参数 f a t h fath fath 来计算。
到这里,恭喜你学会了TARJAN的基本用法
相关题目
模版题,甚至不用缩点。
cpp
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
int n,m;
int dfn[10004],low[10004],visited[10004],nowdfn = 1,ans;
int scc[10004],siz[10004],scs;
vector <int> pict[10004];
stack <int> vis;
void tarjan(int now)
{
dfn[now] = low[now] = nowdfn++;
vis.push(now);
visited[now] = 1;
for(auto i : pict[now])
{
if(!dfn[i])
{
tarjan(i);
low[now] = min(low[now],low[i]);
}
else if(visited[i]) low[now] = min(low[now],dfn[i]);
}
if(dfn[now] == low[now])
{
scs++;
while(vis.top() != now)
{
siz[scs]++;
scc[vis.top()] = scs;
visited[vis.top()] = 0;
vis.pop();
}
siz[scs]++;
scc[vis.top()] = scs;
visited[vis.top()] = 0;
vis.pop();
if(siz[scs] > 1) ans++;
}
return;
}
int main()
{
cin >> n >> m;
for(int i = 1;i <= m;i++)
{
int a,b;
cin >> a >> b;
pict[a].push_back(b);
}
for(int i = 1;i <= n;i++) if(!dfn[i]) tarjan(i);
cout << ans;
}用 TARJAN 缩点之后,不存在相互爱慕的关系(无环),所以出度唯一为 0 0 0 的强连通分量的所有奶牛是明星。如果有多个强连通分量出度为 0 0 0 则说明没有明星(有其他强连通分量出度为 0 0 0 等于有奶牛没有爱慕我,等于我不是明星)。
cpp
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
int n,m;
int dfn[10004],low[10004],visited[10004],nowdfn = 1;
int scc[10004],siz[10004],scs,dag_in[10004];
vector <int> pict[10004];
vector <int> dag[10004];
stack <int> vis;
void tarjan(int now)
{
dfn[now] = low[now] = nowdfn++;
vis.push(now);
visited[now] = 1;
for(auto i : pict[now])
{
if(!dfn[i])
{
tarjan(i);
low[now] = min(low[now],low[i]);
}
else if(visited[i]) low[now] = min(low[now],dfn[i]);
}
if(dfn[now] == low[now])
{
scs++;
while(vis.top() != now)
{
siz[scs]++;
scc[vis.top()] = scs;
visited[vis.top()] = 0;
vis.pop();
}
siz[scs]++;
scc[vis.top()] = scs;
visited[vis.top()] = 0;
vis.pop();
}
return;
}
int main()
{
cin >> n >> m;
for(int i = 1;i <= m;i++)
{
int a,b;
cin >> a >> b;
pict[a].push_back(b);
}
for(int i = 1;i <= n;i++) if(!dfn[i]) tarjan(i);
for(int i = 1;i <= n;i++)
{
for(auto j : pict[i])
{
if(scc[j] != scc[i])
{
dag[scc[i]].push_back(scc[j]);
dag_in[scc[i]]++;
}
}
}
int flag = 0;
for(int i = 1;i <= scs;i++)
{
if(!dag_in[i] && flag)
{
flag = 0;
break;
}
if(!dag_in[i]) flag = i;
}
if(flag) cout << siz[flag];
else cout << 0;
}[IOI 1996 / USACO5.3] Network of Schools
先用 TARJAN 缩点。
问题 1 1 1 很简单,缩点之后入度为 0 0 0 的点必须下发一份软件,因为他们不能从其他连通块获得软件。
问题 2 2 2 要稍微复杂一点。很显然我们要把缩点后的图变成强连通图,而强连通图每个点的入度和出度至少为 1 1 1 。因此我们把出度为 0 0 0 的点连到入度为 0 0 0 的点上,扩展次数为两种节点数量的最大值。注意特判只有 1 1 1 个强连通分量的情况。
cpp
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
int n,ans,ans2;
vector <int> pict[102];
int dfn[102],low[102],nowdfn;
int loc[102],siz[102],id;
int insum[102],outsum[102];
bool visited[102];
stack <int> init;
void dfs(int now)
{
init.push(now);
visited[now] = 1;
dfn[now] = low[now] = ++nowdfn;
for(auto i : pict[now])
{
if(!dfn[i])
{
dfs(i);
low[now] = min(low[now],low[i]);
}
else if(visited[i]) low[now] = min(low[now],dfn[i]);
}
if(dfn[now] == low[now])
{
id++;
while(init.top() != now)
{
loc[init.top()] = id;
siz[id]++;
visited[init.top()] = 0;
init.pop();
}
visited[init.top()] = 0;
loc[init.top()] = id;
siz[id]++;
init.pop();
}
}
int main()
{
cin >> n;
for(int i = 1;i <= n;i++)
{
int x;
while(cin >> x)
{
if(!x) break;
pict[i].push_back(x);
}
}
for(int i = 1;i <= n;i++) if(!dfn[i]) dfs(i);
for(int i = 1;i <= n;i++)
{
for(auto j : pict[i])
{
if(loc[i] != loc[j])
{
insum[loc[j]]++;
outsum[loc[i]]++;
}
}
}
for(int i = 1;i <= id;i++)
{
if(!insum[i]) ans++;
if(!outsum[i]) ans2++;
}
cout << ans << '\n';
if(id == 1) cout << 0;
else cout << max(ans2,ans);
}fun fact:此代码改一下数组范围可通过加强版
先遍历所有间谍。如果一个间谍可以被购买且未被访问过就用它做一次 Tarjan,控制每个强连通分量的成本为这个强连通分量价格最低的间谍。之后没访问过的间谍控制不了。如果可以控制所有间谍,容易知道应当购买入度为 0 0 0 的间谍。
cpp
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
int n,r,p;
int buy[3003];
vector <int> pict[3003];
int dfn[3003],low[3003],nowdfn = 1,buyscc[3003];
bool instack[3003];
int scc[3003],scs,ans;
int insum[3003];
stack <int> nowblock;
void tarjan(int now)
{
dfn[now] = low[now] = nowdfn++;
nowblock.push(now);
instack[now] = 1;
for(auto i : pict[now])
{
if(!dfn[i])
{
tarjan(i);
low[now] = min(low[now],low[i]);
}
else if(instack[i]) low[now] = min(low[now],dfn[i]);
}
if(dfn[now] == low[now])
{
scs++;
buyscc[scs] = -1;
while(nowblock.top() != now)
{
scc[nowblock.top()] = scs;
if(buy[nowblock.top()] != -1)
{
if(buyscc[scs] == -1) buyscc[scs] = buy[nowblock.top()];
else buyscc[scs] = min(buyscc[scs],buy[nowblock.top()]);
}
instack[nowblock.top()] = 0;
nowblock.pop();
}
if(buy[nowblock.top()] != -1)
{
if(buyscc[scs] == -1) buyscc[scs] = buy[nowblock.top()];
else buyscc[scs] = min(buyscc[scs],buy[nowblock.top()]);
}
scc[nowblock.top()] = scs;
instack[nowblock.top()] = 0;
nowblock.pop();
}
}
int main()
{
cin >> n >> p;
for(int i = 1;i <= n;i++) buy[i] = -1;
for(int i = 1;i <= p;i++)
{
int a,b;
cin >> a >> b;
buy[a] = b;
}
cin >> r;
for(int i = 1;i <= r;i++)
{
int a,b;
cin >> a >> b;
pict[a].push_back(b);
}
for(int i = 1;i <= n;i++) if(!dfn[i] && buy[i] != -1) tarjan(i);
for(int i = 1;i <= n;i++)
{
if(!dfn[i])
{
cout << "NO\n" << i;
return 0;
}
}
cout << "YES\n";
for(int i = 1;i <= n;i++)
{
for(auto j : pict[i])
{
if(scc[i] != scc[j]) insum[scc[j]]++;
}
}
for(int i = 1;i <= scs;i++)
{
if(!insum[i]) ans += buyscc[i];
}
cout << ans;
}[USACO15JAN] Grass Cownoisseur G
更多好题可在洛谷搜索标签Tarjan和强连通分量 。