TL;DR
- 场景:如何快速判断一个网络是否"一笔画/欧拉回路"?
- 结论:给无向/有向判定条件 + 可运行脚本,一次性搞定。
- 产出:euler_checker.py、判定速查卡

图论
图论起源
柯尼斯堡(Königsberg)七桥问题是图论发展史上的里程碑事件。18世纪初,这座位于普鲁士(现俄罗斯加里宁格勒)的城市被普雷格尔河(Pregel River)分成四个主要区域,并由七座桥连接:
- 克奈普霍夫桥(Knäpperbrücke)
- 格林桥(Grüne Brücke)
- 商铺桥(Krämerbrücke)
- 铁匠桥(Schmiedebrücke)
- 蜂蜜桥(Honigbrücke)
- 高桥(Hohe Brücke)
- 木桥(Holzbrücke)
当时城中流传着一个趣题:能否设计一条路线,使得一个人可以恰好走过每座桥一次并返回起点?这个问题引起了数学家们的广泛兴趣。
1735年,瑞士著名数学家莱昂哈德·欧拉(Leonhard Euler)开始研究这个问题。经过深入思考,他于1736年8月26日在给意大利数学家乔瓦尼·马里诺尼(Giovanni Marinoni)的信中首次给出了解答。随后在1738年,欧拉在圣彼得堡科学院发表论文《柯尼斯堡七桥问题解》(Solutio problematis ad geometriam situs pertinentis),正式证明了这样的路径不存在。
欧拉的解决方案创造性地将实际问题抽象为数学图形:
- 将四个城区表示为顶点
- 将七座桥表示为边
- 将问题转化为寻找图中的欧拉回路
这一开创性工作奠定了图论的基础,欧拉也因此被公认为图论之父。他的这一贡献不仅解决了一个具体问题,更重要的是开创了一个全新的数学分支,为后世研究网络结构、路径规划等问题提供了理论基础。今天,这种不重复经过边的回路被称为"欧拉回路",存在欧拉回路的图则称为"欧拉图"。
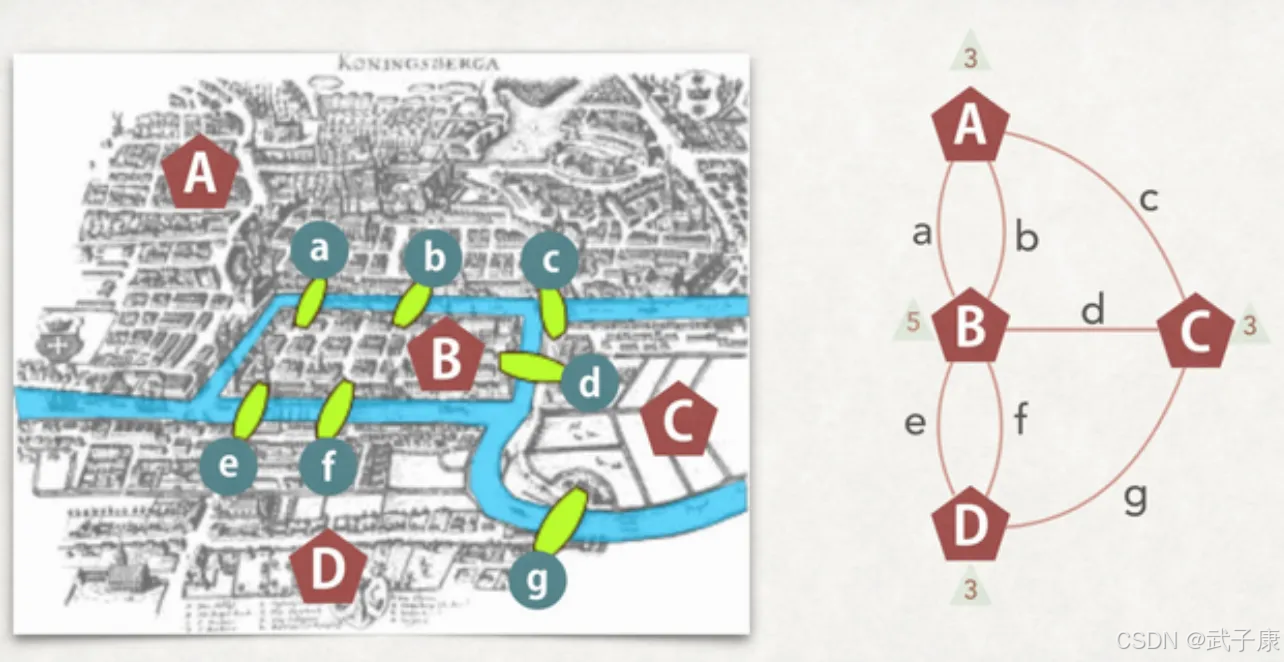
欧拉通过对柯尼斯堡七桥问题的深入研究,将这类路径问题的本质归纳为"一笔画"问题。这个数学概念在当代被称为"欧拉路径"或"欧拉回路",其核心是要判断一个给定的图(graph)能否通过一条连续的路径遍历所有的边(Edge)而不出现重复经过的情况。柯尼斯堡七桥问题实际上是"一笔画"问题的一个具体实例,它要求寻找一条能够经过所有七座桥各一次的路线。
欧拉通过严密的数学论证,证明了柯尼斯堡七桥问题不存在这样的解决方案。在1736年发表的论文中,他建立了"一笔画"问题的两个决定性条件:
-
图的连通性条件:
- 图必须是一个连通图(Connected Graph),即图中任意两个顶点(Vertex)之间都存在路径相连
- 对于欧拉回路(起点和终点相同的路径),图中所有顶点的度数(连接的边数)必须都是偶数
- 对于欧拉路径(起点和终点不同的路径),图中必须恰好有两个顶点的度数是奇数,其余都是偶数
-
具体应用示例:
- 以柯尼斯堡七桥为例,四个陆地区域对应的顶点度数分别为3、3、3和5,都是奇数,因此不满足条件
- 与此形成对比的是,一个简单的四边形图,每个顶点度数为2(偶数),就存在欧拉回路
- 一个"日"字形图,两个端点度数为1(奇数),中间点度数为2(偶数),就存在欧拉路径
欧拉的这一发现开创了图论研究的先河,为后来的网络分析、电路设计等领域奠定了基础。在实际应用中,这些原理可以用于:
- 设计高效的物流配送路线
- 规划城市交通信号系统
- 优化计算机网络的数据传输路径
- 解决各种迷宫和益智游戏问题
图和节点
图是由一组节点(也称顶点)和连接这些节点的边(也称关系)组成的非线性数据结构。图形数据主要通过节点和边上的属性进行存储和表示,这些属性以键值对(Key-Value Pair)的形式存在。
在图形理论的可视化表示中:
-
节点通常用圆形(或椭圆形)表示,每个节点可以包含:
- 一个唯一标识符(如ID)
- 多个属性键值对(如"name":"张三","age":25)
- 可选的类型标签(如"Person"、"Product")
-
边表示节点之间的关系,具有:
- 方向性(有向边或无向边)
- 一个或多个关系类型(如"KNOWS"、"PURCHASED")
- 自身的属性键值对(如"since":2020,"amount":100)
应用示例:
- 社交网络:节点表示用户(属性包括姓名、年龄等),边表示好友关系(属性包括成为好友的时间)
- 推荐系统:产品节点通过"购买"边连接用户节点,边属性可包含购买时间和评分
- 知识图谱:实体作为节点,关系作为边,共同构成语义网络
在图形数据库(如Neo4j)中,这种表示方式允许高效的图遍历和复杂关系查询,特别适合处理多跳关系和网络分析场景。
节点关系
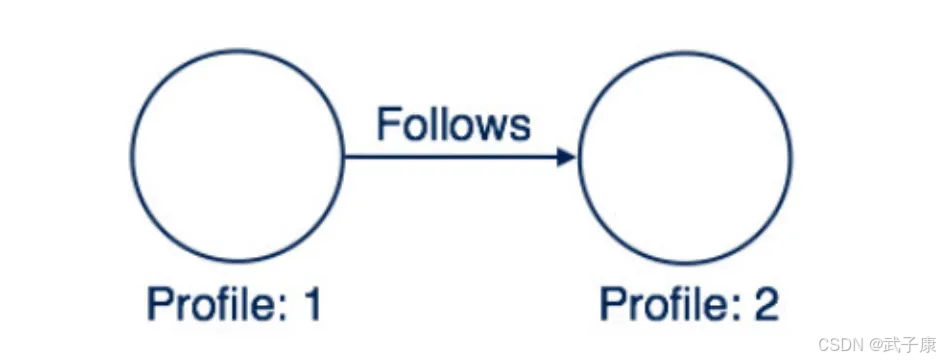
简单关系表达
此处两个节点之间的创建的关系名称为"追随",这意味着 Profile1 和 Prolfile2.
复杂关系表达
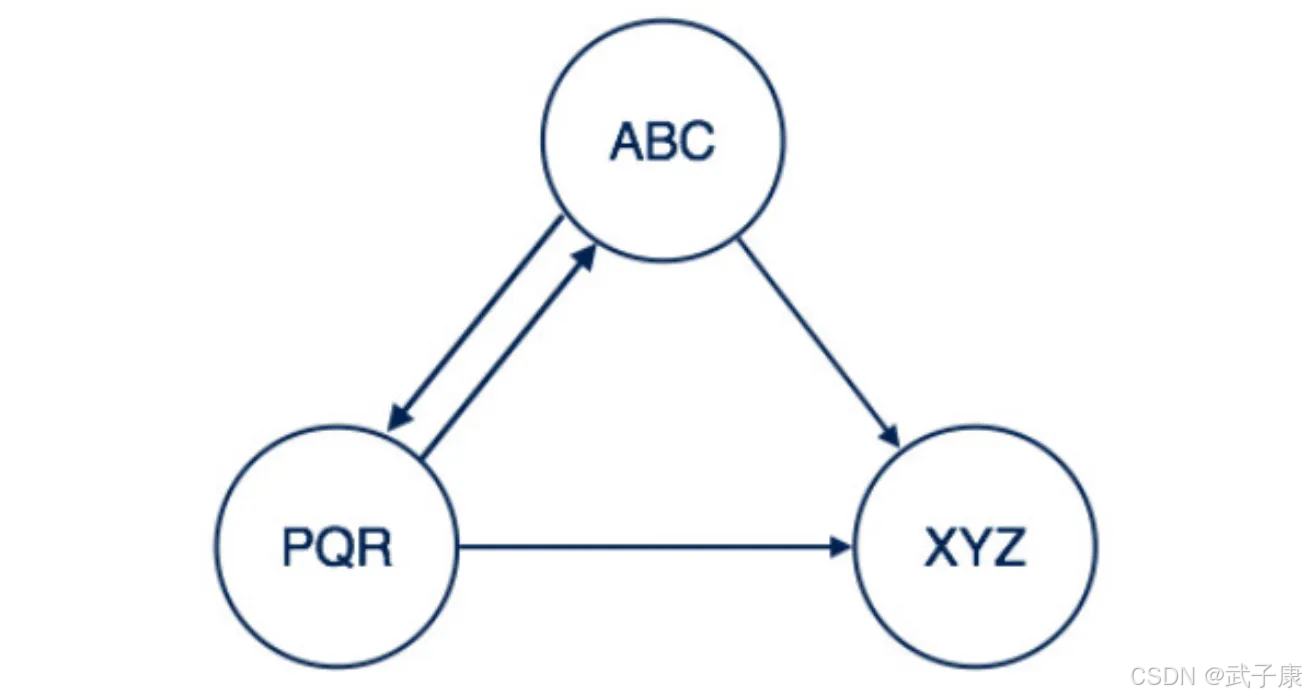
这里节点用关系连接,关系是单向或双向的:
● 从 XYZ 到 PQR 的关系是单向关系
● 从 ABC 到 XYZ 的关系是双向关系
属性图模型规则
● 图表示节点,关系和属性中的数据
● 节点和关系都包含属性
● 关系连接节点
● 属性是键值对
● 节点用圆圈表示,关系用方向键表示
● 关系具有方向:单向和双向
● 每个关系包含:开始节点、从节点、到节点、结束节点
图谱与图库
知识图谱
基于图的知识图谱数据结构
知识图谱本质上是一种基于图结构的数据组织形式,由两个核心要素构成:
-
节点(Node):代表知识体系中的实体(Entity),每个节点具有以下特征:
- 具有全局唯一的标识符(ID)
- 可以表示人、地点、事物、概念等多种类型的实体
- 例如:在人物知识图谱中,"爱因斯坦"可以作为一个节点,用唯一ID"Q937"标识
-
边(Edge):代表实体之间的关系(Relationship),其特征包括:
- 连接两个节点,表示它们之间的特定关联
- 可以带有类型和属性信息
- 例如:"爱因斯坦"节点与"相对论"节点之间可以用"提出"关系的边连接
知识图谱的典型特征
知识图谱构建了一个异构信息网络,具有以下显著特点:
-
信息整合能力:
- 能够融合来自不同来源、不同格式的数据
- 例如整合结构化的数据库和非结构化的网页文本
-
关系网络特性:
- 形成实体间的复杂关系网络
- 支持多跳查询(如查询"爱因斯坦的老师的国籍")
-
推理分析能力:
- 通过关系路径发现隐含知识
- 支持基于图算法的关联分析
知识图谱在搜索引擎中的应用
在互联网大数据时代,主要搜索引擎都构建了自己的知识图谱系统:
-
Google Knowledge Graph:
- 2012年正式推出
- 包含超过500亿个事实数据
- 在搜索结果右侧显示知识卡片
-
百度知心:
- 中文领域最大的知识图谱
- 覆盖人物、地点、机构等实体类型
- 支持智能问答和关联推荐
-
搜狗知立方:
- 专注于中文搜索优化
- 整合医疗、教育等垂直领域知识
- 提供精准的实体识别和关系抽取
这些知识图谱系统显著提升了搜索质量:
- 从关键词匹配升级到语义理解
- 提供结构化答案而非简单网页链接
- 实现关联知识的智能推荐
- 支持复杂查询的推理回答
实际应用示例:当用户搜索"特斯拉CEO"时,搜索引擎不仅能返回马斯克的基本信息,还能展示其相关公司、教育背景等关联实体,形成完整的知识网络。
图数据库
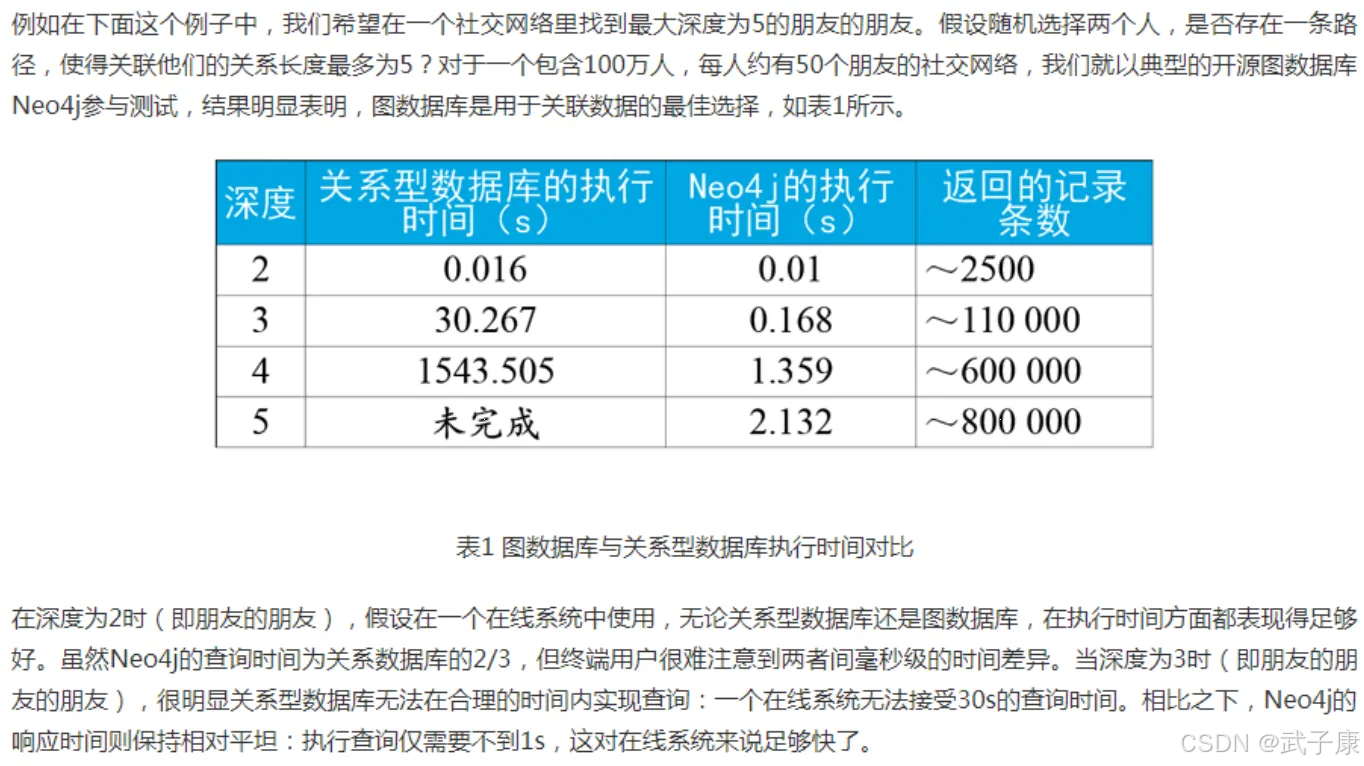
一般情况下,我们使用数据库查找事物间的联系的时候,只需要短程关系的查询(两层以内的关联)。当需要进行更长程的,更广范围的关系查询时,就需要图数据库的功能。
而随着社交、电商、金融、零售、物联网等行业的快速发展,现实世界的事物之间织齐了一张巨大复杂的关系网,传统数据库面对这样复杂的关系往往束手无策。因此,有了图数据库。
图数据库优势
在需要表示多对多的关系时,传统的处理方式通常会遇到复杂度提升的问题。以学生选课系统为例,在关系型数据库中,我们需要创建一个名为"学生课程关联表"的中间表来记录学生和课程之间的多对多关系。如果这两个实体之间还存在其他关系,比如"学生担任课程助教"的关系,就需要额外再创建一个"学生课程助教关联表"。这种处理方式会导致数据库中出现大量关联表,增加了系统复杂度。
而在图形数据库中,这种多对多关系的表示就变得直观且灵活。例如,在Neo4j这样的图形数据库中,我们可以直接在学生节点和课程节点之间建立两种不同的关系:一种是"选修"关系,另一种是"担任助教"关系。每种关系都可以携带各自的属性,"选修"关系可以包含"选课时间"和"成绩"等属性,而"担任助教"关系则可以记录"担任时间"和"负责内容"等信息。
当需要建立双向关系时,图形数据库的处理方式也十分清晰。以社交网络中的"关注"关系为例,如果我们想要表示"A关注B"和"B关注A"这两个不同的关系,只需分别建立两个方向的关系边即可。在关系型数据库中,这通常需要在关联表中通过额外的字段来区分方向,或者创建两张不同的关联表。
图形数据库的关系属性功能为用户提供了更灵活的数据建模方式。例如,在供应链管理系统中,两个公司节点之间的"供应"关系可以包含"供应量"、"供应周期"、"合同条款"等丰富属性,而不需要像关系型数据库那样将这些信息分散存储在不同的表中。这种特性使得图形数据库特别适合表示现实世界中复杂的网络关系,如社交网络、推荐系统、知识图谱等场景。
因此,相对于关系型数据库中需要通过各种关联表来表示实体间关系的局限性,图形数据库通过其灵活的关系表示能力,为用户提供了一种更自然、更强大的数据建模工具。这使得开发者在面对复杂的网络关系时,能够更直观地对现实世界进行抽象和建模。
优势总结:
● 性能上,对长程关系的查询速度快
● 擅长发现隐藏的关系,例如通过判断上两点之间有没有走的通的路径,就可以发现事务间的关联。
最小可运行示例
shell
# 环境准备(本地或容器均可)
pip install networkx
# 运行演示(内置:柯尼斯堡、四边形、有向三环等)
python euler_checker.py也可以这么写:
shell
# 无向:A-B 表示一条边
python euler_checker.py --undirected "A-B,B-C,C-D,D-A"
# 有向:A->B 表示一条有向边
python euler_checker.py --directed "A->B,B->C,C->A"
python
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
euler_checker.py
快速判断图是否存在欧拉路径/欧拉回路(无向/有向)
依赖:pip install networkx
用法:
1) 直接运行,查看内置示例:
python euler_checker.py
2) 从命令行输入边(简单解析):
# 无向图:用 A-B 表示一条边,逗号分隔
python euler_checker.py --undirected "A-B,B-C,C-D,D-A"
# 有向图:用 A->B 表示一条边,逗号分隔
python euler_checker.py --directed "A->B,B->C,C->A"
3) 从文件读取:一行一条边
无向:A B
有向:A B (配合 --directed)
python euler_checker.py --file edges.txt
"""
import argparse
import sys
from typing import List, Tuple
import networkx as nx
def parse_edges(text: str, directed: bool) -> List[Tuple[str, str]]:
edges: List[Tuple[str, str]] = []
text = text.strip()
if not text:
return edges
parts = [p.strip() for p in text.split(',') if p.strip()]
for p in parts:
if directed:
if '->' not in p:
raise ValueError(f"有向边应使用 A->B 格式,但收到:{p}")
a, b = [x.strip() for x in p.split('->', 1)]
else:
if '-' not in p:
raise ValueError(f"无向边应使用 A-B 格式,但收到:{p}")
a, b = [x.strip() for x in p.split('-', 1)]
edges.append((a, b))
return edges
def load_edges_from_file(path: str) -> List[Tuple[str, str]]:
edges: List[Tuple[str, str]] = []
with open(path, 'r', encoding='utf-8') as f:
for line in f:
line = line.strip()
if not line or line.startswith('#'):
continue
cols = line.split()
if len(cols) >= 2:
edges.append((cols[0], cols[1]))
return edges
def euler_undirected_report(G: nx.Graph) -> str:
# 仅考虑度数>0的连通分量
non_isolated = [n for n, d in G.degree() if d > 0]
if non_isolated:
H = G.subgraph(non_isolated)
connected = nx.is_connected(H)
else:
connected = True # 无边图视作连通用于欧拉回路定义的边界情形
odd_nodes = [n for n, d in G.degree() if d % 2 == 1]
has_euler_circuit = connected and len(odd_nodes) == 0
has_euler_path = connected and (len(odd_nodes) == 0 or len(odd_nodes) == 2)
lines = []
lines.append("【无向图 欧拉判定】")
lines.append(f"- 连通(忽略孤立点):{connected}")
lines.append(f"- 奇度顶点个数:{len(odd_nodes)} ;节点:{odd_nodes}")
lines.append(f"- 是否存在欧拉回路:{has_euler_circuit}")
lines.append(f"- 是否存在欧拉路径:{has_euler_path}")
return "\n".join(lines)
def euler_directed_report(G: nx.DiGraph) -> str:
# 仅考虑入度+出度>0的节点诱导子图
non_isolated = [n for n in G.nodes() if (G.in_degree(n) + G.out_degree(n)) > 0]
H = G.subgraph(non_isolated).copy()
# 弱连通判断(忽略方向)
connected = True
if non_isolated:
UG = H.to_undirected()
connected = nx.is_connected(UG)
in_eq_out = [n for n in H.nodes() if G.in_degree(n) == G.out_degree(n)]
plus1 = [n for n in H.nodes() if G.out_degree(n) == G.in_degree(n) + 1]
minus1 = [n for n in H.nodes() if G.in_degree(n) == G.out_degree(n) + 1]
has_euler_circuit = connected and len(in_eq_out) == len(H.nodes())
has_euler_path = connected and (len(plus1) == 1 and len(minus1) == 1 and
len(in_eq_out) == len(H.nodes()) - 2)
lines = []
lines.append("【有向图 欧拉判定】")
lines.append(f"- 弱连通(忽略方向):{connected}")
lines.append(f"- 入度=出度 节点数:{len(in_eq_out)}")
lines.append(f"- out=in+1 节点:{plus1}")
lines.append(f"- in=out+1 节点:{minus1}")
lines.append(f"- 是否存在欧拉回路:{has_euler_circuit}")
lines.append(f"- 是否存在欧拉路径:{has_euler_path}")
return "\n".join(lines)
def demo():
print("== 无向图示例 ==")
# 柯尼斯堡七桥(抽象化示例,边多重在简单图中折算为度数)
G = nx.MultiGraph()
# 四个陆地区域 A,B,C,D;七座桥连接(多重边)
edges_multi = [
("A", "B"),
("A", "B"),
("A", "C"),
("A", "D"),
("B", "C"),
("B", "D"),
("C", "D"),
]
G.add_edges_from(edges_multi)
# 转为简单图做度数奇偶与连通判定(保留度数信息用 MultiGraph.degree 即可)
# 这里我们直接用MultiGraph的度数奇偶性
odd_nodes = [n for n, d in G.degree() if d % 2 == 1]
UG = nx.Graph()
UG.add_nodes_from(G.nodes())
UG.add_edges_from(G.edges())
print(euler_undirected_report(UG))
print()
print("== 无向图示例(有欧拉回路) ==")
H = nx.Graph()
H.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A")]) # 四边形
print(euler_undirected_report(H))
print()
print("== 无向图示例(有欧拉路径) ==")
I = nx.Graph()
I.add_path(["A", "B", "C"]) # "日"字形简化为一条链
print(euler_undirected_report(I))
print()
print("== 有向图示例 ==")
D = nx.DiGraph()
D.add_edges_from([("A","B"),("B","C"),("C","A")])
print(euler_directed_report(D))
print()
def main():
parser = argparse.ArgumentParser(description="欧拉路径/回路判定(无向/有向)")
group = parser.add_mutually_exclusive_group()
group.add_argument("--undirected", type=str, help="无向边列表,如 "A-B,B-C,C-D"")
group.add_argument("--directed", type=str, help="有向边列表,如 "A->B,B->C"")
parser.add_argument("--file", type=str, help="从文件读取边,每行两个节点(A B)")
parser.add_argument("--digraph", action="store_true", help="配合 --file,将输入视为有向图")
args = parser.parse_args()
if args.undirected:
edges = parse_edges(args.undirected, directed=False)
G = nx.Graph()
G.add_edges_from(edges)
print(euler_undirected_report(G))
return
if args.directed:
edges = parse_edges(args.directed, directed=True)
D = nx.DiGraph()
D.add_edges_from(edges)
print(euler_directed_report(D))
return
if args.file:
edges = load_edges_from_file(args.file)
if args.digraph:
D = nx.DiGraph()
D.add_edges_from(edges)
print(euler_directed_report(D))
else:
G = nx.Graph()
G.add_edges_from(edges)
print(euler_undirected_report(G))
return
# 没有参数则跑演示
demo()
if __name__ == "__main__":
main()其他系列
🚀 AI篇持续更新中(长期更新)
AI炼丹日志-29 - 字节跳动 DeerFlow 深度研究框斜体样式架 私有部署 测试上手 架构研究 ,持续打造实用AI工具指南!
AI-调查研究-108-具身智能 机器人模型训练全流程详解:从预训练到强化学习与人类反馈
🔗 AI模块直达链接
💻 Java篇持续更新中(长期更新)
Java-154 深入浅出 MongoDB 用Java访问 MongoDB 数据库 从环境搭建到CRUD完整示例
MyBatis 已完结,Spring 已完结,Nginx已完结,Tomcat已完结,分布式服务正在更新!深入浅出助你打牢基础!
🔗 Java模块直达链接
📊 大数据板块已完成多项干货更新(300篇):
包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件,覆盖离线+实时数仓全栈!
大数据-278 Spark MLib - 基础介绍 机器学习算法 梯度提升树 GBDT案例 详解
🔗 大数据模块直达链接