本文是记录专业课"计算机图形学"的部分笔记,参考教材为Angel的第八版交互式计算机图形学------基于WebGL 2.0的自顶向下方法。
1、在OpenGL中,二维是三维的一个特例,而三维其实变化不大,使用 glVertex3*( )即可。需要考虑的是多边形的绘制顺序、使用隐藏面消除技术以及简单性、凸性和平面性。
2、让我们先考虑二维的The Sierpinski Gasket(谢尔宾斯基垫):
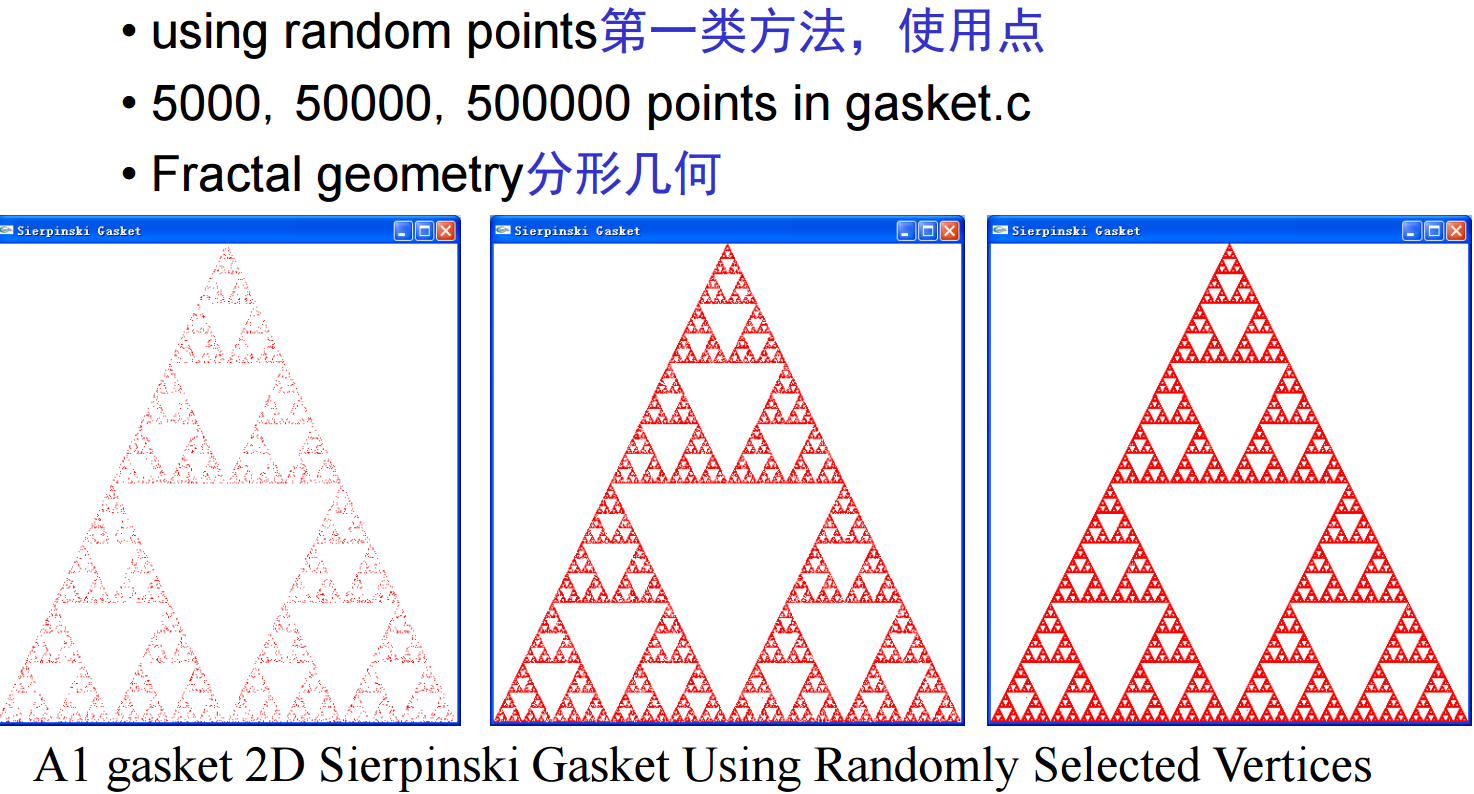
算法如下图,核心是利用随机过程和迭代函数系统。具体流程是①在三角形内部任意选择一个初始点 p0;②从三角形的三个顶点中随机选择一个;③找到当前点 p与上一步选中的顶点之间的中点q并绘制;④将当前点 p的位置更新为刚刚计算出的中点 q的位置(即 pn+1=qn),为下一次迭代做准备;⑤跳回第二步。

上述算法是A1 gasket 2D Sierpinski Gasket Using Randomly Selected Vertices,而对于A2 Sierpinski Gasket 2D ,先从一个三角形开始,连接三边的中点并去掉中间的三角形,再重复上述过程。对于A2的分形效果,我们考虑填充区域(黑色)和周长(围绕填充三角形的所有线的长度):随着我们继续细分,面积变为零但周长趋于无穷大,这不是一个普通的几何对象(既不是二维也不是三维)、而是一个分形(分形维数)对象(例如英格兰海岸线为1.02维)。
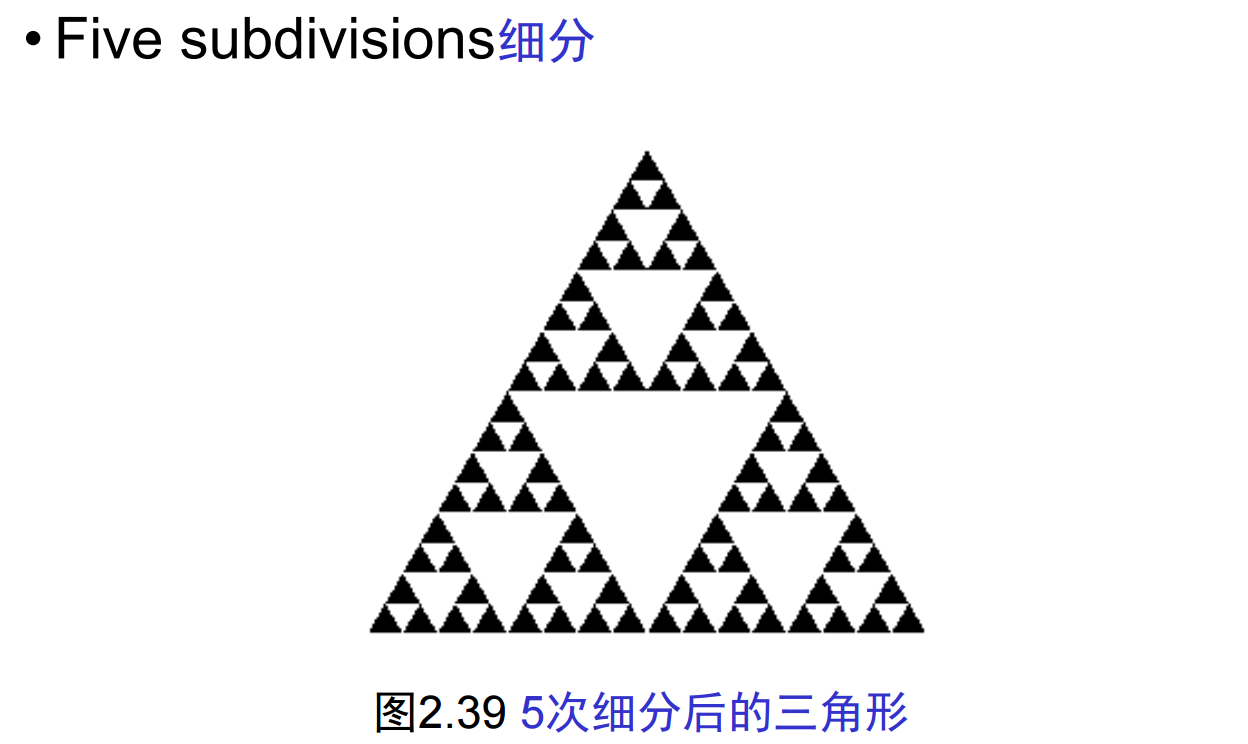
A2 Sierpinski Gasket 2D 示例程序:
#include <GL/glut.h>
/* initial triangle */
GLfloat v[3][2]={{-1.0, -0.58}, {1.0, -0.58}, {0.0, 1.15}};
/* number of recursive steps递归次数*/
int n; // 全局变量 递归层次
//绘制三角形:
void triangle( GLfloat *a, GLfloat *b, GLfloat *c)
/* display one triangle */
{
glVertex2fv(a);
glVertex2fv(b);
glVertex2fv(c);
}
//三角形细分:
void divide_triangle(GLfloat *a, GLfloat *b, GLfloat *c, int m)
{
/* triangle subdivision using vertex numbers */
point2 v0, v1, v2;
int j;
if(m>0) {
for(j=0; j<2; j++) v0[j]=(a[j]+b[j])/2;
for(j=0; j<2; j++) v1[j]=(a[j]+c[j])/2;
for(j=0; j<2; j++) v2[j]=(b[j]+c[j])/2;
divide_triangle(a, v0, v1, m-1);
divide_triangle(c, v1, v2, m-1);
divide_triangle(b, v2, v0, m-1);
}
else
triangle(a,b,c);
/* draw triangle at end of recursion */
}
//显示与初始化函数:
void display()
{
glClear(GL_COLOR_BUFFER_BIT);
glBegin(GL_TRIANGLES);
divide_triangle(v[0], v[1], v[2], n); // 全局参变量 n
glEnd();
glFlush();
}
void myinit()
{
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(-2.0, 2.0, -2.0, 2.0);
glMatrixMode(GL_MODELVIEW);
glClearColor (1.0, 1.0, 1.0,1.0); //背景白色,屏幕
glColor3f(0.0,0.0,0.0); //前景黑色,三角形
}
//主函数:
int main(int argc, char **argv)
{
n=4; //程序指定,还可以用户输入,交互界面 或者 命令行
glutInit(&argc, argv); // 初始化GLUT
glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);
glutInitWindowSize(500, 500);
glutCreateWindow("2D Gasket");
glutDisplayFunc(display);
myinit();
glutMainLoop();
}通过将glBegin和glEnd放在显示回调中而不是在triangle函数中,并在glBegin中使用GL_TRIANGLES而不是GL_POLYGON,我们只需为整个垫片调用一次glBegin和glEnd,而不是为所有三角形都调用一次。不过也可以用glDrawArrays(GL_TRIANGLES, 0, Nvertices);
3、而对于三维垫,可以使用三维点(GLfloat v[3][3]、glVertex3f、glOrtho)的方式,但不好。因此我们采用四面体(tetrahedron)方法。

//三角形代码:
void triangle( GLfloat *a, GLfloat *b,
GLfloat *c)
{
glVertex3fv(a);
glVertex3fv(b);
glVertex3fv(c);
}
void divide_triangle(GLfloat *a, GLfloat *b, GLfloat *c, int m)
{
GLfloat v1[3], v2[3], v3[3];
int j;
if(m>0)
{
for(j=0; j<3; j++) v1[j]=(a[j]+b[j])/2;
for(j=0; j<3; j++) v2[j]=(a[j]+c[j])/2;
for(j=0; j<3; j++) v3[j]=(b[j]+c[j])/2;
divide_triangle(a, v1, v2, m-1);
divide_triangle(c, v2, v3, m-1);
divide_triangle(b, v3, v1, m-1);
}
else(triangle(a,b,c));
}
//生成四面体:
void tetrahedron(int m)
{
glColor3f(1.0,0.0,0.0);
divide_triangle(v[0], v[1], v[2], m);
glColor3f(0.0,1.0,0.0);
divide_triangle(v[3], v[2], v[1], m);
glColor3f(0.0,0.0,1.0);
divide_triangle(v[0], v[3], v[1], m);
glColor3f(0.0,0.0,0.0);
divide_triangle(v[0], v[2], v[3], m);
}4、不过在三维中,由于三角形是按照程序中的定义顺序绘制的,因此前面的三角形并不总是渲染在它们后面的三角形前面,这涉及了遮挡/消隐问题:
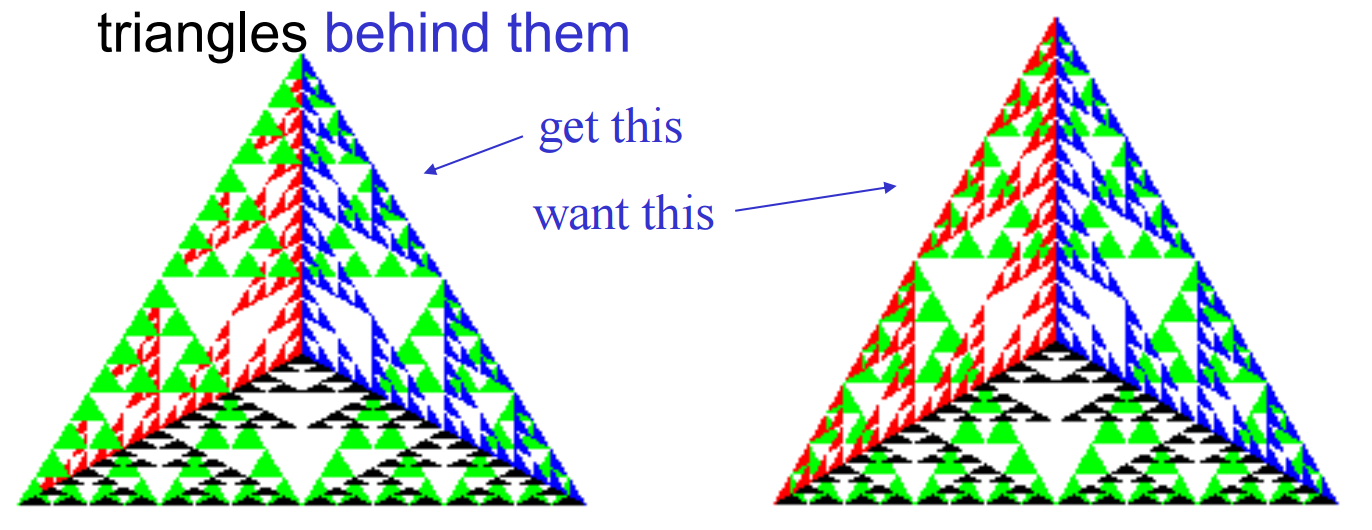
我们只想看到位于其他表面之前的那些表面,OpenGL采用z缓冲算法,使用了一个硬件支持的额外缓冲区,在渲染对象时保存深度信息,以便图像中只显示前面的对象。使用时需要①在main.c中给绘制模式加上z缓冲区 glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);②在init.c中启动深度测试状态 glEnable(GL_DEPTH_TEST);③清屏时候同时清理深度缓存glClear(GL_COLOR_BUFFER_BIT | //当前可写的颜色缓存 GL_DEPTH_BUFFER_BIT)//将所有像素的深度值设置为最大可能距离(一般是远剪裁面)。
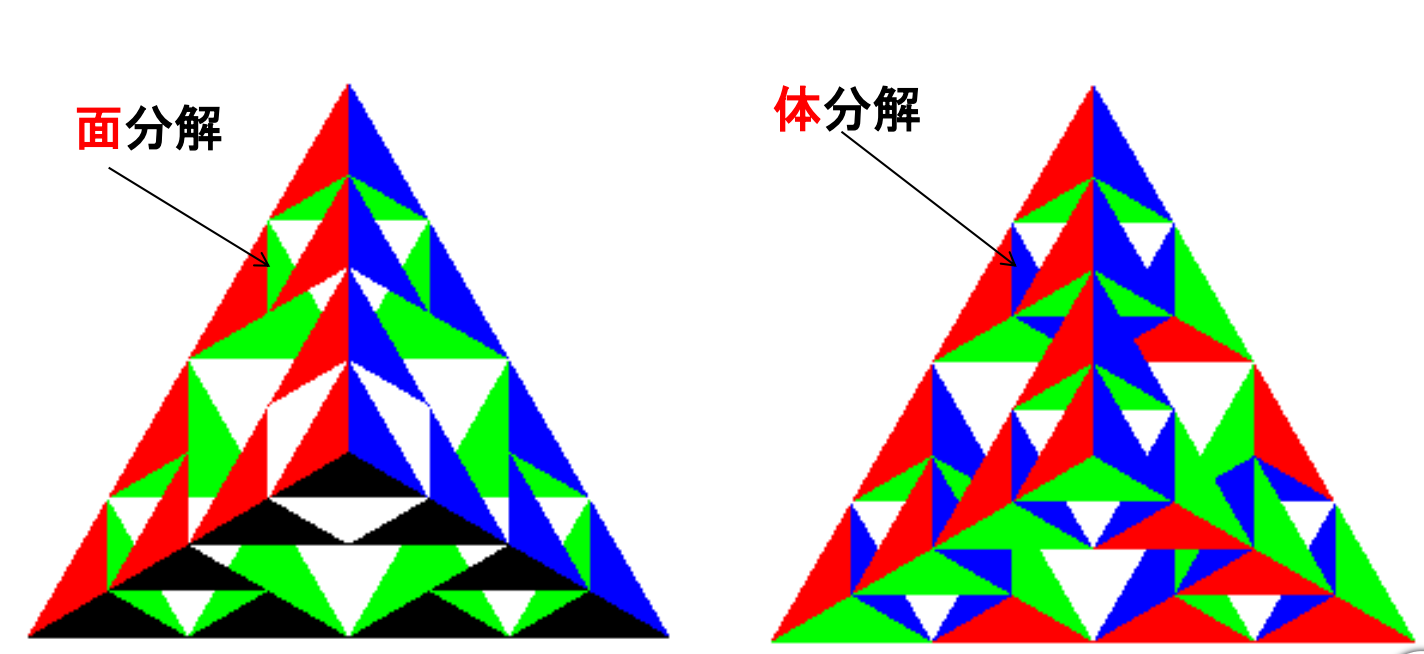
5、另外,在上述示例中,我们对每个物体进行了面分解,实际上体分解也是可以的: