文章目录
- 前文链接
- 一、乘法逆元
-
- [1. 定义](#1. 定义)
- [2. 逆元存在的条件](#2. 逆元存在的条件)
- [3. 逆元的应用](#3. 逆元的应用)
- 二、求逆元的方法
-
- [1. 费马小定理 + 快速幂](#1. 费马小定理 + 快速幂)
- [2. 扩展欧几里得算法(exgcd)](#2. 扩展欧几里得算法(exgcd))
- [3. 递推法](#3. 递推法)
- 三、练习
-
- [1. 序列求和 ⭐⭐](#1. 序列求和 ⭐⭐)
- [2.【模板】逆元 ⭐⭐](#2.【模板】逆元 ⭐⭐)
- [3.【模板】模意义下的乘法逆元 ⭐⭐](#3.【模板】模意义下的乘法逆元 ⭐⭐)
前文链接
一、乘法逆元
1. 定义
对于正整数 a a a 和 p p p,若有
a x ≡ 1 ( m o d p ) ax\equiv1\pmod p ax≡1(modp)那么把这个同余方程中的 x x x 的解叫做 a a a 模 p p p 的乘法逆元,简称逆元 ,记作 a − 1 a^{-1} a−1。
例如 8 x ≡ 1 ( m o d 5 ) 8x \equiv 1 \pmod 5 8x≡1(mod5) 中, x = 2 , 7 , ⋯ x = 2, 7, \cdots x=2,7,⋯ 。那么解出来的这些 x x x 就是 8 8 8 模 5 5 5 的乘法逆元。
2. 逆元存在的条件
- a a a 在模 p p p 下存在乘法逆元的充要条件是 a a a 和 p p p 互质
要想说明 a x ≡ 1 ( m o d p ) ax\equiv1\pmod p ax≡1(modp) 存在这么一个 x x x ,可以进行一个简单的变形。因为是对 a x ax ax 取模,相当于是把 a x ax ax 减掉了 k k k 个 p p p 最终剩下了 1 1 1,相当于可以写成 a x − k p = 1 ax-kp=1 ax−kp=1, k k k 是一个整数,等价于 a x + p y = 1 ax+py=1 ax+py=1。而根据裴蜀定理,不定方程方程 a x + p y = 1 ax+py=1 ax+py=1 有整数解的充要条件是 gcd ( a , p ) = 1 \gcd(a,p)=1 gcd(a,p)=1。
3. 逆元的应用
-
一般我们在求解 a / b ( m o d p ) a/b\pmod p a/b(modp) 这种带除法的模运算时,我们需要先求出除数 b b b 的逆元 b − 1 b^{-1} b−1,转化为求解 a × b − 1 ( m o d p ) a\times b^{-1}\pmod p a×b−1(modp),达到一个把除法转化为乘法的目的。
-
逆元还可以用在其他算法或领域中,比如中国剩余定理、RSA算法等。
二、求逆元的方法
1. 费马小定理 + 快速幂
- 问题背景:求 a a a 在模 p p p 意义下的逆元;
- 前提条件: p p p 为质数,且 a , p a, p a,p 互质;
- 时间复杂度: O ( log p ) O(\log p) O(logp)。
a a a 存在乘法逆元的充要条件是 a a a 与 p p p 互质,而**当模数 p p p 是质数时,**满足费马小定理的条件,由费马小定理:
a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv1\pmod p ap−1≡1(modp)
提出一个 a a a 出来,可以得到
a ⋅ a p − 2 ≡ 1 ( m o d p ) a\cdot a^{p-2}\equiv1\pmod p a⋅ap−2≡1(modp)
而这个式子就恰好满足了我们希望的形式,因此可以看出, a a a 的逆元就是 a p − 2 a^{p-2} ap−2,而 a p − 2 a^{p - 2} ap−2 则可用快速幂进行求解。
当 p p p 不是质数的时候,需要使用其他方法进行求解,例如扩展欧几里得算法。
cpp
#include <iostream>
using namespace std;
typedef long long LL;
// 必须要保证 a, p 互质,且 p 为质数
LL qpow(LL a, LL b, LL p)
{
LL ret = 1;
while(b)
{
if(b & 1) ret = ret * a % p;
b >>= 1;
a = a * a % p;
}
return ret;
}
int main()
{
LL x, p; cin >> n >> p;
cout << qpow(x, p - 2, p) << endl; // 打印 x 在模 p 意义下的乘法逆元
return 0;
}2. 扩展欧几里得算法(exgcd)
- 问题背景:求 a a a 在模 p p p 意义下的逆元;
- 前提条件: a , p a, p a,p 互质;
- 时间复杂度: O ( log p ) O(\log p) O(logp)。
上面说到 a x ≡ 1 ( m o d p ) ax\equiv 1\pmod p ax≡1(modp) 可以转换为求解 a x + p y = 1 ax + py = 1 ax+py=1 这个不定方程,而扩展欧几里得算法正是求解这样一个不定方程的算法。
它的计算过程如下:
注:下面推导中得分式除法表示整除。
- 当 b = 0 b = 0 b=0 时,
a x + b y = a x ax + by = ax ax+by=ax,因此有一组解为 x = 1 , y = 0 x = 1, y = 0 x=1,y=0;
- 当 b ≠ 0 b \ne 0 b=0 时,
由欧几里得算法得: gcd ( a , b ) = gcd ( b , a m o d b ) \gcd(a, b) = \gcd(b, a \bmod b) gcd(a,b)=gcd(b,amodb),则
gcd ( a , b ) = a x + b y ⇓ gcd ( b , a m o d b ) = b x 1 + ( a m o d b ) y 1 = b x 1 + ( a − a b × b ) y 1 = a y 1 + b ( x 1 − a b y 1 ) \gcd(a,b) = ax+by \\ \Downarrow \\ \begin{aligned} \gcd(b, a \bmod b) &= bx_1 + (a \bmod b)y_1 \\ &=bx_1 + (a - \frac{a}{b}\times b)y_1 \\ &= ay_1 + b(x_1 - \frac{a}{b}y_1) \end{aligned} gcd(a,b)=ax+by⇓gcd(b,amodb)=bx1+(amodb)y1=bx1+(a−ba×b)y1=ay1+b(x1−bay1)等式左右应该相等,因此
x = y 1 , y = x 1 − a b y 1 x = y1, y = x1 - \frac{a}{b}y_1 x=y1,y=x1−bay1于是我们可以利用递归,先求出下一层得 x 1 , y 1 x_1, y_1 x1,y1,再求出当前的 x , y x, y x,y。
上述递归过程,可以求出一组特解: x 0 , y 0 x_0, y_0 x0,y0,之后我们可以构造出通解,通解为
{ x = x 0 + b gcd ( a , b ) × k y = y 0 − a gcd ( a , b ) × k \begin{cases} x = x_0 + \frac{b}{\gcd(a, b)}\times k \\ y = y_0 - \frac{a}{\gcd(a, b)}\times k \end{cases} {x=x0+gcd(a,b)b×ky=y0−gcd(a,b)a×k其中 k ∈ N + k\in N^+ k∈N+。
代码实现:
cpp
typedef long long LL;
// exgcd(扩展欧几里得算法) 的返回值和 gcd(欧几里得算法) 一样,都是返回 gcd(a, b)
// 不同的是 exgcd 还可以求出不定方程 ax + by = gcd(a, b) 的一组特解 x, y, 这里由于 a, b 互质,就是求解 ax + by = 1
// 由于 C++ 只能有一个返回值,所以我们要求的 x, y 需要传引用
LL exgcd(LL a, LL b, LL& x, LL& y)
{
if(b == 0)
{
x = 1, y = 0;
return a;
}
// b 不为 0
LL x1, y1, d;
// 递归求出 x1, y1
d = exgcd(b, a % b, x1, y1);
// 利用公式求出当前层的 x, y
x = y1;
y = x1 - a / b * y1;
return d;
}3. 递推法
- 问题背景:求 [ 1 , n ] [1, n] [1,n] 中所有数在模 p p p 意义下的逆元;
- 前提条件: [ 1 , n ] [1, n] [1,n] 中所有数都与 p p p 互质;
- 时间复杂度: O ( n ) O(n) O(n)。
方法:
用 i n v [ ] inv[] inv[] 数组存储逆元, i n v [ i ] inv[i] inv[i] 表示 i i i 在模 p p p 意义下的逆元。
- 当 i = 1 i = 1 i=1 时, i n v [ 1 ] = 1 inv[1] = 1 inv[1]=1;
- 当 i > 1 i > 1 i>1 时, i n v [ i ] = p − ( ⌊ p / i ⌋ ) × i n v [ p m o d i ] m o d p inv[i] = p - (\lfloor p/i\rfloor)\times inv[p\bmod i]\bmod p inv[i]=p−(⌊p/i⌋)×inv[pmodi]modp。
证明:
当 i = 1 i = 1 i=1 时,显然。
当 i > 1 i > 1 i>1 时,设 p ÷ i = k ⋯ r p\div i = k\cdots r p÷i=k⋯r(商 k k k 余 r r r),那么有
p = i × k + r p = i\times k + r p=i×k+r
显然
i × k + r ≡ 0 ( m o d p ) i\times k + r\equiv 0\pmod p i×k+r≡0(modp)
现在两边同时乘以 i − 1 i^{-1} i−1 和 r − 1 r^{-1} r−1,得到
k × r − 1 + i − 1 ≡ 0 ( m o d p ) k\times r^{-1} + i^{-1}\equiv 0\pmod p k×r−1+i−1≡0(modp)
移项得到
i − 1 ≡ − k × r − 1 ( m o d p ) i^{-1}\equiv -k\times r ^{-1}\pmod p i−1≡−k×r−1(modp)
所以现在可以得到 i n v [ i ] = i − 1 = ( − k × r − 1 ) m o d p = p + ( − k × r − 1 ) m o d p inv[i] = i^{-1} = (-k\times r^{-1})\bmod p = p + (-k\times r^{-1})\bmod p inv[i]=i−1=(−k×r−1)modp=p+(−k×r−1)modp,其中 k = ⌊ p / i ⌋ , r − 1 = i n v [ p m o d i ] k = \lfloor p/i\rfloor ,\ r^{-1} = inv[p\bmod i] k=⌊p/i⌋, r−1=inv[pmodi],综上有
i n v [ i ] = p − ( ⌊ p / i ⌋ ) × i n v [ p m o d i ] m o d p inv[i] = p - (\lfloor p/i\rfloor)\times inv[p\bmod i]\bmod p inv[i]=p−(⌊p/i⌋)×inv[pmodi]modp
cpp
typedef long long LL;
LL inv[N];
int main()
{
LL n, p;
scanf("%lld %lld", &n, &p);
inv[1] = 1;
for(int i = 2; i <= n; i++) inv[i] = p - p / i * inv[p % i] % p;
for(int i = 1; i <= n; i++) printf("%lld\n", inv[i]);
return 0;
}三、练习
1. 序列求和 ⭐⭐
【题目链接】
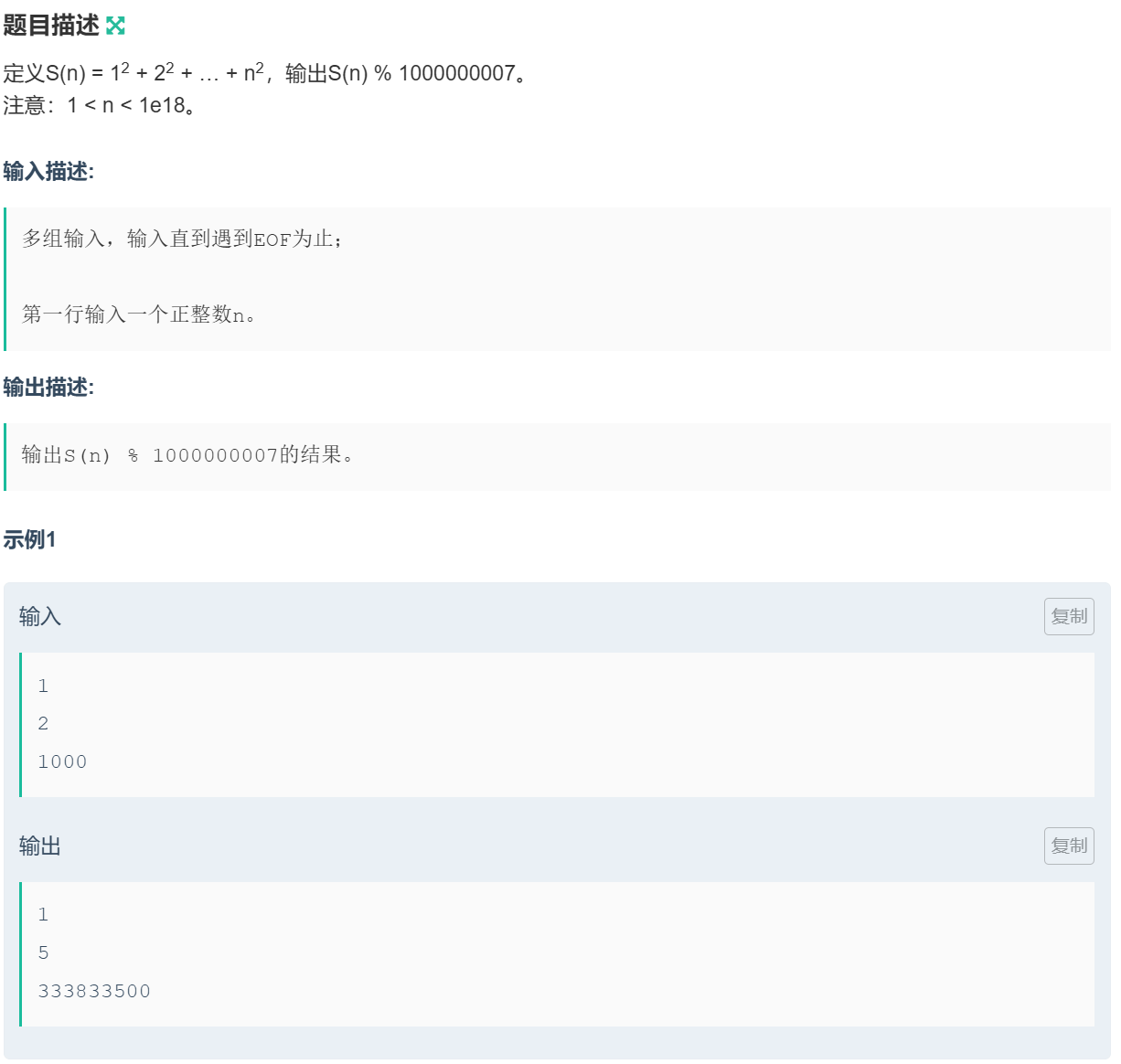
中学时我们学过, 1 2 + 2 2 + ⋯ + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 1^2 + 2^2 + \cdots + n^2 = \frac{n(n + 1)(2n + 1)}{6} 12+22+⋯+n2=6n(n+1)(2n+1),所以这道题本质上是在求右边这个分式的值然后对 ( 1 0 9 + 7 ) (10^9 + 7) (109+7) 取模的结果。如果我们直接求解,那么我们需要计算 n ( n + 1 ) ( 2 n + 1 ) n(n + 1)(2n + 1) n(n+1)(2n+1),由于 n n n 非常大,所以我们要边乘边取模,但是模完之后的数可能不是 6 6 6 的倍数了,因此我们不能用除以 6 6 6 来运算最终结果,所以需要用乘法逆元把除法转换为乘法。原式等价于求解
n ( n + 1 ) ( 2 n + 1 ) × 6 − 1 m o d ( 1 0 9 + 7 ) n(n + 1)(2n + 1) \times 6^{-1} \bmod (10^9 + 7) n(n+1)(2n+1)×6−1mod(109+7)
求解 6 6 6 在模 ( 1 0 9 + 7 ) (10^9 + 7) (109+7) 下的逆元采用费马小定理 + 快速幂即可。
cpp
#include<iostream>
using namespace std;
typedef long long LL;
const int p = 1e9 + 7;
LL n;
// 快速幂
LL qpow(LL a, LL n, LL p)
{
LL ret = 1;
while(n)
{
if(n & 1) ret = ret * a % p;
n >>= 1;
a = a * a % p;
}
return ret;
}
// 费马小定理求解 x 模 p 下的逆元
LL rev(LL x, LL p)
{
return qpow(x, p - 2, p);
}
int main()
{
while(cin >> n)
{
// 由于 n 可能非常大,所以每一步乘法运算后都需要取一次模防止溢出
LL ans = ((((n % p) * ((n + 1) % p) % p) % p) * ((2 * n + 1) %p)) % p * (rev(6, p)) % p;
cout << ans << endl;
}
return 0;
}2.【模板】逆元 ⭐⭐
【题目链接】
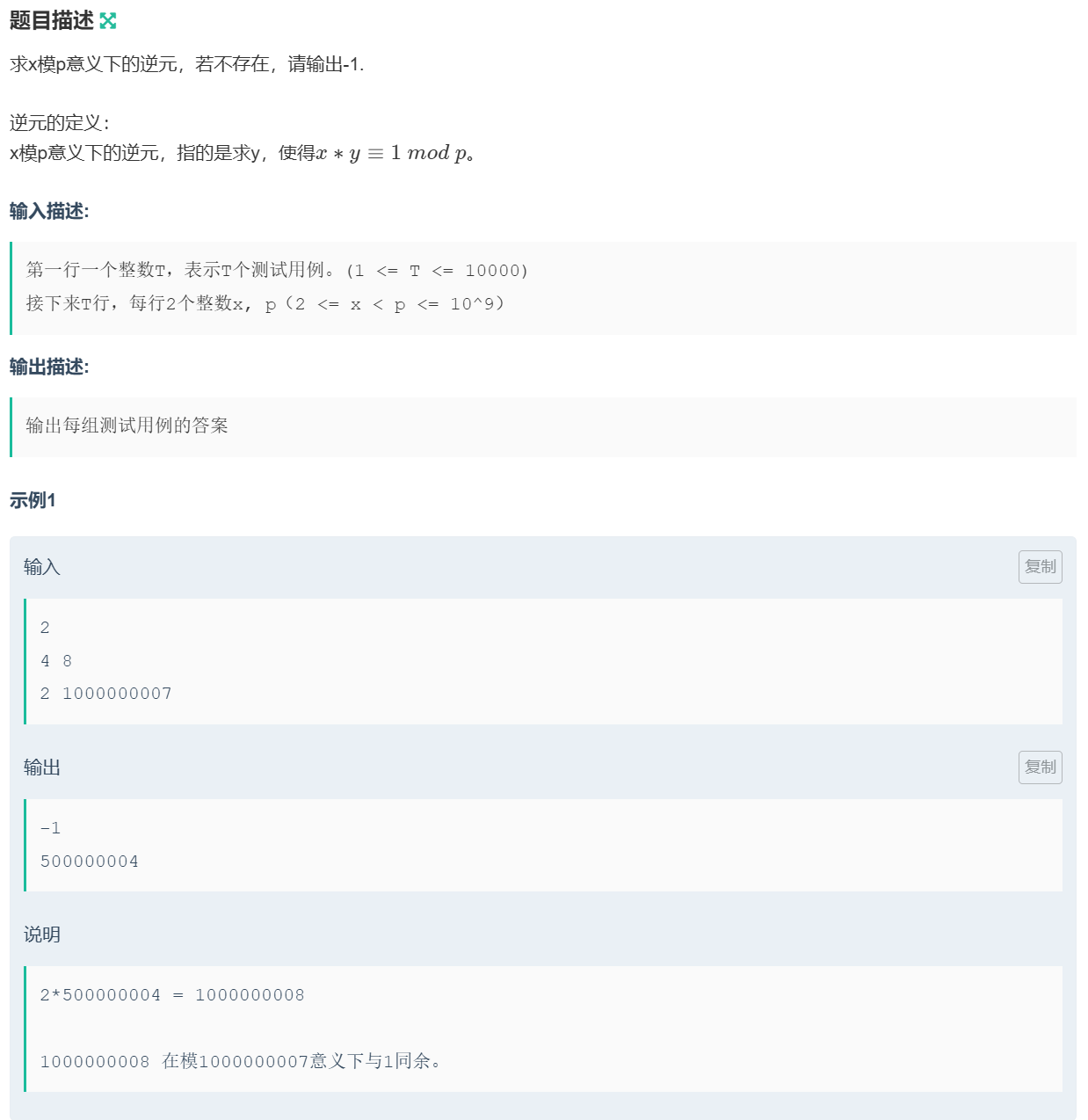
利用扩展欧几里得算法求解逆元即可。
cpp
#include<iostream>
using namespace std;
typedef long long LL;
// 扩展欧几里得算法
LL exgcd(LL a, LL b, LL& x, LL& y)
{
if(b == 0)
{
x = 1, y = 0;
return a;
}
LL x1, y1, d;
d = exgcd(b, a % b, x1, y1);
x = y1;
y = x1 - a / b * y1;
return d;
}
int main()
{
LL t, x, p;
scanf("%lld", &t);
while(t--)
{
scanf("%lld %lld", &x, &p);
// x0 * x + y0 * p = 1
LL x0, y0, d;
d = exgcd(x, p, x0, y0);
if(d != 1) printf("-1\n");
else
{
x0 = (x0 % p + p) % p; // 把 x0 求成最小的正整数解
printf("%lld\n", x0);
}
}
return 0;
}3.【模板】模意义下的乘法逆元 ⭐⭐
【题目链接】
【题目描述】
给定 n , p n,p n,p 求 1 ∼ n 1\sim n 1∼n 中所有整数在模 p p p 意义下的乘法逆元。
这里 a a a 模 p p p 的乘法逆元定义为 a x ≡ 1 ( m o d p ) ax\equiv1\pmod p ax≡1(modp) 的解。
【输入格式】
一行两个正整数 n , p n,p n,p。
【输出格式】
输出 n n n 行,第 i i i 行表示 i i i 在模 p p p 下的乘法逆元。
【示例一】
输入
10 13输出
1 7 9 10 8 11 2 5 3 4
【说明/提示】
1 \\leq n \\leq 3 \\times 10 \^ 6 , , ,n \< p \< 20000528 。
输入保证 p 为质数。
由于 p p p 是质数并且 n < p n < p n<p,所以 [ 1 , n ] [1, n] [1,n] 中所有数都是与 p p p 互质的,因此直接用递推法求解逆元即可。
cpp
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 3e6 + 10;
LL inv[N];
int main()
{
LL n, p;
scanf("%lld %lld", &n, &p);
inv[1] = 1;
for(int i = 2; i <= n; i++) inv[i] = p - p / i * inv[p % i] % p;
for(int i = 1; i <= n; i++) printf("%lld\n", inv[i]);
return 0;
}