问题:一个商人要去全国31个省会城市,每个城市只能去一次,而且最后要回到最初出发的城市,需要进行路径选择:要求所选路径的路程是所有路径之中最短的。
全国31个省会城市坐标为:
1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;... 3238 1229;4196 1044;4312 790;4386 570;3007 1970;2562 1756;... 2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;... 3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;... 3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;... 2370 2975
1. 遗传算法求解过程:
1.初始化种群:
NP=300,染色体长度为31,最大进化代数G=5000。
2.产生初始种群:
计算个体适应度,采用基于概率的方法进行个体选择,对选中的成对个体随机交叉所选中的成对城市坐标,以保证交叉后每个城市只去一次,对选中单个个体,随机交换一对城市坐标作为变异操作,产生新种群。
3.判断是否满足终止条件:
达到最大迭代次数则停止。
2. 具体实现代码:
%%%%%%%%%%%%%%%%%%%%%%%%%遗传算法解决TSP问题%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
clc; %清屏
C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
3238 1229;4196 1044;4312 790;4386 570;3007 1970;2562 1756;...
2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;...
3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
2370 2975]; %31个省会城市坐标31*2
N=size(C,1); %TSP问题的规模,即城市数目
D=zeros(N); %任意两个城市距离间隔矩阵
%%%%%%%%%%%%%%%%%%%%%求任意两个城市距离间隔矩阵%%%%%%%%%%%%%%%%%%%%%
for i=1:N
for j=1:N
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
end
end
NP=300; %种群规模
G=5000; %最大遗传代数
f=zeros(NP,N); %用于存储种群
for i=1:NP
f(i,:)=randperm(N);
%随机生成初始种群 randperm(n)返回行向量,其中包含从 1 到 n 没有重复元素的整数随机排列。
end
R=f(1,:); %存储最优种群
len=zeros(1,NP); %存储路径长度,每一个种群个体构成路径的长度
fitness=zeros(NP,1); %存储归一化适应值
gen=0;
%%%%%%%%%%%%%%%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
while gen<G
%%%%%%%%%%%%%%%%%%%%%计算路径长度%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NP %每个个体中城市顺序构成的路径长度和
len(i)=D(f(i,N),f(i,1));
for j=1:(N-1)
len(i)=len(i)+D(f(i,j),f(i,j+1));
end
end
maxlen=max(len); %本次循环最长路径
minlen=min(len); %本次循环最短路径
%%%%%%%%%%%%%%%%%%%%%%%%%更新最短路径%%%%%%%%%%%%%%%%%%%%%%%%%%
rr=find(len==minlen);
R=f(rr(1,1),:); %最优的个体(最优城市排列顺序,最短路径)
%%%%%%%%%%%%%%%%%%%%%计算归一化适应值%%%%%%%%%%%%%%%%%%%%%%%%%%
fitness=zeros(1,NP);
for i=1:NP
fitness(i)=(len(i)-minlen)/(maxlen-minlen+0.001);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
nn=0;
for i=1:NP
if fitness(i)<=rand %以随机概率选择种群中的个体
nn=nn+1;
F(nn,:)=f(i,:);
end
end
[aa,bb]=size(F);
k=0;
while aa<=NP
nnper=randperm(aa);
A=F(nnper(1),:);
B=F(nnper(2),:);
%%%%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%%%%%%%%
W=ceil(bb/10); %交叉点个数
p=unidrnd(bb-W+1); %随机选择交叉范围,从p到p+W
%unidrnd(N):生成一个范围为1到N的随机整数。
%unidrnd(N, m, n)或 unidrnd(N, [m, n]):生成大小为`m×n`的矩阵,每个元素均为1到N之间的
随机整数。
for i=1:W %交换A(p+i-1)和B(p+i-1)位置的城市,同样交换A(x)与B(y)位置的城市
x=find(A==B(p+i-1));
y=find(B==A(p+i-1));
temp=A(p+i-1);
A(p+i-1)=B(p+i-1);
B(p+i-1)=temp;
temp=A(x);
A(x)=B(y);
B(y)=temp;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%%%%%
p1=floor(1+N*rand());
p2=floor(1+N*rand());
%floor 将 X 的每个元素四舍五入到小于或等于该元素的最接近整数。
while p1==p2
p1=floor(1+N*rand());
p2=floor(1+N*rand());
end
%随机选择两个城市进行对个体A、B中这两个城市位置进行对调
tmp=A(p1);
A(p1)=A(p2);
A(p2)=tmp;
tmp=B(p1);
B(p1)=B(p2);
B(p2)=tmp;
F=[F;A;B];
[aa,bb]=size(F);
end
if aa>NP
F=F(1:NP,:); %保持种群规模为n
end
f=F; %更新种群
f(1,:)=R; %保留每代最优个体
clear F;
gen=gen+1;
Rlength(gen)=minlen;
end
figure
for i=1:N-1
plot([C(R(i),1),C(R(i+1),1)],[C(R(i),2),C(R(i+1),2)],'bo-');
hold on;
end
plot([C(R(N),1),C(R(1),1)],[C(R(N),2),C(R(1),2)],'ro-');
title(['优化最短距离:',num2str(minlen)]);
figure
plot(Rlength)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')3. 结果及拓展
结果1:
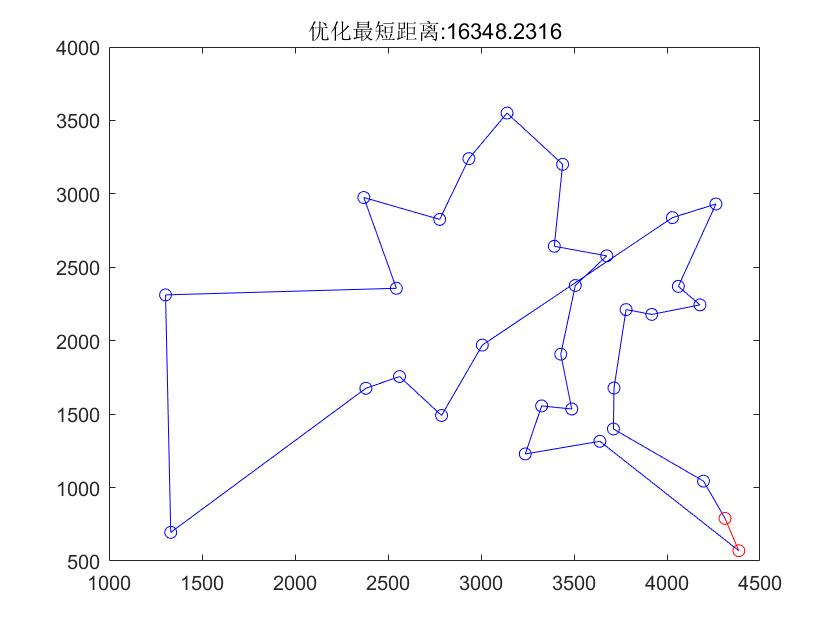
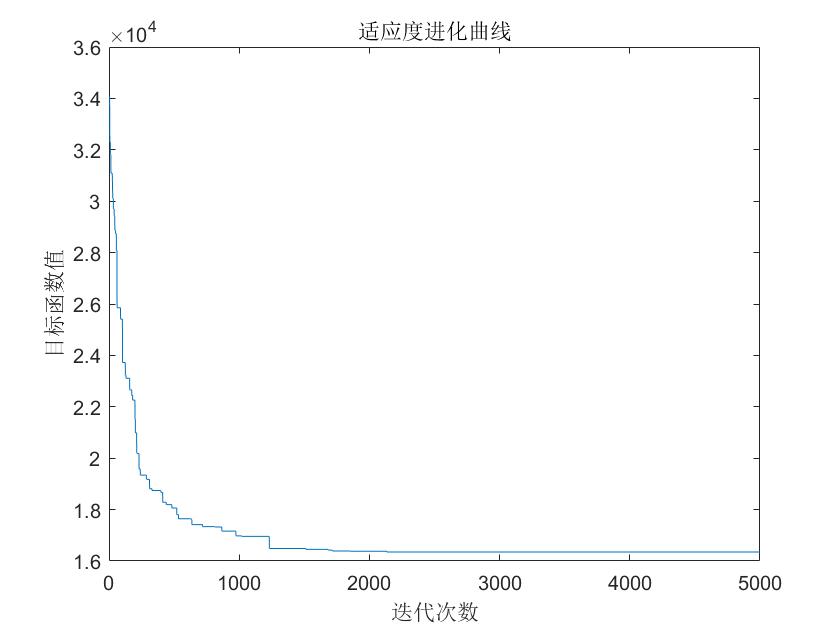
结果2:
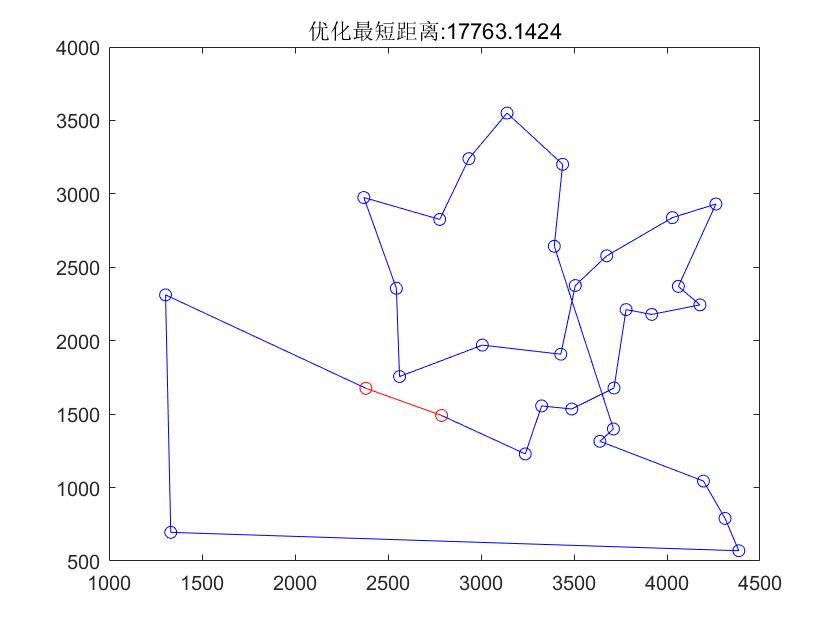
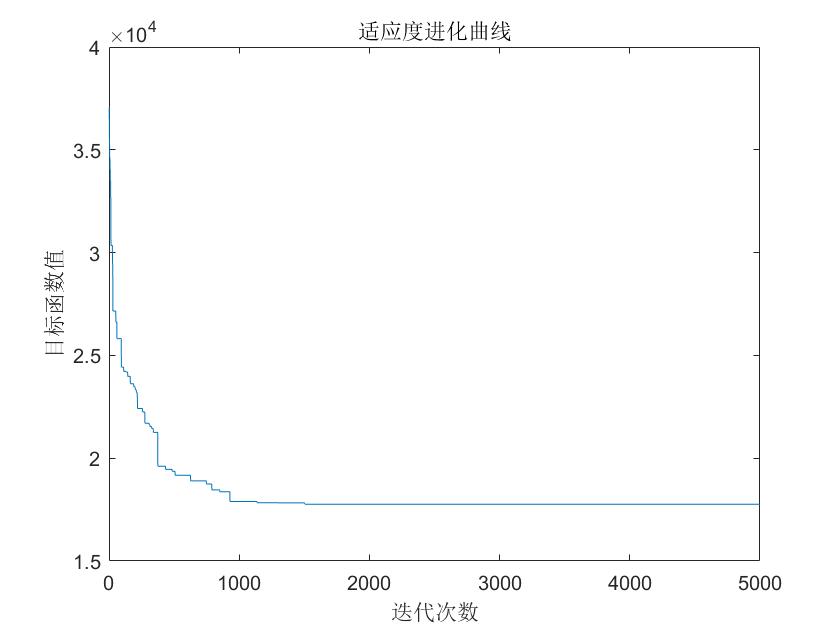
虽然可以实现求解,但每次运行代码后结果会有偏差(可能和代码中使用随机概率选择有关),需要进一步改进。欢迎各位佬批评指正!!!