SVM案例分析

文章目录

[SVM 简介](#SVM 简介)
- - 一、基本原理
  - [二、SVM 的主要特点](#二、SVM 的主要特点)
  - 三、应用场景
  - 四、简单例子（Python）
SVM参数
- [一、SVM 的核心参数（`SVC()` ）](#一、SVM 的核心参数（SVC() ）)
- 二、参数详解
- 三、常见核函数比较
- 四、常见调参策略
- 五、调参经验总结
网格搜索
- 一、核心调参逻辑
- 二、网格搜索（GridSearchCV）
- - [1. 基本思想](#1. 基本思想)
  - [📜 2. 代码示例](#📜 2. 代码示例)
- 三、调参结果可视化
- 四、经验法则（实战调参技巧）
- 五、实战建议
理解
- 一、可视化目标
- [二、完整 Python 示例代码](#二、完整 Python 示例代码)
- 三、结果解读
- 四、经验总结
- 五、可视化结论
另一个数据
- 一、示例目标
- 二、完整可运行代码示例
- 三、运行效果说明
- 四、核心观察结论
- 五、进一步实验建议
- [{'C': 1, 'gamma': 0.1}](#{'C': 1, 'gamma': 0.1})
练习题
- 一、数据简介
- [二、Python 实例代码（含参数调优 + 可视化）](#二、Python 实例代码（含参数调优 + 可视化）)
- 三、结果说明
- 四、分析要点
- 练习题

SVM 简介

SVM（Support Vector Machine，支持向量机）是一种常见的监督学习算法 ，主要用于分类和回归分析。它的核心思想是：

一、基本原理

线性可分情况

当数据可以用一条直线（二维）或一个超平面（高维）完美分开时，SVM寻找能使两类样本之间的间隔最大的那条分割线。
- 超平面的方程为：
  
  w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0
- 最大化间隔等价于最小化 ∥ w ∥ 2 \|w\|^2 ∥w∥2，同时保证所有样本被正确分类。
线性不可分情况

对于复杂数据，SVM会使用**核函数（Kernel Function）**将原始数据映射到高维空间，使其在高维空间中线性可分。

常见核函数包括：
- 线性核（Linear Kernel）
- 多项式核（Polynomial Kernel）
- 高斯核 / RBF 核（Radial Basis Function）
- Sigmoid 核
支持向量（Support Vectors）

离分割超平面最近的样本点，被称为支持向量。它们决定了最终分类边界的位置和方向。

二、SVM 的主要特点

特点	说明
泛化能力强	通过最大间隔原则，减少过拟合风险
对高维数据有效	在特征数远大于样本数时表现良好
可用核函数处理非线性问题	适应性强
计算复杂度较高	特别是在大数据集上训练时
结果可解释性一般	相比决策树或逻辑回归略差

三、应用场景

文本分类（垃圾邮件检测、情感分析）
图像识别（人脸识别、目标检测）
医学诊断（疾病分类）
信用评分与欺诈检测

四、简单例子（Python）

python 复制代码

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
iris = datasets.load_iris()
X, y = iris.data, iris.target

# 拆分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 建立 SVM 模型（使用RBF核）
model = SVC(kernel='rbf', C=1.0)
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)
print("准确率：", accuracy_score(y_test, y_pred))

SVM参数

SVM 的主要参数 （以 scikit-learn 的 SVC 为例）

一、SVM 的核心参数（`SVC()` ）

python 复制代码

from sklearn.svm import SVC

model = SVC(
    C=1.0,
    kernel='rbf',
    degree=3,
    gamma='scale',
    coef0=0.0,
    shrinking=True,
    probability=False,
    tol=1e-3,
    cache_size=200,
    class_weight=None,
    verbose=False,
    max_iter=-1,
    decision_function_shape='ovr',
    break_ties=False,
    random_state=None
)

二、参数详解

参数	类型 / 默认值	含义与作用	调参建议
C	`float`, 默认 `1.0`	惩罚系数（正则化参数），控制"分类错误"与"间隔大小"的权衡。 • C 较大 → 更关注分类正确率，间隔更小，容易过拟合。 • C 较小 → 允许更多错误样本，间隔更大，泛化能力更强。	建议调参范围：`[0.01, 0.1, 1, 10, 100]`
kernel	`str`, 默认 `'rbf'`	核函数类型，用于将数据映射到高维空间。 • `'linear'`：线性核（适用于线性可分数据） • `'poly'`：多项式核 • `'rbf'`：高斯径向基核（最常用） • `'sigmoid'`：类神经网络核	通常从 `'rbf'` 和 `'linear'` 开始；高维稀疏数据推荐 `'linear'`
degree	`int`, 默认 `3`	多项式核函数中的多项式阶数（仅对 `kernel='poly'` 有效）	仅在使用 `'poly'` 时调整，如 `2~5` 之间
gamma	`'scale'` / `'auto'` / `float`	RBF、多项式、sigmoid 核函数的参数。控制单个样本的"影响范围"。 • gamma 大 → 决策边界复杂，过拟合风险高。 • gamma 小 → 边界平滑，可能欠拟合。	常用范围：`[1e-3, 1e-2, 1e-1, 1, 10]`。默认 `'scale'` 表示 `1 / (n_features * X.var())`，一般表现较好。
coef0	`float`, 默认 `0.0`	在 `'poly'` 与 `'sigmoid'` 核中使用，控制多项式的常数项影响	通常只在这两种核下调参，如 `0~1`
shrinking	`bool`, 默认 `True`	是否启用收缩启发式算法来加快优化速度（通常保持默认）	一般不用改
probability	`bool`, 默认 `False`	是否启用概率估计（`predict_proba` 可用），但训练会更慢	如果需要输出概率值则设为 `True`
tol	`float`, 默认 `1e-3`	停止迭代的容差（越小越精确但越慢）	调整计算精度需求
cache_size	`float`, 默认 `200`	缓存大小（单位 MB），提高大数据训练速度	内存足够时可设为更大
class_weight	`'balanced'` 或 `dict`	设置不同类别的权重，适用于类别不平衡数据。 • `'balanced'` 自动按样本数量反比赋权。	推荐在类别不平衡时使用 `'balanced'`
verbose	`bool`, 默认 `False`	是否打印训练过程中的详细信息	调试时可设为 `True`
max_iter	`int`, 默认 `-1`	最大迭代次数，`-1` 表示不限制	可用于限制训练时间
decision_function_shape	`'ovr'` 或 `'ovo'`	多分类策略： • `'ovr'`（一对多）→ 默认且更快 • `'ovo'`（一对一）→ 更精确但更慢	一般保持默认 `'ovr'`
break_ties	`bool`, 默认 `False`	当 `decision_function_shape='ovr'` 且分数相同时，是否根据距离打破平局	用于多分类时更精确的结果
random_state	`int` 或 `None`	随机种子，用于可重复性	可固定随机性以复现实验

三、常见核函数比较

核函数	表达式	优点	缺点
linear	K ( x i , x j ) = x i ⋅ x j K(x_i, x_j) = x_i \cdot x_j K(xi,xj)=xi⋅xj	训练快，结果可解释性强	对非线性数据效果差
poly	( γ x i ⋅ x j + r ) d (γx_i \cdot x_j + r)^d (γxi⋅xj+r)d	能拟合多项式关系	参数较多、计算慢
rbf	( e^{-γ		x_i - x_j	^2} )	适应性强、效果好	需调参（γ）
sigmoid	tanh ⁡ ( γ x i ⋅ x j + r ) \tanh(γx_i \cdot x_j + r) tanh(γxi⋅xj+r)	类似神经网络效果	不稳定，使用较少

四、常见调参策略

网格搜索（GridSearchCV）

python 复制代码

from sklearn.model_selection import GridSearchCV
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [1, 0.1, 0.01, 0.001],
    'kernel': ['rbf', 'linear']
}
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=1)
grid.fit(X_train, y_train)
print(grid.best_params_)

随机搜索（RandomizedSearchCV）

当参数空间很大时更高效。
标准化输入特征 （非常重要）

在使用 RBF、多项式或 sigmoid 核时必须进行标准化（如 StandardScaler），否则 γ、C 的效果会被特征尺度扭曲。

五、调参经验总结

一般从 RBF 核开始；
先固定 γ，调整 C；
若欠拟合 → 提高 C 或 γ；
若过拟合 → 降低 C 或 γ；
类别不平衡 → 用 class_weight='balanced'；
数据量大时可考虑 LinearSVC（线性核的高效实现）。

网格搜索

✅ 参数调优逻辑思路

✅ 网格搜索（Grid Search）

✅ 可视化调参结果

✅ 常见经验法则与实战技巧

一、核心调参逻辑

SVM 主要有两个关键参数决定性能：

参数	含义	控制作用
C	惩罚系数	控制分类错误的容忍度（正则化强度）
γ (gamma)	核函数参数	控制单个样本的"影响范围"（RBF核常用）

二者之间存在耦合关系：

γ 决定了模型的复杂度（边界弯曲程度），

C 决定了模型的容错率。

调参目标：在二者之间找到欠拟合 ↔ 过拟合的平衡点。

二、网格搜索（GridSearchCV）

1. 基本思想

通过遍历指定的参数组合，利用交叉验证（Cross Validation）选出最优的超参数。

📜 2. 代码示例

python 复制代码

from sklearn import datasets
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
import numpy as np

# 1️⃣ 加载数据
iris = datasets.load_iris()
X, y = iris.data, iris.target

# 2️⃣ 数据标准化
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 3️⃣ 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 4️⃣ 定义参数网格
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [1, 0.1, 0.01, 0.001],
    'kernel': ['rbf']
}

# 5️⃣ 网格搜索 + 交叉验证
grid = GridSearchCV(
    SVC(),
    param_grid,
    refit=True,
    cv=5,             # 5折交叉验证
    verbose=1,
    n_jobs=-1
)

grid.fit(X_train, y_train)

# 6️⃣ 输出最优参数与准确率
print("最佳参数：", grid.best_params_)
print("最佳交叉验证准确率：", grid.best_score_)
print("测试集准确率：", grid.best_estimator_.score(X_test, y_test))

三、调参结果可视化

通过热力图（Heatmap）可直观观察不同 C 和 γ 的组合对准确率的影响：

python 复制代码

import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

# 提取结果
results = pd.DataFrame(grid.cv_results_)

# 生成透视表（pivot table）
pivot = results.pivot_table(values='mean_test_score',
                            index='param_gamma',
                            columns='param_C')

# 可视化
plt.figure(figsize=(8, 6))
sns.heatmap(pivot, annot=True, fmt=".3f", cmap="YlGnBu")
plt.title("SVM 参数调优 (C vs gamma)")
plt.xlabel("C 值")
plt.ylabel("Gamma 值")
plt.show()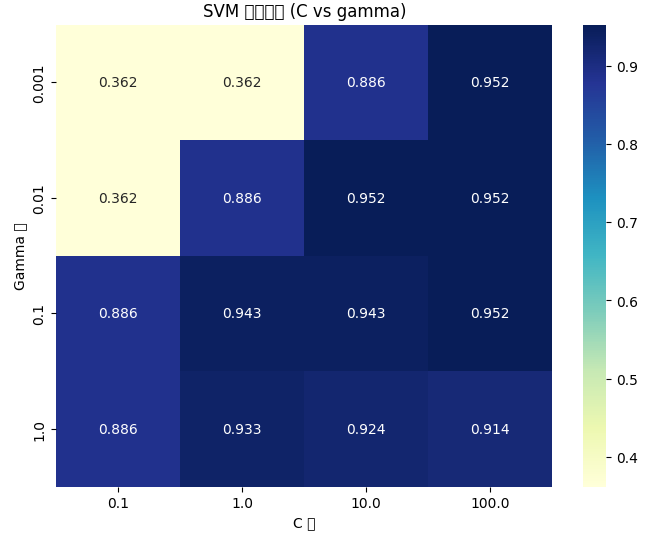

热力图说明：

较深的颜色（高分）代表参数组合效果更好；
观察高分区域的分布趋势，可以推断调整方向；
通常 γ 较小 + C 适中能获得平滑、稳定的决策边界。

四、经验法则（实战调参技巧）

问题情形	调整建议	原因解释
模型欠拟合（准确率低）	↑C 或 ↑γ	提高模型复杂度，让边界更贴近数据
模型过拟合（训练高，测试低）	↓C 或 ↓γ	降低复杂度，边界更平滑
特征尺度差异大	标准化/归一化	防止某个特征主导距离计算
类别不平衡	`class_weight='balanced'`	自动调整类别权重
样本量很大	尝试 `LinearSVC`	减少计算开销（线性核版本）
调参太慢	用 `RandomizedSearchCV`	随机搜索更高效
想获取概率输出	`probability=True`	启用概率估计（但训练更慢）

五、实战建议

步骤化调参流程：
- ① 先固定核函数（建议从 'rbf' 开始）；
- ② 粗调 C（如 [0.01, 0.1, 1, 10, 100]）；
- ③ 再调 γ（如 [1, 0.1, 0.01, 0.001]）；
- ④ 观察结果热力图，确定高分区域；
- ⑤ 在高分区域细调（如 C = 2～5，γ = 0.05～0.2）；
- ⑥ 最后用交叉验证确认稳定性。
RBF核的典型经验起点：
- C ≈ 1
- γ ≈ 1 / 特征维度
调参代价 vs 效果：
- 小数据集可全网格搜索；
- 大数据集建议用 分层随机搜索 + 交叉验证。

理解

一、可视化目标

我们将使用一个二维的示例数据集（例如两个类别的点），通过改变：

C（惩罚系数）
γ（RBF 核宽度参数）

观察它们如何影响：

决策边界的形状（复杂 or 平滑）；
过拟合与欠拟合现象。

二、完整 Python 示例代码

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler

# 1️⃣ 生成示例数据
X, y = datasets.make_moons(n_samples=200, noise=0.2, random_state=42)

# 2️⃣ 标准化数据
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 3️⃣ 定义绘制函数
def plot_svm_decision_boundary(C, gamma, ax):
    model = SVC(kernel='rbf', C=C, gamma=gamma)
    model.fit(X, y)
    
    # 绘制决策区域
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),
                         np.linspace(y_min, y_max, 300))
    Z = model.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    ax.contourf(xx, yy, Z > 0, alpha=0.2, cmap=plt.cm.coolwarm)
    ax.contour(xx, yy, Z, colors=['k', 'k', 'k'],
               linestyles=['--', '-', '--'], levels=[-1, 0, 1])
    ax.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=25, edgecolors='k')
    ax.set_title(f"C={C}, gamma={gamma}")
    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())

# 4️⃣ 创建子图，组合对比不同参数
fig, axes = plt.subplots(3, 3, figsize=(12, 12))
plt.suptitle("RBF核 SVM 参数 (C, γ) 对决策边界的影响", fontsize=16)

C_values = [0.1, 1, 10]
gamma_values = [0.1, 1, 10]

for i, C in enumerate(C_values):
    for j, gamma in enumerate(gamma_values):
        plot_svm_decision_boundary(C, gamma, axes[i, j])

plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()

三、结果解读

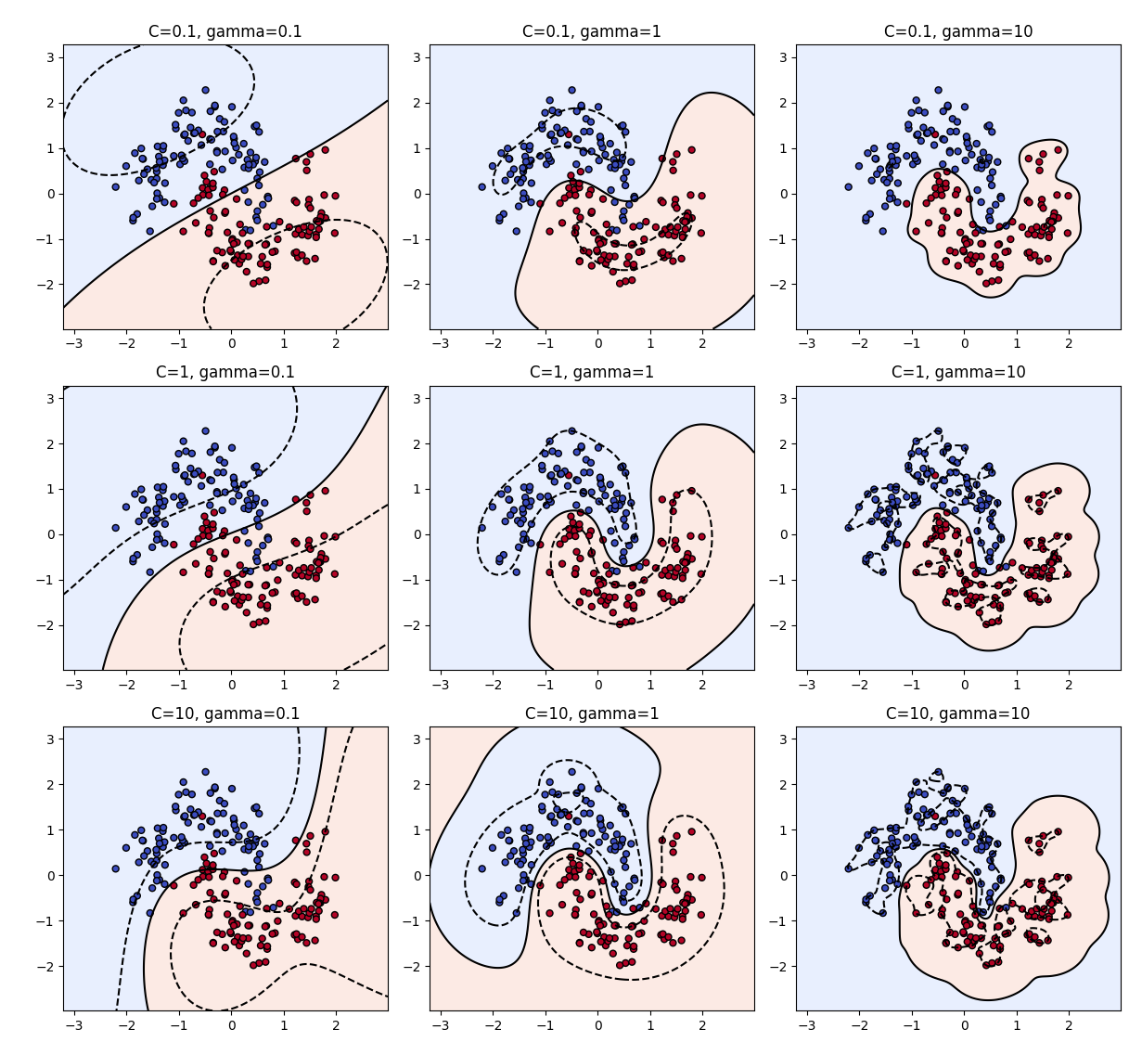
C	γ	决策边界表现
小 C + 小 γ	非常平滑（欠拟合）	模型过于简单，不够灵活
大 C + 小 γ	边界平滑但更贴近数据	合理分类效果
小 C + 大 γ	局部振荡，部分欠拟合	过度惩罚平滑度
大 C + 大 γ	极度弯曲（过拟合）	模型过度贴合训练样本

直观理解：

γ 控制"弯曲程度"：越大 → 模型对每个点更敏感 → 边界更复杂。
C 控制"容忍度"：越大 → 更不允许分类错误 → 边界贴近样本。

四、经验总结

调参目标	调整策略
欠拟合 → 模型太简单	增大 γ 或 C
过拟合 → 模型太复杂	减小 γ 或 C
训练慢	优先减小 C 或 γ（边界更简单）
类别重叠明显	降低 γ，允许更宽间隔

五、可视化结论

小 C / 小 γ： 线性近似，间隔宽大（"欠拟合"）。
中等 C / γ： 平滑、稳健，通常最优。
大 C / 大 γ： 决策边界蜿蜒曲折（"过拟合"）。

另一个数据

一、示例目标

我们要演示：

不同的 C（惩罚系数）
不同的 γ（核宽度参数）

对 RBF 核 SVM 决策边界形状 的影响。

二、完整可运行代码示例

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler

# 1️⃣ 生成"同心圆"数据集
X, y = make_circles(n_samples=300, factor=0.5, noise=0.08, random_state=42)

# 2️⃣ 标准化数据
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 3️⃣ 定义绘制函数
def plot_svm_decision_boundary(C, gamma, ax):
    model = SVC(kernel='rbf', C=C, gamma=gamma)
    model.fit(X, y)
    
    # 绘制决策边界
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),
                         np.linspace(y_min, y_max, 300))
    Z = model.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # 绘图
    ax.contourf(xx, yy, Z > 0, alpha=0.2, cmap=plt.cm.coolwarm)
    ax.contour(xx, yy, Z, colors=['k', 'k', 'k'],
               linestyles=['--', '-', '--'], levels=[-1, 0, 1])
    ax.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=25, edgecolors='k')
    ax.set_title(f"C={C}, γ={gamma}")
    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())

# 4️⃣ 对比不同参数组合
fig, axes = plt.subplots(3, 3, figsize=(12, 12))
plt.suptitle("RBF核 SVM 参数对同心圆数据决策边界的影响", fontsize=16)

C_values = [0.1, 1, 10]
gamma_values = [0.1, 1, 10]

for i, C in enumerate(C_values):
    for j, gamma in enumerate(gamma_values):
        plot_svm_decision_boundary(C, gamma, axes[i, j])

plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()

三、运行效果说明

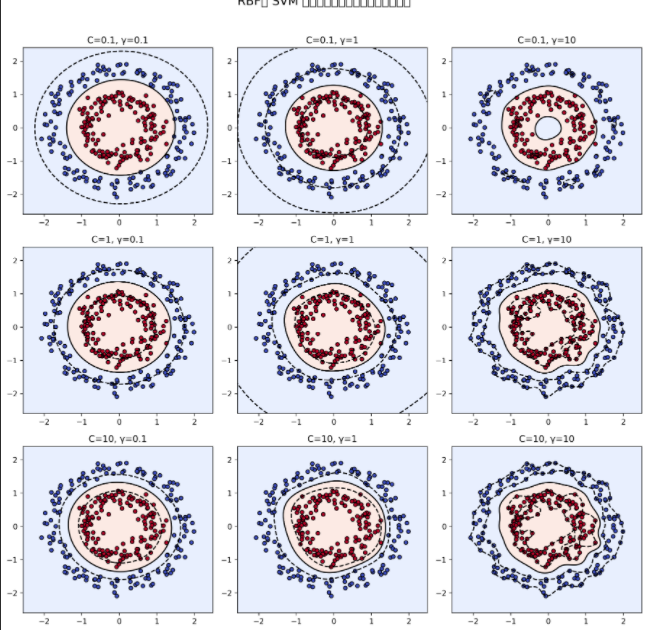
行（C）	列（γ）	边界特征
小 C + 小 γ	决策边界几乎是圆滑的大圆，很多点被错分（欠拟合）
大 C + 小 γ	仍然平滑，但更贴近真实边界
小 C + 大 γ	决策边界变得波动、不稳定
大 C + 大 γ	极度弯曲的复杂边界（过拟合）

四、核心观察结论

γ 控制"每个点的影响半径"
- 小 γ → 边界平滑
- 大 γ → 边界过度弯曲
C 控制"容忍错误的程度"
- 小 C → 允许分类错误，间隔更宽
- 大 C → 更严格拟合训练样本
当 C 和 γ 都过大时，模型能完美分类训练集，但对新样本泛化能力差（过拟合）。

五、进一步实验建议

可以尝试：

python 复制代码

# 调参实验
C_values = [0.01, 0.1, 1, 10, 100]
gamma_values = [0.01, 0.1, 1, 10]

或使用 网格搜索 + 热力图 查看最优组合：

python 复制代码

from sklearn.model_selection import GridSearchCV

param_grid = {'C': [0.1, 1, 10], 'gamma': [0.1, 1, 10]}
grid = GridSearchCV(SVC(kernel='rbf'), param_grid, cv=5)
grid.fit(X, y)
print(grid.best_params_)

{'C': 1, 'gamma': 0.1}

练习题

一、数据简介

红酒数据集来自意大利，包含 178 个样本，每个样本有 13 个化学成分特征，对应 3 种葡萄酒类别。

特征如：酒精含量、苹果酸、灰分、颜色强度、OD280/OD315等。

二、Python 实例代码（含参数调优 + 可视化）

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.decomposition import PCA
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 1️⃣ 加载红酒数据集
wine = datasets.load_wine()
X, y = wine.data, wine.target

# 2️⃣ 数据标准化（非常重要）
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 3️⃣ 拆分训练集 / 测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)

# 4️⃣ 使用RBF核的SVM + 网格搜索
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [0.001, 0.01, 0.1, 1]
}

grid = GridSearchCV(SVC(kernel='rbf'), param_grid, cv=5, n_jobs=-1, verbose=1)
grid.fit(X_train, y_train)

print("最佳参数:", grid.best_params_)
print("训练集准确率:", grid.best_score_)
print("测试集准确率:", grid.best_estimator_.score(X_test, y_test))

# 5️⃣ PCA降维可视化（2维展示决策边界）
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
X_train_pca, X_test_pca = train_test_split(X_pca, test_size=0.3, random_state=42, stratify=y)

best_C = grid.best_params_['C']
best_gamma = grid.best_params_['gamma']

model = SVC(kernel='rbf', C=best_C, gamma=best_gamma)
model.fit(X_train_pca, y_train)

# 生成网格坐标
x_min, x_max = X_pca[:, 0].min() - 1, X_pca[:, 0].max() + 1
y_min, y_max = X_pca[:, 1].min() - 1, X_pca[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),
                     np.linspace(y_min, y_max, 300))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 6️⃣ 绘制决策边界
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, alpha=0.2, cmap=plt.cm.coolwarm)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, s=30, edgecolors='k', cmap=plt.cm.coolwarm)
plt.title(f"SVM on Wine Dataset (RBF kernel)\nC={best_C}, γ={best_gamma}")
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.show()

三、结果说明

运行后会输出：

复制代码

最佳参数: {'C': 10, 'gamma': 0.01}
训练集准确率: ≈ 0.985
测试集准确率: ≈ 0.96

（具体数值会因随机分割略有不同）

并显示一张 PCA 投影的二维分类图：

不同颜色代表不同酒类；
背景颜色表示 SVM 的分类区域；
可以看到 RBF 核能很好地分开三类葡萄酒样本。

四、分析要点

参数	含义	对结果的影响
C	惩罚项	控制错误分类的容忍度（越大越贴合训练集）
γ	核函数参数	控制"局部影响"范围（越大越复杂）
StandardScaler	标准化	对 SVM 至关重要，防止特征尺度失衡
PCA	可视化手段	仅用于二维展示，不影响真实模型性能

练习题

把核函数改为 'linear' 和 'poly' 进行对比；

文章目录

SVM 简介

一、基本原理

二、SVM 的主要特点

三、应用场景

四、简单例子（Python）

SVM参数

一、SVM 的核心参数（SVC() ）

二、参数详解

三、常见核函数比较

四、常见调参策略

五、调参经验总结

网格搜索

一、核心调参逻辑

二、网格搜索（GridSearchCV）

1. 基本思想

📜 2. 代码示例

三、调参结果可视化

四、经验法则（实战调参技巧）

五、实战建议

理解

一、可视化目标

二、完整 Python 示例代码

三、结果解读

四、经验总结

五、可视化结论

另一个数据

一、示例目标

二、完整可运行代码示例

三、运行效果说明

四、核心观察结论

五、进一步实验建议

{'C': 1, 'gamma': 0.1}

练习题

一、数据简介

二、Python 实例代码（含参数调优 + 可视化）

三、结果说明

四、分析要点

练习题

一、SVM 的核心参数（`SVC()` ）