【数据结构与算法】手撕排序算法(二)
一.前情回顾

上篇文章详细介绍了插入排序和选择排序两大排序算法,简单回顾一下:
1.直接插入排序:
核心思想:
"打扑克理牌过程",从前往后将未排序区间的数与已排序区间的数进行比较,插入到有序区间中。
过程:
①将第一个数认为已经有序。
②将待排序区间的数字与有序区间的数进行比较。
③比有序区间的数小,继续往前比较,直到遇到比其大的数,插入到当前位置。
④依次让待排序区间的数进行此操作,直到所有数都已排完序。
2.希尔排序
核心思想:
直接插入排序的改进版,通过增加gap,将数组分为若干个以gap为间隔的子序列,分别对子序列进行直接插入排序,逐步缩小gap,最后当gap为1时,数组实现基本有序,再对数组整体进行直接插入排序。
过程:
①选择一个增量序列gap,gap=n/2,n/4...。
②对间隔为gap的子序列内部进行直接插入排序。
③缩小gap,重复步骤②。
④gap=1时,数组实现基本有序,对数组整体进行直接插入排序。
3.直接选择排序
核心思想:
"打擂台",每次从未排序的序列里挑选出最大的或者最小的元素,与未排序的第一个元素交换位置,直至所有元素排好序。
过程:
①在未排序的序列里遍历找到最小的值。
②将其与未排序的序列的第一个元素交换位置。
③已排序序列加一,未排序的序列个数减少一。
④对剩下未排序的序列重复该步骤,直至所有元素排好序。
4.堆排序
核心思想:
直接选择排序的改进版,通过堆这种数据结构来实现选择最大(最小)元素的过程。
过程(以升序排序为例):
①建堆:将待排序列构建一个大顶堆(父节点>=子节点),此时根节点为所有节点中的最大值。
②交换:将堆顶元素(根节点,即最大值)与堆末尾元素交换,此时最大值就在序列最末尾。
③重新建堆:将剩余元素重新构建成一个大顶堆,此时的堆顶元素就是次大值。
④再次交换:再将此时的堆顶元素与堆末尾元素交换,次大元素就在序列倒数第二的位置。
⑤重复:重复③④操作,直到所有堆中只剩一个元素。
二.交换排序
1.冒泡排序
冒泡排序是最简单的一种排序算法,核心思想就是从前往后两两比较相邻的元素,逆序就交换位置,顺序则继续往后比较,直到所有元素有序。
以【6,3,5,1】数组为例
第一趟比较:
①比较6和3,两数逆序,交换位置,数组变成【3,6,5,1】。
②比较6和5,两数逆序,交换位置,数组变成【3,5,6,1】。
③比较6和1,两数逆序,交换位置,数组变成【3,5,1,6】。
第二趟比较:
①比较3和5,两数顺序,继续往后比较。
②比较5和1,两数逆序,交换位置,数组变成【3,1,5,6】。
③比较5和6,两数顺序,继续下一趟比较。
第三趟比较:
①比较3和1,两数逆序,交换位置,数组变成【1,3,5,6】。
②比较3和5,两数顺序,继续往后比较。
③比较5和6,两数顺序,比较完成,数组完成排序。
视频演示如图:
冒泡排序演示视频(来源于B站博主@蓝不过海呀
算法实现:
//冒泡排序
void BubbleSort(int* arr, int size)
{
//记录数组是否有序
int flag = 0;
for (int i = 0; i < size; i++)
{
for (int j = i + 1; j < size - 1; j++)
{
if (arr[j] < arr[i])
{
flag = 1; //进入该条件说明存在逆序,则初始数组不是全部有序的
Swap(&arr[j], &arr[i]);
}
}
//若一趟排序后flag未被修改,说明初始数组全部有序,则直接break返回
if (flag == 0)
break;
}
}冒泡排序时间复杂度:
最好情况:O(n),平均情况:O(n2),最坏情况:O(n2)
因为在交换过程中,两个相同的数的相对顺序并不会改变,所以冒泡排序是稳定的排序。
2.快速排序
快速排序就是我们常说的快排,快排的核心思想分区和原地排序。
第一步:
通过每趟排序挑出一个枢轴(关键字),将其余元素与该枢轴(关键字)比较,定义一个左右指针,分别指向数组最左边和最右边的位置,比它小的放到数组左边;比它大的放到数组右边;这样一趟比较下来,左边数据均小于枢轴,右边数据均大于该枢轴。
第二步:
通过继续递归排序左右区间,继续选出新的枢轴,继续将数组通过比较交换,将数组划分为左区间均小于枢轴,右区间均大于枢轴。
第三步:
重复递归直到区间只有一个元素,此时数组天然有序,直接返回,此时数组已经有序。
可以先通过一个用辅助数组完成排序的视频来理解以下快排的思想:
快排辅助数组版
但是辅助数组空间复杂度为O(N),消耗较大,所以实际应用中都是使用指针进行原地排序,下面来详细介绍一下(以数组【7,4,9,2,1,8,6,3】为例)。
①首先选出一个数作为枢轴,这里选择数组第一个数7作为pivot(枢轴),定义左右指针,分别指向递归区间的最左和最右。
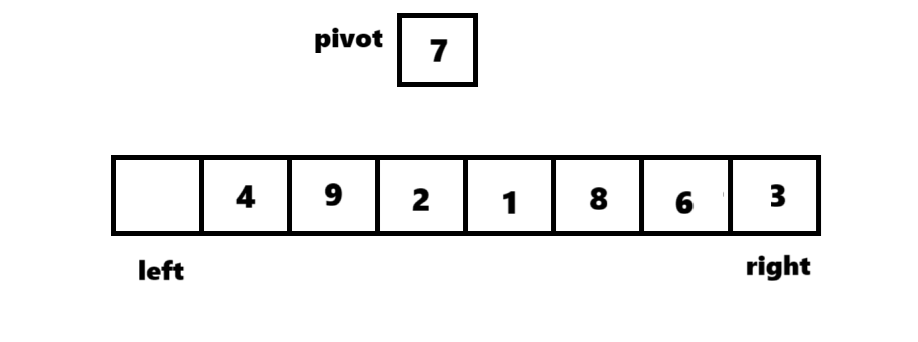
②先让arr[right]数据与pivot进行比较,若大于pivot则right--,继续比较;若小于pivot则将数据放到arr[left]里。
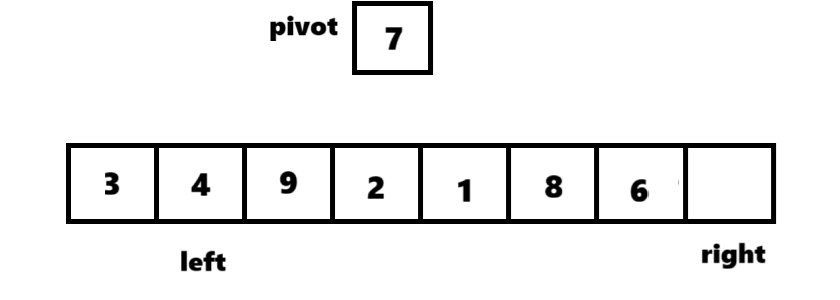
③若指针里的数据进行了交换,则换另一个指针继续比较。此时arr[left]小于pivot,left++,继续往后比较,此时arr[left]大于pivot,与arr[right]交换。 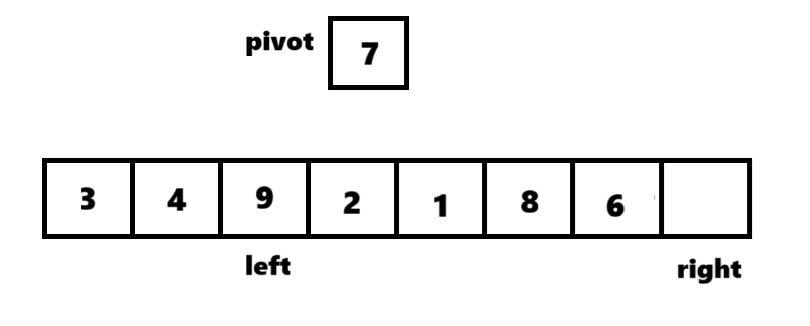
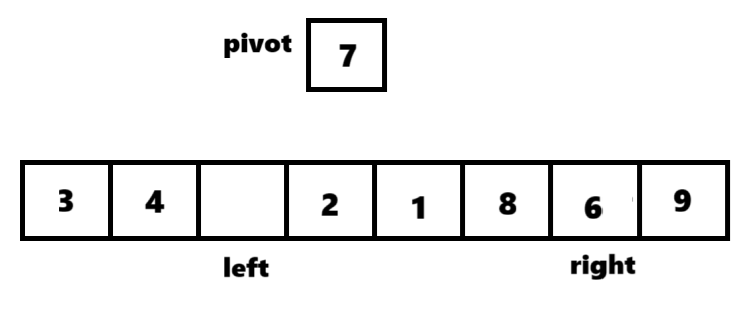
④重复②③操作,直到左区间均小于pivot,右区间均大于pivot。
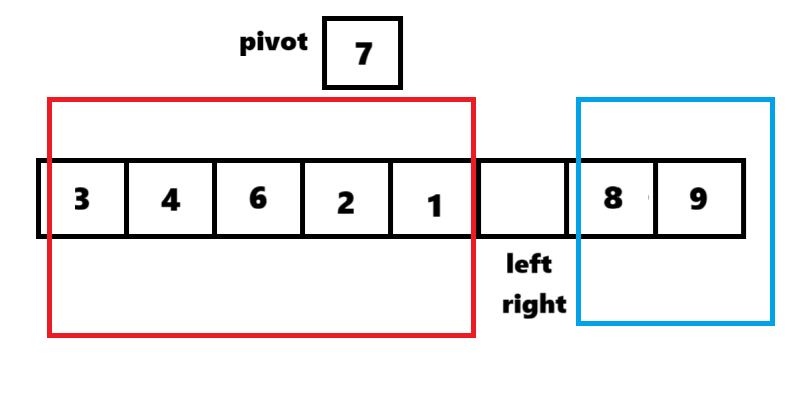
此时arr[left](或arr[right])就是pivot应在的位置。
⑤继续递归左右区间,直到最后区间只剩一个元素,递归完成,数组有序。
该方法就是选出一个基准值(pivot),将其位置视为一个"坑",然后左右指针往中间扫描,遇到合适的数据就"填坑",并在原地留下一个新的"坑",继续扫描数组,最终留下的'坑'的位置就是基准值的位置。因此该方法也被称为"挖坑法"。
算法实现为:
cpp
//快排
void QuickSort(int* arr, int begin,int end)
{
//递归出口
if (begin >= end)
return;
int left = begin, right = end;
int pivot = arr[left]; //选择第一个数据为基准值,0下标的位置即为坑
while (left < right)
{
//内部循环可能会出现left==right的情况,所以内部也需要判断
while (left < right&&arr[right] >= pivot)
{
right--;
}
//走到这里说明此时arr[right]的数据小于pivot,填坑
arr[left] = arr[right];
while (left < right&&arr[left] <= pivot)
{
left++;
}
//走到这里说明此时arr[left]的数据大于pivot,填坑
arr[right] = arr[left];
}
//left等于right时,此时的位置就是pivot的位置
//left等于right时,此时的位置就是pivot的位置
arr[left] = pivot;
//左区间为[begin,left-1]
QuickSort(arr, begin, left - 1); //递归左区间
//[right+1,end]
QuickSort(arr, right + 1, end); //递归右区间
}视频演示:
快排
三.归并排序(递归版)
归并排序的核心思想就是分治,通过递归将数组每次对半分为子数组,再将子数组也对半分为两个子数组,直到子数组元素个数为1(此时数组天然有序),然后再将它们合并起来,最后合并成一个有序数组。
分治:分而治之,就是将原本复杂庞大的问题拆解成若干个规模更小,结构相同的小问题,递归地解决这些小问题,将小问题的解合并即得到原来大问题的解。
例如你要统计一个学校的所有学生人数,你不会一个一个去数,而是会让每个班级上报人数,你再把各个班级的人数加起来。这里,"统计全校人数"是大问题,"统计每个班级人数"就是子问题。
以【56,23,41,76,18,69,57,18,26,43,15】为例:
第一步:分解(递归将数组对半分成子数组)
数组长度为11,mid
归并排序
算法实现如下:
cpp
//归并排序(凡是递归,参数都得是左右区间)
void _MergeSort(int* arr, int left, int right, int* tmp)
{
if (left == right)
return;
int mid = (left + right) >> 1;//右移相当于除2
//[left,mid] [mid+1,right]
_MergeSort(arr, left, mid, tmp);//递归左区间
_MergeSort(arr, mid+1, right, tmp);//递归右区间
//归并
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
tmp[index++] = arr[begin1++];
else
tmp[index++] = arr[begin2++];
}
while (begin1 <= end1)
tmp[index++] = arr[begin1++];
while (begin2 <= end2)
tmp[index++] = arr[begin2++];
//拷贝
for (int i = left; i <= right; i++)
arr[i] = tmp[i];
}
void MergeSort(int* arr, int n)
{
//辅助数组,保存归并后的数据
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(arr, 0, n - 1,tmp);
free(tmp);
}四.总结
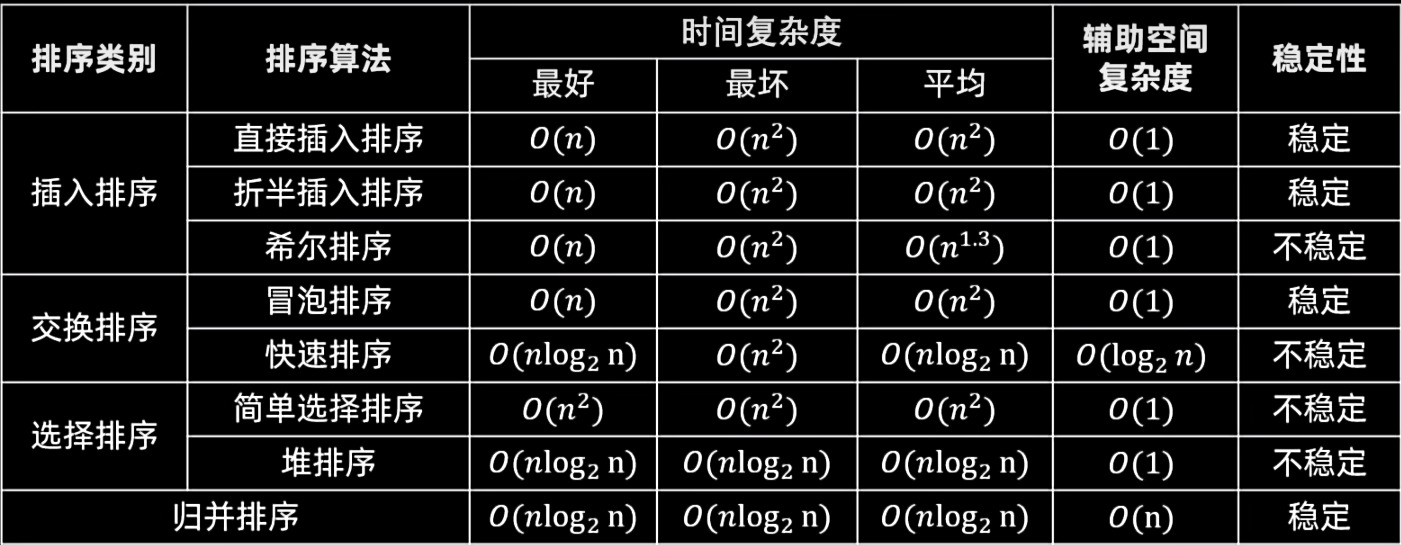
事实上目前没有出现十全十美的一种排序算法,每种算法都既有优点也有缺点,即使是快排,也存在着辅助空间大,不稳定的缺点。因此就从多个角度比较以下各个排序算法的长与短。
感谢阅读 ^ _ ^