Leetcode 46

im_AMBER2025-11-07 20:59

1 题目

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

复制代码 
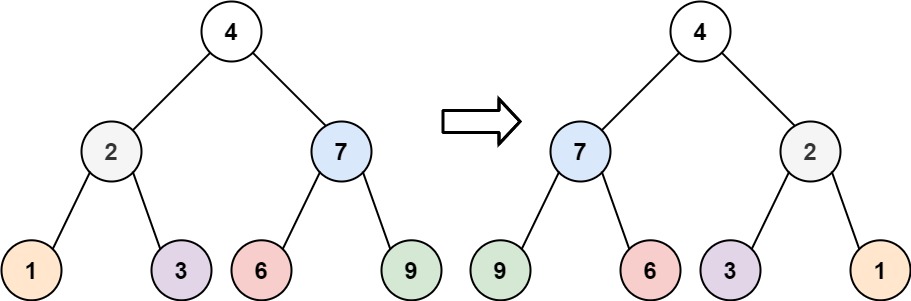
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

复制代码 
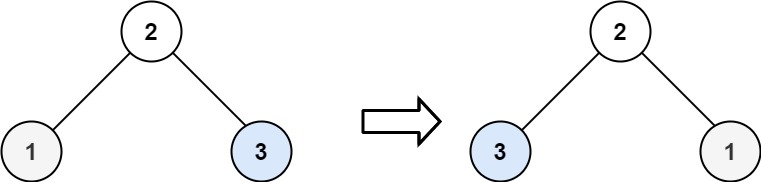
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

复制代码 
输入：root = []
输出：[]

提示：

  • 树中节点数目范围在 [0, 100] 内
  • -100 <= Node.val <= 100

2 代码实现

分解

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
typedef struct TreeNode TreeNode;
struct TreeNode* invertTree(struct TreeNode* root) {
    if (root == NULL ){
        return NULL;
    }
    TreeNode* left = invertTree(root -> left);
    TreeNode* right = invertTree(root -> right);

    root -> left = right;
    root -> right = left;

    return root;
}

递归思想，完整读了笔记以后感觉没很难。之前也做过。这里想到的是分解的做法。

遍历

cpp 复制代码 
class Solution {
public:
    // 主函数
    TreeNode* invertTree(TreeNode* root) {
        // 遍历二叉树，交换每个节点的子节点
        if(root != NULL) traverse(root);
        return root;
    }

    // 二叉树遍历函数
    void traverse(TreeNode* root) {
        if(root != NULL) {
            // *** 前序位置 ***
            // 每一个节点需要做的事就是交换它的左右子节点
            TreeNode* tmp = root->left;
            root->left = root->right;
            root->right = tmp;

            // 遍历框架，去遍历左右子树的节点
            traverse(root->left);
            traverse(root->right);
        }
    }
};

二叉树心法（思路篇） | labuladong 的算法笔记https://labuladong.online/algo/data-structure/binary-tree-part1/#%E7%AC%AC%E4%B8%80%E9%A2%98%E3%80%81%E7%BF%BB%E8%BD%AC%E4%BA%8C%E5%8F%89%E6%A0%91

用c实现

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
typedef struct TreeNode TreeNode;
struct TreeNode* invertTree(struct TreeNode* root) {
    if (root == NULL ){
        return NULL;
    }

    TreeNode * temp = root -> left;
    root -> left = root -> right;
    root -> right = temp;

    TreeNode* left = invertTree(root -> left);
    TreeNode* right = invertTree(root -> right);

    return root;
}

3 题目

116. 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

复制代码 
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

复制代码 
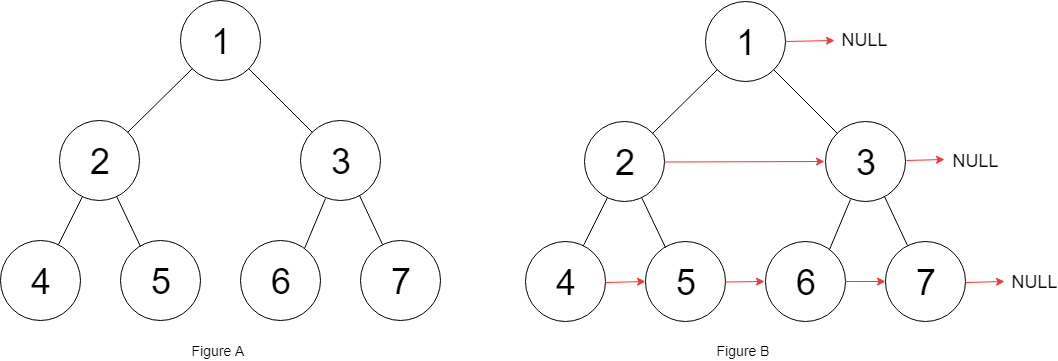
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

复制代码 
输入：root = []
输出：[]

提示：

  • 树中节点的数量在 [0, 212 - 1] 范围内
  • -1000 <= node.val <= 1000

进阶：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

4 代码实现

cpp 复制代码 
/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *left;
 *     struct Node *right;
 *     struct Node *next;
 * };
 */
typedef struct Node Node;
void traverse(Node* node1 , Node* node2){
   if(node1 == NULL || node2 == NULL){
    return;
   }    
        node1 -> next = node2 ;

        traverse(node1 -> left , node1 -> right);
        traverse(node2 -> left , node2 -> right);
        traverse(node1 -> right , node2 -> left);
    }

struct Node* connect(struct Node* root) {
	if(root == NULL){
        return NULL ;
    }
    traverse(root -> left ,root -> right);
    return root;
}

结合算法笔记和题解豁然开朗了，二叉树没有那么可怕。

二叉树心法（思路篇） | labuladong 的算法笔记

cpp 复制代码 
class Solution {
public:
    // 主函数
    Node* connect(Node* root) {
        if (root == nullptr) return nullptr;
        // 遍历「三叉树」，连接相邻节点
        traverse(root->left, root->right);
        return root;
    }

    // 三叉树遍历框架
    void traverse(Node* node1, Node* node2) {
        if (node1 == nullptr || node2 == nullptr) {
            return;
        }
        // *** 前序位置 ***
        // 将传入的两个节点穿起来
        node1->next = node2;
        
        // 连接相同父节点的两个子节点
        traverse(node1->left, node1->right);
        traverse(node2->left, node2->right);
        // 连接跨越父节点的两个子节点
        traverse(node1->right, node2->left);
    }
};

这段代码是用于解决「填充每个二叉树节点的右侧指针」问题的，核心思路是通过一种类似「三叉树遍历」的方式，把二叉树中同一层的节点用 next 指针连接起来。下面我会用非常详细的方式解释每一步，确保你能理解。

先明确问题：什么是「填充右侧指针」？

假设我们有一棵完美二叉树 （每个节点要么有 0 个孩子，要么有 2 个孩子，且同一层节点齐全），每个节点除了 left（左孩子）、right（右孩子），还有一个 next 指针。要求是：将同一层的所有节点通过 next 指针连接起来，每个节点的 next 指向它右侧的节点；如果右侧没有节点，next 为 null。

例如，一棵 3 层的完美二叉树：

bash 复制代码 
        1
      /   \
     2     3
    / \   / \
   4   5 6   7

填充后，next 指针的指向应该是：2->3，4->5，5->6，6->7，且 3、7 的 next 为 null。

代码核心思路：把二叉树当「三叉树」遍历

常规的二叉树遍历（前序、中序、后序）只关注单个节点和它的左右孩子。但这里要连接同一层的相邻节点 ，这些节点可能来自不同的父节点（比如 5 和 6，它们的父节点分别是 2 和 3）。

所以代码的巧妙之处在于：不局限于单个节点的左右孩子，而是同时处理两个相邻的节点，通过递归让它们的子节点也互相连接。这就像把两个相邻节点和它们的子节点组成了一棵「三叉树」，从而能处理跨父节点的连接。

逐行解释代码

1. 主函数 connect(Node* root)
cpp 复制代码 
if (root == nullptr) return nullptr;
// 遍历「三叉树」，连接相邻节点
traverse(root->left, root->right);
return root;
  • 作用：处理整个树的入口。
  • 第一步：如果根节点为空，直接返回（空树无需处理）。
  • 第二步：调用 traverse 函数，传入根节点的左孩子和右孩子（因为根节点是第一层，它的 next 为 null，无需处理；从第二层的 root->left 和 root->right 开始连接）。
  • 最后返回处理完的根节点。
2. 核心函数 traverse(Node* node1, Node* node2)

这个函数是关键，它的参数是两个相邻的节点 （node1 在左，node2 在右），作用是：

  1. 把 node1 的 next 指向 node2（直接连接这两个节点）。
  2. 递归处理 node1 的左右孩子（同一父节点的相邻节点）。
  3. 递归处理 node2 的左右孩子（同一父节点的相邻节点）。
  4. 递归处理 node1 的右孩子和 node2 的左孩子（跨父节点的相邻节点）。
第一步：终止条件
cpp 复制代码 
if (node1 == nullptr || node2 == nullptr) {
    return;
}
  • 如果两个节点中有一个为空，就无需处理（因为 next 指针默认是 null）。
第二步：前序位置 - 连接当前两个节点
cpp 复制代码 
// *** 前序位置 ***
// 将传入的两个节点穿起来
node1->next = node2;
  • 「前序位置」指的是在处理子节点之前，先处理当前节点。这里的「当前节点」就是 node1 和 node2 这一对相邻节点。
  • 直接让 node1 的 next 指向 node2，完成它们的连接。
第三步：连接同一父节点的子节点
cpp 复制代码 
// 连接相同父节点的两个子节点
traverse(node1->left, node1->right);
traverse(node2->left, node2->right);
  • 对于 node1 来说，它的左孩子和右孩子是同一父节点的相邻节点，需要连接（比如 node1 是 2，则连接 4 和 5）。
  • 同理，node2 的左孩子和右孩子也需要连接（比如 node2 是 3，则连接 6 和 7）。
第四步：连接跨父节点的子节点
cpp 复制代码 
// 连接跨越父节点的两个子节点
traverse(node1->right, node2->left);
  • 这是最关键的一步！node1 的右孩子和 node2 的左孩子虽然来自不同的父节点，但它们在同一层且相邻（比如 node1 是 2，node2 是 3，则 5 和 6 需要连接）。
  • 通过递归处理这两个节点，让它们也通过 next 连接起来。

用例子模拟整个过程

以开头的 3 层树为例，模拟 traverse 函数的调用过程：

  1. 主函数调用 traverse(2, 3)（根节点 1 的左右孩子）。
    • 前序位置：2->next = 3（完成 2 和 3 的连接）。
    • 递归 1：traverse(2->left, 2->right) → traverse(4,5)。
      • 前序：4->next=5。
      • 递归 traverse(4->left,4->right)（都是 null，返回）。
      • 递归 traverse(5->left,5->right)（都是 null，返回）。
      • 递归 traverse(4->right,5->left)（都是 null，返回）。
    • 递归 2：traverse(3->left,3->right) → traverse(6,7)。
      • 前序：6->next=7。
      • 后续递归都是 null，返回。
    • 递归 3：traverse(2->right,3->left) → traverse(5,6)。
      • 前序：5->next=6（完成跨父节点的连接）。
      • 后续递归都是 null，返回。

最终所有同一层的节点都被 next 连接起来，结果符合要求。

总结

  • 核心思想：通过 traverse 函数同时处理两个相邻节点，不仅连接它们本身，还递归连接它们的子节点（包括同一父节点和跨父节点的情况）。
  • 为什么叫「三叉树遍历」？因为每个 traverse 调用会处理两个节点，再衍生出三个递归调用（左孩子对、右孩子对、跨父节点对），类似三叉树的结构。
  • 优势：时间复杂度是 O(n)（每个节点被处理一次），空间复杂度是 O(h)（递归栈深度，h 是树的高度），非常高效。
相关推荐
charlie1145141911 小时前
从零开始理解 CSS：让网页“活”起来的语言2
前端·css·笔记·学习·选择器·样式表·原生
QX_hao2 小时前
【Go】--文件和目录的操作
开发语言·c++·golang
卡提西亚2 小时前
C++笔记-20-对象特性
开发语言·c++·笔记
努力学算法的蒟蒻2 小时前
day09（11.6）——leetcode面试经典150
算法·leetcode·职场和发展
2301_796512522 小时前
Rust编程学习 - 内存分配机制，如何动态大小类型和 `Sized` trait
学习·算法·rust
三掌柜6663 小时前
C++ 零基础入门与冒泡排序深度实现
java·开发语言·c++
秦明月133 小时前
EPLAN电气设计：快捷键版本差异解析
经验分享·学习·学习方法·设计规范
卿言卿语3 小时前
CC23-最长的连续元素序列长度
java·算法·哈希算法
沐怡旸3 小时前
【穿越Effective C++】条款15：在资源管理类中提供对原始资源的访问——封装与兼容性的平衡艺术
c++·面试
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06npm使用国内淘宝镜像的方法07《大数据技术原理与应用》实验报告三 熟悉HBase常用操作08BongoCat - 跨平台键盘猫动画工具09NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南10jdk21下载、安装（Windows、Linux、macOS）