Java基础——常用算法4

lkbhua莱克瓦242025-11-08 8:45

一、排序算法

1.1 插入算法

🌟 一、什么是插入排序？

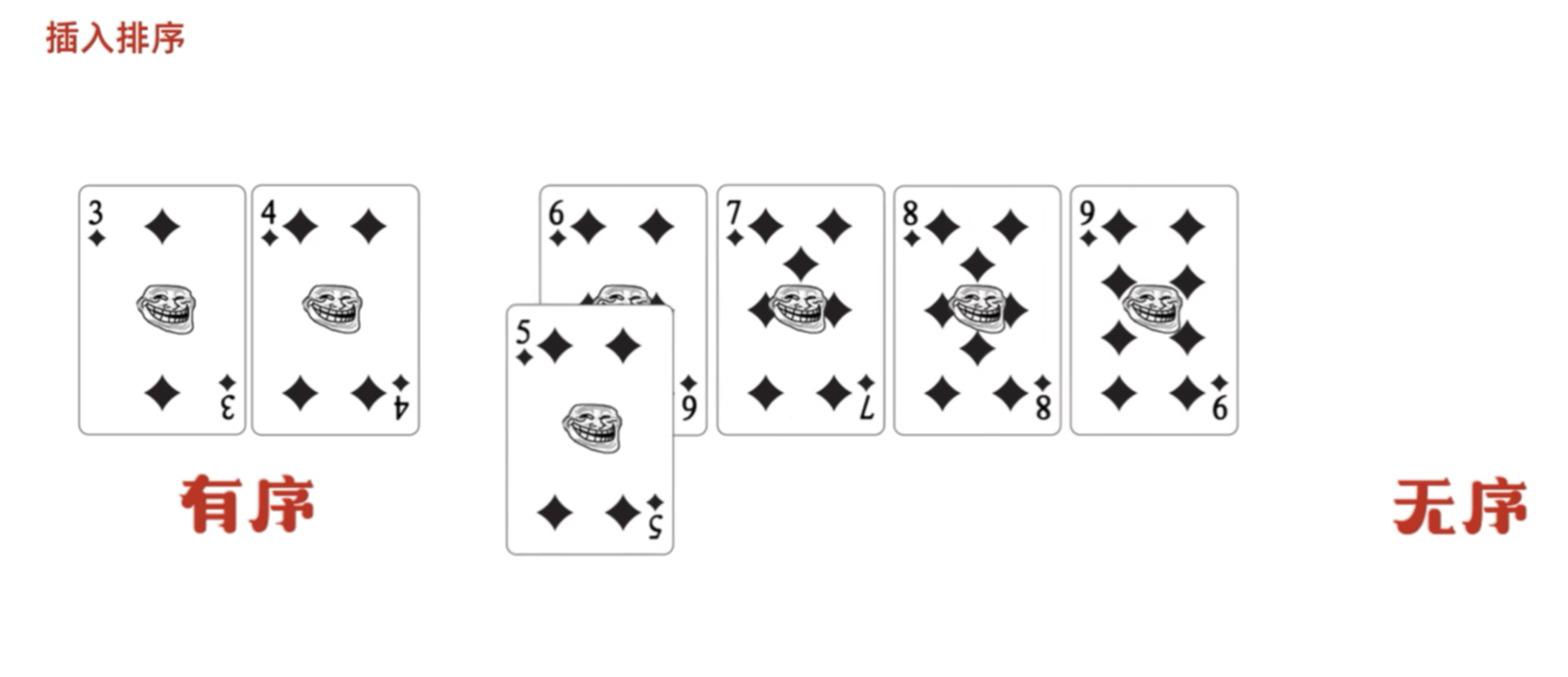
插入排序（Insertion Sort） 是一种简单、直观且高效的比较类排序算法，其思想来源于我们打扑克牌时整理手牌的方式：

每次从未排序部分取出一个元素，插入到已排序部分的正确位置。

名字来源：像"插入"一张新牌到已有有序序列中。

🔁 二、插入排序的工作原理

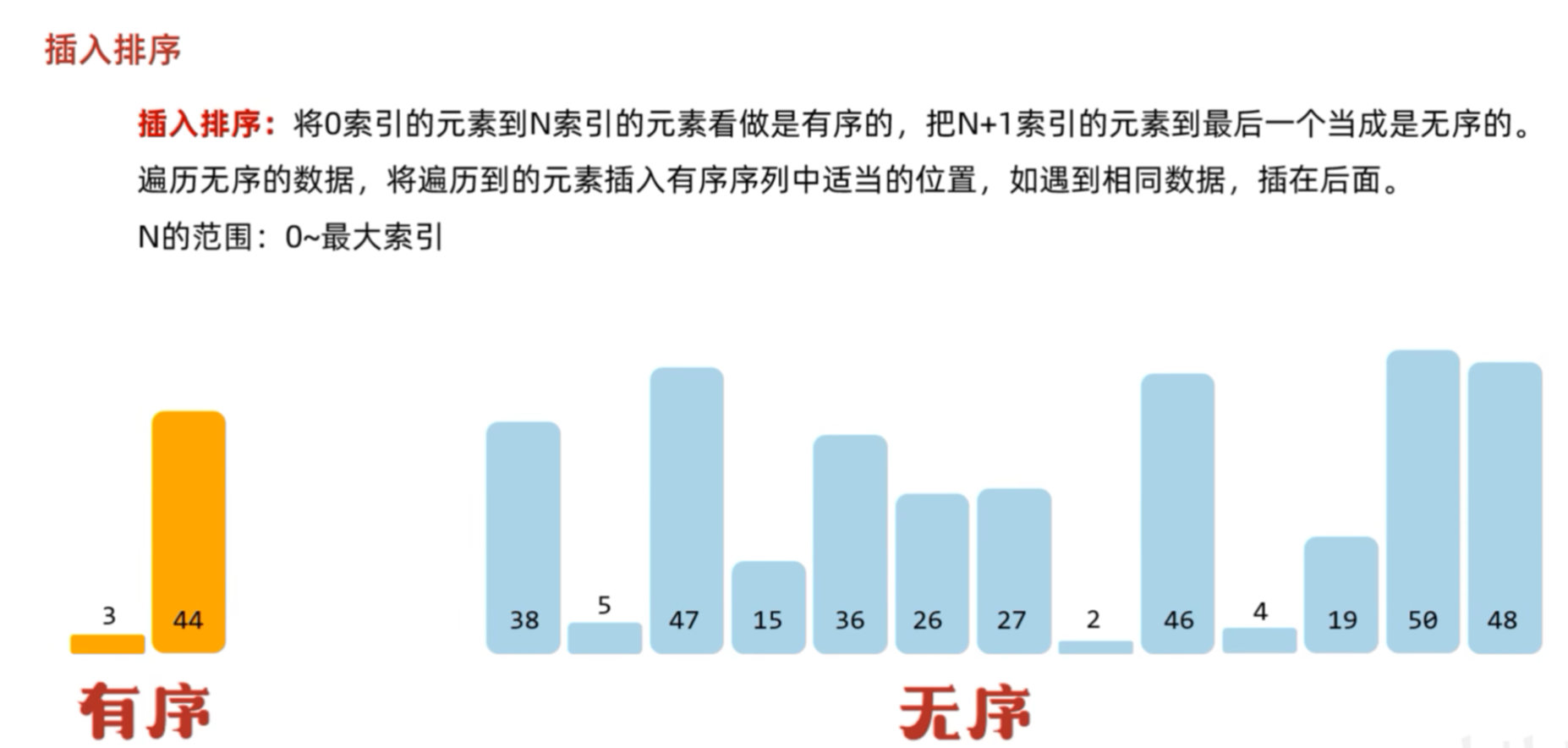
如果数据比较乱，我们默认第一张或者第一个元素的数据就是有序的，其他的都看作无序的。

再从遍历无序的数组，一一跟有序的进行从后面依次进行的比较，然后插入其中。直接完成插入排序。

💻 三、Java 基础版插入排序代码实现

java 复制代码 
package com.lkbhua.Algorithm.sort;

public class InsertDemo {
    public static void main(String[] args) {
        /*插入排序：
                将0索引元素到N索引的元素看做是有序的，把N+1索引的元素到最后一个当成是无序的。
                遍历无序的数据，将遍历到的元素插入有序序列中适当的位置，如遇到相同数据，插在后面。'
                N的范围：0~最大索引*/

        int[] arr = {3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};

        // 1、规定无序的数据的范围从X开始
        int startIndex = -1 ;
        for(int i = 0; i < arr.length; i++){
            if(arr[i]> arr[i+1]){
                System.out.println(i); // 1
                // 这样就通过代码的方式找到了无序数据的开始索引
                startIndex = i + 1;
                break;
                // 这就能表示有序的那一组数组的最后一个索引
            }
        }
        // 剩下的数组就是无序的

        System.out.println("无序数据的开始索引：" + startIndex);
        // 2、遍历从startIndex开始无序的数组中的元素
        for(int i = startIndex; i < arr.length; i++){
            System.out.print(arr[i]+" ");
        }
        System.out.println();

        // 3、如何插入排序呢？
        for(int i = startIndex; i < arr.length; i++){
            // 记录当前要插入数据的索引 ,其实就是i
            // 用另外的变量记录一下
            int j = i;
            while( j > 0 && arr[j] < arr[j-1]){
                // 交换位置
                int temp = arr[j];
                arr[j] = arr[j-1];
                arr[j-1] = temp;
                j--;
            }
            // 修改这个索引
        }


        // 4、打印结果
        System.out.println("排序后：");
        for(int i = 0; i < arr.length; i++){
            System.out.print(arr[i]+" ");
        }

    }
}

📊 四、时间复杂度与空间复杂度分析

情况 时间复杂度 说明
最好情况 O(n) 数组已有序，内层循环不执行
平均情况 O(n²) 随机数据，平均移动 n/2 次
最坏情况 O(n²) 数组逆序（如 [5,4,3,2,1]），每次都要移动全部已排序元素

| 空间复杂度 | O(1) | 仅使用常量额外空间（原地排序） |

💡 插入排序是少数能在最好情况下达到 O(n) 的 O(n²) 排序算法！

🔍 五、稳定性分析

插入排序是 ✅ 稳定的排序算法。

为什么？

  • 在比较时使用 arr[j] > key（不是 >=）
  • 相等元素不会发生交换或移动，相对顺序保持不变

✅ 六、插入排序的优点

  1. 实现简单：逻辑贴近人类直觉（如理牌）
  2. 原地排序：空间复杂度 O(1)
  3. 稳定：保持相等元素顺序
  4. 在线算法：可以边接收数据边排序
  5. 对小规模或近有序数据极高效
    • 最好情况 O(n)
    • 实际运行常数小，比快排在小数据上更快

🌟 最关键优势 ：
Java 的 Arrays.sort() 在底层对小数组（长度 ≤ 47）会自动切换为插入排序！

🔗 为什么 Java 的 Arrays.sort() 会用插入排序？

这是工程实践中的经典优化！

  • 快排、归并在小数组上递归开销大
  • 插入排序在 n ≤ 10~50 时实际运行更快

插入排序虽"简单"，但它是高性能排序库的重要组成部分！

❌ 七、插入排序的缺点

  1. 时间复杂度高：O(n²)，不适合大数据量
  2. 频繁移动元素：相比选择排序（只交换），插入排序需要多次赋值
  3. 缓存性能一般：内层循环反向遍历，局部性不如顺序访问

🔍 八、入排序 vs 冒泡排序 vs 选择排序

特性 插入排序 冒泡排序 选择排序
时间复杂度（最好） O(n) O(n)（优化后） O(n²)
时间复杂度（平均） O(n²) O(n²) O(n²)
稳定性 ✅ 稳定 ✅ 稳定 ❌ 不稳定
交换/移动次数 O(n²) 次移动 O(n²) 次交换 O(n) 次交换
适用场景 小数据、近有序 教学 写操作昂贵
实际应用 ✅ 被 JDK 采用 ❌ 无 ❌ 无

💡 插入排序是三者中最实用的！

1.2 快速排序

🌟一、 递归思想

复习推文推荐：

https://blog.csdn.net/2401_84643729/article/details/154534984

🌟二、什么是快速排序？

快速排序（Quick Sort） 是由 Tony Hoare 在 1960 年提出的一种高效、原地、分治型比较排序算法 。

它是目前实际应用中最广泛使用的排序算法之一 ，也是 Java Arrays.sort() 对基本类型数组的底层实现基础。

核心思想 ：
"分而治之" + "分区（Partition）"

  1. 选择一个元素作为 基准（pivot）
  2. 将数组划分为两部分：
    • 左边：≤ pivot 的元素
    • 右边：≥ pivot 的元素
  3. 递归地对左右两部分排序

🔁 三、快速排序的工作原理

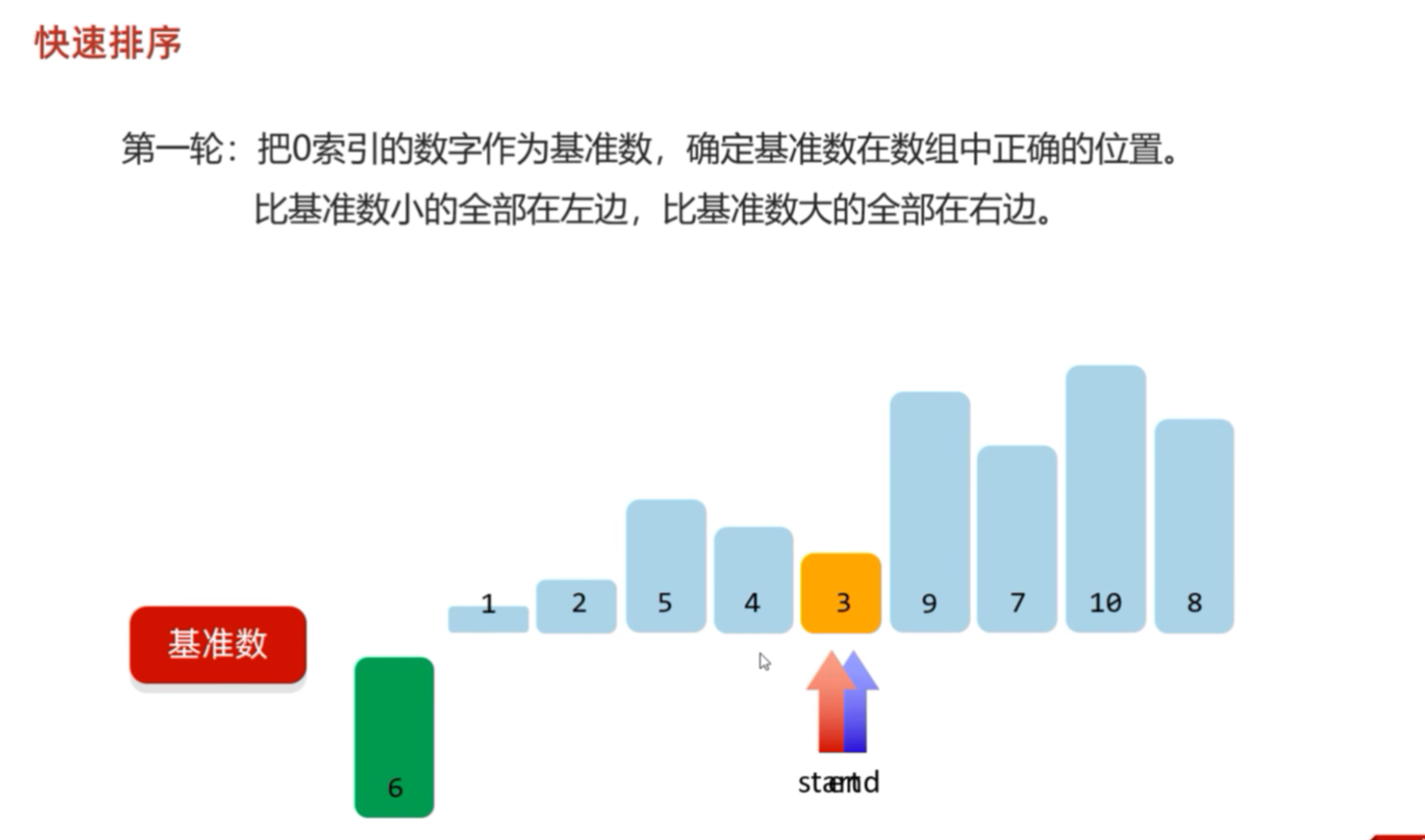
首先把0索引对应的元素6拿出来当作"基准数"，然后定义两个变量start和end用以记录头和尾。

随后移动end，让其与基准数进行比较，发现比基准数大，则不进行放置处理。让end进行--进行下一个数字判断，10也是，第三5比基准数小，end就停在这。接下来移动start，同理，一直找到第三个元素7，停止。最后拿着start指向的7和end指向的5进行交换，随后继续寻找start++，end--，4和9进行交换，直到start == end ；这个位置就是基准数存入的位置。拿着3和6进行交换，我们称之为基准数归位。至此第一轮结束。

💻 四、Java 基础版快速排序代码实现

java 复制代码 
package com.lkbhua.Algorithm.sort;

public class QuickSortDemo2 {
    public static void main(String[] args) {
        /*快速排序：完整代码
             第一轮：以0索引的数字为基准数，确定基准数在数组中正确的位置
             比基准数小的全都在左边，比基准数大的全都在右边。
             后面依次类推*/

        int[] arr = {6,1,2,7,9,3,4,5,10,8};
        quickSort(arr, 0, arr.length - 1);

        for(int i = 0; i < arr.length; i++){
            System.out.print(arr[i]+" ");
        }

    }

    // 参数一：数组
    // 参数二：左边索引
    // 参数三：右边索引
    public static void quickSort(int[] arr, int left, int right){

        // 递归的出口
        if(left >= right){
            return;
        }

        // 定义两个变量记录左右索引
        int start = left;
        int end = right;

        // 记录基准数
        int baseNumber = arr[left];

        // 利用循环找到要交换的数字
        while(start != end){
            // 利用end索引向左移动，找到比baseNumber小的数字
            while (true){
                if(end <= start || arr[end] < baseNumber){
                    break;
                }
                end--;
            }

            // 利用start索引向右移动，找到比baseNumber大的数字
            while( true){
                if(end <= start || arr[start] > baseNumber){
                    break;
                }
                start++;
            }

            // 把end和start索引的数字交换
            int temp = arr[start];
            arr[start] = arr[end];
            arr[end] = temp;

        }

        // 当start和end相等的时候，交换start索引的数字和baseNumber
        // 表示基准数在数组中的正确位置
        // 基准数归位:
        int temp = arr[left];
        arr[left] = arr[start];
        arr[start] = temp;

        // 确定6左边的范围，重复刚刚的动作
        quickSort(arr, left, start - 1);


        // 确定6右边的范围，重复刚刚的动作
        quickSort(arr, start + 1, right);

    }
}

🔍五、稳定性与原地性

特性 结论 说明
原地排序 ✅ 是 仅使用 O(1) 额外空间（不计递归栈）
稳定性 ❌ 不稳定 分区过程中相等元素可能被交换顺序

1.3 面经

📘 面试加分问题

Q1：插入排序和冒泡排序哪个更快？

A：通常插入排序更快。因为：

  • 插入排序内层是移动（赋值），冒泡是交换（三次赋值）
  • 插入排序对近有序数据更敏感，实际比较次数更少

Q2：插入排序能用于链表吗？

A：✅ 非常适合！

链表插入只需修改指针，无需移动元素，时间复杂度仍为 O(n²)，但常数更小。

Q3：为什么插入排序是稳定的？

A：因为比较条件是 > 而非 >=，相等元素不会被移动，相对顺序不变。

✅ 结语

插入排序看似简单，却是理论与实践结合的典范：

  • 教学上：帮助理解"构建有序序列"的思想
  • 工程上：被 Java、Python 等主流语言的排序库采用

🌟 记住 ：
"简单不等于无用，插入排序是高性能排序的基石之一。"

Q1：快排最坏时间复杂度是什么？如何避免？

A：最坏 O(n²)，发生在每次 pivot 都是最值（如已排序数组）。
避免方法：随机化 pivot、三数取中、使用双轴快排。

Q2：快排是稳定的吗？能改成稳定吗？

A：默认不稳定。理论上可通过额外空间记录原始索引实现稳定，但会失去"原地"优势，一般不这么做。

Q3：为什么 Java 对基本类型用快排，对对象用归并/Timsort？

A：因为对象排序要求稳定性，而快排不稳定；基本类型无"相等顺序"概念，可用更快的快排。

Q4：快排和归并排序怎么选？

  • 要求稳定 or 内存充足 → 归并
  • 内存受限 or 追求平均速度 → 快排

1.4、四大排序算法核心特性对比表📊

原地排序（In-place Sorting） 是指：
排序过程中只使用常量级（O(1)）的额外存储空间 ，即不需要创建新的数组或大量辅助结构 ，所有操作都在原数组内部通过交换或移动完成。

❌ 非原地排序（Out-of-place）：

  • 需要额外的数组或数据结构来辅助排序
  • 空间复杂度通常为 O(n)

💡 举个例子：

复制代码 
1// 原地：直接在 arr 上操作
2bubbleSort(arr); // 排序后 arr 本身被修改
3
4// 非原地（伪代码）：
5int[] sorted = mergeSort(arr); // 返回一个新数组，原 arr 不变

✅ 关键判断标准 ：
除了输入数组外，算法是否只用了几个变量（如 temp, i, j）？如果是，就是原地排

特性 冒泡排序（Bubble Sort） 选择排序（Selection Sort） 插入排序（Insertion Sort） 快速排序（Quick Sort）
是否原地 ✅ 是 ✅ 是 ✅ 是 ✅ 是
空间复杂度 O(1) O(1) O(1) O(log n) ~ O(n) ⚠️
时间复杂度（最好） O(n)（优化后） O(n²) O(n) O(n log n)
时间复杂度（平均） O(n²) O(n²) O(n²) O(n log n)
时间复杂度（最坏） O(n²) O(n²) O(n²) O(n²)（可优化避免）
稳定性 ✅ 稳定 ❌ 不稳定 ✅ 稳定 ❌ 不稳定
交换/移动次数 最多 O(n²) 次交换 最多 n-1 次交换 最多 O(n²) 次移动 O(n log n) 次交换（平均）
适用场景 教学、极小数据 写操作昂贵的小数据 小数据、近有序数据 大数据、通用高性能排序
Java 标准库是否使用 ❌ 否 ❌ 否 ✅ 是（小数组优化） ✅ 是（基本类型主算法）

Q1：为什么快排空间复杂度是 O(log n) 而不是 O(1)？

  • 快排使用递归 ，每次递归调用都会在系统栈（call stack） 中占用空间
  • 平衡情况下，递归深度为 log n → 空间 O(log n)
  • 最坏情况下（如已排序数组），递归深度为 n → 空间 O(n)

✅ 但业界仍认为快排是"原地排序"，因为：

  • 额外空间来自递归栈，而非显式分配的数组
  • 没有使用与输入规模成正比的额外堆内存（heap）
  • 对比归并排序（明确需要 O(n) 的临时数组），快排更节省内存

Q2、总结："原地"意味着什么？

算法 是否原地 为什么？
冒泡排序 ✅ 仅用几个变量交换相邻元素
选择排序 ✅ 每轮只做一次交换，无需额外数组
插入排序 ✅ 元素右移腾位，不依赖外部空间
快速排序 ✅（广义） 无额外数组，但递归栈占用 O(log n) 空间

声明：

题目详细分析借鉴于通义AI

以上均来源于B站@ITheima的教学内容！！！

本人跟着视频内容学习，整理知识引用

相关推荐
.格子衫.2 小时前
Maven高级
java·maven
.格子衫.2 小时前
Maven前奏
java·pycharm·maven
m0_748248022 小时前
揭开 C++ vector 底层面纱：从三指针模型到手写完整实现
开发语言·c++·算法
学渣676562 小时前
11111
笔记
MeowKnight9582 小时前
【DIY】PCB练习记录2——51单片机核心板
笔记
Mos_x2 小时前
springboot系列--自动配置原理
java·后端
七夜zippoe2 小时前
Ascend C流与任务管理实战：构建高效的异步计算管道
服务器·网络·算法
神奇侠20242 小时前
基于spring-boot-admin实现对应用、数据库、nginx等监控
java·数据库·nginx
一叶飘零_sweeeet3 小时前
手写 RPC 框架
java·网络·网络协议·rpc
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06npm使用国内淘宝镜像的方法07BongoCat - 跨平台键盘猫动画工具08《大数据技术原理与应用》实验报告三 熟悉HBase常用操作09jdk21下载、安装（Windows、Linux、macOS）10NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南