【剑斩OFFER】算法的暴力美学——二分查找

一、题目描述

二、算法原理

从题目的要求我们可以看出这道题是有二段性的性质的，所谓的二段性：在一段区间内根据数据的规律可以把这个区间分为两个区间；所以我们使用二分查找算法来解决这道题：

先把这段数组的加标的中间下标求出来，然后我们就的到这样的规律：

①当 nums[ mid ] > target 时，【mid，right】区间内的数字都不可能等于 target，只有在【left，mid】区间内的数字有可能等于 target，所以我们让 right = mid - 1 ，到新的【left，right】来找：

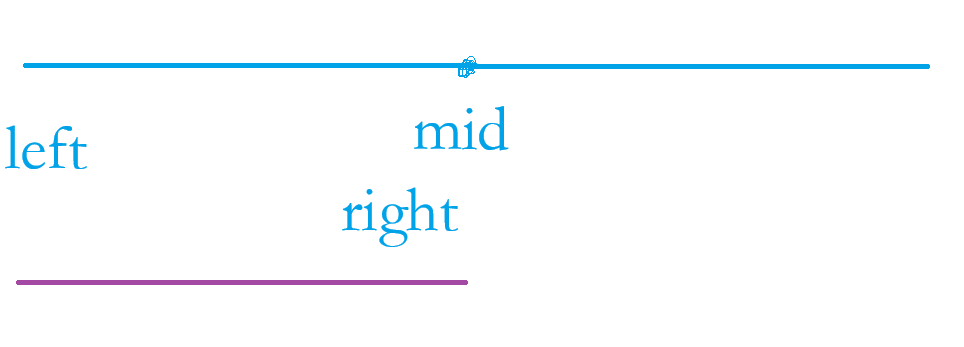
②当 nums[ mid ] < target 时，【mid，right】区间才有可能找到target；所以：left = mid + 1，到新的【left，right】来找：

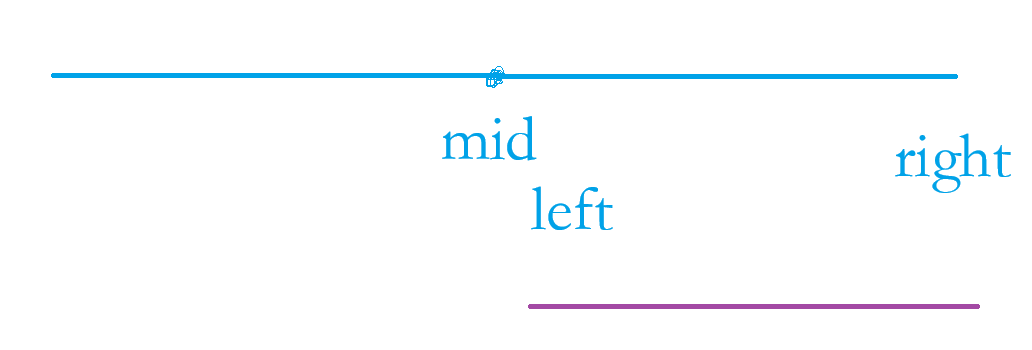
③nums[ mid ] == target时，直接返回：mid。

然后不断循环上面的①②③来找到正确答案。

细节：

循环结束的条件：当我们不断二分时有可能 left 和 right 指向同一个数，我们还要判断一下这个数是不是符合条件的数，所以我们循环的条件是：left <= right ，当 left > right 时就结束循环。

事件复杂度：

假设数组里面的数字有 n 个：

1次二分：n/2

第二次二分：n/4

第三次二分：n/8

...........

第x次二分：n/(2^x)；此时不断的二分导致这个数接近 1，所以：1 = n/(2^x) -> 2^x = n

所以时间复杂度为：O（logn)

求mid的值的方法：

①int mid = ( left+ right）/ 2，当数据量过大时 left + right 有可能超过 int 的最大值造成数据溢出，不推荐这种方法。

实例这种方法是否能求出数组下标的中间下标：

当：left = 1 ， right = 4，（left + right ）/ 2 = 2，当left + right 是一个奇数时求出的mid偏小：5/2 = 2.5 = 2。

当：left = 2，right = 4 ，（left + right）/2 = 3，当 right + left 是一个偶数是球场的数是正确的mid。

注意：求的是数组的left 和 right下标的中间下标

②int mid = left + (right - left ) / 2，这种方法推荐，防止数据溢出。

问题：为什么是二分不能是三分、四分呢？

答：因为根据数学期望得出的二分是效率最高的。

三、朴素二分模板

cpp 复制代码

        while(left <= right)
        {
            int mid =left + (right - left)/2;
            if(.......) 
                ...........;
            else if(..........) 
                ............;
            else return .........;
        }
注：.....是根据每道题目的二段性来填写

四、代码实现

cpp 复制代码

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0,right = nums.size()-1;
        while(left <= right)
        {
            int mid =left + (right - left)/2;
            if(nums[mid] > target) right = mid - 1;
            else if(nums[mid] < target) left = mid + 1;
            else return mid;
        }
        return -1;
    }
};